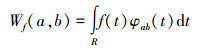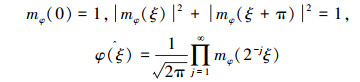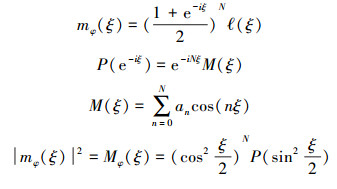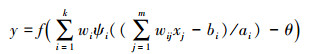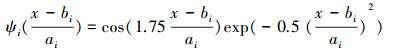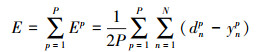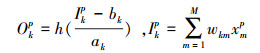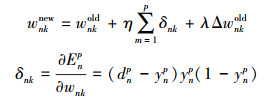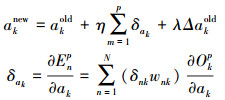轴承作为旋转机械中应用最广泛的零件之一,其工作状态对于机械设备的稳定性、使用寿命、振动及噪声等均有着关键的影响[1]。在实际生产中,轴承故障诊断的精确性与实时性对于降低机械设备的突发性中断、减少经济损失和事故有着重要的意义[2]。
目前,应用较为广泛的故障诊断技术有时域法与频域法等[3],其主要通过轴承不同损伤下的振动特性进行故障分析和预测,具有良好的直观性,但对于局部点蚀、微裂纹等损伤,由于冲击时间较短,其在频率检测范围内的能量分量较小,采用常规的故障检测技术并不能达到理想的效果。针对该问题,文中提出基于小波预处理的神经网络技术的应用,通过对其数学模型的构建与参数调整,提升轴承故障信号的分析与处理能力,并采用数值模拟的方法验证其可行性。
1 滚动轴承故障诊断机理 1.1 故障特征频率滚动轴承产生早期缺陷或损伤的因素主要有材质缺陷、制造工艺不当、润滑不佳、氧化腐蚀等,经过一段时间的磨合,易出现疲劳剥落、磨损、裂纹等现象,影响机械设备的正常工作。不同的轴承故障会产生不同的周期性脉冲激励,根据谐振频率信号的采集和处理,并结合相应的数据分析技术,能够诊断出轴承的故障[4]。在工作中,轴承内圈故障频率为
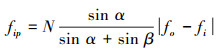 |
(1) |
轴承外圈故障频率为
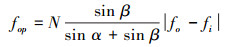 |
(2) |
滚动体的自转故障频率为
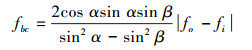 |
(3) |
式(1)~(3)中:α为滚珠与外滚道的接触角;β为滚珠与内滚道的接触角;N为轴承的滚珠数目;fi和fo分别为轴承内、外圈的转动频率。
1.2 诊断过程由于轴承的故障频率具有较宽的频域,在实际诊断过程中需要以某频段的高频固有振动为主要研究对象,通过信号采集和带通滤波得到分离后的故障频率。通过小波预处理,可高效地实现故障信号的信噪处理[5]。为了消除故障信号中的高频衰减成分,获取能够直接表现故障信息的低频包络信号,可运用Hilbert变换将分析对象进行包络解调[6]。同时,在神经网络技术的应用下,多分辨率的信号特征向量能够高效、精确地得出,其流程如图 1所示。
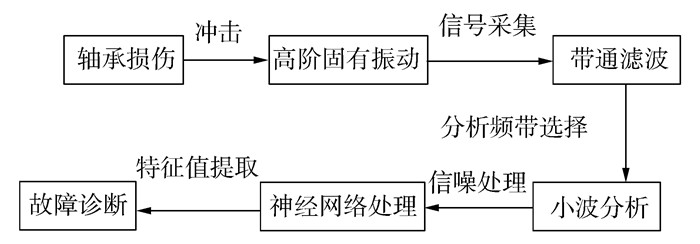
|
| 图 1 故障诊断过程 |
从信号滤波的角度来看,构建具有紧支性的正交小波有利于信号的隔点采样。高、低频信号分解后能够按照能量尺度大小分类,在神经网络算法下得到不同排列的特征向量。
1.3 紧支撑小波的构建小波分析是在传统的信号分析基础上发展而来的,具有紧支性特点,可将单一信号分解为不同频段的信号,广泛应用于信噪分离与弱信号提取,在轴承局部损伤的非平稳信号分析方面具有独特的优势。小波分析与处理方法主要有短时傅里叶变换、小波变换、Randon-Wigner变换、时频分析等。
对于模拟信号f(t)而言,其小波变换结果Wf(a, b)可表示为
式中:φab(t)为小波基函数φ(t)缩放与平移的结果。由于轴承的局部损伤信号属于典型的非平稳信号,在频检时具有较强的离散性,文中通过紧支撑小波的构建提升其信号处理的质量,此时,φ(x)为正交尺度函数。
支撑小波在构建时需要满足以下条件:
1) {φ(x-k)k∈z}具有标准正交性,且满足双尺度方程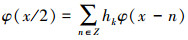
2) 满足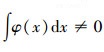
由支撑小波的构件条件可以推导出:
式中mφ(ξ)由两尺度方程的频域方程得出,其关系满足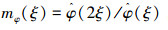
设(ξ)为三角多项式,N为自然数,此时紧支撑小波函数可通过以下方法得出:
2 小波神经网络的构建 2.1 小波神经网络结构基于小波预处理的神经网络技术在轴承局部损伤信号的处理中具有良好的应用效果[7]。通过小波变换能够对目标信号进行特定的多尺度缩放和平移,在具有自学习、自适应和容错性的神经网络算法下,通过网络参数的修正,能够使得模型结构更简单、计算的收敛速度更快[8]。
小波神经网络在结构上包括松散型和智能型两种,可通过伸缩和平移对信号进行多尺度调整,能够有效地提取故障信号的局部信息,其网络结构在网络权值和基函数之间保持线性关系,从而在局部优化计算时提升了收敛性。在小波基函数的作用下,依靠神经网络特定参数可解决常规神经网络算法的盲目性。
在基于小波预处理的神经网络根据维数可分为一维网络与多维网络。其中,一维神经网络只需进行一维小波变换,结构简单,是多维网络的基础;而多维神经网络则需要利用直积定义多维小波基,并运用张量积方法进行构造。在小波神经网络结构中,合理的初始参数选取对于整个网络模型的函数逼近与拟合性能有着重要的影响,当连续小波神经采用反向传播算法时,其收敛性并不理想,并且容易产生优化振荡以及局部极值等问题,因此,此种情况需要避免。文中对于小波神经网络的构建基于小波多分辨率分析以及多元时间序列分析。
2.2 小波基多分辨率分析小波基的多分辨率分析起源于S.Mallat的空间构造理论,即Mallat算法理论。在小波神经网络中,由于小波基函数之间并非完全独立并存在一定的线性相关,在框架内无法满足所有的正交性,导致信息存在冗余特征。文中通过基于多分辨率的分析方法,能够实现小波正交变换的快速构建,使得信号分解到指定的频带上,这对于信号的滤波有着重要的意义。
轴承故障信号的多分辨率分析实质为正交小波的滤波与分解[9]。通过高通与低通滤波器能够得到2组高低不同的信号,信号的每次分解均为原信号长度的一半,滤波与信号分解后隔点采样就能够避免冗余特征,并且保证信号质量。由于轴承的不同故障信号在各个频检范围内的能量不同,为了便于信号的处理,在进行特征向量求解的时候,可运用尺度排列方法。
2.3 多元时间序列分析在小波神经网络中,文中提出采用多元时间序列分析的方法确定神经网络的输入量,从而避免了人工输入带来的主观性,保证了网络的精度和效率。多元时间序列分析实质上为网络参数的估计计算,能够在修正模型下保持较低的误差,在信号的样本数据处理中具有良好的应用效果。对于小波神经网络模型的延迟阶数[10],可通过回归残差序列算法进行校验,结合多元时间序列的分析结果能够最终确定出合适的网络变量类型及数目。
3 小波神经网络的参数算法调整多维小波神经网络的输出结果可表示为
式中:m为输入层的节点数;k为隐含层的节点数;xj为网络的第j个输入节点;wij为输入节点j与隐节点i之间的权值;θ为输出阈值;ψi为作用函数;ai与bi分别为隐节点的缩放与平移参数。其中,作用函数ψi采用小波函数的形式可表示为
为了提升多维小波神经网络的自适应能力,文中通过对权值和阈值等参数进行修正的方法,提升样本运算效率,并降低小波输出的振荡性。小波神经网络的目标误差函数为
式中:dnp表示为隐含层第n个结点的期望输出;ynp表示神经网络实际输出;P(p=1, 2, …)为输出样本。为了使误差函数达到最小值,文中定义隐含层的输出Okp为
式中:xmp为输入层输入值;wkm为输入层的节点数m和隐含层的节点数k之间的权值;函数h表示Morlet小波函数。输入层与隐含层之间的权值经过调整后可表示为
式中:wnkold和wnknew分别表示修正前后的权值;Δwnkold为模型动量项;λ为动量因子;η为学习效率;模型输出层与输入层的权值修正方法一致。在小波神经网络的参数修正算法中,小波函数中的缩放参数经过调整后可表示为
式中:akold和aknew分别为修正前后的缩放参数,小波函数中的平移参数与缩放参数的修正方法一致。
4 数值模拟计算为了研究基于小波预处理的神经网络算法对轴承故障波形的处理能力及其参数调整后的收敛性,文中在样本数据下对滚动轴承内圈故障以及外圈故障的加速度振动幅值进行了基于MATLAB的数值模拟计算,通过迭代次数与误差的关系图,验证参数调整后的优化效果[11]。由于轴承局部损伤的故障频率较低,导致功率谱的分辨率不足,因此,在数值模拟计算时需要对小波系数进行重构。采用频谱细化理论提升小波神经网络的识别性,最终运用Hilbert包络解调法得到检波分析结果。
通过计算,得出轴承内圈与外圈的故障波形图分别如图 2、3所示,由图可以看出,波形图具有良好的分辨性,轴承内圈故障波的加速度振动频率更低,波峰分布相对稀疏,并且幅值明显大于外圈波形。由此可见,基于小波预处理的神经网络技术对于轴承的故障信号具有良好的处理效果。

|
| 图 2 轴承内圈故障波形 |
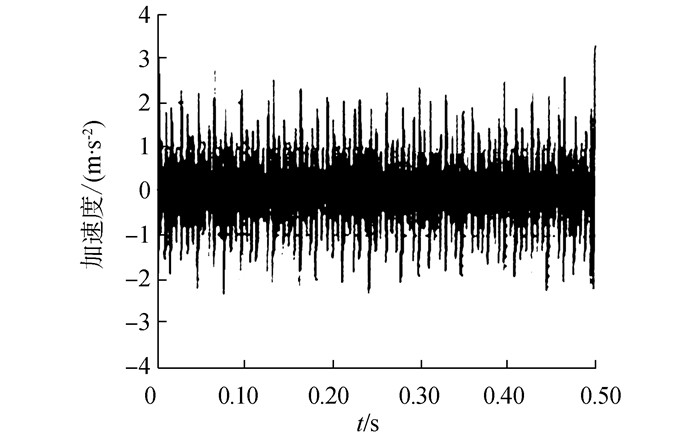
|
| 图 3 轴承外圈故障波形 |
在故障信号的处理过程中,随着模型维数增加,小波神经网络的结构将迅速增大,通过参数的修正能够降低目标误差并提升网络计算的收敛性,如图 4所示,在网络的信号压缩处理中,参数修正后的迭代误差在幅值和收敛效率上均优于修正前,由此可见,网络参数的修正对于故障诊断的准确度以及信号处理的能力均有重要的意义。
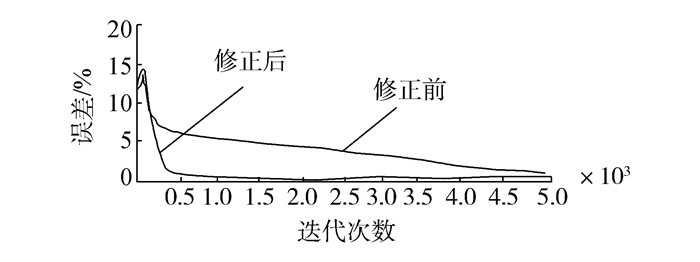
|
| 图 4 迭代误差曲线 |
基于小波预处理的神经网络技术在轴承的故障信号处理中具有良好的应用效果,经过参数修正后的网络结构在进行信号处理时具有更好地收敛性和更低的目标误差,在多元时间序列分析下,能够降低神经网络参数设计的盲目性。在小波预处理的神经网络中,虽然多维神经网络的理论尚不够成熟,但是在轴承等零件设备的故障诊断与信号处理中有着广阔的应用前景,这对于提升机械设备的可靠性,降低生产成本均有着重要的意义。
| [1] | 王斌.基于小波分析和BP神经网络的滚动轴承故障诊断方法研究[D].兰州:兰州交通大学, 2014:39-41. |
| [2] | 徐金梧, 徐科. 小波变换在滚动轴承故障诊断中的应用[J]. 机械工程学报 , 1997, 33 (4) : 50-55 |
| [3] | 万良虹.基于小波分析的滚动轴承故障诊断方法研究[D].北京:华北电力大学, 2004:2-4. |
| [4] | 张国远, 朱善安. 滚动轴承的自动监测及故障诊断系统[J]. 轴承 , 2005 (1) : 32-34 |
| [5] | 訾紫阳, 何正嘉, 张周锁. 小波分形技术及其在非平稳故障诊断中的应用[J]. 西安交通大学学报 , 2000, 34 (9) : 52-57 |
| [6] | 杨柳松.基于小波分析与神经网络滚动轴承故障诊断方法的研究[D].哈尔滨:东北林业大学, 2013:48-51. |
| [7] | 姜涛.基于改进小波神经网络的滚动轴承故障诊断[D].武汉:华中农业大学, 2013:29-38. |
| [8] | 岳红利.小波分形理论与神经网络结合的电机轴承故障诊断研究[D].太原:太原理工大学, 2011:32-38. |
| [9] | 李婧瑜, 李歧强, 侯海燕, 等. 基于遗传算法的小波神经网络交通流预测[J]. 山东大学学报:工学版 , 2007, 37 (2) : 109-112 |
| [10] | 单海欧, 李平. 小波神经网络的改进及应用[J]. 甘肃科学学报 , 2007, 19 (1) : 75-78 |