燃气轮机作为新型的动力设备,越来越受到人们的重视,其应用范围也越来越广,在航天航空领域燃气轮机是不可替代的动力设备,在航海和陆上交通领域的地位也越来越重要,其优点是结构紧凑、安全可靠、运行平稳、可以快速启动并带动负载,而且具有较高的热效率。由于其具有较高的热效率较小的排气污染特点,在电力和能源部门也逐渐成为原动机的主流产品。它们一旦发生事故就会给生产经营带来严重的影响和损失,因此及时诊断或避免处理燃气轮机运行故障和维护燃气轮机在正常状态下运行,就显得尤为重要[1]。近年来,故障诊断的方法有很多,主要包括:神经网络方法、支持向量机算法等。随着更广泛深入的研究和应用,人们发现SVM自身存在着许多不足之处,其主要表现在以下几个方面:1)为了限制其选择范围,选择核函数时必须满足Mercer条件;2)基本上基函数个数随训练样本集的规模呈线性增长状态,限制其规模的稀疏性;3)规则化系数和核函数的参数通常需要通过交叉验证等方法来获取,从而模型的计算量大大增加;4)预测的结果不具有统计上的意义,因此无法直接估计预测结果[2]。
2001年Micnacl E.Tipping在贝叶斯学习理论的基础上提出了一种新的机器学习方法——相关向量机算法(RVM) 。该算法是一种与支持向量机类似的稀疏性概率模型,它既保持了支持向量机在小样本训练中泛化性能好、分类能力强、适合处理高维非线性问题的特点,而且很大地提升了解的稀疏性、算法的鲁棒性及分类的准确。文中提出基于遗传相关向量机的分类方法,用遗传算法对相关向量机中的核函数的核参数进行了优化。
1 遗传相关向量机理论 1.1 相关向量机回归算法如果输入-输出数据集{xn,tn}n=1N,假设目标是一个有附加噪声的模型样本[3]:



Φ=[φ(x1),φ(x2),…,φ(xN)]T
其中:φ(xn)=[1,K(xn,x1),K(xn,x2),…,K(xn,xN)]T
在贝叶斯的框架下,权值w可以通过极大似然法求得,RVM为每一个权值定义了高斯先验概率分布来约束参数,这样可以避免过学习现象: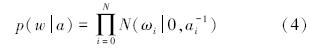
通过计算,在已经定义了先验概率的前提下,根据贝叶斯准则,得到如下后验概率:
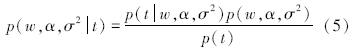
给出了一个新的测试样本xΦ,预测相应的目标tΦ,按照预测分布:
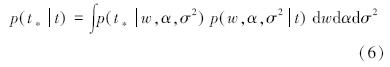
必须寻找一个相对有效的方式来应对这些这样的连续分布的计算,因此我们找到一个相对有效的近似[4]。
无法直接计算(5)式中的后验概率p(w,a,σ2t),因为无法计算积分p(t)。然而可以将后验概率分解成为



现在,对于相关向量“学习”已成为寻找超参数的后验形式。例如关于α和σ的p(a,σ2|t)∞p(t|a,σ2)p(a)p(σ2)的最大化。仅需要使p(t|a,σ2)最大[5, 6]。
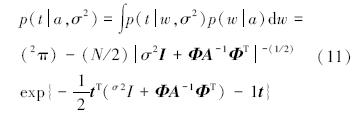
因为不能在封闭的形式中得到使式(11)最大的α和σ2的值,因此需总结迭代估计规则。按照Mackay的方法,得到α值,令式(11)的值为零,整理后给出:

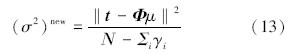
从式(8)可知,p(wi|t,a,σ2)在零值处是趋于无穷的。消减相应的基函数,实现稀疏特性[7, 8]。
1.2 相关向量机分类器由于相关向量机的分类模型和回归模型都是基于同一个框架,所以下面篇幅只针对二分类问题来说明,设训练样本集合为
(xn,tn)(n=1,2,…,N,x∈Rd,t∈{0,1}类别标号),RVM的分类函数定义为
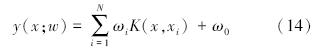
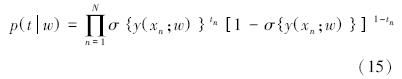
在贝叶斯框架下,获得权值w可以采用极大似然法,但为了防止“过学习”现象出现,定义权值的先验概率分布如下:

对于分类问题,与回归模型的情况不同,由于不能计算出其后验概率,因此需要用狄拉克函数进行近似:
a) 对当前固定的α值,求最大可能的权值wMP。因为p(w|t,α)∝p(t|w)p(w|α),这相当于求使式(16)最大的wMP值。对于式(17)采用二阶牛顿法wMP。

b) 采取拉普拉斯算子方法二次逼近对数后验概率。然后对(17)式两次求导得出:

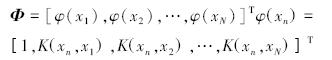
c) 利用Σ和wMP,不断对α进行训练更新,直到达到适当的收敛尺度:

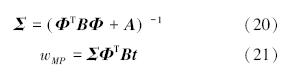
通过以上介绍,相关向量机步骤如下:
1)从选择合适的核函数开始,将低维向量向高维空间映射。
2)初始化α和σ2。在对α和σ2进行迭代前,需要对这两者进行初始化,虽然初始化的值对结果影响不大。
3)计算μ和Σ。RVM回归问题中μ=wMP=ΣΦTΒt,Σ=(σ-2ΦTΦ+A)-1;RVM分类问题中μ=wMP=ΣΦTΒt,Σ=(ΦTΒΦ)-1。
4)然后根据式(12)、(13)对α和σ2进行重新估计。
5)重复步骤3),直到得到合适的结果为止。
6)利用得到的结果继续对新数据进行预测。
1.3 基于遗传算法的RVM参数选取文中利用遗传算法(GA)对RVM算法的参数进行优化设置。由于在RVM算法分类的准确度上参数的选取起着决定性的作用,与之前的人为列举寻优、交叉验证等方式寻找参数相比,遗传算法没有局部最优缺陷,而且用时最短。
遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法,该算法的优点在于不依赖传统的梯度信息,所以不存在求导和函数连续性的限定问题,其全局搜索方式是利用选择、交叉和变异等遗传操作来进行的,适用于全局性并行处理并具有算法简单、通用性强和鲁棒性强的特点,在优化组合问题的求解、机器学习、软件学习、软件技术、图像处理、模式识别、神经网络、工业优化控制、故障诊断、人工生命、社会科学等方面得到了广泛的应用,并且GA在实际应用中也取得了巨大成功。这个过程就像自然界中的改造一样,导致种群中个体的进化,得到的新个体比原个体更能适应环境[9, 10]。
 |
| 图 1 GA算法流程 |
文中主要利用遗传相关向量机对涡轮叶片的温度信号进行分析并对故障的分类,实验中提取了正常状态、整体温度过高、局部温度过高3种状态下的数据各20组,如图 2所示。
 |
| 图 2 叶片在3种工况下的温度数据 |
对数据进行预处理、信号分割、EMD分解3个步骤来提取特征向量,最后利用遗传相关向量机进行故障的分类,简述3个步骤如下:
1)数据预处理。由于设备之间互相干扰,在温度信号采集的过程中,会在测量信号中参杂一些不必要的多余信号,对论文所需要提取的信号造成一定的影响,进而影响了信号特征的提取,因此在进行叶片的温度数据分割之前需要对采集到的数据进行预处理。已经知道温度信号是一组缓慢变化的波形,而干扰信号的变化比较剧烈,因此论文采用利用 离散傅里叶变换和低通滤波的方法进行滤波。
2)特征向量提取。采用最大值分割法对经过滤波后的信号进行分割,经过反复计算实验得到86个叶片为一个周期的信号波形。然后要在不同的工况下分离出单个叶片的温度信号因为不同工况下有着不同的叶片间隔。通过引入EMD方法对单个叶片故障信号进行分离,得到IMF分量,不同的温度信号IMF分量的个数不同,选择前n个具有故障信息的分量作为研究对象。再计算前n个IMF分量的能量:
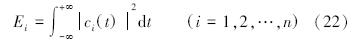
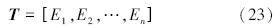

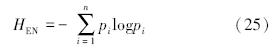
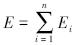 中的比重,通过式(25)计算3种状态下涡轮叶片的EMD能量熵值如表 1所示。
中的比重,通过式(25)计算3种状态下涡轮叶片的EMD能量熵值如表 1所示。
表 1表明正常状态下涡轮叶片的能量熵应该是最大的,因为正常情况下涡轮叶片温度分布相对平均。当发生断裂或者局部规格不同时,造成局部温度过高,温度分布不均匀。同样的整体温度过高时也会造成温度分布不均匀,使得能量熵值减小。为了便于处理对T进行归一化处理:

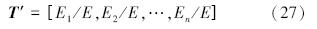
3)将提取的60组特征向量随机分成两组,训练样本组包括48个样本,测试样本组包括12个样本,通过遗传相关向量机得到最后的结果 3 实验仿真与分析
文中采用MATLAB进行仿真。遗传相关向量机的故障诊断模型如图 3所示。
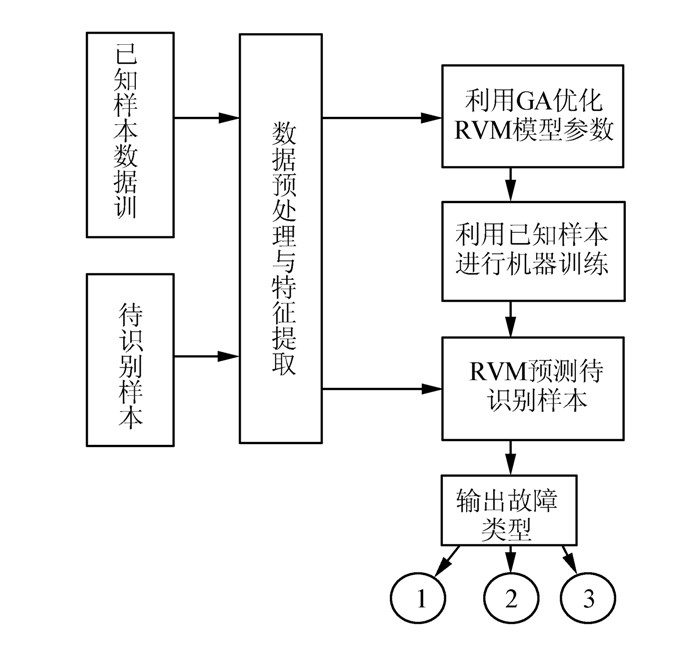 |
| 图 3 涡轮叶片故障诊断模型 |
模拟故障数据各6组,对模拟的涡轮叶片故障信号进行EMD分解,然后求其IMF的能量,由于故障信息主要集中在前几个分量中,因此文中选用前8个分量,残余项的能力几乎为零。然后求得特征向量T′=[E1/E,E2/E,…,En/E],整理得表 2。
| 叶片 状态 | 信号 状态 | 前4个特征向量 | |||
| E1/E | E2/E | E3/E | E4/E | ||
| 1 | 0.763 5 | 0.637 1 | 0.098 6 | 0.034 7 | |
| 2 | 0.740 3 | 0.664 8 | 0.096 0 | 0.021 7 | |
| 正常 | 3 | 0.764 4 | 0.630 6 | 0.128 0 | 0.037 4 |
| 4 | 0.738 8 | 0.667 3 | 0.090 5 | 0.020 6 | |
| 5 | 0.778 2 | 0.613 5 | 0.124 7 | 0.047 2 | |
| 1 | 0.921 8 | 0.355 1 | 0.149 3 | 0.040 8 | |
| 局部 | 2 | 0.933 9 | 0.332 0 | 0.126 5 | 0.033 8 |
| 温度 | 3 | 0.925 6 | 0.362 0 | 0.103 3 | 0.035 2 |
| 过高 | 4 | 0.927 3 | 0.341 1 | 0.149 5 | 0.034 1 |
| 5 | 0.931 8 | 0.338 5 | 0.122 7 | 0.042 1 | |
| 1 | 0.901 8 | 0.424 7 | 0.073 0 | 0.027 4 | |
| 整体 | 2 | 0.901 6 | 0.420 2 | 0.098 0 | 0.027 4 |
| 温度 | 3 | 0.910 1 | 0.403 6 | 0.090 5 | 0.021 6 |
| 过高 | 4 | 0.873 8 | 0.466 4 | 0.130 2 | 0.037 3 |
| 5 | 0.892 3 | 0.440 9 | 0.091 0 | 0.028 2 | |
通过模拟故障数据,利用故障信息根据式(27)的特征向量如表 2所示,遗传算法中随机产生初始代群体,群体规模为50,迭代次数设为30,交叉概率设为0.4,变异概率设GA算法得到相关向量机核函数的核参数为2.95。
通过与普通相关向量机、普通支持向量机以及BP神经网络方法做对比来突出文中的遗传相关向量机方法的优越性和有效性。
实验中以分类正确率来衡量分类的优越性。实验结果如表 3所示。
GA-RVM算法的分类正确率为98%,RVM算法的分类正确率为92%,SVM算法的地分类正确率为83.5%,BP神经网络的分类正确率为74%,且分类结果不稳定。可见,遗传相关向量机的故障分类方法比相关向量机、支持向量机、BP神经网络的分类准确率都要高。
在故障诊断过程中,相关向量数的多少直接影响了故障诊断的快慢,表 4是SVM,RVM以及GA-RVM算法在故障诊断过程中所用的相关向量数。
通过表 4可知,SVM所需相关向量数最多,故障诊断最慢,其余两种诊断速度相当。
4 结束语文中研究了基于遗传算法优化的相关向量机的燃机涡轮叶片故障诊断方法,仿真结果表明,文中研究的GA-RVM方法的故障分类正确性要优于RVM算法、SVM算法和BP神经网络方法,实验验证了GA-RVM在燃机涡轮叶片故障诊断中的有效性和优越性。
| [1] | 李旭, 徐心和. 遗传算法在故障诊断专家系统中的应用[J]. 控制与决策, 1998, 13(4):377-380. |
| [2] | 史东锋, 屈梁生. 遗传算法在故障特征选择中的应用研究[J]. 振动、测试与诊断, 2000, 20(3):171-176. |
| [3] | 梁化楼, 戴贵亮. 人工神经网络与遗传算法的结合:进展及展望[J]. 电子学报, 1995, 23(10):194-200. |
| [4] | 熊凌, 赵明旺. 基于遗传算法的BP网络全局收敛的混合智能学习算法[J]. 武汉科技大学学报:自然科学版, 2000, 23(2):183-186. |
| [5] | 唐昌盛, 曲建岭, 于建立. 基于支持向量机的航空发动机故障诊断研究[J]. 测控技术, 2008, 27(4):13-14. |
| [6] | 王雪飘, 李学仁, 吴志强. 粗SVM方法及其在发动机故障诊断中的应用[J]. 微计算机信息杂志, 2008, 24(31):189-191. |
| [7] | 杨树仁, 沈洪远. 基于相关向量机的机器学习算法研究与应用[J]. 计算技术与自动化, 2010, 29(1):43-47. |
| [8] | 李敏强, 寇纪凇, 林丹, 等. 遗传算法的基本理论与应用[M]. 北京:科学出版社, 2002. |
| [9] | HOLLAND J H. Adaptation in natural and artificial systems[M]. Ann Arbor:University of Michigan Press, 1975. |
| [10] | CHANG E J, LIPPMANN R P. Using genetic algorithms to improve pattern classification performance[R]. San Mateo:Advance in Neural Information Processing, 1991, 797-803. |



