2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
国内外的专家学者在缆绳的仿真建模以及动力学特性方面已经做了大量的研究: Sun[1]、Milinazzo[2]对动态海缆受力模型进行了研究;吴常林[3]基于集中质量方法,利用经典的弹簧质点模型对撇缆绳进行了数学建模,在弹簧质点模型的基础上,将质点近似为集中质量的球单元,弹簧近似为具有一定质量的杆单元,引入了Kawabata拉伸张力模型,考虑了空气动力的影响,建立了撇缆绳运动的数学模型;靳明君[4]等人根据悬索微元力学平衡关系,对悬索微元进行积分,最终推导出了计算悬链线长度的显式表达式,该方法对于缆绳的绘制提供了一种新的思路;王飞[5]基于集中质量法建立了三维非均匀拖缆在规则波作用下的数学模型,利用四阶龙格库塔方法进行了数值求解,讨论了拖缆在不同波浪作用下的稳态响应特性;赵国伟[6]等基于离散质点系统假设,将柔性绳索体的结点近似为集中质量球单元,结点间近似为杆单元,引入Kawabata拉伸张力应变模型,考虑空气动力影响,建立柔性绳索体的动力学方程,运用四阶Runge-Kutta法进行数值计算,根据能量损耗量对速度修正,基于OpenGL后处理显示,实现了对绳索体运动过程的仿真;秦道武[7]等提出了一种基于凝集质量法的海洋缆索动态响应研究的模型,该模型采用Kane方法以广义主动力与广义惯性力相平衡的方式得到缆索运动的控制方程;胡晓楠[8]等人基于有限元法,考虑空气阻力、重力的影响,研究了绳索单元的力学模型,在ANSYS/LSDYNA软件中采用Link167单元建立柔性绳索的动力学分析模型,提出了空气阻力计算、运动状态参数提取和通过载荷曲线迭代的方式模拟空气阻力的方法,完成了柔性绳索在空气阻力作用下的运动仿真,仿真结果与实验结果有较高的一致性,证明了该仿真方法是切实可行的;刘鑫[9]在大连海事大学V.Dragon3000系列模拟器的基础上分析了缆绳在靠离泊作业时的张力模型并计算了缆绳在满足和不满足胡克定律两种情况下的张力大小,利用弹簧-质点模型的方法建立了缆绳的受力模型并实现了对缆绳绞缆、出缆过程的仿真。缆索的动力学建模可以划分为两大类:一类是偏微分方程形式的连续模型,另一类是常微分方程形式的离散化模型[10],文中提出一种离散化的缆索动力学建模方法,用于海上吊放系统的动力学分析。 1 理论计算
缆绳具有“可拉不可压”的特殊性质,其动力学特性和刚体有较大的区别[11]。为分析缆绳受力及变形,文中将整根缆绳用许多集结质量mi(i=1~n+1)取代,并将相邻的两个集结质量以一根无质量,长度为λi的均匀段绳连接。将各个集结质量所占据的位置称为“点”,根据平衡方程和几何方程,拖缆上受重力、水动力和惯性力作用。拖缆上任一点的力的平衡方程如式(1):
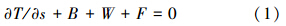
B→=-[{m1r→-ρA[J→+(U→·t→)t→]}/S′]
T表示缆绳的张力YiL;ψiL表示重力浮力之差;F表示为在水中的流体阻力MiL。定义初始条件和边界条件,分析缆绳在吊放过程中各个点的速度变化,进而将在运动坐标系下所得到的速度转换到固定坐标系下,积分求得点位移的变化,并且类似解得第i个点缆绳在吊放过程中所受到的张力、剪力等参数变化,得到第i点左右两边关系式,利用矩阵变换求出i点左右的转移矩阵;将承担整根连续缆绳弯曲劲度的各无质量均匀段绳称为“场”,根据平衡方程和几何方程,得到第i场前后的关系式,利用矩阵表示,求出第i场前后的转移矩阵;将一个“点”及一个相邻的“场”合并为一个“段”,通过第i节点处的点转移矩阵和场转移矩阵得到第i段的转移矩阵,通过迭代最终得到缆绳左右两边界处的总转移矩阵。最后通过缆绳总转移矩阵和左端的边界条件,由各个区段转移矩阵的连乘运算求得缆绳各段受力及变形。实际计算时,我们可以采用试根的方法,先假设缆绳的一个自然频率值,代入总转移矩阵,看能否满足子矩阵行列式为零。当然大多数情况下是不为零的,则再重新假设另一个值。重复上述的所有步骤,一直到两次行列式的(正、负)符号相反,此时二者的均值即可近似为缆绳的一个自然频率。 2 点转移矩阵将各个集结质量所占据的位置称为“点” ,如图 1,根据平衡方程和几何方程,得到第i点左右两边关系式(2),利用矩阵变换求出i点左右的转移矩阵。
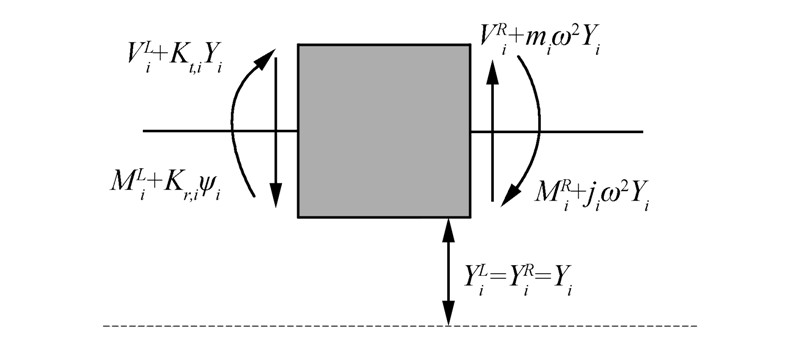 |
| 图 1 第i个点的平衡方程 |
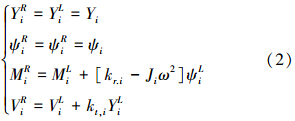
令{δ}iR={YiR ψiR MiR ViR}、{δ}iL={YiL ψiL MiL ViL},将式(1)表示成{δ}iR=[TS]{δ}iL,则求出i点的转移矩阵:
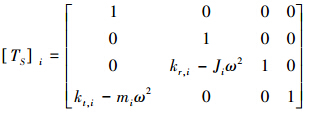
将承担整根连续缆绳弯曲劲度的各无质量均匀段绳为“场”,如图 2,根据平衡方程和几何方程,得到第i场前后的关系式(3),利用矩阵变换求出i场前后的转移矩阵。
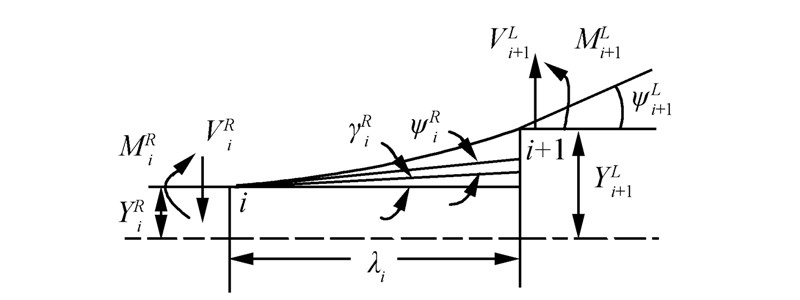 |
| 图 2 第i个场的平衡方程 |
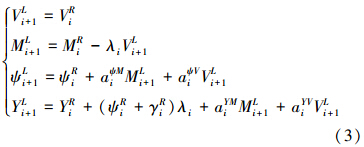
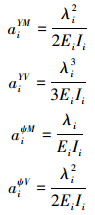
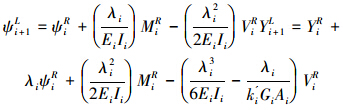
{δ}i+1L={Yi+1L ψi+1L Mi+1L Vi+1L}
{δ}iR={YiR ψiR MiR ViR}
将式(3)表示成{δ}i+1L=[TF]i{δ}iR,则第i个场的转移矩阵: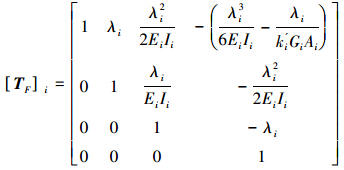
区段是由点与场所构成,故其转移矩阵可以由点的转移矩阵与场的转移矩阵求得,从式(2)及式(3)可得{δ}i+1L=[TF]i[TS]i{δ}iL=[T]i{δ}li,则第i段的转移矩阵为
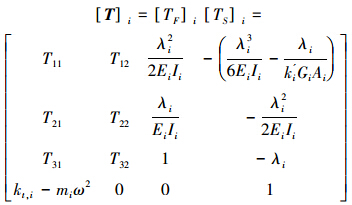
式中:
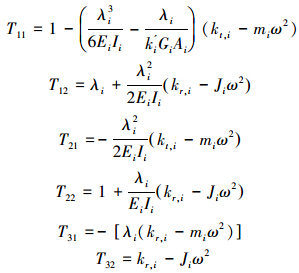
{δ}i+1L={Yi+1L ψi+1L Mi+1L Vi+1L}
依次迭代可以求出:
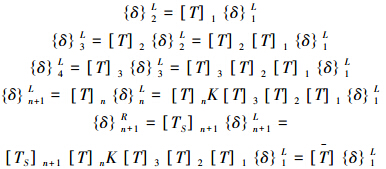
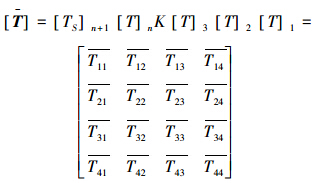
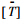 为整跟缆绳的总体转移矩阵。其阶数是4阶。它可以求得缆绳左端的状态{δ}1L={Y1L ψ1L M1L V1L}与其右端状态{δ}n+1R={Yn+1R ψn+1R Mn+1R Vn+1R}的关系为
为整跟缆绳的总体转移矩阵。其阶数是4阶。它可以求得缆绳左端的状态{δ}1L={Y1L ψ1L M1L V1L}与其右端状态{δ}n+1R={Yn+1R ψn+1R Mn+1R Vn+1R}的关系为
缆绳在起吊过程中,由于部分缆绳暴露在空气中,缆绳受到的外界条件不同,根据连续性方程,自由液面处缆绳所受到的张力与位移相同。通过Matlab编程,定义边界条件,自由液面上方受到的是空气流场作用,而自由液面下方则是水的流场作用。最后通过缆绳总转移矩阵和左端的边界条件,求得缆绳各段受力及变形。 5 仿真实验
基于上述缆绳模型进行吊装实验仿真,实验模型为钢架结构,长度l随下潜时间变化而变化,最终下潜60 m(水上10 m,水下50 m,程序中并无上限要求,下潜深度可增大),设计半径为50 mm,材料系数采用Q235钢,模型初始状态为铅锤,底部作用集中载荷发生变化,重量从1.5吨增至2.5吨,每隔0.2吨增长计算一次。水上部分不受侧向力,水下部分侧向有水流压力,压力值与铅垂重量相关,变化范围为0.05 N/mm(50 N/m)变化至0.1 N/mm(100 N/m),每组数据增长步长为0.01 N/mm。钢架横截面积同样也随铅垂重量变化而变化,其横截面半径由0.01 m增长至0.06 m,增长步长为0.01 m。分6组进行仿真实验,如表 1所示。
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 铅垂重量/t | 1.50 | 1.70 | 1.90 | 2.10 | 2.30 | 2.50 |
| 横截面半径/m | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 |
| 水流速度/(N·mm-1) | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | 0.10 |
得到了6组实验结果。
第1组:绳索下放的姿态示意图,如图 3,从左到右依次为下放10、20、30、40、50、60 m的姿态。
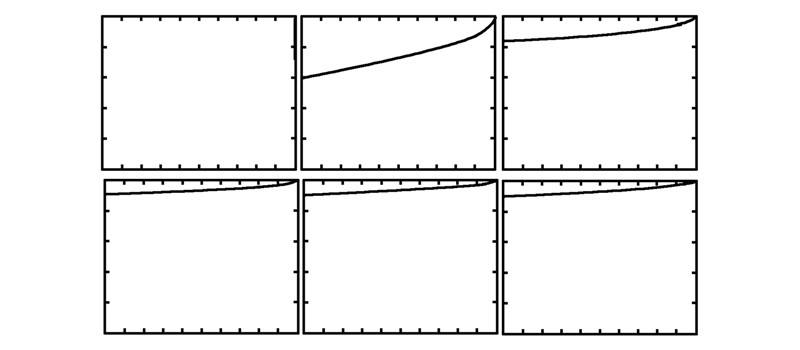 |
| 图 3 第1组实验结果 |
第2组:绳索下放的姿态示意图,如图 4,从左到右依次为下放10、20、30、40、50、60 m的姿态。
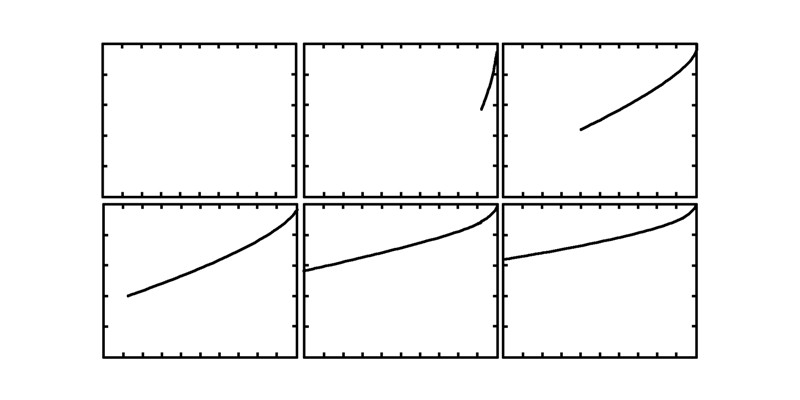 |
| 图 4 第2组实验结果 |
第3组:绳索下放的姿态示意图,如图 5,从左到右依次为下放10、20、30、40、50、60 m的姿态。
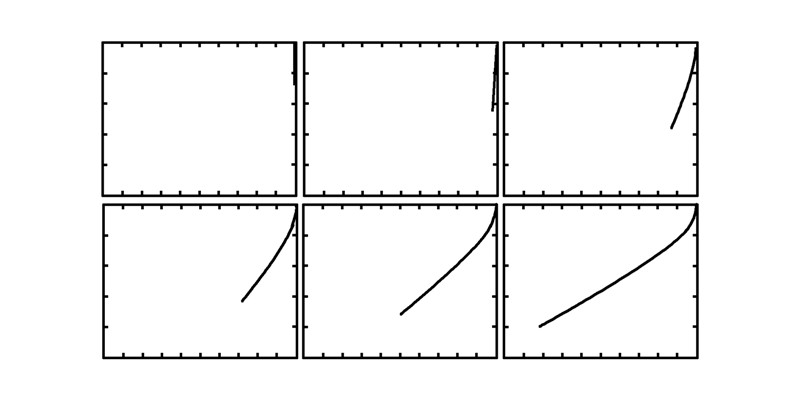 |
| 图 5 第3组实验结果 |
第4组:绳索下放的姿态示意图,如图 6,从左到右依次为下放10、20、30、40、50、60 m的姿态。
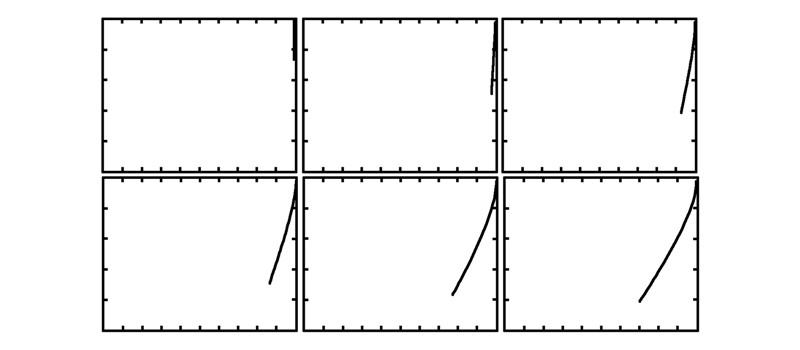 |
| 图 6 第4组实验结果 |
第5组:绳索下放的姿态示意图,如图 7,从左到右依次为下放1、20、30、40、50、60 m的姿态。
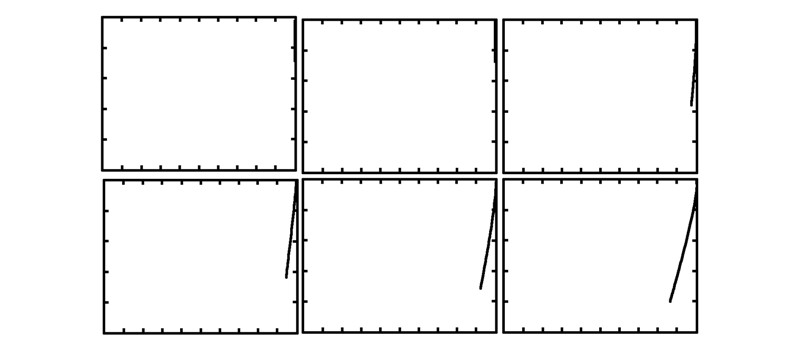 |
| 图 7 第5组实验结果 |
第6组:绳索下放的姿态示意图,如图 8,从左到右依次为下放10、20、30、40、50、60 m的姿态。
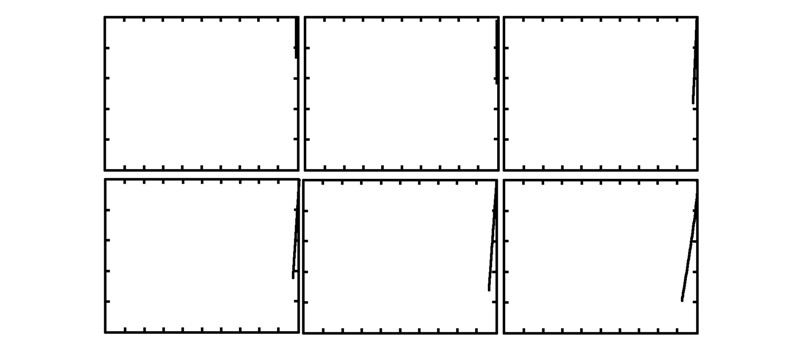 |
| 图 8 第6组实验结果 |
通过对各工况下的实验结果的分析,铅垂重量在2.3~2.5 t和绳子半径在0.05~0.06 m时,重锤着地点偏差不会很大,能够满足焊接要求。 6 结束语
文中基于有限元法,研究了绳索单元的力学模型,广义主动力与广义惯性力相平衡的方式得到缆索运动的控制方程,建立了柔性绳索体的动力学方程,并考虑实际海上做业因素的影响,仿真实验中加入空气阻力、重力、海流作用力,实现了从水上到水下吊装过程的数学建模,并基于该缆索数学模型进行了海上吊装的仿真实验,从实验结果可以清晰的看出每种工况下的缆索姿态,以及吊重到达预定深度的的下放位置,能够为海上吊装提供可靠保证。
| [1] | SUN Yang, LEONARD J W. Dynamics of ocean cables with local low-tension regions[J]. Ocean engineering, 1998, 25(6):443-463. |
| [2] | MILINAZZO F, WILKIE M, LATCHMAN S A. An efficient algorithm for simulating the dynamics of towed cable systems[J]. Ocean engineering, 1987, 14(6):513-526. |
| [3] | 吴长林. 航海模拟器中缆绳作业的仿真研究[D]. 大连:大连海事大学, 2012:1-70. |
| [4] | 靳明君, 张志国. 悬链线柔索索长的计算[J]. 铁道标准设计, 2004(5):9-10. |
| [5] | 王飞, 黄国樑, 刘天威. 规则波作用水下拖缆数值分析研究[J]. 海洋工程, 2006, 24(1):92-97. |
| [6] | 赵国伟, 熊会宾, 黄海, 等. 柔性绳索体展开过程数值模拟及实验[J]. 航空学报, 2009, 30(8):1429-1434. |
| [7] | 秦道武, 朱克强, 朱艳杰. 基于凝集质量法的海洋缆索动态响应建模与仿真[J]. 港工技术, 2014, 51(3):7-10. |
| [8] | 胡晓楠, 张建斌, 赵国伟. 柔性绳索在空气阻力作用下的动力学仿真研究[J]. 机械科学与技术, 2010, 29(10):1334-1337. |
| [9] | 刘鑫. 航海模拟器视景中缆绳的绘制[D]. 大连:大连海事大学, 2011:1-35. |
| [10] | 王鹏. 拖曳式诱饵弹释放过程绳索动力学仿真研究[D]. 长沙:国防科学技术大学, 2011:8-20. |
| [11] | 丁娣. 载人飞船大型降落伞回收系统中几个动力学问题研究[D]. 长沙:国防科学技术大学, 2011:14-27. |



