随着网络化、信息化的不断发展以及防御系统的不断增强,单枚导弹的突防和攻击能力变弱,研究多枚导弹的协同作战尤为重要[1]。多枚导弹协同作战需要动态信息交互,要打破传统作战中导弹之间没有联系的思想[2]。如果多导弹同时击中目标,会对对方的导弹防御系统造成极大的压力,因为它不能对所有的导弹进行反应,从而提高导弹打击能力。因此研究信息交互条件下具有时间约束的导弹协同有非常重要的意义。
关于制导律中时间约束的问题是近几年才开始研究的,文献[3]首先提出了时间约束的问题,给出了具有导引时间约束的制导律(impact-time-control guidance,ITCG)并应用在了反舰导弹齐射攻击中。该制导律在比例导引的基础上增加附加项进行修正,进而推导出了线性形式的解决方案。文献[4]提出了另外一种具有导引时间限制的制导律,它使用了一个随时间变化的导航系数作为控制参数,从而达到了具有时间约束的目的。但是这两种制导律都没有考虑导弹的通信问题,即假设导弹间没有动态的信息交互,因此并没有实现真正意义上的协同。
目前协同控制已经应用到了多个领域,如无人机[5],机器人[6]和导弹[7]等。文献[8]提出了一种通用的解决协同控制的方法,即基于协调变量的方法。文献[9]利用协调变量的方法实现了无人机的协同控制。但是协同控制应用在导弹上的研究还比较有限,导弹速度比无人机速度快,要求实时性更高,相对更难控制。
为了解决多导弹相互通信情况下的协同问题,本文提出了时间约束制导律和一致性算法相结合的制导方法,能够实现有一定拓扑结构的多导弹在指定时刻击中目标的任务。这种制导方法协同速度快且有较好的性能。
1 有指定导引时间约束的CPN制导律
In-Soo Jeon提出了一种有指定导引时间约束的多导弹协同攻击制导律CPN[4](cooperative proportional navigation),该制导律是基于寻的制导律提出来的,这里的协同攻击指的是多枚导弹同时攻击同一目标或者多个目标。在CPN制导律作用下,多枚导弹可在预先指定的导引时间下击中目标。假设有m枚导弹参与到协同攻击,二维平面内的弹目运动关系如图 1所示。
 |
| 图 1 弹目运动关系 |
θ、η、λ分别表示导弹的速度方向角、前置角和视线角;M、O表示导弹和目标,其中Mi表示的是第i枚导弹;Vi、Vo表示第i枚导弹的速度和目标的速度;第i枚导弹的法向加速度为ai。假设导弹的速度是常值,各导弹的初始速度大小可以不一样,但它们都有相同的任务,即在同一指定时刻击中目标。下面是导弹i与目标O的相对运动方程:

假设目标位于原点静止不动,则ao、Vo都为零,式(1)可表示为
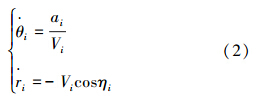
在传统的PN(proportional navigation) 导引律作用下,导弹的法向加速度如下[10]:

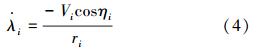
为了解决有指定导引时间约束的导弹协同问题,要选择一个时变的导航系数Ni来控制导引时间,则导弹法向加速度如下:
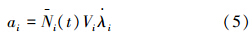
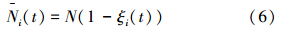
定义剩余飞行时间误差ΔTi:
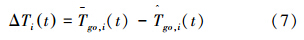
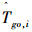 (t)为导弹的剩余时间;假设前置角ηi很小,
(t)为导弹的剩余时间;假设前置角ηi很小,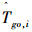 (t)可以表达为
(t)可以表达为
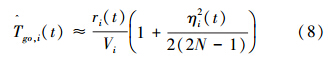
增益因子ξi(t)的表达式为
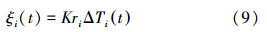

即在CPN制导律下,由式(5)、(6)和式(10)可得到导弹的法向加速度的表示形式如下:
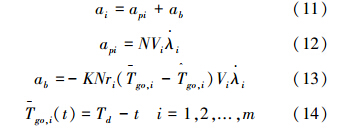
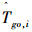 作用到导弹上,改变导弹轨迹,使导弹剩余时间趋于指定时间,从而实现在同一时刻击中目标,达到协同。因此ΔT收敛到0的速度代表实现协同的速度。
作用到导弹上,改变导弹轨迹,使导弹剩余时间趋于指定时间,从而实现在同一时刻击中目标,达到协同。因此ΔT收敛到0的速度代表实现协同的速度。对于一个合适的非负的增益K[4],CPN制导律能够使多导弹在相同时刻击中目标。
在具体实现时,事先选择一个合适的指定导引时间Td,Td通过式(13)、(14)作用到导弹上,导弹通过改变飞行路径实现时间上的协同。
文献[3]指出若CPN制导律能正常作用,则Td须满足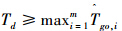 ,即外部指定导引时间不小于任何一枚导弹的飞行时间。
,即外部指定导引时间不小于任何一枚导弹的飞行时间。
这种制导律虽然能够实现多导弹在时间上的协同,但是这个时间是人为事先指定的,动态性差,且没有考虑到导弹间的通信问题,因此要实现真正的导弹协同需要考虑导弹间相互通信的问题。
本文主要研究基于相互通信的多导弹协同,要通过设计通信拓扑结构和借助基于协调变一致性算法来实现。
2 图中的一致性问题 2.1 图的基本知识
图论所研究的图是客观世界中某些具体事物间联系的一个数学抽象。在研究多导弹,多无人机时可以把它们抽象成一个图[11],用图论去分析。用点表示系统中的个体,用边表示个体间的联系[12]。
一个有向图G由非空有限集V,E,A构成,称G=V,E,A为一个图。V和E表示有向图G的顶点集合和边的集合,A为图的邻接矩阵。
其中索引集合为I=1,2,...,n,且i,j∈I; V=v1,v2,…,vn表示G有n个顶点;E=eijV×V表示两点之间的边,eij=(vi,vj)或eij=(i,j)表示从顶点vj到顶点vi的边,边eij的权值对应邻接矩阵A中的邻接元素aij。(i,j)∈E表示图G中从vj到vi的边存在,即节点vi能够接收到节点vj发出的信息。
A=[aij]∈Rn×n(i,j=1,2,...,n),若(i,j)∈E,则相应的aij=1,否则aij=0。Ni={vj|(vi,vj)∈E}表示顶点vi的邻居,顶点vi能够接收到其邻居点的信息。
2.2 协调一致性
在一个多主体系统中,通过与周围节点的相互通信从而在某个意见上达到一致,就称为协调一致性。 对于时间连续系统,协调一致性的算法可以表示为[13, 14]
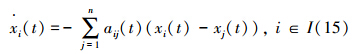
式(15)又可写成如下矩阵形式:

式中:x(t)=[x1(t),x2(t),…,xn(t)]TLt=[lij]∈Rn×n是图G的拉普拉斯矩阵,其定义如下:
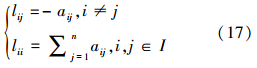
定义1 对于、∀xi0i,j=1,2,...,n,当t→∞时有xi(t)-xj(t)→0,此时称系统实现了协调一致。
对式(16)求解,可得到:
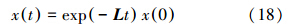
对exp-Lt精确求解,就可以得到群体的决策值xt。
定理1 如果G是一个强连通的图,并且该图的拉普拉斯矩阵满足Lωr=0,ωTlL=0并且ωTlωr=1,那么下式成立:

3 协调一致算法
协调算法采用一种双层制导结构[15],它由协调层和控制层组成,如图 2所示。连接这两层的变量称作协调变量。CPN制导律具有一个“可控量”即指定导引时间Tgo,i(t),所以把它取为协调变量。
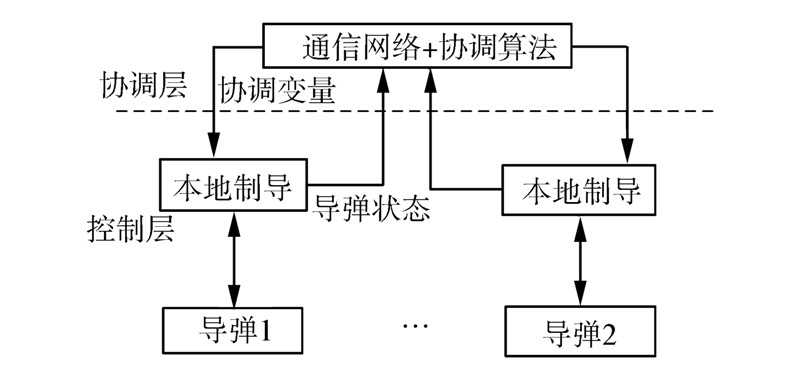 |
| 图 2 协调策略示意 |
协调层利用相邻运动体之间的相互通信实现信息交流,并利用上文提到的协调一致性算法计算协调变量,在这里协调变量是协同时间。控制层采用以上所述的有时间约束的制导律对运动体进行控制。在具体实现过程中控制层首先把各导弹的状态(如位置,速度,剩余导引时间估计值等)发送到协调层,经过式(15)的协调一致算法使协调变量Tgo,i趋于一致,然后下发到各导弹,经过导引律的作用,是导弹实现协同。
协调一致的过程也就是各个导弹根据相邻导弹修正自己的协调变量值Tgo,i的过程,即Tgo,i是由各个运动体的协调变量逐渐收敛趋于一致而得到的。
假设有3枚导弹参与齐射攻击,其拓扑结构如图 3所示。xi代表第i枚导弹对集结时间的理解,也就是xi=Tgo,i,这样得到一致性协调算法:

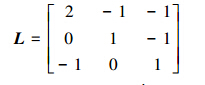
根据Tgo,i0≥maxmi=1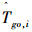 ,选取合适的Tgo,i0,根据定理1,对于i=1,2,3满足T*go,i=
,选取合适的Tgo,i0,根据定理1,对于i=1,2,3满足T*go,i=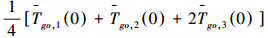 ,t→∞ ,也就是最后3枚导弹的导引时间是一样的,达到了时间协同的目的。
但在实际应用中,不可能用无穷长的时间来使它收敛到最后的值,一般会给一致性算法指定一个周期ΔT,在t=ΔT时就把Tgo,iΔT作为指定导引时间,尽管还没有完全收敛到T*go,i。
,t→∞ ,也就是最后3枚导弹的导引时间是一样的,达到了时间协同的目的。
但在实际应用中,不可能用无穷长的时间来使它收敛到最后的值,一般会给一致性算法指定一个周期ΔT,在t=ΔT时就把Tgo,iΔT作为指定导引时间,尽管还没有完全收敛到T*go,i。
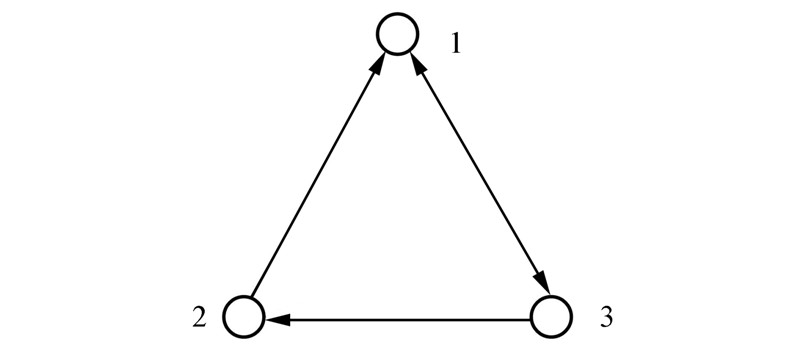 |
| 图 3 导弹通信拓扑 |
4 仿真验证
下面对该制导律进行仿真,以验证其性能。假设有3枚导弹参与协同攻击,从3个不同位置发射,要求在指定时间Td同时击中目标。假设目标静止位于(0,0)点静止不动,导弹速度大小不变。考虑到在制导过程中可能给出的导弹需用过载很大,超过可用法向过载,这时导弹将不能沿着给出的弹道飞行,因此在仿真过程中需加一个饱和模块,使导弹的法向过载在合理范围内,此处导弹加速度限制在(-5g,5g)之间。
导弹和目标的具体的参数如表 1所示。
| 导弹 |
位置/ m |
发射角/ (°) |
速度 / m·s-1 |
| 1 | (-10 000,2 500) | 35 | 330 |
| 2 | (-7 870,-4 200) | 70 | 300 |
| 3 | (-3 930,-8 210) | 120 | 290 |
这3个导弹在传统比例导引PN的作用下它们的导引时间分别是33.52、31.32、34.34 s,导引时间最大差值为3 s,导弹不能实现时间上的协同。所以要实现导引时间上的协同要采用相应的制导律。
CPN制导律的导引时间是人为事先指定的,而本文给出的基于相互通信的多导弹协同制导律是根据协调一致算法计算得出的,经计算可得Td=36.5 s,为了便于比较2种制导律,CPN的指定时间也设置为36.5 s。 不考虑导弹相互通信的情况,在CPN制导律下,导弹飞行轨迹如图 4中虚线所示。
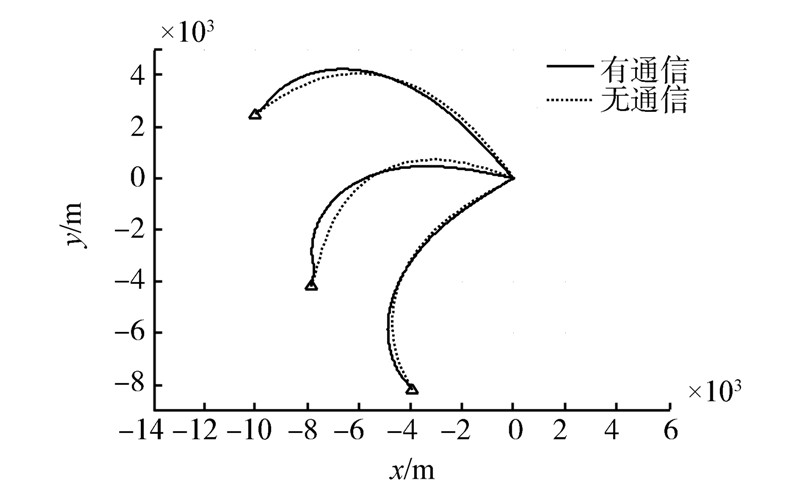 |
| 图 4 两种制导律下导弹的轨迹 |
考虑导弹之间存在相互通信的情况,使用文中提出的基于相互通信的多导弹协同制导律,弹道如图 4中实线所示。可以看出在这两种制导律作用下导弹弹道差别不大。但是CPN制导律由于导弹间没有动态的信息交互,其动态性能差,协同速度慢。如图 5所示,指定时间和剩余时间在14 s左右才趋于一致,但是在有通信情况下在4 s左右就趋于一致,实现协同的速度更快。由以上结果可以看出,基于相互通信的协同制导律协同速度快,具有良好的动态性能。
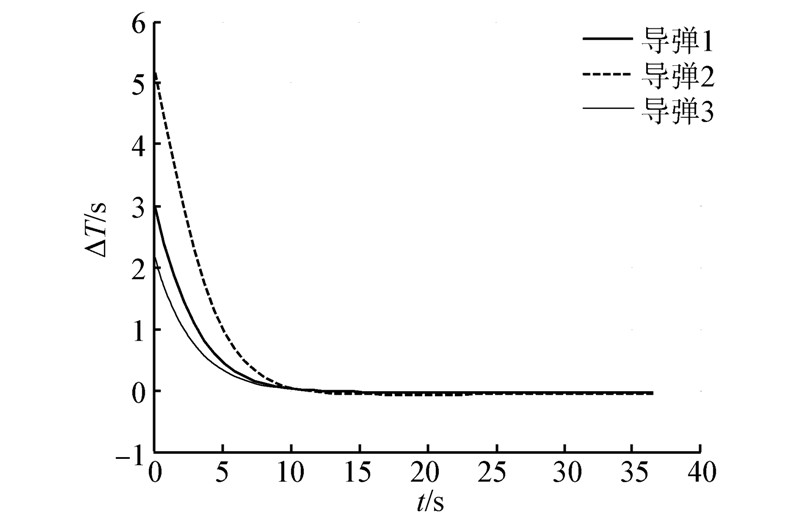 |
| 图 5 无通信情况下指定时间与剩余时间差 |
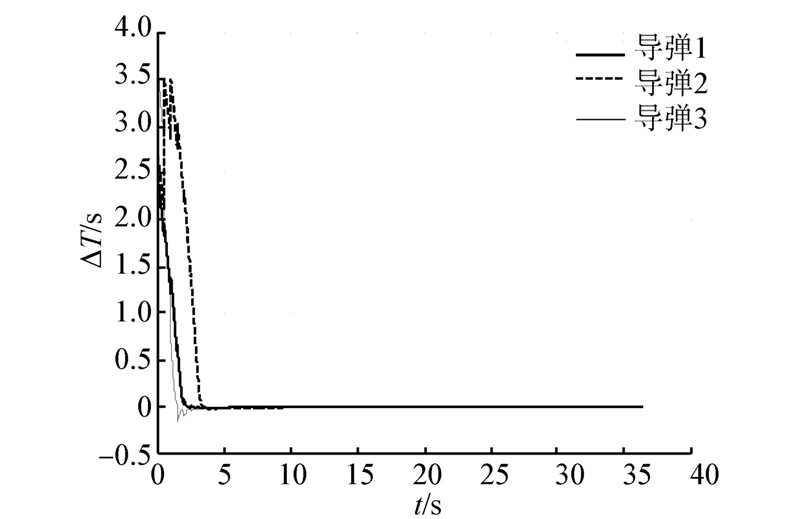 |
| 图 6 有通信情况下指定时间与剩余时间差 |
在相互通信的多导弹协同制导律作用下,导弹的剩余时间、指定时间以及弹目距离见图 7、8、9。
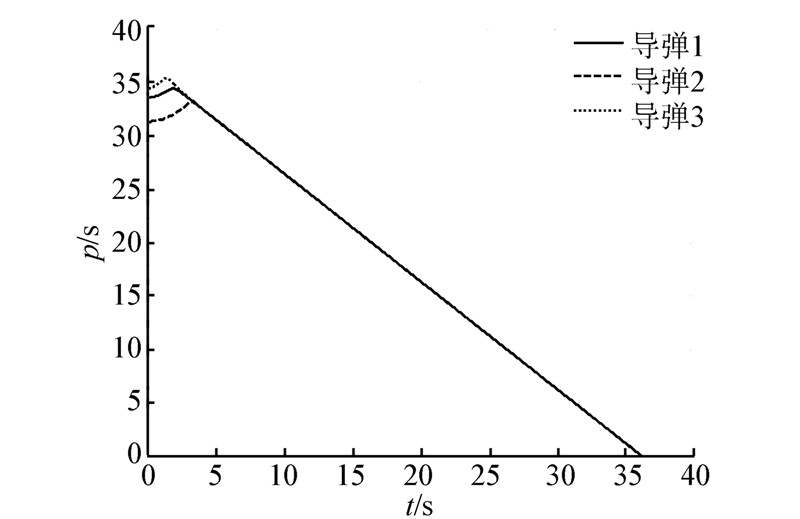 |
| 图 7 导弹剩余时间估计 |
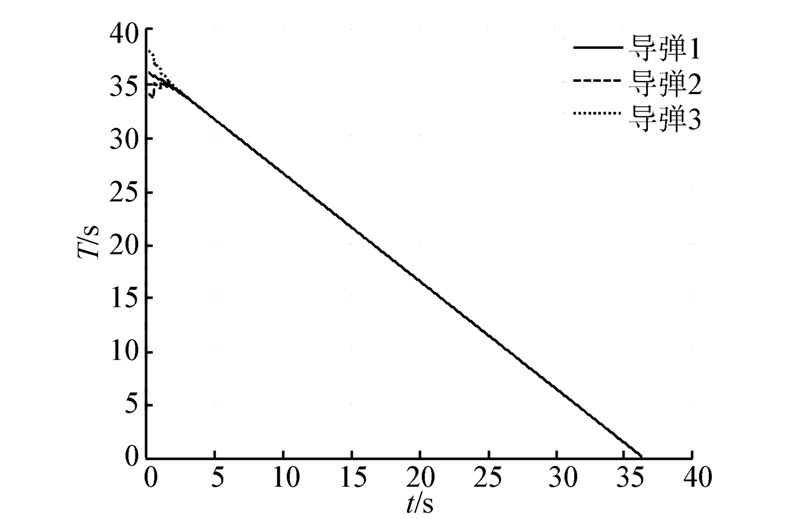 |
| 图 8 导弹指定时间变化 |
 |
| 图 9 导弹弹目距离随时间的变化 |
可以看出各个导弹的指定导引时间是分段连续的,因为一致性算法的收敛周期有限。由图 8可以看出指定时间在3 s左右就能够收敛到一致的值,表明协同速度快。
导弹加速度指令如图 10,由于加入了饱和模块,导弹法向过载在合理范围内变化。
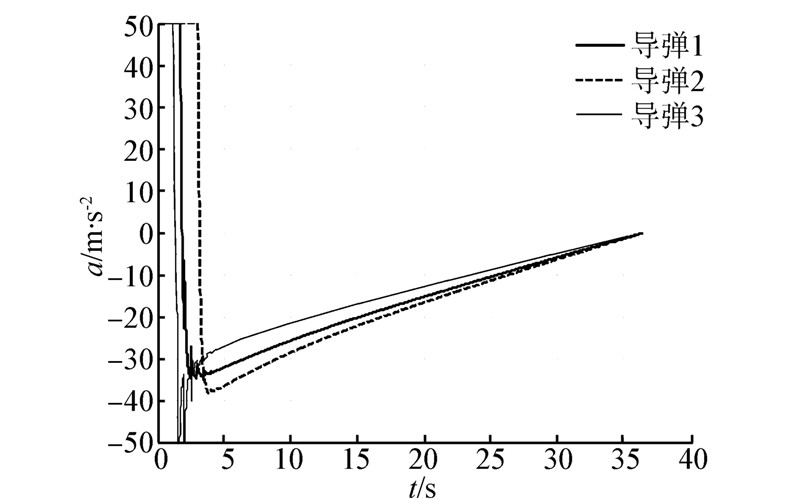 |
| 图 10 有通信情况下导弹的加速度指令 |
从以上仿真结果可以看出,本文提出的基于相互通信的多导弹协同制导律给出了解决导弹之间相互通信情况下实现协同制导的一种新的方法,并且该制导律协同速度快,动态性能好,指定时间不用事先人为设定,由协调一致算法可以计算得出。
5 结束语
为了解决导弹相互通信条件下的协同问题,本文引入了一个双层控制结构,控制层采用有时间约束的CPN制导律,下层采用了一种新型的拓扑一致性算法,通过指定时间这个变量把两层联系起来,进而给出了一种解决导弹间通信情况下实现协同的方法。通过仿真结果可以看出该制导律是可行的,并且指定导引时间不用人为事先设定,其协同速度也比无通信情况的CPN制导律快,动态性能更好。但是导弹在通信过程中会存在延迟,在本文中考虑的是理想情况并没有涉及延迟,所以有通信延迟的多导弹协同是一个值得深入研究的问题。
| [1] | 王建青, 李帆, 赵建辉, 等. 多导弹协同制导律综述[J]. 飞行力学, 2011, 29(4): 6-10. |
| [2] | 肖增博, 雷虎民, 滕江川, 等. 多导弹协同制导规律研究现状及展望[J]. 航空兵器, 2012 (6): 18-22. |
| [3] | JEON I S, LEE J I, TAHK M J. Impact-time-control guidance law for anti-ship missiles[J]. Control Systems Technology, 2006, 14(2): 260-266. |
| [4] | JEON I S, LEE J I, TA H K. Homing guidance law for cooperative attack of multiple missiles[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 275-280. |
| [5] | MARTINEZ S. UAV cooperative decision and control: challenges and practical approaches[J]. Control Systems, 2010, 30(2):104 -107. |
| [6] | NERURKAR E D, ROUMELIOTIS S I, MARTINELLI A. Distributed maximum a posteriori estimation for multi-robot cooperative localization[C]//IEEE International Conference on Robotics and Automation. Japan, 2009: 1402-1409. |
| [7] | WEI C, GUO J, CUI N. Research on the missile formation keeping optimal control for cooperative engagement[J]. Journal of Astronautics, 2010, 31(4): 1043-1044. |
| [8] | MCLAIN T W, BEATD R W. Coordination variables, coordination functions, and cooperative timing missions[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(1): 150-161. |
| [9] | BEARD R W, MCLAIN T W, NELSON D B, et al. Decentralized cooperative aerial surveillance using fixed-wing miniature UAVs[J]. Proceedings of the IEEE, 2006, 94(7): 1306-1324. |
| [10] | JIANG Jiahe. Guidance principle of missiles[M]. Beijing: Beihang University Press,2012:155-164. |
| [11] | 王海英.图论算法及其 MATLAB 实现[M]. 北京: 北京航空航天大学出版社, 2010: 1-5. |
| [12] | CHEN W K. Applied graph theory[M]. Amsterdam: Elsevier Science, 2012:3-4. |
| [13] | OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533. |
| [14] | QIN J,GAO H,ZHENG W X. Second-order consensus for multi-agent systems with switiching topology and communication delay[J]. Systems & Control Letters, 2011, 60(6): 390-397. |
| [15] | SHIYU Z, RUI Z. Cooperative guidance for multimissile salvo attack[J]. Chinese Journal of Aeronautics, 2008, 21(6): 533-539. |



