随着人们对于网络带宽、传输速度以及大容量数据交换需求的日益扩大,传统的具有组网灵活、网络覆盖率高、网络容量高、前期投入少等优势的无线Mesh网络已经不能满足现实的要求。将认知无线电(cognitive radio,CR)技术与无线Mesh网络(wireless mesh net,WMN)相结合而成的一种新型无线网络-认知无线Mesh网络(cognitive wireless mesh net,CWMN)[1],使得无线Mesh网络的节点具有在其具有认知能力、自组织能力、可重配置能力,这使得CWMN具有感知环境、分析和学习感知到的信息和适应环境的能力,从而能够更好地满足大众的需求。
频谱分配是认知无线Mesh网络中的重要研究内容,目前对于CWMN的研究仍处于初级阶段,面临许多困难与挑战。针对CWMN的频谱分配问题,大多数的研究基于线性规划的方法求解。文献[2]通过将认知无线电技术加入到无线Mesh 网络,提出了认知无线Mesh网络,提高其在资源利用率的性能。针对认知无线Mesh网络中功率分配问题,文献[3]提出了一种非合作博弈的方案。针对基于OFDMA的认知无线 Mesh 网络的资源分配问题,文献[4]提出了以最大化端到端速率为目标的资源分配的算法。针对无线Mesh中的线性规划问题,文献[5]提出了基于字典序最大最小公平性模型的解决方案,以公平性为目标,并定义了2个公平性带宽分配问题。针对多射频认知无线Mesh网络的架构问题,文献[6]提出了Urban-X这一新型构架。为使认知无线Mesh网络与其他认知无线网络能够更好地共存,以最小化占用频谱数为目标,文献[7]提出了认知无线Mesh网络中的频谱分配算法。为使Mesh客户端的数量最大化,并用线性规划方法求解频谱分配,文献[8]提出了一个基于接收器可调的频谱分配算法。文献[9]针对认知用户的动态性,提出一种基于系统效用稳定、减少频谱重分配的认知节点数的频谱分配算法,简化了动态频谱重分配的复杂度。文献[10]基于授权频谱空闲时间和认知用户请求时间的时间差,提出一种基于时间差因子的改进频谱分配算法,降低认知用户通信中断概率,提高系统稳定性。
已有的基于CWMN的研究不能在优化频谱的同时对带宽进行优化。本文基于CR-Mesh路由器以及 CR-Mesh 网关,针对感知后的可用频谱,全面考虑频谱分配时总带宽的最大化和占用频谱数的最小化;采用包括信道可用用户在相应信道的可用概率、稳定度、信道带宽这些因素进行量化;利用入侵杂草算法在较少迭代次数就显示出优于其他传统算法的优势的特点,本文针对频谱优化这一课题采用入侵杂草算法。尽管入侵杂草算法这一较新的智能算法已在传统智能算法之上有了相当大的改进,但其迭代时间较长,尤其是在一些复杂程序的问题上,基于此,本文对扩散条件进行改进,意在加快收敛速度并优化适应度函数曲线,提出IIWO算法,使得杂草算法的优势得以展现。
1 网络模型及问题描述 1.1 网络模型
在一个认知无线Mesh网络的授权信道中,随机分布着主用户PU(primary user)、次用户SU(secondary user)、 CR-Mesh路由器和CR-Mesh网关节点。每一个PU都有一个以其为中心的 1 个圆形覆盖区域。在此区域内,PU所占用的信道,SU不能使用,反之亦然。本文主要研究的是这种被称为交叉共享接入的overlay方式下的信道分配问题。
将认知无线Mesh网络建模表示为1个简单图G=(V,E)。V表示主用户集合。E表示认知网关和认知路由器。V中每个元素vi有一个感知可用信道集合Ki,Ii个可用认知射频接口,K表示总的可用信道的集合,ψi,j表示节点vi和节点vj相同的可用信道集合。 每个节点vi∈V均存在1个通信距离TR和1个干扰距离IR。在一般情况下,有3TR>IR>TR,本文假设IR=2TR。di,j表示节点vi和节点vj之间的物理距离。
E 是边的集合,表示网络中的两节点有公共可用信道的情况下,是否可直接进行传输,ei,j=1表示di,j≤TR,相反,ei,j=0表示di,j≥TR。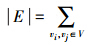 ei,j/2,表示图G中边的条数。
ei,j/2,表示图G中边的条数。
所有节点假设采用半双工方式工作,存在一个公共信道,并且假设存在一个频谱分配服务器负责为CR-Mesh节点分配频谱。
1.2 问题描述
主用户的频谱只有空闲与占用2种状态,在相同考察时间内,在频谱占用率相同情况下,跳表次数多的情况稳定度不高;稳定度相同(即跳变次数相同)情况下,频谱占用率与主用户可用性成正比,而与次用户的可用性成反比。
因而在这里,考虑2个参量:
1)频谱占用度Pi。即每个主用户在相应信道上的可用概率。在算法中可以用一个M×N阶可用概率矩阵表示,M表示主用户数量,N表示考察时间个数,矩阵中的元素为0或者1,为0时,表示此主用户在相应信道上是不可用的,表示为E(p)=0,p为相应考察时间内所考察的信道;为1时,表示其在相同信道上是可用的,表示为E(p)=1可用概率计算方法如式(1):
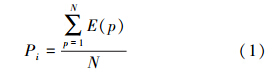
2) 信道稳定度Si(i表示某个考察主用户)。即主用户在考察信道上的由空闲跳变到占用的跳变(即由0~1)次数Hi(i表示某个考察主用户)。信道占用率体现的是此用户在考察期间保持信道占用的稳定程度。信道占用率定义如式(2):
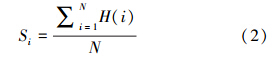
2.1 基本入侵杂草算法
入侵性杂草优化算法(invasive weed optimization,IWO)是伊朗德黑兰大学的A.R.Mehrabian和C.Lucas[1]受杂草启发而首次提出的一种基于种群的数值优化计算方法,广泛应用于模式识别、自动控制、机械设计、数据挖掘、决策分析等诸多领域。入侵杂草优化算法的基本步骤主要有4个步骤:
1)初始化杂草种群
设置种群个体数、最大种群个体数、迭代次数、所要解决的问题维数、最大种子数、最小种子数、调和指数、方差的最大值和最小值、问题解的最大最小范围。
2)种子的生长和繁殖
产生杂草种群的种子,种子数量如公式(3):
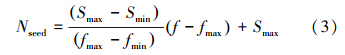
3)种子的空间扩散
对于每个个体产生的所有种子,按照其父代为基准(也就是均值),产生正态分布随机数以正态分布的方式将种子扩散到维空间中去,标准差的更新公式如式(4):
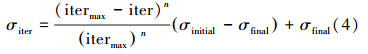
4)竞争排除
每次生长完成后都要将适应度函数值最差的个体去除,保持种群大小不变。
2.2 改进策略
用动态标准差作为更新的步长,是杂草算法区别于其他算法的优势所在,σiter伴随着迭代次数iter发生改变,算法的前期和中期,对优秀个体周围的空间搜索频率较快,以防陷入局部最小值;到了后期,随着iter的增加,σiter愈来愈小,搜索的范围愈缩愈缩小,有利于提高算法的精度,找到最优解。但在以往传统的入侵杂草算法中的n是固定不变的,通常设定为一个常数,这使得σiter在每次更新时的动态可扩展性不强,没有充分发挥其在收敛问题上的优势,本文对于n做了相应调整,使其按照式(5)、(6)进行更新调整。

本文设置n的初值为Xmax/15(Xmax为搜索范围的最大值),nmin=0.03,iter为当前迭代次数,S范围为[1, 15]。
2.3 适应度函数
本文主要研究以最大化总带宽和最小化占用频谱数的情况下,以较快的收敛速度找到适应度函数的最优解。对任意粒子i,定义其适应度函数为F(i),如式(9)。总带宽B指的是所有 CR-Mesh 节点获得的带宽总和。其中E(li,j)表示信道是否分配无线链路li,j。记b1表示无线链路li,j在信道的带宽,其大小是由信道的特征决定的,一般取0~10之间的数。Si表示某考察用户的频谱稳定度;Pi表示频谱占用率。H表示为频谱占用次数,θ(i)表示所有考察时间内的0的个数。粒子的适应度值越大,表示其被选中的可能性越大,本文的目标是希望找到适应度值最大的粒子。

1)初始化种群,对调和指数按式(5)、(6)进行优化,对其他相关实验参数进行设定。
2)按照式(6)~(9)计算初始种群适应度函数f(i),对其升序排列。
3)按照式(3)计算每个个体能产生的种子数。
4)产生新个体,与父代相加,组成新种群,若新种群超出设定的最大种群个体数,则去除适应度函数较小的且超出种群限定范围的个体,否则跳到5);
5)若达到最大迭代次数,算法终止,否则回到步骤2)继续执行算法。
3 性能仿真及结果分析
实验采用MATLAB R2010a软件进行仿真,在Intel(R) Celeron(R) CPU 2.60 GHz,2 GB内存,Windows Xp系统的计算机上运行。采用PSO和改进IIWO的方法对本实验进行仿真对比。
假设仿真的网络拓扑结构为某高校的校园网,在2 500 m×2 500 m的区域,存在若干主用户以及若干可用信道,主用户随机的占用这些可用信道。在该区域部署着具有认知能力的 Mesh 路由器。Mesh路由器节点的传输范围为50 m,并且均匀部署在区域内。
以下实验结果均为50次独立仿真结果的均值。性能的比较主要包括系统总带宽、占用的信道数目2个方面,占用信道数越多,表示其他认知无线网络可用的信道数越少。假设各信道的带宽属于[0,10],并且随机产生,考察信道带宽b随机产生,取值在0~10之间;主认知用户数为6,可用频带数为8。
实验主要由以下2方面进行仿真:
1)对参数a,b、节点数N和可用信道数K进行分析仿真,得到使得算法性能最佳的值。
2)使用在1)中得到的参数数值,对调和指数的改进进行仿真对比,对迭代时间进行记录,得出结论。
3.1 参数对算法性能的影响分析
根据文献[12]对于参数a,b的描述,设定a=0.6,b=0.4。
1)可用信道数|K|对基于IIWO算法的性能影响。用户数M的范围为[21,51],间隔为10,频谱数N的范围为[1,M]。K取值范围设为[0,30],迭代4次。
由图 1可知,随着K值的增大,目标函数值随之增大,但是并不随着M,N的增大而增大,由图可知当M,N在取值范围[31,41]之间时目标函数曲线较为理想。
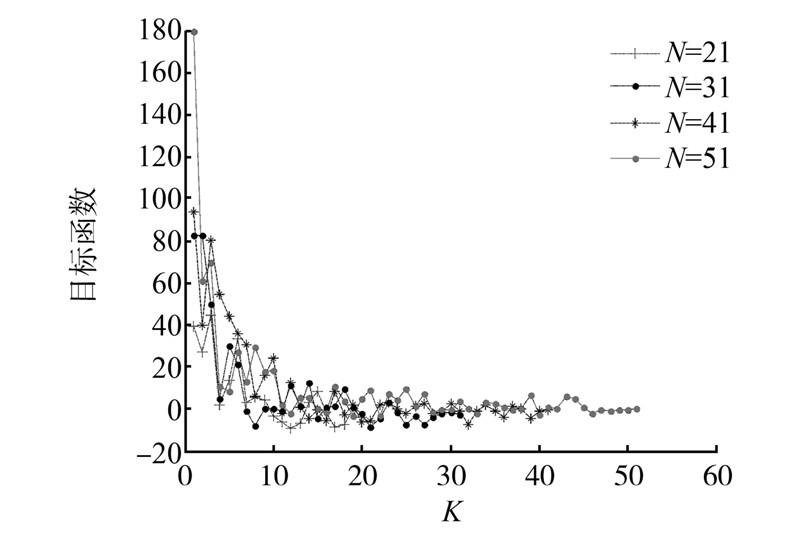 |
| 图 1 可用信道数K与目标函数的关系 |
2)可用频谱数N对基于IIWO算法的性能影响。可用信道数|K|=10,a=0.6,b=0.4,M取值35,N取值范围为[1, 50],图迭代50次。分别仿真了变量N对总带宽曲线和信道占用数曲线的影响,仿真图如图 2、3。
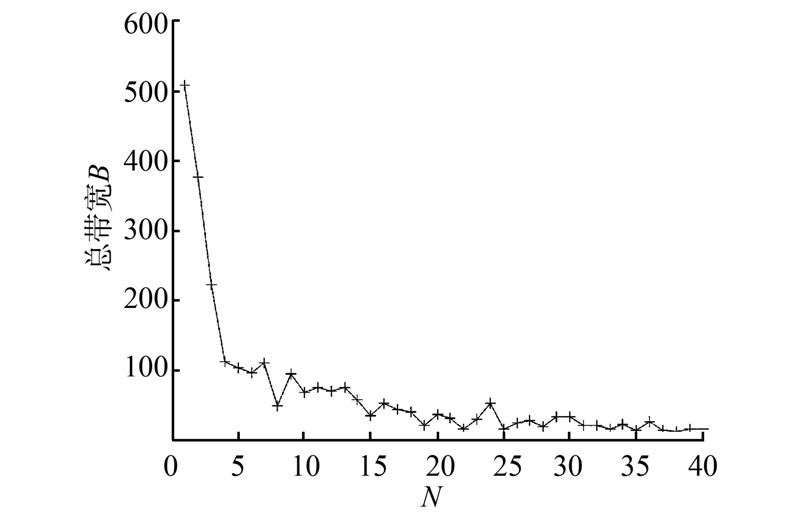 |
| 图 2 种群大小N与总带宽B的关系 |
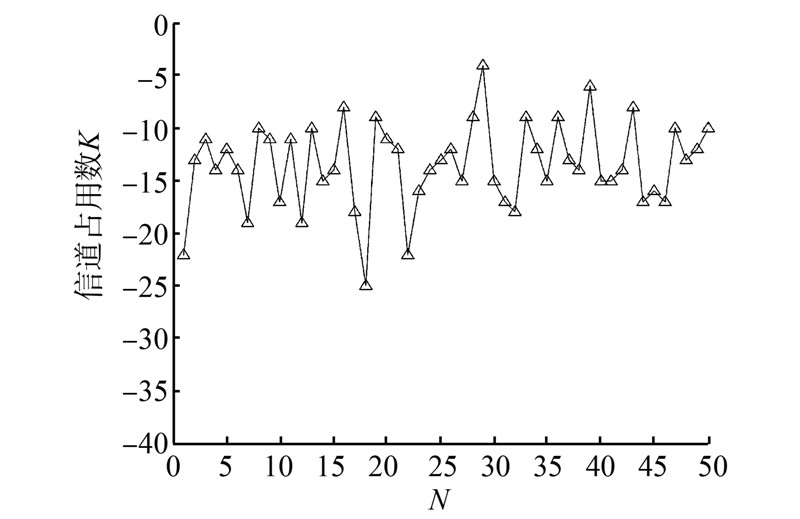 |
| 图 3 种群大小N与信道占用数K关系 |
由图 2可知,随着N增大,总带宽变大,并有缓慢下降的趋势。由图 3可知,N在0~25之间时,信道占用数基本不变,并且震荡较不稳定,且有下降趋势;N在25~50之间时,信道占用数曲线较理想,趋于平衡。
3.2 改进算法的优化结果
在调和指数按照式(5)、(6)改进后,所得适应度函数值随迭代次数的变化曲线与应用粒子群算法的适应度函数曲线图的对比如图 4所示。改进前算法收敛时间为1.259 088 s,改进后,算法收敛速度为1.082 003 s,最优值为0.802 311。由此可见,基于改进的IIWO算法确实加快了算法的收敛速度,曲线也得到了有效改善。
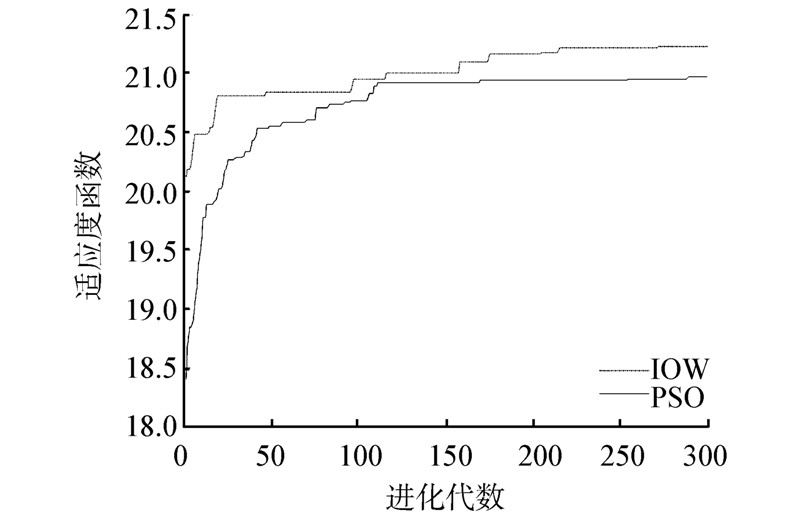 |
| 图 4 适应度函数最优值与迭代次数的关系 |
4 结论
1)利用IWO算法种群多样化的优势,提出了基于IIWO的网络优化频谱分配算法。综合考虑同时获得最大系统总带宽和最小化占用信道数的情况下,对调和函数进行改进,有效提高了算法的收敛速度,并获得较为理想的目标函数曲线。
2) 通过合理的参数设置,在获得高的系统总带宽和较少频谱占用数的情况下,通过改进杂草算法和粒子群算法对方案的实现进行对比,本文所提出的IIWO算法对适应度函数有明显的改进。
因此,采用本文提出的IIWO算法在保证高的系统总带宽并且占用较少频谱的情况下,同时达到了加快收敛速度和改善适应度曲线的效果。
| [1] | 仵国锋, 季仲梅, 张静, 等. 认知无线 Mesh 网络[J]. 信息工程大学学报, 2010, 11(4): 429-433. |
| [2] | LEE D H, JEON W S, JEONG D G. Joint channel assignment androuting in cognitive radio-based wireless meshnetworks[C]//IEEE Vehicular Technology Conference. Ottawa,Canada, 2010: 1-5. |
| [3] | ZHANG Jianmin, ZHANG Zhaoyang, LUO Haiyan. Jointsubchannel, rate and power allocateion in OFDMA-basedcognitive wireless mesh network[J]. Wireless Personal Communications, 2009, 58(3): 1478-1487. |
| [4] | AlMASAEID H M, KAMAL A E. Receiver-based channel allocation for wireless cognitive radio mesh networks[C]//2010 IEEE Symposium on New Frontiers in Dynamic Spectrum, DYSPAN2010. Singapore, 2010: 1-5. |
| [5] | TANG Jian, HINCAPIé R, XUE Guoliang, et al. Fair bandwidth allocation in wireless mesh networks with cognitive radios[J]. IEEE Transactions on Vehicular Technology, 2010, 59(3):1487-1496. |
| [6] | WOOSEONG K, KASSLER A K, DI F M, et al. Urban-X: towards distributed channel assignment in cognitive multi-radio mesh networks[C]//2010 IFIP Wireless Days., 2010: 1-5. |
| [7] | YONG Ding, LI Xiao. Channel allocation in multi-channel wireless mesh networks [J]. Computer Communications, 2011,34(7): 803-815. |
| [8] | BOUABDALLAH N, ISHIBASHI B, BOUTABA R. Performance of cognitive radio-based wireless mesh networks[J]. IEEE Transactions on Mobile Computing, 2011, 10(1): 122-135. |
| [9] | 李一兵,杨蕊,高振国.基于着色理论的认知无线电频谱分配算法[J]. 系统工程与电子技术,2010,32(6):1109-1112. |
| [10] | 文凯,傅小玲,付玲生.认知无线电中基于时间差因子的频谱分配算法[J]. 计算机应用, 2011, 31(5): 1173-1175. |
| [11] | MITOLA J. Cognitive radio: making software radio more personal[J]. IEEE Personal Commnuication, 1999, 6(4): 13-18. |
| [12] | 邝祝芳.认知无线Mesh网络中一种有效的多目标优化频谱分配算法》[J]. 中南大学学报, 2013(6): 73-75. |



