2. 北京离子探针中心, 北京 100037;
3. 中国地质科学院地质研究所, 北京 100037
2. Beijing SHRIMP Center, Beijing 100037, China;
3. Institute of Geology, Chinese Academy of Geological Sciences, Beijing 100037, China
锆石U-Pb测年法是放射测年法中最早使用且准确度最高的测年方式,可测定距今100万年到45亿年的地质体年代,厘定精确度大约是测定范围的1%至10%,被广泛运用到地质科学研究中(Rino et al., 2004; Iizuka et al., 2005;Condie et al., 2009, 2017; Condie and Aster, 2010;Bahlburg and Berndt, 2016)。近20年来,中国大陆地壳锆石U-Pb年代学发表相关论文数量最多、增长最快。通过收集单颗粒锆石U-Pb年代学数据,建成中国大陆地壳单颗粒锆石U-Pb年代学数据库十分有必要。中国大陆地壳单颗粒锆石U-Pb年代学数据库能够在大范围内为认识中国大陆地壳形成演化提供更完整和系统的科学信息,一定程度帮助讨论解决许多有争议的基础地质问题,如大陆地壳形成的阶段性、大陆地块的分区、锆石生长与大陆地壳生长的关系、地壳从地幔中的分异形式和过程、大陆演化中气候与构造的关系等地球动力学方面的重要科学问题。
国内外学者在研究不同的科学命题时,注意到了锆石U-Pb年代学数据的意义。河砂中碎屑锆石的年龄分布代表的大陆地壳生长(Rino et al., 2004; Iizuka et al., 2005)、岩浆锆石与碎屑锆石反映的花岗岩事件的时空分布(Condie et al., 2009; Condie and Aster, 2010)等研究建立了锆石U-Pb年代学数据库,关于锆石生长峰期与大陆地壳之间的关系还在持续讨论中(Bahlburg and Berndt, 2016; Condie et al., 2017)。同时,有学者已经从建立锆石U-Pb年代学数据库的角度去分析测年方法优劣等相关问题(Puetz et al., 2018)。
1 数据库建设 1.1 数据来源中国大陆地壳锆石U-Pb年代学数据子库的数据源是截至2017年底中国知网上收录的含有“锆石”、“U-Pb”等关键词的约4000余篇中文期刊与学位论文,最终拥有有效数据的共2331篇。文献均被收录于对应文献库中,且文献库中的文献编号与数据库中的文献编号项对应。在经过数据录入和两轮数据检查后,现今数据条目数为154768条。相关数据库可以通过邮件联系本文第一或通讯作者获取。
1.2 数据库结构数据库基于Access建立,有41个锆石年代学及相关信息的数据项。
每个样品测试点的U、Th元素与同位素含量、同位素比值及误差、年龄及误差以及实验技术背景等数据项均被采集,编入数据库中。在锆石年代学分析中,样品的信息很重要,测试方法也一定程度影响结果的精度,而测试数据如同位素比值及其误差、年龄及其误差则是锆石年代学分析的主体。此外,循着数据能找到数据源及数据录入责任人,用以保证数据库建设质量。数据库的数据项按其类别主要分为4部分:
(1) 样品背景:包括样品测试号、样品岩性、样品采集位置(包括GPS与地名)等;
(2) 技术背景:包括测试方法、标样、标样的备注;
(3) 测试数据:包括Pb、U、Th等的含量、Th/U、同位素比值及误差、年龄及误差,另外某些测试数据在其他补充项中;
(4) 文献录入情况:包括文献编号、录入人、检查人、负责人等。在数据库建设过程中,每一数据项都有相应的录入规则以及问题解决方案。每一内容项的具体说明见表 1。
|
|
表 1 数据项描述、问题与解决策略 Table 1 Data item description, problem and solution strategy |
锆石U-Pb年龄数据的测试方法主要包括LA-ICP-MS(包括LA-MC-ICP-MS、MC-ICP-MS和ICP-MS等)、SHRIMP(包括SHRIMP Ⅱ和SHRIMP RG等)、SIMS(指Cameca IMS系列),以及TIMS等4种。其中,LA-ICP-MS法获得的数据共132865条;SHRIMP法获得的数据共17991条;SIMS法获得的数据共2814条;TIMS法获得的数据仅有331条,文中不予讨论。由于年龄误差能反映不同测试方法、不同年龄值的精确度,而且可以帮助判定数据质量以及与测试处理可靠性。针对不同的测试方法,分别对锆石的206Pb/238U年龄、207Pb/235U年龄、207Pb/206Pb年龄和208Pb/232Th年龄这4个年龄及其误差的相关性进行了分析。
2.1.1 数据处理根据放射性核素衰变原理,放射成因子体与剩余放射性母体的比值(以下简称“同位素比值”,用x表示)与年龄(用t表示)是一一对应的函数关系。同位素比值的变化会引起年龄的变化。实践经验和理论分析表明,测量误差可以看作服从或近似服从正态分布,而某测试点的同位素是锆石同一位置多次分析测试得到的结果,其标准差可以近似看作服从正态分布。同位素比值标准差则是两种不同μ的正态分布的比值做一定调整的结果,其也服从一定的概率函数分布。测试获得的同位素比值标准差是其分布的均值很好的估计量。分析测试的次数越多,则估计效果越好。年龄与同位素比值是函数关系,若将dx近似看作Δx,dt近似看作Δt,则在同位素比值确定、从而确定年龄的情况下,dx与dt成线性关系,也即dt与dx同分布。
在以上理论基础上,每个年龄应该对应一个年龄误差区间,且其服从一定的概率函数分布。年龄-年龄误差散点图的投图研究可以提供对每个年龄对应的误差区间的一定信息,但是未处理的数据库中的原始数据难以对数据整体做更深的研究。
对原始数据进行处理包括选择不同的区间长度,对区间内的数据点进行分析,再将所有区间拢合进行整体性研究。区间长度的选择尝试包括5Ma、10Ma、20Ma、50Ma、100Ma等。不同区间长度决定着不同的年代学研究精度,当区间长度足够小时,可以认为区间内的年龄仅对应同一概率函数分布。理论上来说,区间内所有的数据都应该保留,样本才能有效反映总体的特点。但是由于数据点数目(n)较小,概率函数分布两端的数据会对样本均值产生巨大影响,所以在确定区间长度的基础上,采用箱线图法(Williamson et al., 1989)对每个区间内的年龄-年龄误差点进行判断去除极端值点。具体方法是将处在某区间内的所有年龄值所对应的误差值按从小到大排列,取排列在25%到75%间的数据,认为其为正常值,设其长度为IQR,在25%到75%之外1.5IQR区间内的数据也被视为正常值,其余的则被作为异常点去除。箱线图法是总结与比较数据群的很好方法,能提高对数据群的理解与认识。
在对每个区间进行去除异常点后,采用每个区间内年龄所对应的误差的平均,赋予区间中值年龄的方法进行投图。样本的均值是总体均值很好的估计量。它不但能在一定程度上表明趋势变化,还能反映年龄与对应年龄误差分布之间的关系。在比较不同的区间长度的投图结果后,确认解析度较好的5Ma为所使用的区间长度。
2.1.2 拟合函数选择年龄-平均误差散点图的拟合函数并不能简单用线性、多项式、指数函数等进行拟合。除了观察散点图中散点的分布趋势以外,还需要与理论方面进行结合。
在锆石U-Pb测年中,每个测试点的同位素比值其实是在锆石的同一位置上测试若干次所得的平均值,而同位素比值的1σ误差则是这些点的标准差做了一些校正的计算后的结果。由于实验室计算同位素比值误差的时候会根据一些经验规则去除原始数据的离群点,所以最终文献中的误差值会掺杂些许人为因素。以SHRIMP为例(宋彪等,2015),实验仪器所得的数据要先去除离群点,然后再根据标样的(Pb/U)/(UO/U)2计算待测样品的同位素比值及其误差,还要根据204Pb、207Pb、208Pb进行校正。得到的同位素比值数据再用SQUID进行计算,得到最终的年龄及其误差。此外,年龄误差的计算还用了一些经验规则。
由于影响因素过多,年龄误差与年龄之间在理论上并没有严格的对应关系。通过所有测试点的年龄-年龄误差散点图可以看出,每个年龄对应的是一个年龄误差区间,而不是某个值,但仍然可以发现年龄误差随年龄变化有一定趋势。为找到这个变化趋势,仍采取对一个年龄区间内的年龄误差取平均值的方式,以年龄、年龄误差分别为横坐标、纵坐标投散点图,进行曲线拟合。
根据同位素定年原理:
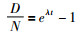
|
(1) |
其中D为衰变的原子核数,N为剩余的衰变原子核数,λ为衰变常数,t为衰变时间。
取微分得:
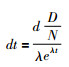
|
(2) |
若只考虑dt是t的函数,忽略其他因素,根据同位素定年原理,可以得到:
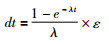
|
(3) |
其中,ε表示同位素比值的相对误差(dx/x),同位素比值分别对应206Pb/238U、207Pb/235U、208Pb/232U。
而对于207Pb/206Pb,则有:

|
(4) |
其中λ75表示235U衰变为207Pb的衰变常数,λ68表示238U衰变为206Pb的衰变常数。
取微分得:
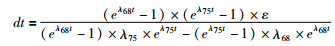
|
(5) |
其中ε表示同位素比值的相对误差(dx/x),同位素比值对应207Pb/206Pb。
选择公式(3)、(5)所对应的形式分别对4个年龄-年龄误差散点图进行拟合,选择的公式及拟合情况如下:
根据公式(3)的形式选用BoxLucas1函数:
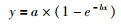
|
(6) |
根据公式(5)的形式得到:

|
(7) |
用(6)对Age(206Pb/238U)、Age(207Pb/235U)、Age(208Pb/232U)的绝对误差进行拟合,而不进行迭代,所有测试方法的数据的R2分别为90.1%、70.6%、57.5%。用(7)对Age(207Pb/206Pb)的绝对误差进行拟合,所有测试方法的数据的R2为53.7%。拟合结果显示,前3个年龄的年龄值在影响年龄误差的因素中占有较重要地位,而对于Age(207Pb/206Pb)所对应的年龄误差,年龄值对其影响却有限。对于Age(207Pb/206Pb),在目前理论探索仍待进一步研究的情形下,使用多种尝试与观测,确认Log3P1函数为:
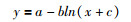
|
(8) |
对Age(207Pb/206Pb)的拟合优度较佳,R2达到了78.2%。
为了验证此次拟合结果对Age(206Pb/238U)、Age(207Pb/235U)、Age(208Pb/232U)的合理性与Age(207Pb/206Pb)拟合较差的情况,计算出每条数据的同位素比值的相对误差作为(3)与(5)式中的ε进行年龄理论误差的推算,并与数据库中实际的年龄误差进行对比。取每条数据中每个年龄基于上述公式计算出的“理论误差”与实际年龄误差间的差值绝对值,称其为“相对偏差”。再计算相对偏差与实际误差的比值,称其为“相对偏差比值”。计算如(9)式:

|
(9) |
对相对偏差比值做统计,分析结果显示,Age(206Pb/238U)、Age(207Pb/235U)、Age(208Pb/232Th)在10%以内的相对偏差比值的数据占总数据的比例分别为71%,80%,74%,进一步验证了选取BoxLucas1函数进行拟合的合理性。另一方面,根据(5)式得出的Age(207Pb/206Pb)的“理论误差”,仅有31%的数据的相对偏差比值在10%以内,这也解释了(7)式的低拟合优度现象。由此可以推出,同位素比值207Pb/206Pb的误差的变化可能也很大程度地影响了Age(207Pb/206Pb)的误差,以致不能简单地只考虑年龄对年龄误差的影响。
2.1.3 拟合结果与讨论最终选择用BoxLucas1函数对Age(206Pb/238U)、Age(207Pb/235U)、Age(208Pb/232Th)进行拟合,用Log3P1函数对Age(207Pb/206Pb)进行拟合。拟合采用一次迭代的方法。具体方式是选用函数对数据进行拟合,去掉第一次拟合结果中残差绝对值最大的10%的数据。剩余数据再次进行拟合,总体的拟合结果较好。拟合函数的具体参数见表 2。3种测试方法与所有测试方法的4个年龄拟合结果见图 1、图 2。
|
|
表 2 不同方法的数据拟合函数参数 Table 2 Data fitting function parameters of various methods |
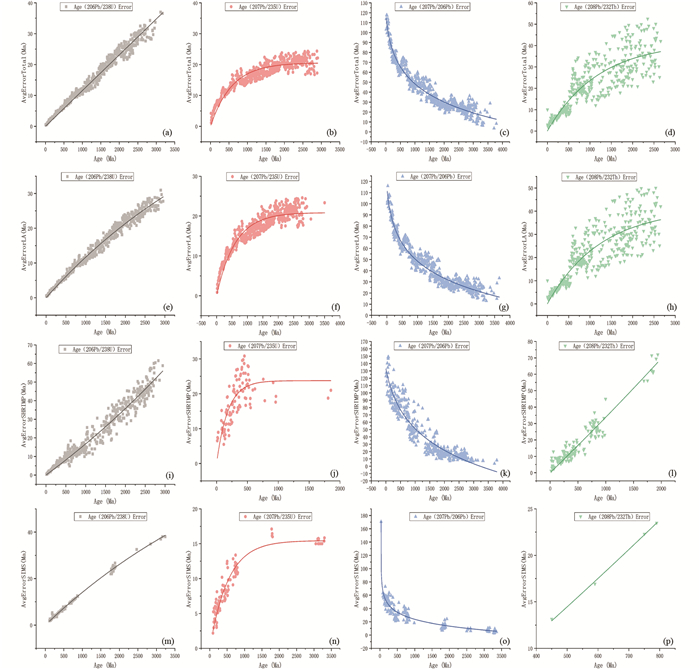
|
图 1 不同方法的4个年龄-年龄误差的散点图与拟合曲线 所有方法的Age(206Pb/238U)(a)、Age(207Pb/235U)(b)、Age(207Pb/206Pb)(c)和Age(208Pb/232Th)(d);LA-ICP-MS的Age(206Pb/238U)(e)、Age(207Pb/235U)(f)、Age(207Pb/206Pb)(g)和Age(208Pb/232U)(h);SHRIMP的Age(206Pb/238U)(i)、Age(207Pb/235U)(j)、Age(207Pb/206Pb)(k)和Age(208Pb/232Th)(l);SIMS的Age(206Pb/238U)(m)、Age(207Pb/235U)(n)、Age(207Pb/206Pb)(o)和Age(208Pb/232Th)(p) Fig. 1 The scatter plots and fitting curves of averaged absolute errors for various methods |
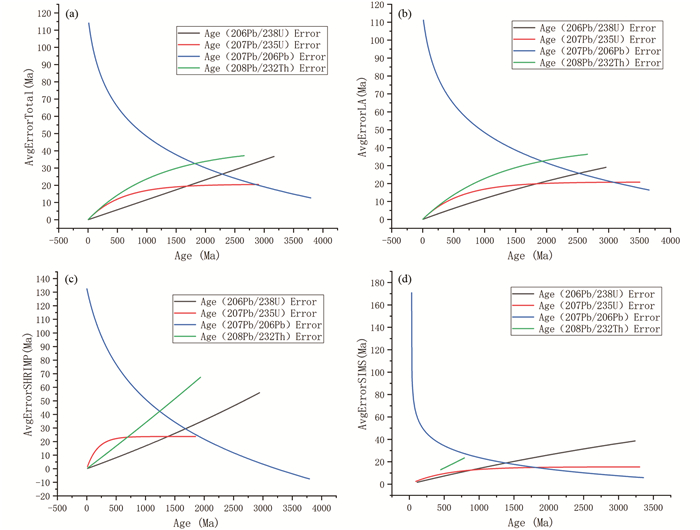
|
图 2 所有方法及三种测试方法的拟合曲线结果 (a)所有方法的拟合曲线;(b)LA-ICP-MS的拟合曲线;(c)SHRIMP的拟合曲线;(d)SIMS的拟合曲线 Fig. 2 Results of fitting curves for all methods and three test methods |
需要指出的是,含量是影响同位素比值误差的重要因素。一般来说,元素含量越低,越难测准,同位素比值误差越大。而根据(2)式,在其他因素一定的情况下,同位素比值误差越大,年龄误差越大。将同位素比值的相对误差视为定值,也即忽略元素含量对年龄误差的影响,进行年龄值-年龄误差的讨论只有在数据量较大时才有一定意义。统计方法强调数据的整体性。但是忽略元素含量对年龄误差的影响也不总是成功的,如Age(207Pb/206Pb)与其误差关系的讨论中,(7)式对数据的拟合就不尽人意。因此,探究年龄-年龄误差关系仅仅提供了比较年龄精确度的一个方向。
2.2 推荐年龄在年龄相同时,年龄误差小意味着其精度高,所以在Age(206Pb/238U)、Age(207Pb/235U)、Age(207Pb/206Pb)选用年龄误差较小的年龄作为该年龄区间的推荐年龄是合理的。
因此根据年龄-年龄误差图拟合曲线的相互关系,可选择出每个年龄区间的推荐年龄。所有方法、LA-ICP-MS、SHRIMP、SIMS等4种情形选择出的推荐年龄具体的分界点有较大区别,但总体的顺序都是一致的(表 3):较小年龄选择Age(206Pb/238U),中间年龄选择Age(207Pb/235U),较大年龄选择Age(207Pb/206Pb)。
|
|
表 3 推荐年龄 Table 3 The recommended age |
本文的推荐年龄仅仅是从年龄精确度角度分析的结果。如果结合自然界U-Pb同位素的特点、测试过程等,上述推荐年龄的选择还存在诸多问题。问题之一是:是否选用Age(207Pb/235U)。一般来说,206Pb含量远大于207Pb含量,238U含量远大于235U含量,这样就使得206Pb/238U的相对误差远小于207Pb/235U的相对误差。就测定而言,目前自然界的238U/235U(原子个数比)=137.88,尚未发现有U同位素分馏,故通常仅测定238U而不测235U,所以一般不取Age(207Pb/235U)。问题之二是:对于较老的样品,无论207Pb/206Pb比值的相对误差大小如何,只要有铅丢失,就应该使用207Pb/206Pb年龄,即选择年龄时,准确度应优于精确度考虑。
推荐年龄的应用广泛。它提供了一种整合测年结果的方法。在选择推荐年龄的基础上,可以比较不同测试方法的优劣,也可以进行年龄-频数图的探究。相较于分别使用Age(206Pb/238U)、Age(207Pb/235U)、Age(207Pb/206Pb)、Age(208Pb/232Th)4个年龄进行分析,推荐年龄更有代表性。
2.3 三种测试方法的比较锆石U-Pb年代学发展迅速,测试方法也有很多。目前单颗粒锆石及微区定年方法主要有SHRIMP、SIMS、LA-ICP-MS、TIMS等,但中文文献库中TIMS的数据较少,不足以进行单独分析,所以测试方法的比较研究并没有包括TIMS。学界对这几种方法的精度有不同的认识,主要是基于测试原理与测试仪器以及经验的认识。在选择了推荐年龄的基础上,进行3种测试方法的年龄-年龄绝对误差分析,可以从数据误差的角度对3种方法的精度有一认识。
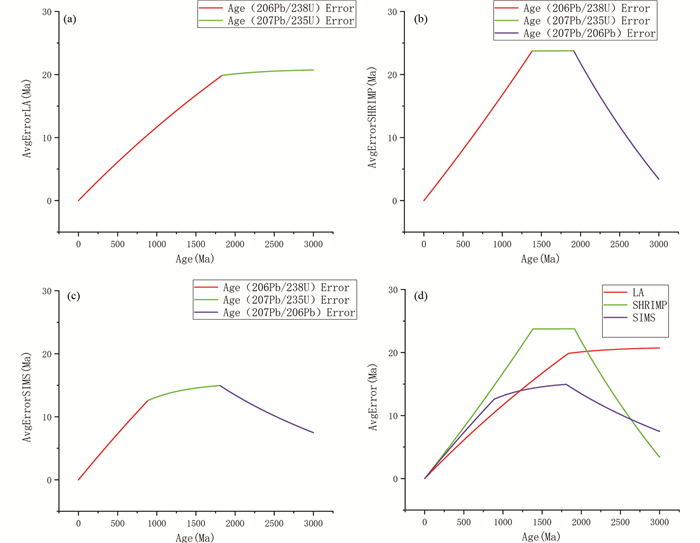
对于LA-ICP-MS、SHRIMP、SIMS等3种测试方法,绘制推荐年龄选择规则下的年龄-年龄误差拟合曲线图,三种方法的曲线图均为分段函数。按绘制结果(图 3),12亿年以来选用LA-ICP-MS较合适,元古代至约12亿年前选择SIMS,太古代及以前选择SHRIMP较合适。实际上,锆石年代学测试时一些人为因素的干扰、取样量、剥蚀深度等因素会影响不同测试方法得到的锆石年龄误差。如LA-ICP-MS远大于SHRIMP方法的取样量,相应地前者的年龄误差会较小。但是当锆石不均匀时,LA-ICP-MS的剥蚀深度过深可能会对测定结果造成不利影响。所以上述根据年龄误差进行的3种测试方法的比较仅仅是从数据讨论的结果,在指导测试方法的选择上的作用还很有限。
|
图 3 三种测试方法的年龄-年龄误差误差拟合曲线图 横坐标为年龄,纵坐标为区间平均年龄误差.(a)LA-ICP-MS;(b)SHRIMP;(c)SIMS;(d)三种测试方法 Fig. 3 Age-age error fitting curves of three test methods |
由于不谐和年龄可能对有确定意义的数据统计工作形成干扰,所以本文通过选择谐和年龄进行年龄-频数图的统计,来减少异常点对结果的影响。为实现谐和致年龄从全体数据中区分出来的目的,设计了谐和年龄计算的规则。Age(206Pb/238U)、Age(207Pb/235U)、Age(207Pb/206Pb)3个年龄,如果某条数据仅有1个年龄,则舍去;如果仅有2个年龄,若它们在误差范围内一致,则此年龄为谐和年龄;如果有3个年龄,则要求3个年龄在误差范围内一致才算一致。本文经过清洗的154768条年龄数据中,通过谐和年龄检验的数据共有72513条。
3.2 锆石年龄-频数图年龄-频数图的科学意义探索,可以分为两个方向。其一,选用不同的区间长度,包括5Ma、10Ma、20Ma、50Ma、100Ma。不同区间长度,解析度不一样,区间长度越小,则所观测到的年龄概率分布的个数就越多且越清晰。在比较了各个区间长度所显示的解析度后,选择5Ma作为使用的区间长度。其二,是选择哪一个年龄作为分析年龄。Age(206Pb/238U)、Age(207Pb/235U)、Age(207Pb/206Pb)、Age(208Pb/232Th)4个年龄的年龄-频数的统计分析,发现使用一致年龄与使用包括不一致在内所有年龄数据,前3个年龄统计的趋势是一致的,只不过选用一致年龄的数据比选用所有年龄的数据的波峰波谷更清晰,这也证明了选用一致年龄的科学性。
4个年龄的分别投图并不能有效全面地表现锆石年龄的真正分布。前文的研究中所得出的推荐年龄则提供了一条更为合理的途径。在小于1684.4Ma的年龄范围内,选择Age(206Pb/238U),在1684.4~2855.2Ma的年龄范围内,选择Age(207Pb/235U),在大于2855.2Ma的年龄范围内,选择Age(207Pb/206Pb)来进行年龄-频数投图。
使用5Ma为区间长度、一致年龄为数据源、推荐年龄为年龄选择的年龄-频数统计图中可见明显的6个锆石生长峰期。
3.3 高斯多峰拟合(Gaussian Multi-Peak Fitting)使用Gauss模型(Guo, 2011)对年龄-频数柱状图做多峰拟合以探讨峰期情况。其中拟合函数:
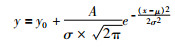
|
(10) |
(10) 式对应锆石年龄-频数图的拟合,则y为频数,x为年龄,μ为概率分布的期望,即峰值,对应年龄则可说峰期;σ为概率分布的方差。
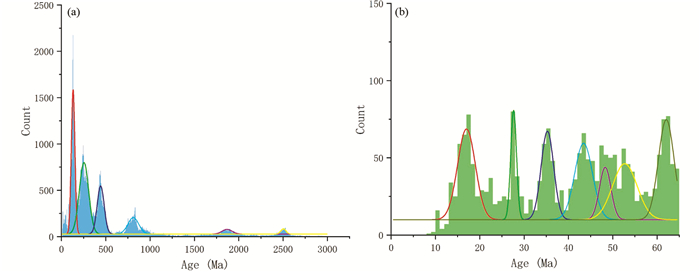
年龄-频数图中可拟合出多个(10)式所代表的年龄概率分布,每个概率分布的μ、σ不同。所得的6个年龄概率分布的μ对应的年龄分别为131.71Ma、255.17Ma、442.42Ma、811.56Ma、1868.36Ma和2505.31Ma。在5Ma的尺度上,由于新生代数据量少的原因,它并不能拟合具有确定性的年龄概率分布。因此以1Ma为区间长度,进行新生代的年龄-频数投图,发现其有明显的7个μ不同的年龄概率分布,其μ分别为:16.99Ma、27.64Ma、35.26Ma、43.44Ma、48.27Ma、52.74Ma和62.07Ma。年龄-频数图与拟合情况见图 4,拟合得出的概率分布的μ、σ等参数见表 4、表 5。
|
图 4 年龄-频数图与高斯多峰拟合结果 (a)所有年代;(b)新生代 Fig. 4 Age-frequency graph and Gaussian multi-peak fitting results |
|
|
表 4 5Ma区间长度高斯多峰拟合结果 Table 4 The results of Gaussian multi-peak fitting with the interval length of 5Ma |
|
|
表 5 1Ma为区间长度的新生代高斯多峰拟合结果 Table 5 The results of Cenozoic Gaussian multi-peak fitting with the interval length of 1Ma |
年龄-频数图上每一个锆石年龄的概率分布意味着一次锆石集中生长事件,每一个概率分布的μ代表的时间点,为锆石生长峰期。有意思的是,6个年龄概率分布的μ对应的年龄131.71Ma、255.17Ma、442.42Ma、811.56Ma、1868.36Ma和2505.31Ma分别对应中国大陆6次重大地质事件,分别是燕山运动、印支运动、加里东运动、晋宁运动、吕梁运动和五台运动(柴东浩,1985;范承钧,1983;郭福祥,1992;郝杰等,1992;劳秋元等,1983;乔秀夫和王雪英,1984;孙勇,1991;吴根耀,2002;武铁山和徐朝雷,1982;杨振升和俞保祥,1984;尹赞勋等,1965;赵宗溥,1963)。新生代的16.99Ma、27.64Ma、35.26Ma、43.44Ma、48.27Ma、52.74Ma和62.07Ma,也主要表现在喜马拉雅造山带,与两大陆碰撞、新生代气候时间也有耦合关系。限于数据库建设的阶段性和本文篇幅,数据得出的结果与地质历史事件的联系还需更进一步的探究。
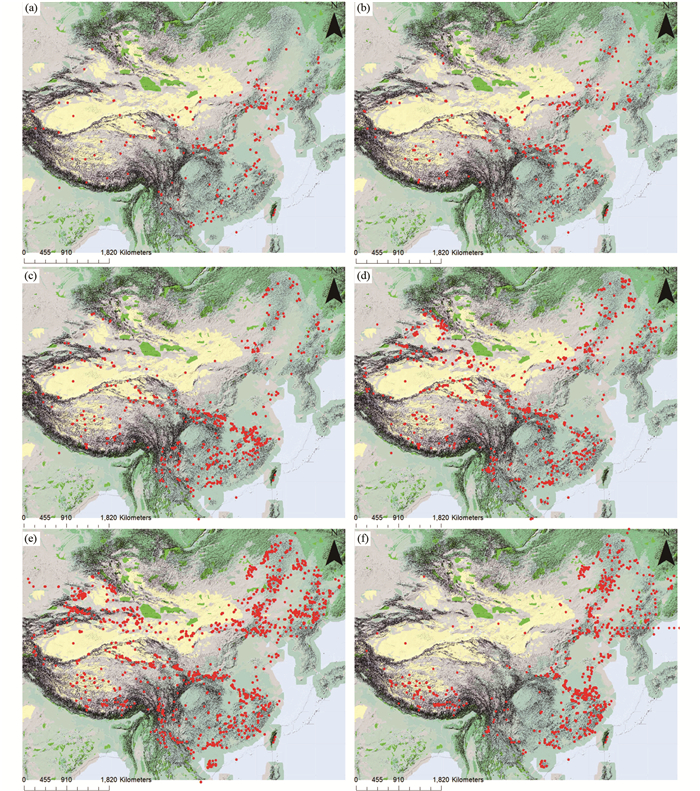
3.4 年龄概率分布在中国大陆的分区图在通过年龄-频数图可进行每个年龄概率分布的地区分布研究。通过高斯多峰拟合得到了各个年龄概率分布的μ与σ,利用2σ原则,将每个年龄概率分布的中间部分的95.44%的年龄所对应的样品测试点的位置投影在平面图中。投图的年龄区间为(μ-2σ, μ+2σ),见表 4、表 5,投图结果见图 5、图 6。
|
图 5 年龄概率分布对应测试点的位置 (a)μ=2505.31Ma的年龄概率分布;(b)μ=1868.36Ma的年龄概率分布;(c)μ=811.56Ma的年龄概率分布;(d)μ=442.42Ma的年龄概率分布;(e)μ=255.17Ma的年龄概率分布;(f)μ=131.71Ma的年龄概率分布 Fig. 5 Location of test points corresponding every probability distribution |

|
图 6 新生代年龄概率分布对应测试点的位置 (a)μ=62.07Ma的年龄概率分布;(b)μ=52.74Ma的年龄概率分布;(c)μ=48.27Ma的年龄概率分布;(d)μ=43.44Ma的年龄概率分布;(e)μ=35.26Ma的年龄概率分布;(f)μ=27.64Ma的年龄概率分布;(g)μ=16.99Ma的年龄概率分布 Fig. 6 Location of the corresponding test points of every Cenozoic probability distribution |
μ=2505.31Ma的年龄概率分布对应的测试点零星散布于青藏高原、华南、华北地区。μ=1868.36Ma、μ=811.56Ma、μ=442.42Ma与μ=255.17Ma的年龄概率分布对应的测试点基本遍布全国各地。μ=131.71Ma的年龄概率分布对应的测试点主要在青藏高原、中国东部,在西北部缺失。新生代的年龄概率分布对应的测试点主要位于喜马拉雅一带,相对来说东部只有零星分布。这些年龄概率分布对应测试点的位置与中国大陆的发展历程中的地质历史事件相关。
4 结论(1) 通过收集包括期刊论文与学位论文在内的中文文献中的单颗粒锆石U-Pb年代学数据,已建成中国大陆地壳单颗粒锆石U-Pb年代学数据库中文子库。中文子库包括文献库与数据库,其中数据库含154768条数据条目。每个数据条目含有样品测试号、样品岩性、样品采集位置等样品背景信息;测试方法、标样等技术背景信息;Pb、U、Th等的含量、Th/U、同位素比值及误差、年龄及误差等测试数据信息。
(2) 中文子库中年龄-年龄绝对误差关系的分析表明,Age(206Pb/238U)、Age(207Pb/235U)、Age(207Pb/206Pb)在不同的地质年代区间误差表现有所不同。对于所有方法来说,在小于1684.4Ma、1684.4~2855.2Ma、大于2855.2Ma年龄区间Age(206Pb/238U)、Age(207Pb/235U)、Age(207Pb/206Pb)的误差最小、置信度最好,可分别作为该年龄段的推荐年龄。LA-ICP-MS、SHRIMP、SIMS 3种方法选择出的推荐年龄具体的分界点与所有方法相比有较大区别,但总体的顺序都是一致的。LA-ICP-MS推荐年龄分界点为1835.3Ma、3078.1 Ma;SHRIMP为1382.7 Ma、1913.6 Ma;SIMS为887.6 Ma、1807.3 Ma。选用的推荐年龄运用于LA-ICP-MS、SHRIMP、SIMS三种方法的比较,12亿年以来LA-ICP-MS的年龄误差最小,元古代至约12亿年前SIMS年龄误差最小,太古代及以前SHRIMP年龄误差最小。有必要说明,因为Age(207Pb/235U)测试原理方面的原因,不宜作为年龄结果获取的最佳推荐年龄,应予综合考虑。
(3) 推荐年龄运用于年龄-频数图中,并使用高斯多峰拟合,则可发现中国大陆锆石存在μ分别为131.71Ma、255.17Ma、442.42Ma、811.56Ma、1868.36Ma和2505.31Ma等6个年龄概率分布,分别是燕山运动、印支运动、加里东运动、晋宁运动、吕梁运动和五台运动。更精细尺度下的新生代则存在μ分别为16.99Ma、27.64Ma、35.26Ma、43.44Ma、48.27Ma、52.74Ma和62.07Ma等7个年龄概率分布。年龄概率分布可与中国大陆地质历史事件对应。
致谢 感谢审稿人提出的修改意见。感谢北京大学地球与空间科学学院杨江南、卢亚敏、凌坤、胡圣懿、孔淑媛、熊轶伟、李华成、商修齐、冀锐、鲁学云,及学院2015级1班在数据库建设中的贡献。感谢SHRIMP实验室和北京大学LA-ICP-MS实验室以及马芳老师为本文作者提供的参观和指导。论文引用文献高达2331篇,参考文献拥有相关数据库可查询,不便一一列出,特此感谢数据源文献作者和数据测试实验室。
Bahlburg H and Berndt J. 2016. Provenance from zircon U-Pb age distributions in crustally contaminated granitoids. Sedimentary Geology, 336: 161-170. DOI:10.1016/j.sedgeo.2015.08.006 |
Chai DH. 1985. On the Zhongtiao Movement. Regional Geology of China, (15): 89-98. |
Condie KC, Belousova E, Griffin WL and Sircombe KN. 2009. Granitoid events in space and time:Constraints from igneous and detrital zircon age spectra. Gondwana Research, 15(3-4): 228-242. DOI:10.1016/j.gr.2008.06.001 |
Condie KC and Aster RC. 2010. Episodic zircon age spectra of orogenic granitoids:The supercontinent connection and continental growth. Precambrian Research, 180(3-4): 227-236. DOI:10.1016/j.precamres.2010.03.008 |
Condie KC, Arndt N, Davaille A and Puetz S. 2017. Zircon age peaks:Production or preservation of continental crust?. Geosphere, 13(2): 227-234. DOI:10.1130/GES01361.1 |
Fan CJ. 1983. Lancang movement:Structural movement of Indo-Sinian tectonic age in Sanjiang fold system. Contribution to the Geology of the Qinghai-Xizang (Tibet) Plateau, (4): 1-10. |
Guo FX. 1992. On the nature of the "Indo-Sinian Movement" of South China. Yunnan Geology, 11(2): 169-180. |
Guo H. 2011. A simple algorithm for fitting a Gaussian Function (DSP Tips and Tricks). IEEE Signal Processing Magazine, 28(5): 134-137. DOI:10.1109/MSP.2011.941846 |
Hao J, Li YJ and Hu WH. 1992. Problems related to the Jinning Movement and the Simian System. Regional Geology of China, (21): 131-140. |
Iizuka T, Hirata T, Komiya T, Rino S, Katayama I, Motoki A and Maruyama S. 2005. U-Pb and Lu-Hf isotope systematics of zircons from the Mississippi River sand:Implications for reworking and growth of continental crust. Geology, 33(6): 485-488. DOI:10.1130/G21427.1 |
Lao QY, Suo ST and Tan YJ. 1983. Proterozoic tectonics of China. Geological Review, 29(2): 111-120. |
Puetz SJ, Ganade CE, Zimmermann U and Borchardt G. 2018. Statistical analyses of Global U-Pb Database 2017. Geoscience Frontiers, 9(1): 121-145. |
Qiao XF and Wang XY. 1984. New stipulation concerning the Lvliang orogeny. Geological Review, 30(2): 177-178. |
Rino S, Komiya T, Windley BF, Katayama I, Motoki A and Hirata T. 2004. Major episodic increases of continental crustal growth determined from zircon ages of river sands:Implications for mantle overturns in the Early Precambrian. Physics of the Earth and Planetary Interiors, 146(1-2): 369-394. DOI:10.1016/j.pepi.2003.09.024 |
Song B. 2015. SHRIMP zircon U-Pb age measurement:Sample preparation, measurement, data processing and explanation. Geological Bulletin of China, 34(10): 1777-1788. |
Sun Y. 1991. The ancient ocean and Caledonian orogeny in the East Qinling. Geological Review, 37(6): 555-559. |
Williamson DF, Parker RA and Kendrick JS. 1989. The box plot:A simple visual method to interpret data. Annals of Internal Medicine, 110(11): 916-921. DOI:10.7326/0003-4819-110-11-916 |
Wu GY. 2002. The Yanshanian orogeny and Late Mesozoic activation in china continent. Chinese Journal of Geology, 37(4): 453-461. |
Wu TS and Xu CL. 1982. On the Lvliang Movement. Geological Review, 26(3): 240-244. |
Yang ZS and Yu BX. 1984. Palaeo-tectonics and its evolution of the Late Precambrian in East China. Journal of the Changchun College of Geology, (2): 1-20. |
Yin ZX, Xu DY and Pu QY. 1965. Compilation of the data of crustal movement name, China. Geological Review, 23(Suppl.): 20-81, 83. |
Zhao ZP. 1963. The Yanshanian in the east of China. Scientia Geologica Sinica, (3): 128-138. |
柴东浩. 1985. 关于中条运动. 中国区域地质, (15): 89-98. |
范承钧. 1983. 三江褶皱系的印支期构造运动——澜沧运动. 青藏高原地质文集, (4): 1-10. |
郭福祥. 1992. 华南"印支运动"的性质. 云南地质, 11(2): 169-180. |
郝杰, 李曰俊, 胡文虎. 1992. 晋宁运动和震旦系有关问题. 中国区域地质, (2): 131-140. |
劳秋元, 索书田, 谭应佳. 1983. 中国的元古宙构造. 地质论评, 29(2): 111-120. DOI:10.3321/j.issn:0371-5736.1983.02.002 |
乔秀夫, 王雪英. 1984. 吕梁运动新厘定. 地质论评, 30(2): 177-178. DOI:10.3321/j.issn:0371-5736.1984.02.010 |
宋彪. 2015. 用SHRIMP测定锆石U-Pb年龄的工作方法. 地质通报, 34(10): 1777-1788. DOI:10.3969/j.issn.1671-2552.2015.10.002 |
孙勇. 1991. 东秦岭古洋盆与加里东运动. 地质论评, 37(6): 555-559. DOI:10.3321/j.issn:0371-5736.1991.06.008 |
吴根耀. 2002. 燕山运动和中国大陆晚中生代的活化. 地质科学, 37(4): 453-461. DOI:10.3321/j.issn:0563-5020.2002.04.009 |
武铁山, 徐朝雷. 1982. 吕梁运动讨论. 地质论评, 26(3): 240-244. DOI:10.3321/j.issn:0371-5736.1982.03.007 |
杨振升, 俞保祥. 1984. 中国东部晚前寒武纪古构造及其演化. 长春地质学院学报, (2): 1-20. |
尹赞勋, 徐道一, 浦庆余. 1965. 中国地壳运动名称资料汇编. 地质论评, 23(增): 20-81, 83. |
赵宗溥. 1963. 中国东部的燕山运动. 地质科学, (3): 128-138. |
 2018, Vol. 34
2018, Vol. 34


