成矿预测是实现科学找矿、扩大资源储量的重要途径和方法(赵鹏大，2007)。自20世纪40~50年代起，其相关研究经历了从定性到定量、再到定位定量预测的发展阶段(袁峰等，2014)。1975年，国际地质科学联合会在国际上推出了第一代标准矿产资源定量评价方法，包括区域价值估计法、体积估计法、丰度估计法、矿床模型法、德尔菲法和综合法等六种。这些方法主要运用地质、地球化学、地球物理、数学和经验知识，将专家观点(经验知识)、地质条件、矿床类型等因素通过一定的规则集(推理网络)综合考虑，进行找矿预测(Harris, 1978)。其中，影响结果的最大因素是从业者的经验知识。通过前期矿产勘查预测的实践积累，逐渐形成“在勘查程度较高的地区建立起单/多变量的频率分布模型，用来预测未勘查或勘查程度较低的地区”的找矿模式(Singer and Mosier, 1981)。通过对地质变量的多元回归分析，对未知区地质特征进行分类，进而建立起各种地质空间模型。这种地质空间模型的外延和变异均可用于成矿预测(Trapp and Rockaway, 1977)。但是，矿产勘查与预测要考虑的变量实在太多了，人们通常并不能很好地把握这些变量。因此，人们经常通过一些方法使得原始变量被分解为数量更少的新变量，达到降维目的，从而提取特征因素并使结果更容易被理解。

20世纪90年代，美国提出矿产资源“三步”定量评价(Singer, 1993)，按照“目标矿床类型的有利地段→合适的标准品味吨位模型→可能存在的矿床数量”这一思路进行找矿预测。但实际上，同一地质条件下可能会有多种成矿类型，使得预测变得复杂困难。应用“数理统计、模糊数学和经验方法”从地质背景中圈出“地质异常”，并以成矿多样性分析与矿床谱系研究为指导，将地质异常、成矿多样性及矿床谱系三方面定量化研究紧密结合形成“三联式”资源定量预测与评价(赵鹏大和胡旺亮，1992；赵鹏大，2002)。在一定的地质构造单元和地质发展阶段内，一定的成矿作用会在不同的成矿阶段和地质构造部位形成不同的矿种，即成矿系列(陈毓川，1994)。利用成矿系列缺位，即通过确定在某些地段应当存在但尚未发现的某类矿床进行成矿预测(王登红等，2006)。伴随着GIS技术的发展和应用，业内逐渐形成以找矿模型为基础，将地质体和矿体视作单元，利用GIS技术研究地质体对矿体的控制作用并进行成矿预测(王世称，2010)。将多重分形原理与成矿过程、矿产资源分布规律、矿产资源信息获取研究相结合，以“奇异性-广义自相似性-分形谱系”为核心进行非线性成矿预测(成秋明, 2006)。周永章等(2017)分析了矿床大数据及智能矿床模型研究的背景与进展，建立了大数据智能矿产资源预测与找矿理论的基础。

在今天大数据时代，智能数据处理方法具有特别重要的价值。但大数据人工智能地质学刚刚起步，尚未成熟。因此，基于大数据智能算法及其应用的地质研究是非常有意义的探索性实验(张旗和周永章，2017；周永章等, 2017, 2018a)。大数据是人类对事物的海量已知描述，可以通过机器学习和深度学习来预测未来。成矿预测是人工智能地质学的重要任务之一。利用大数据和机器学习解决矿产预测问题，有助于人们克服不能全面考虑地质变量的困难及评估当前模型在已有数据中的可靠性。

本研究以安徽省兆吉口铅锌矿床为例，运用卷积神经网络分析方法，通过训练学习获得Pb元素地表分布与矿体赋存空间之间的逻辑回归关系，并利用训练所得模型进行矿产资源预测。

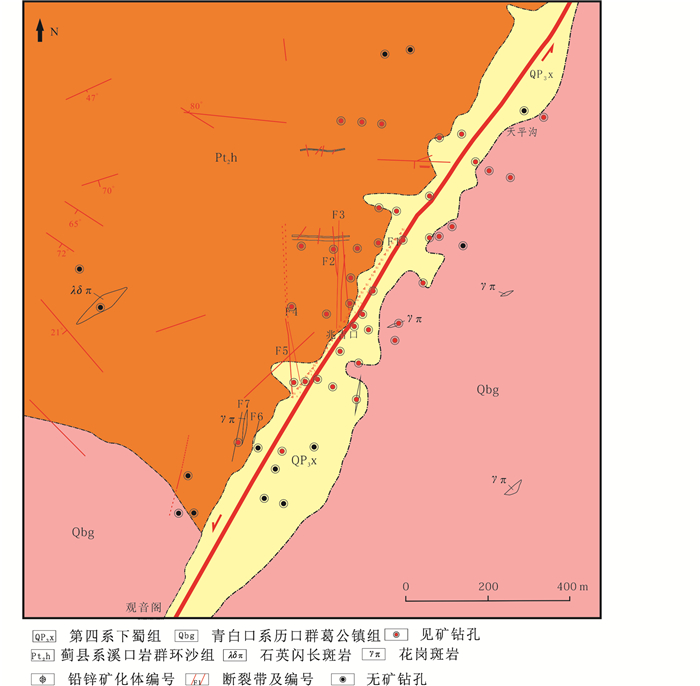
1 地质背景

兆吉口铅锌矿床位于东至县城SW200°方向18km处的杨老尖-龙门尖地区，大地构造位置处于扬子板块下扬子台拗和江南台隆的过渡部位、下扬子台坳石台穹褶断束南西部。区内主要构造方向为NNE向，各时代地层均发生了不同程度的褶皱，其中以印支期最为强烈。兆吉村倒转背斜、雷公尖向斜、官港倒转背斜属障公山复背斜西部的次级褶皱构造。区内断裂构造十分发育，规模较大的断裂构造有东至断裂、龙门尖断裂和许村断裂。矿床主要产于东至断裂的次级构造中，此外，东至断裂中也有产出，但矿体数量少，平均品位低(曹达旺等，2010)。矿体呈脉状、透镜状赋存于东至断裂及其南北向的张性次级裂隙破碎带中(图 1)。矿体与两盘的界线清晰，围岩蚀变不发育，据此认为其成矿方式为充填作用。上盘主要为新元古代青白口系历口群葛公镇组(Qbg)地层，下盘主要为中元古代蓟县系溪口群环沙组(Pt₂h)地层，地表为新生代第四系下蜀组(Qpx)覆盖。矿区地层岩性主要为变粉砂岩、变细砂岩和变粉砂质泥岩，具低绿片岩相浅变质特征。破碎带主要有碎裂岩(断层泥)、硅化构造角砾岩、硅化碎裂岩等构造岩(刘艳鹏等，2015)。矿区正北方向出露面积约1.5km²花岗闪长斑岩，呈近东西向长条状展布。岩脉出露较多，主要以石英闪长玢岩、花岗斑岩、石英闪长斑岩、闪长玢岩、辉绿玢岩和闪斜煌斑岩等中酸性岩脉为主。脉体围岩蚀变主要为高岭土化、绿泥石化、绢云母化，其中辉绿玢岩脉见明显的黄铁矿化蚀变(Liu et al., 2016)。

2 研究方法

人工神经网络是一种模仿生物神经网络行为特征，进行分布式并行信息处理的算法数学模型(van Gerven and Bohte, 2017)。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。本研究将元素在地表的含量以图像形式表示，然后采用卷积神经网络进行训练学习，依据所得模型进行找矿预测。

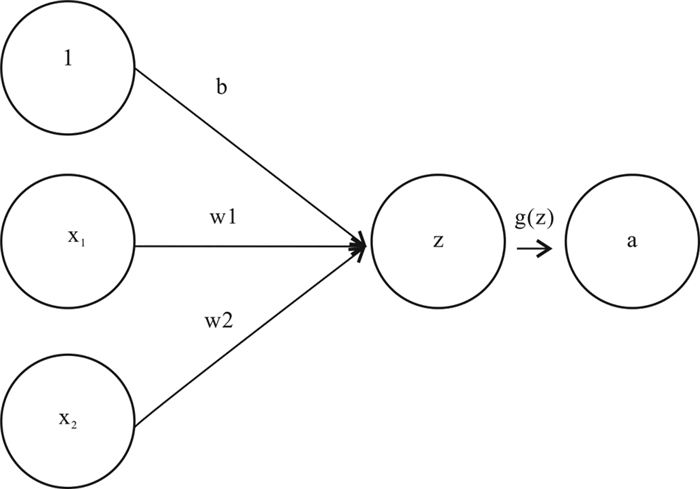
2.1 神经网络简介 2.1.1 神经元

神经元是神经网络的基础单元，一般称作为节点(node)，其结构如图 2。基本形式为wx+b，其中x₁、x₂表示输入向量，w₁、w₂为权重，b为偏置bias，g(z)为激活函数，a为输出。大量神经元相互连接组成神经网络。每个神经元接受一个或多个信号输入，经过激活函数变换后输出。神经元之间用权重(weight)连接。不同的权重和激活函数会导致神经网络不同的输出。

2.1.2 激活函数

激活函数定义了节点的输出结果。常用激活函数有Sigmoid、Tanh、ReLu等(Nair and Hinton, 2010)，前两者常见于全连接层，后者ReLu常见于卷积层(Lawrence et al., 1997)。Sigmoid函数如下式(1)所示:

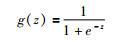
(1)

其中z是一个线性组合，比如z可以为：b+w₁×x₁+w₂×x₂。通过代入正无穷或负无穷到g(z)函数中可知，其结果趋近于0或1。即Sigmoid函数的功能是把一个实数压缩至0到1之间。把g(z)看作为分类的“概率”，比如激活函数的输出为0.9的话则解释为90%的概率为正样本。

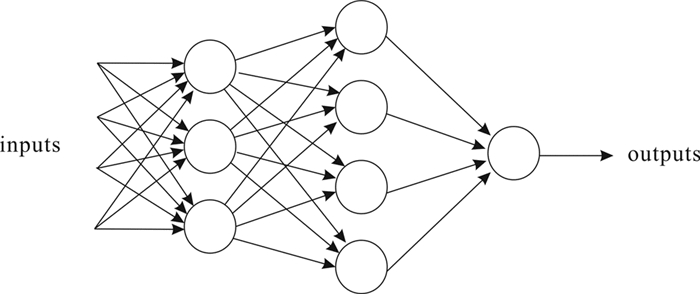
2.1.3 神经网络

神经网络由多个神经元按分层结构组织形成。通常通过没有特定于任务的编程考虑实例进行“学习”，逐步提高性能(Lawrence et al., 1997)。图 3是一个三层神经网络结构。图 3中最左边的原始输入信息称之为输入层(Input layer)，最右边的神经元称之为输出层(Output layer)，中间的为隐藏层(Hidden layer)。输入层是众多神经元接受大量非线性输入信息。输入的信息称为输入向量。输出层是新息在神经元链接中传输、分析、权衡，形成输出结果。输出的信息称为输出向量。隐藏层是输入层和输出层之间众多神经元和链接组成的各个层面。如果有多个隐藏层，则意味着多个激活函数。同时，每层由单个或多个神经元组成，当前层的输出作为下一层的输入数据，最终由输出层输出最终结果。输入层和输出层中间可以夹着数层隐藏层。层和层之间是全连接的结构，同层神经元之间没有连接。此外，输入层和隐藏层都存在一个偏置(bias unit)。

2.2 卷积神经网络

卷积神经网络(Convolutional Neural Network，CNN)是机器学习中的一种深度前馈人工神经网络分类方法，已经成功地应用于图像识别(Lawrence et al., 1997; Krizhevsky et al., 2012)。其使用需要最少预处理的多层感知器变量。多层感知器(Multi-layer Perceptron, MLP)是由输入层、隐含层(一层或者多层)及输出层构成的神经网络模型，可以解决单层感知器不能解决的线性不可分问题(Sainath et al., 2013)。基于它们的共享权重结构和平移不变性特征，也被称为移位不变或空间不变式人工神经网络(SIANN)。CNN结构通常包括输入层、卷积层、池化层、全连接层和输出层。其中，卷积层、池化层和全连接层构成多层感知器的隐藏层。

2.2.1 卷积层

卷积层(Convolutional layer)是CNN的基础，由若干特征面(Feature Map)组成，直接对原始输入信号进行卷积操作(Gao et al., 2016)。每层卷积层由若干卷积单元组成，每个卷积单元的参数都是通过反向传播算法最佳化得到的。卷积层通过局部连接和权值共享的方法，模拟具有局部感受野的简单细胞，提取一些初级视觉特征的过程。卷积运算的目的是提取输入的不同特征，第一层卷积层提取一些低级的特征如边缘、线条和角等层级，更多层的网路能从低级特征中迭代提取更复杂的特征。局部连接指卷积层上的每个神经元与前一层特征图中固定区域的神经元建立连接；权值共享指同一特征图中的神经元用一组相同的连接强度与前一层局部连接，可以减少网络训练参数。上述一组相同的连接强度即为一个特征提取器，在运算过程中表现为一个卷积核(Kernel)，卷积核是一个大小自定的权值矩阵(LeCun et al., 1998)。卷积核以一定步长在特征图上进行“滑动”，每滑动一次就进行一次卷积操作。通过多次的卷积操作提取输入信号的不同特征，每一个卷积核提取一种特征，这样n个卷积核就可以提取n种特征。通常卷积层的计算形式如下式(2)所示：

(2)

其中f()代表激活函数，K代表卷积核，l代表卷积层数，MJ是输入层的感受野，b代表每个输入图的一个偏置值。

2.2.2 池化层

池化层(Pooling Layer)是模拟复杂细胞将初级的视觉特征筛选并结合成更高级、抽象的视觉特征的过程，在网络中通过采样实现。经过池化层的采样后，输出特征图的数量不变，但是特征图的尺寸会变小，有减少计算复杂度、抵抗微小位移变化的作用。

2.2.3 全连接层

网络经过若干个特征提取层后会接入一个全连接层(Fully Connected Layer)。该层的每一个神经元与前一层的所有神经元互相连接，同层神经元之间不连接。该层有助于增强网络的非线性映射能力并且限制网络规模的大小。

2.3 数据处理

本研究主要利用研究区化探分析获得的Pb元素含量(刘艳鹏，2017)。经检验分析，Pb分析值均大于检出限，分析结果可靠有效。

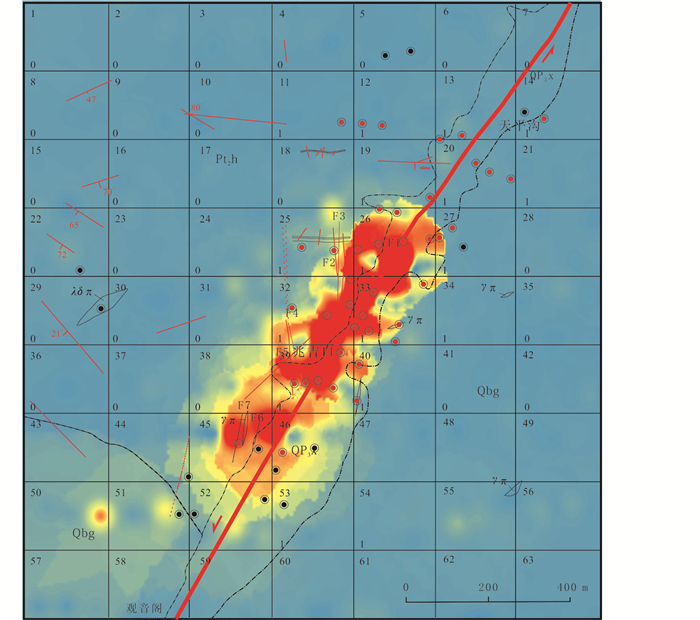
对研究区进行网格化，将研究区自西向东自北向南分成63个200×167m²的小格，编号为1~63。然后用克里格法插值，制成Pb浓度分布图，结果如图 4所示。

取1~42号作为训练样本。样品分为ore和non两类。参考逻辑回归分类原则为：如果小格内含有见矿孔，则标1表示有矿。如果小格内没有钻孔或钻孔未见矿，则标0表示无矿。由于21、34号紧邻见矿孔，故标为有矿。

取43~63作为预测样本。选择训练集30%的数据作为验证集。

本研究使用的卷积神经网络结构为：(卷积层+池化层)×2+(全连接层)×2+Softmax层。Loss函数为交叉熵(Cross Entropy)。Softmax层输出样本属于各类的概率。

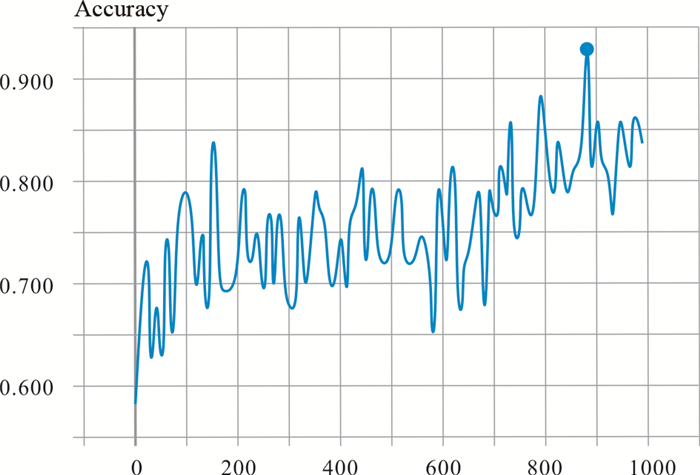
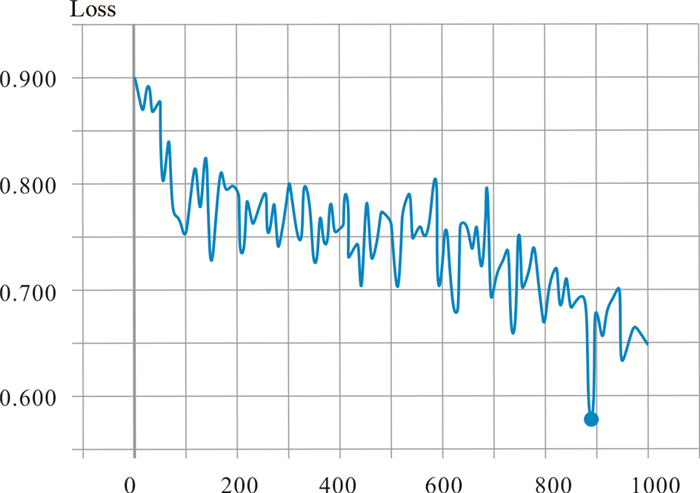
3 结果

本研究训练次数设定为1000次，训练集得到accuracy和loss分别如图 5、图 6所示。在第880步时，accuracy达到0.93，loss为0.28。此时验证集的accuracy为0.83，loss为0.38。表明训练模型相对已有数据来说是可靠的。利用所得模型对预测集进行预测，结果如表 1所示。45、46及53号区域为含矿区域。

4 讨论

以往地球化学勘查遵循“背景与异常分离”原则，通过统计学方法将元素含量人为分成背景和异常两大类。然而，背景和异常是一个“相对”的概念。在不同尺度下，背景和异常可以相互转换。比如，区域的异常可能落在矿区的背景里面，成为一种悖论。

本研究抛去传统的“背景与异常”思路，直接通过元素空间分布图像与矿体的相关性进行找矿预测。其训练集和验证集准确率分别达到0.93和0.83，表明该模型可靠。

45、46及53号区域预测结果为含矿。其中，45、46号区域的含矿预测概率均为1，已有钻孔工程确实在该区打着矿体，进一步证实了该模型的可靠性。53号区域的含矿概率为0.82，表明该区含矿的可能性非常大，但已有钻孔并未打着矿体，说明这些钻孔设计的位置或深度不合适。

通过元素空间分布图像与矿体的相关性进行找矿预测的原理可能是元素在地表的次生分布特征受成矿作用的影响，地表分布中具有表达矿体就位地表响应的特征量，可以称之为成矿特征量。兆吉口元素地表分布影响因素主要有原岩成分、成矿作用影响和地表风化(刘艳鹏，2017；刘艳鹏等，2017)。原岩成分决定了元素在地表的基本分布特征，成矿作用将矿床形成过程中的元素迁移变化特征叠加到原岩的原岩含量特征上。这种迁移变化特征中携带某些指示矿体就位的信息，即矿体在地下空间就位时在地表的响应，且未在风化过程中消失。以往的地球化学勘查工作仅仅识别异常，但未能发现矿体在地表响应的成矿特征量。本文通过机器学习，利用卷积神经网络，不断挖掘元素分布特征与矿体地下就位空间的耦合相关性，最终建立起accuracy=0.93，loss=0.28的卷积神经网络模型。这种神经网络模型表达的可能就是矿体在地下就位时元素在地表分布的响应。

5 结论

本文利用大数据机器学习的思维，运用卷积神经网络学习安徽省兆吉口铅锌矿床地表Pb分布特征与矿体就位空间关系，然后进行成矿预测，得到以下结论：

卷积神经网络可以有效挖掘地表元素分布与矿体就位空间关系。通过训练，建立起accuracy=0.93，loss=0.28的卷积神经网络模型。这种模型在已有的数据中是有效的。

53号区域大概率存在未发现的矿体。预测集中45、46及53号区域预测结果为含矿，其中，45和56号区域已被证实，53号区域中的已有钻孔位置或深度不合适。建议重新在53号区域有利地点布孔验证。