玄武岩是一种喷出岩，其化学成分与辉长岩或辉绿岩相似，SiO₂含量介于45%~52%之间，CaO、Fe₂O₃+FeO、MgO含量较侵入岩略低。作为一种大洋和大陆广泛分布的基性火山岩，玄武岩成因理论主要是在对大火成岩省研究的基础上奠定的，例如玄武岩的形成、演化、分异、分离结晶的理论等。根据大地构造环境理论，通常将玄武岩按产出的构造环境不同划分为以下三类：发育于深海洋脊的玄武岩、发育于洋盆内群岛和海山的玄武岩、发育于岛弧和活动大陆边缘的玄武岩。其中，大洋中脊玄武岩(MORB)、洋岛玄武岩(OIB)和岛弧玄武岩(IAB)是学术界最关心的三种玄武岩类型。MORB是在大洋中脊喷出，位于海平面以下，探测难度较大；OIB特指不和任何俯冲有关的玄武岩，一般规模较小，如夏威夷、斐济等；而IAB多数出露在海平面以上，绵延几百乃至上千千米，规模大小不一(汪云亮等, 2001)。

玄武岩大地构造环境理论主要是以板块构造理论为基础创立的。板块构造理论于二十世纪五、六十年代创立，其创建推进了玄武岩地球动力学研究的飞速发展，尤其是玄武岩构造环境判别方法的引入，大大提高了玄武岩在地球动力学、大地构造背景研究中的作用和地位。根据岩浆岩的地球化学特征判别岩浆形成的大地构造环境和岩浆源区的化学性质，在二十世纪七、八十年代发展较快，并提出了一系列以图解为基础的判别理论和应用方法(Floyd and Winchester, 1975; Whalen et al., 1987)。这些方法集中在对地壳中分布较为广泛的玄武岩、花岗岩等岩浆岩的判别，玄武岩判别图解法由此渐趋成熟。值得一提的是，以Pearce and Cann(1971, 1973)为首的学者最早提出了玄武岩构造环境判别图，将构造环境与玄武岩地球化学特征有机结合起来，为板块构造和大陆造山带研究开辟了新的途径。玄武岩判别图也因其扎实的理论基础和简明的表达方式，得到了学术界的广泛应用，极大地丰富了玄武岩研究的内容，同时将玄武岩构造环境研究推向高峰。

随着地球化学研究的深入，众多学者认识到岩浆地幔源区具有高度的不均一性、地幔复杂的交代机制以及岩浆作用过程是对岩浆成因及其形成的构造背景的重要制约因素，并发现早先构建的玄武岩构造环境判别图存在许多问题(张旗, 1990; Li et al., 2015; 罗建民等, 2018)：(1)理论基础少，多以经验为主，主观性较强；(2)判别图种类繁多，而每种图的适用范围有其局限性；(3)对于同一样品，不同判别图可能给出相互矛盾的结果；(4)将构造环境判别简单化，不利于岩浆作用过程及其动力学的深入研究；(5)有些判别图的制作仅用局部地区部分样本，若增大样本量，则图中的分类界线将失去分类作用；(6)所使用的元素数据仅为2~3个，信息量有限，导致分类结果比较片面。因此，国内外学者不仅减少了对玄武岩判别图的使用，而且提出了诸多质疑和批判。近年来，随着大数据、云计算等新技术的快速发展以及计算机硬件运算能力的大幅提高，数据挖掘算法逐渐受到国内外学者的密切关注，并在模式识别、函数逼近、建模仿真等方面获得了丰硕成果。然而，在玄武岩地球化学这一领域，目前国内外对于应用数据挖掘算法判别玄武岩构造环境的研究尚处于起步阶段(Petrelli and Perugini, 2016; 王金荣等, 2017; Karpatne et al., 2018; 周永章等, 2018)。本文针对传统判别图的固有问题，采用大数据智能挖掘算法建立判别模型，通过输入玄武岩化学成分来对其构造环境进行判别，以此提高构造环境判别过程的效率和准确性。此外，通过对判别图解法和智能算法判别正确率进行对比，结果表明智能算法判别玄武岩构造环境比判别图解法更为准确、迅速，可以考虑在该领域作进一步推广应用。

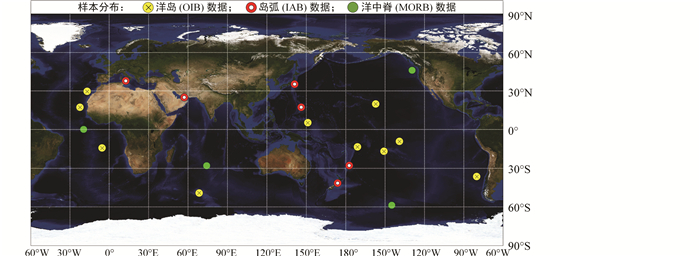
1 判别图分析 1.1 判别图概述

Pearce and Cann (1973)最先提出根据化学成分来限定岩浆起源的大地构造背景，随后迅速涌现大量研究支持这一认识，判别图因此得到了广泛应用。判别图主要分为主量元素判别图和微量元素判别图两大类，其判别原理如下：确保研究样品满足一定要求后，应用统计学规律将研究样品划归成不同的类型，并根据不同类型样品的元素浓度进行投图，以此显现不同类型样品间的分界线。王金荣等(2016)、杨婧等(2016a, b)、陈万峰等(2017)、第鹏飞等(2017)等利用大数据方法对判别图的使用作了较为深入的研究，并提出了许多值得重视的见解，指出需要查明不同判别图的应用范围和条件，才能获得比较满意的判别结果，而如果使用不当则会造成错判。因此，本次研究选取240个MORB(如东太平洋海隆、大西洋中洋脊、印度洋等)、259个OIB(如圣赫勒拿岛、加那利群岛、社会群岛等)以及256个IAB(如伊豆群岛、千岛群岛、汤加弧、马里亚纳群岛等)作为研究样品，所用样品全球分布如图 1所示，利用几个典型的玄武岩判别图对上述样品进行大地构造环境判别尝试。

1.2 判别图解 1.2.1 微量元素图解

(1) Ti-Zr-Y图

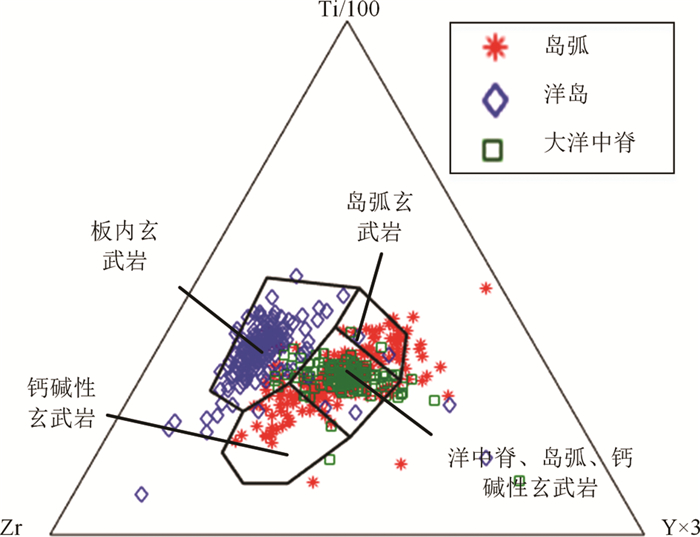
Ti-Zr-Y图是Pearce and Cann (1971)首次提出来的，共使用200多个样品，包括岛弧拉斑玄武岩46个，岛弧钙碱性玄武岩60个，岛弧橄榄安粗岩6个，洋底玄武岩82个。Pearce et al. (1984)认为，该图最大的优点是能够把OIB与MORB和IAB区分开，还强调该图区分上述玄武岩的有效率高达95%以上，从而认为该图是最为有效的鉴别板内玄武岩与非板内玄武岩的判别图。

考虑到部分样品中Ti、Y、Zr某一微量元素为空值，不满足Ti-Zr-Y判别图绘制条件，故须提前剔除空值对应样品，从而得到MORB、OIB、IAB的有效样品量，见表 1。通过对有效样品进行投图(如图 2所示)可以发现，IAB的分布较为分散，区分度较低。三类玄武岩在一定区域的重叠度较高，因此很难正确判别出其种类。由表 1定量结果可知，未剔除无效样品判别正确率不超过60%，剔除无效样品后判别正确率能达到85%以上。

(2) Ti-Zr图

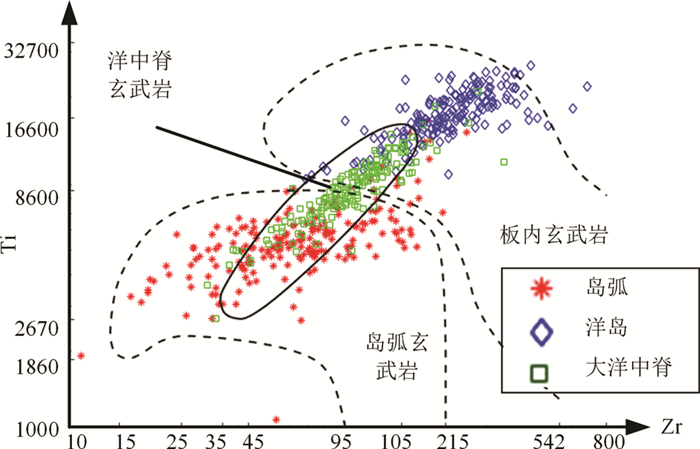
Ti-Zr图最初是由Pearce and Cann (1973)提出来的，此后Pearce (1982)又对其作了修正，该图最大的优势是对板内玄武岩和岛弧玄武岩的区分度较好。由图 3(577个有效样品投图形成)可见，OIB和IAB界限较为分明，而MORB由于呈线性关系展布，重叠区域较大，因而无法有效辨别MORB。从表 2来看，在不考虑无效样品的情况下，该图判别准确率可达90%以上，若顾及已剔除样品，该图对三类岩石的判别准确率不足75%。

(3) Zr/Y-Zr图

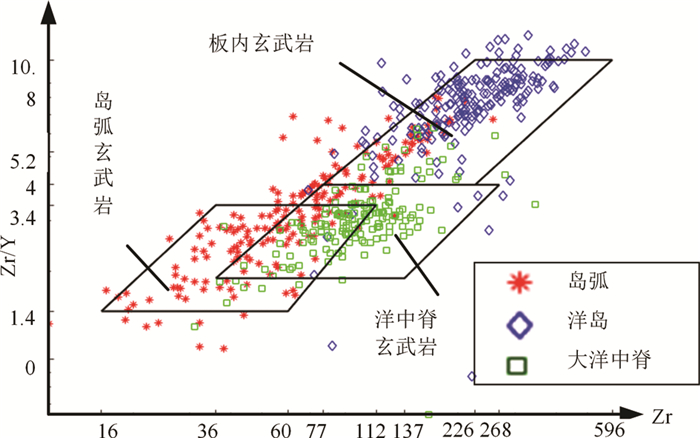
Zr/Y-Zr图由Pearce and Norry (1979)提出用来辨别岛弧(或火山弧)玄武岩、洋中脊玄武岩和板内玄武岩的。Pearce and Norry (1979)将Zr/Y=3作为区分板内玄武岩与非板内玄武岩的分界线，但是对有效样品(576个)进行投图(如图 4所示)后，发现IAB分布范围较广，且有部分IAB、MORB进入板内玄武岩区域，致使该区域区分度较低，说明Zr/Y=3作为区分界线有待考证。表 3中，考虑所有样品总体正确率不到60%，筛选掉无效样品后，判别正确率能提高到80%左右，也证实了上述观点。

1.2.2 主量元素图解

(1) FeO^T-MgO-Al₂O₃图

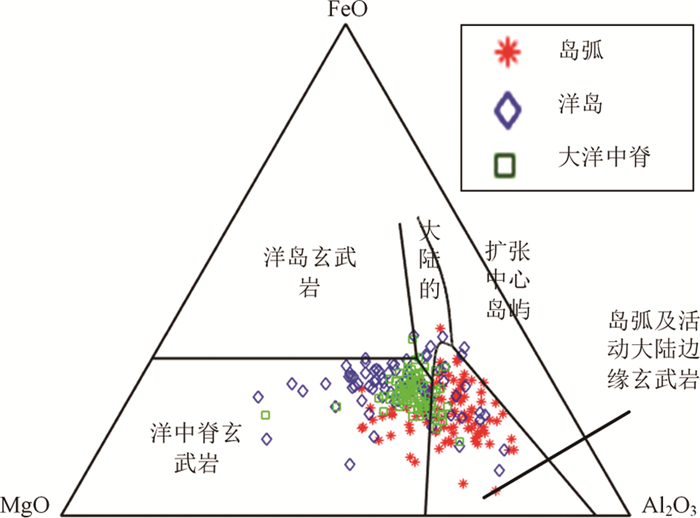
FeO^T-MgO-Al₂O₃图是Pearce et al. (1977)利用了8400个数据(包括652个洋底和洋脊的数据)设计的，适用于SiO₂含量为51%~56%的玄武岩。由于设计资料较为丰富，该图可判别5类玄武岩构造环境，分别为洋岛玄武岩、洋中脊玄武岩、岛弧及活动大陆边缘玄武岩、扩张中心岛屿以及大陆玄武岩。观察图 5各区域，同时结合表 4记录的样品量可知，由于筛选掉的样品数量(455个)过大，导致对OIB的投图效果较差，B、C两区域的区分率也较低。表 4中判别正确率过低进一步验证了FeO^T-MgO-Al₂O₃图不能有效鉴别MORB、OIB和IAB。

(2) TiO₂-MnO-P₂O₅图

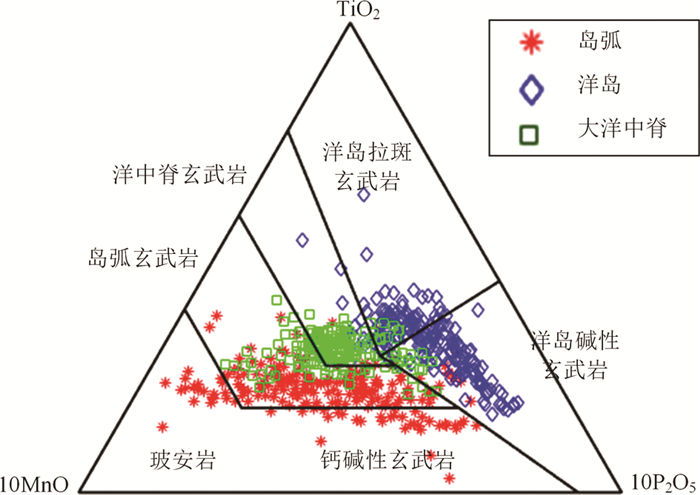
TiO₂-MnO-P₂O₅图是由Mullen (1983)设计的，用来判别SiO₂含量为45%~54%的5类玄武岩大地构造背景：玻安岩(Bon)、钙碱性玄武岩(CAB)、岛弧拉斑玄武岩(IAT)、洋中脊玄武岩(MORB)、洋岛拉斑玄武岩(OIT)和洋岛碱性玄武岩(OIA)，共使用507个样品，其中MORB样品130个。从图 6来看，OIB的投图效果最好，而MORB和IAB都超过了划定范围。由表 5可得，玄武岩判别准确率整体上较前几个判别图略好，但考虑到已剔除样本，总体判别正确率仍不足72%。

2 机器学习判别 2.1 算法原理简述

数据挖掘算法对已知样品数据进行训练，自主构建分类模型，避免人为因素干扰，能够更加科学客观地判别玄武岩构造环境。研究样品中包含大量不完整的、含有噪声的无效数据，难以用一般数理统计方法进行分类处理，而采用数据挖掘技术能够从大量信息中提取出潜在数据模式或知识规律(周志华, 2016)，有助于准确判别三类玄武岩。根据所选数据的特点，拟用朴素贝叶斯(Naive Bayes, NB)、K近邻(K-Nearest Neighbors, KNN)、支持向量机(Support Vector Machine, SVM)以及随机森林(Random Forest, RF)四种分类算法来辅助分析样品特征属性并建立分类模型。现将上述四种算法的利弊总结如下(周志华, 2016)：(1)NB算法有严谨的数学理论支持，且有稳定的分类效率，对缺失数据不敏感，但是当不同属性之间存在相关性时，会严重影响分类效率；(2)KNN算法分类准确度高，对异常值不敏感、无数据输入假定，但是其计算复杂度和空间复杂度较高，致使计算开销过大；(3)SVM算法泛化错误率低，分类速度快，结果易解释，但其对缺失数据较为敏感，且受核函数和参数选取的影响较大；(4)RF算法适合处理高维数据，能够检测到属性间的互相影响，并在部分特征遗失的情况下仍可维持较高的分类准确度，但其在解决某些噪音较大的问题时易过拟合。

(1) 朴素贝叶斯(NB)(Kononenko, 1993; Domingos and Pazzani, 1997)

NB算法是基于贝叶斯定理的概率统计学分类方法。设每个数据样本用一个n维特征向量来描述n个属性的值，即X={x₁, x₂, …, x_n}，假定有m个类，分别用C₁, C₂, …, C_m表示。给定一个未知的数据样本X，若NB算法将该样本X分配给类C_i，则一定存在以下关系：

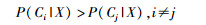
(1)

依据贝叶斯定理，由于P(X)对于所有类均为常量，最大化后验概率P(C_i|X)可转化为最大化先验概率P(X|C_i)P(C_i)。如果训练数据集包含较多特征属性，导致P(X|C_i)计算开销较大，为此，通常假设各属性之间互相独立，于是，对于给定的待分类样本X，可以先利用贝叶斯公式分别计算出X属于每一个类别C_i的概率P(X|C_i)P(C_i)，然后选择其中概率最大的类别作为其类别。

(2) K近邻(KNN)(Cover, 1967; Altman, 1992)

KNN算法是最简单的机器学习分类算法之一。如果将每一训练样本作为n维空间中一点，那么所有训练样本均可存放于n维空间中。当给定一未知类别的样本时，通过搜索该n维特征空间并找出最接近该未知样本的k个样本。若该样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。两样本X={x₁, x₂, …, x_n}和Y={y₁, y₂, …, y_n}间的邻近性常用欧式距离来描述：

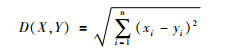
(2)

(3) 支持向量机(SVM)(Cortes and Vapnik, 1995; Li et al., 2014)

基于统计学VC维理论和最小结构风险原理的SVM算法广泛应用于处理二元分类问题。SVM算法的基本思想是通过训练样本找出一个最优分离超平面，使得两类样本能够正确分离，并且误差概率最小和分隔间距最大。若将SVM分类问题看成一个函数f(x)，那么最优化问题就是求该函数最小值。对于线性问题，将寻求最优分类平面转化为求解二次规划问题，采用拉格朗日乘子法即可解决约束优化问题：

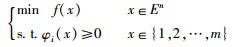
(3)

对于非线性问题，引入适当的核函数k(x_i, x)后，可将输入变量转换为某个高维空间实现线性可分离，来求取最佳分类平面，该分类器为：

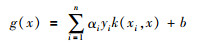
(4)

式中：g(x)为分类器；α_i为拉格朗日因子；(x_i, y_i)为已知样本；x为未知数；k(x, x_i)为核函数。

(4) 随机森林(RF)(Breiman, 2001)

RF算法是由多个决策树模型{h(X, L_k)|k=1, 2, …}组成的集成学习方法。已知{L_k}是独立同分布的随机向量，用来控制树的生长。RF通过自助法重采样技术，从训练样本集中有放回地重复随机抽取k个样本生成新的训练样本集，然后根据自助样本集生成k个分类树组成随机森林，得到新的序列{h₁(X, L₁), h₂(X, L₂), …, h_k(X, L_k)}。在给定的自变量X下，每个决策树会给出一结果，最终分类结果取决于各个决策树结果的简单多数投票，其公式如下：

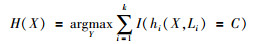
(5)

式中：H(X)为随机森林模型；C为样本标签；I为示性函数。

2.2 算法判别实验

(1) 确定研究样品

与判别图解相同，机器学习判别仍选用755个玄武岩样品(240个MORB、259个OIB以及256个IAB)作为研究对象，所用样品全球分布同见图 1。现将每个样品看成是一个51维行向量，包含11维主量元素、35维微量元素和5维同位素，详见表 6。不同于判别图解实验的是在利用智能算法判别玄武岩构造环境时，所有数据(包括空值数据)均视为有效数据，不作任何数据剔除，以确保全部样品进行判别实验。

(2) 算法参数寻优

算法分类模型是在通过反复迭代改变参数，对训练样本不断实验的基础上完善其工作性能的(Bishop, 2006)。采用智能算法进行玄武岩种类判别，为达到最佳分类效果，需采用K-重交叉验证法调整各个分类模型的关键参数，以此提高算法的分类准确度。例如，NB算法是否设置先验概率，KNN算法中最近邻样本数量k的取值，SVM算法核函数的选取，RF算法中决策树数目以及每棵树最大深度的拟定。经多次验证与比较，现将各个算法最佳执行参数及其使用注意事项记录于表 7中。

(3) 算法判别结果

一方面，为了定量评价上述四种智能算法的分类性能，另一方面，考虑到要与判别图解所得结果进行对比，通过计算得到各个算法的样品正确分类数目、构造环境判别正确率以及总体判别正确率，计算结果见表 8。表中结果显示，在全部样品数据用于模型训练的情况下，NB的分类结果最差，仅有75.67%，而RF分类准确率竟高达100%。

2.3 结果对比——判别图法与智能算法

现将考虑所有样品下的判别图解分类正确率汇总于表 9中，与表 8结果进行比较可以发现，尽管NB在四种智能算法中分类正确率最差，但仍优于判别图解法中判别效果较好的微量元素Ti-Zr判别图和主量元素TiO₂-MnO-P₂O₅判别图。此外，从表 1-表 5、表 9整体来看，判别图存在以下问题：其一，是否考虑剔除数据对判别正确率的影响较大；其二，三种构造环境的判别正确率相差较大。而SVM、RF的判别正确率分别能达到98%、100%，且三种构造环境的判别效果较为接近，从而表明智能算法分类模型的准确性和稳定性。

3 算法进阶分析 3.1 测试准确率

根据机器学习算法的特点，第2章节中所述的算法的准确率实为“训练准确率”，当训练准确率过高时，很可能是因为发生了过拟合现象。为判断算法是否存在过拟合现象，并衡量它们判别效果，利用训练好的分类模型(模型训练集见表 6，模型参数见表 7)对训练集外的已知样品类别的182个玄武岩样品(包含55个MORB，60个OIB，67个IAB)进行测试，测试结果见表 10。

由表中结果可得，KNN对IAB的判别准确率最高，RF对OIB和MORB的分类效果最佳。总的来看，RF的准确率最高，达到了88.46%，即对于一个新的样本，RF将其分类正确的概率可达88.46%，其效果远超于上文所述的任何一个判别图。四种智能算法分类测试结果从优到劣排序如下：RF＞SVM＞NB＞KNN。与第2章节中KNN分类训练效果优于NB有所不同，NB测试准确率要高于KNN。这说明智能算法训练、测试结果的非一致性，而通常来讲，测试准确率是真正能反映一个算法能力的指标。

3.2 后验概率计算——以RF为例

从本质上来说，无论是训练准确率还是测试准确率，都属于“分类准确率”，即对于一个已知类别的样本，算法将其正确归类的概率，这也是目前机器学习领域所关注的主要问题之一。然而，算法对于一个未知类别的样本的分类结果有多大的可信度，却极少有人去深究。本文从这一角度出发，利用贝叶斯定理，对这一问题做了进一步探究。

贝叶斯定理可表述为：假设事件B₁, B₂, …, B_n是样本空间Ω的一个划分，P(B_i)＞0(i=1, 2, …, n)，A是任一事件且P(A)＞0，则存在以下关系(盛骤, 2001; 李航, 2012)：

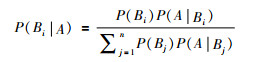
(6)

上述公式又被称为“逆概公式”，根据该公式，将3.1节RF测试结果进行“反推”，以求得分类模型判别为某一样品类别下的后验概率。RF算法对于测试集的详细判别结果如表 11所示，可以看出，当RF算法判别一个未知样品为IAB、OIB或MORB时，其可信度分别为94.74%、90.47%和80.22%。

3.3 数据缺失——鲁棒性验证

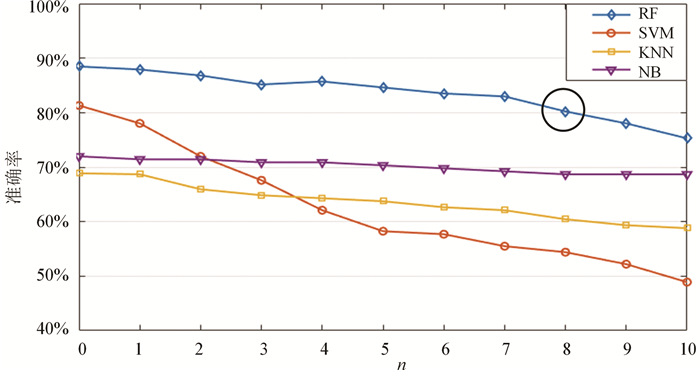
对于每个样品中的化学成分，在测量过程可能会有数据丢失，因此有必要验证四种智能算法在数据缺失情况下的鲁棒性。统计发现，对于每一个样本，其51个特征中平均约有22个特征值为0。原因是有些元素在某些样本是不存在的，或者是因为记录遗失。在测试集中，将每一个向量中的非零成份中的任意的n(n取1~10)个成份设置为0，人为地制造数据缺失，并以此测试算法的分类准确率，测试结果如图 7所示。图 7直观体现出以下几点：(1)缺失数据达8个时，RF算法仍有80%以上的分类准确率；(2)SVM算法受数据缺失的影响较大；(3)KNN算法受数据缺失影响较小，但整体的准确率一直较低；(4)缺失数据在在10个以内，NB算法几乎不受影响。从数据缺失时的模型的整体效果来看，RF是应该被优先采用的算法。另外，考虑到NB算法在鲁棒性上表现卓越，如果可以结合专业知识提升其整体准确率，该算法亦可被优先考虑。

3.4 特征重要性分析

与传统的统计分析相比，智能算法有着准确率高但解释性差的缺点。尤其以神经网络、SVM为代表的智能算法，一直以来被统计学家们诟病为“黑箱”算法，即它可以给出一个很好的结果，但无法对这个结果做出专业性的解释。而随机森林算法作为一个相对较新的算法，在对结果的解释方面有其独特的优势。由于随机森林本质上是一定数量的决策树的集合，当训练过程结束后，通过提取每一个决策树并统计它们的所有的节点信息，我们可以总结出样本的各个特征的重要性程度，如表 12所示。

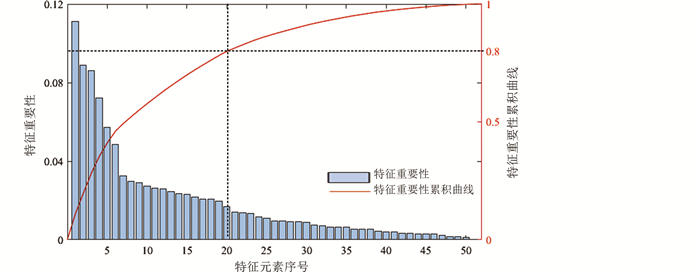
根据表 12中特征的重要性，制作帕累托图(Wilkinson, 2006)，如图 8所示。可将所有特征元素分为三类：主要特征(累积重要性范围为0%~80%)、次要特征(累积重要性范围为80%~90%)和一般特征(累积重要性范围为90%~100%)。由图可知，主要特征为前20个特征，代表这些特征在判别过程中起到了超过80%的作用。其中，对判别结果贡献最大的主量元素为TiO₂、SiO₂、Al₂O₃、P₂O₅、MgO、CaO和K₂O含量，这与当前流行的判别图所采用的元素相似；对判别结果贡献最大的微量元素为Sr、Zr、Ba、Nb、Nd、Ni、Rb、Cr、La、Eu、Y和Sm的含量，其中Sr、Zr、Nb和Ni为微量元素判别图中常用的元素；对判别结果贡献最大的同位素比值为²⁰⁶Pb/²⁰⁴Pb。另外注意到常用于微量元素判别图的Y元素在20个元素中重要程度相对较低，而Ba元素则对判别结果有着较大的影响，因此可以考虑在传统的分析中提高对Ba元素的重视。

4 结论

本文将NB、KNN、SVM以及RF四种智能算法应用于解决玄武岩构造环境判别这一问题，并与传统的判别图解法在判别正确率、结果稳定性等方面进行比较。以此为基础，选用训练样本外的测试集，通过对智能算法作后验概率计算、鲁棒性验证、特征重要性排序等进阶分析，结果表明智能算法在MORB、OIB和IAB三类玄武岩判别方面优势明显，主要表现为：(1)利用智能算法判别大地构造环境，分类快速、准确度高，且鲁棒性较强，在缺失部分数据的情况下仍可做出准确判别；(2)综合考虑分类准确性、可靠性和鲁棒性等方面，本次研究认为选择RF和NB算法作为三类玄武岩判别模型更为合适；(3)应用贝叶斯公式求解逆概率，实现“由果及因”的合理推断，进一步提高了智能算法在岩石构造环境判别方面的实用性；(4)可通过特征重要性分析发现对判别效果影响最大的元素，减少传统分析方法的盲目性，并可以为传统的分析方法提供参考。

然而，本文仍存在诸多不足，例如智能算法较判别图解法而言，对样本数据的可解释性较弱，需考虑如何对玄武岩化学成分作科学合理的解释，另外，还需考虑如何对玄武岩做进一步种类细分等，上述展望将在后续研究中作为重点内容进行探讨。

致谢      本文工作在“第二届全国大数据与数学地球科学学术研讨会”得到了展示，在与中国科学院地质与地球物理研究所张旗、中山大学周永章、中国地质调查局发展研究中心朱月琴等多位专家的讨论中获得了诸多宝贵建议和意见，在此表示感谢。