岩石学报  2012, Vol. 28 Issue (8): 2656-2666   PDF    
引用本文
卫清, 段振豪, 毛世德. 2012. H2O-CO2-NaCl体系石英溶解度模型 (适用于高达1000℃、1.5GPa的高温高压环境). 岩石学报, 28(8): 2656-2666  
WEI Q, DUAN ZH and MAO SD. 2012. A thermodynamic model of quartz solubility in H2O-CO2-NaCl systems up to 1000℃ and 1.5GPa. Acta Petrologica Sinica, 28(8): 2656-2666(in Chinese with English abstract)   
H2O-CO2-NaCl体系石英溶解度模型 (适用于高达1000℃、1.5GPa的高温高压环境)
卫清1, 段振豪1, 毛世德2     
1. 中国科学院地质与地球物理研究所地球深部研究重点实验室, 北京 100029;
2. 中国地质大学地球科学与资源学院, 北京 100083
2011-08-16 收稿; 2011-11-30 改回.
基金项目: 本文受国家自然科学基金项目 (90914010、41020134003、40873050) 资助
第一作者简介: 卫清, 女, 1983年生, 博士生, 计算地球化学专业, E-mail: veronica.lily@163.com
摘要: 石英在热水溶液中的溶解度对地球化学和岩石学的研究都极为重要。我们提出一个能够适用于H2O-CO2-NaCl复杂流体成分, 高温高压 (0~1000℃, 0~1.5GPa) 条件下的石英溶解度计算模型, 形式如下： 其中A(T)、B(T)、C(t) 均为温度T(K) 和t(℃) 的多项式。xH2O和V*H2O分别代表流体中水的摩尔分数和有效偏摩尔体积。V*H2O值由公式Vmix=xHOV*H2O+ΣxsVs计算得到。其中, Vmix代表流体混合物的摩尔体积, 由Mao et al.(2010) 的最新模型计算得到, xs和Vs分别代表溶质的摩尔分数和本征体积。具体采用VCO2=29.9cm3/mol、VNaCl=30.8cm3/mol。本模型精度较前人模型有所提高, 并且适用深达下地壳的温度-压力-成分环境, 如：巴罗式变质带、板块俯冲带等。另外, 本模型可被用于建立石英地质温度计, 加深人们对于石英脉及有关矿床成因的认识, 并且可用来指导实验及工程。本模型的在线计算程序可通过以下网站获得：www.geochem-model.org。
关键词: 石英溶解度     高温高压     H2O-CO2-NaCl流体     计算模型    
A thermodynamic model of quartz solubility in H2O-CO2-NaCl systems up to 1000℃ and 1.5GPa
WEI Qing1, DUAN ZhenHao1, MAO ShiDe2     
1. Key Laboratory of the Earth’s Deep Interior, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
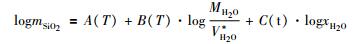
2. School of Earth Sciences and Resources, China University of Geosciences, Beijing 100083, China
Abstract: There are numerous experimental measurements of quartz solubility has been studied over a broad spectrum of aqueous fluid compositions and temperature-pressure range. Here, we proposed an equation, which can calculate the solubility of aqueous silica in H2O-CO2-NaCl fluid mixture at high temperatures and high pressures from 0~1000℃ and 0~1.5GPa, as follows: Here A(T)、B(T) and C(t) are polynomials of temperatures T(K) and t(℃), xH2O and V*H2Ostand for the mole fraction and effective partial molar volume of H2O in fluid, respectively. The value of V*H2O is calculated from the relation Vmix=xHOV*H2O+ΣxsVs, where Vmix represent the molar volume of the fluid mixture, which is calculated from the recent model of Mao et al.(2010), xs and Vs denote the mole fraction and the intrinsic volume of the solute, respectively. Values VCO2=29.9cm3/mol and VNaCl=30.8cm3/mol were adopted by this thermodynamic model. The accuracy of our model is better than previous models, and our model is able to predict the solubility of quartz over a much wider T-P-xs conditions relevant to the deep crust, so that it could be used to evaluate aqueous silica transport in Barrovian metamorphic belts and subduction zones and so on. In addition, our model is helpful to establish quartz geothermometer, discover the formation mechanics of deposits relevant to the quartz veins. Online calculation of the solubility of quartz is available on: www.geochem-model.org.
Key words: Quartz solubility     High temperatures and high pressures     H2O-CO2-NaCl fluid mixture     Thermodynamic model    
1 引言

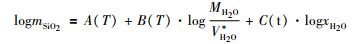
石英在地壳中广泛存在。其主要成分由岩石圈丰度最高的前两种元素氧和硅组成。在地壳以及更高的温度压力范围内, 石英的溶解-沉淀行为是水热流体中硅酸盐迁移量的主要制约因素之一。另外, 石英在含盐含气水溶液中的溶解度对地球化学及岩石学的研究都至关重要 (Manning, 1994)。研究石英在热水溶液中的溶解行为, 能够加深人们对硅质岩及石英脉和有关矿床成因的认识, 并且, 在海洋生物学、地热能开发、采油工程、石英地质温度计的建立、石英在热水溶液中的反应速率和反应机理以及其他涉及天然水体的学科与工程技术中, 石英溶解度的资料也具有十分重要的价值 (张生和李统锦, 1997)。

基于石英溶解度的重要性, 实验学家和理论学家开展了大量研究工作。如自1950年起, Kennedy等学者便开始测量石英在纯水中的溶解度 (Kennedy, 1950；Morey and Hesselgesser, 1951；Khitarov, 1956；Kitahara, 1960；Fournier, 1960；Morey et al., 1962；Siever, 1962；Weill and Fyfe, 1964；Anderson and Burnham, 1965；Crerar and Anderson, 1971)。Walther and Helgeson (1977)对以上早期研究进行了系统的回顾。Manning (1994)的研究将实验温度压力范围升高至1000℃, 2GPa的高温高压环境。Khitarov (1956)等人首次发表了石英在H2O-NaCl、H2O-CO2-NaCl水热体系中溶解度的测量结果，之后又有许多学者致力于石英在混合体系中溶解度的研究 (Khitarov, 1956；Kitahara, 1960；Van Lier et al., 1960；Anderson and Burnham, 1967；Ganeyev, 1975；Novgorodov, 1977；Hemley et al., 1980；Fournier et al., 1982；Fournier, 1982；Xie and Walther, 1992；Newton and Manning, 2000；Shmulovich et al., 2001, 2006；Foustoukos and Seyfried, 2007)。

虽然前人开展了大量石英溶解度的实验工作, 但是, 由于实验数据的离散性, 给研究人员的应用带来了很大不便。因此, 理论学家期望建立石英溶解度的计算模型, 这样的模型不仅能够重现宽广温度-压力-成分空间内的众多实验数据点, 而且能够预测实验温度压力范围以外的石英溶解度。早期的理论学家提出了不少石英溶解度的计算模型 (Jasmund, 1952；Mosebach, 1957；Wasserburg, 1958；Walther and Helgeson, 1977；Fournier and Potter, 1982；Fournier, 1982；Mckenzie and Helgeson, 1984；Walther and Schott, 1988；Shock et al., 1989；Von Damm et al., 1991)。但是, 这些模型要么精度欠佳, 要么就是适用的温度压力范围有限。Manning (1994)依据其本人新测量的高压条件下石英溶解度数据, 成功提出了适用于25~900℃、1bar~10kbar条件下石英在纯水中溶解度的计算模型。最近Akinfiev and Diamond (2009)的研究工作, 将石英溶解度的计算模型拓展到含盐含气混合流体体系。虽然Manning (1994)的模型提升了适用的温度压力范围, 但是其模型只适用于纯水体系, 不能客观地描述石英在天然流体中的溶解行为。Akinfiev and Diamond (2009)虽然提出了石英在纯水及含盐含气混合流体中溶解度的计算模型, 但其精度还有待提高。通过系统地回顾前人研究工作, 这里, 我们期望得到一个形式简单, 精度更高、温度压力适用范围更加广泛的通用型石英溶解度计算模型。

2 石英溶解度计算模型的发展

为获得精确且具一定外延性的石英溶解度计算模型, 理论学家首先确定石英在纯水中的溶解方程, 然后说明盐及挥发性气体对石英溶解度的影响, 进而固定参数形式, 以得到一个宽广温度 (达1000℃)、压力 (达1.5GPa) 及成分 (相当于地壳组成) 条件下能够精确描述石英溶解度的经验方程。

2.1 纯水中石英溶解度计算模型

了解石英在纯水中的溶解度, 是研究其在富含CO2等挥发性物质及溶解的矿物组分, 特别是地壳卤化物等天然流体中溶解行为的基础。现代水热地球化学对水合物热力学性质的描述, 主要有静电学模型 (Ryzhenko, 1981) 和密度模型 (Anderson et al., 1991) 两种形式。这两种模型都可用来描述石英的溶解问题。

静电学模型反映了溶解的水合物与周围溶剂H2O分子之间的静电相互作用。石英矿物的溶解基于以下平衡反应：

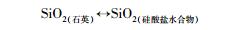
(1)

这里硅酸盐水合物, SiO2(硅酸盐水合物)的性质并不依赖溶解的硅酸盐的外部结构。根据HKF方程 (Helgeson et al., 1981), 水化离子j的化学位可由博恩方程 (Born, 1920) 给出：

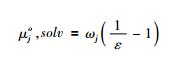
(2)

其中, ε表示溶剂的介电常数, ωj为第j项水合物的绝对博恩系数。Walther and Helgeson (1977)根据方程 (1), 回归石英溶解度实验数据, 得到硅酸盐水合物的绝对博恩系数ωSiO2(aq)=0.1291×105cal·mol-1。后来, Shock et al.(1989)等根据新的HKF状态方程 (Tanger and Helgeson, 1988), 回归溶解度实验数据, 得到了硅酸盐水合物SiO2(aq)的全套状态参数。当水的密度小于1g/cm3时, 计算的H2O的介电常数是可信的。但是, 由于缺少更高水密度下石英溶解度的实验数据, 以及缺乏足够的具有预测性的模型, HKF模型很难用于超过5kbar的条件。

另一类密度模型则主要基于经验观测。早在1956年, Franck等 (Franck, 1956, 1961；Quist, 1970；Marshall and Mesmer, 1984；Mesmer et al., 1988, 1989) 就发现, 在一定的压力范围内, 在固定温度下, 电离的水分子与其它水合物质的logK值与以10为底的纯水密度对数值成线性关系 (图 1)。因此, 对于石英的溶解反应方程 (1), 其反应平衡常数K的参数化形式可由下式表示：

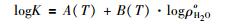
(3)
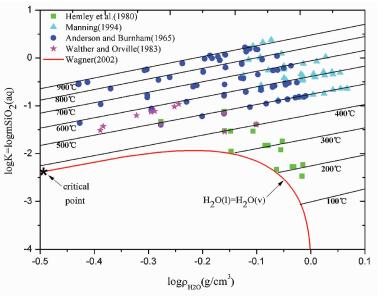
图 1 等温条件下石英在纯水中的溶解度logmSiO2与log ρH2O的关系 图标■、▲、●、★代表实验数据点, *代表H2O的临界点, 曲线代表H2O的饱和蒸汽压, 由Wagner and Pru (2002)方程计算得到, 直线代表等温条件下本模型计算的石英溶解度 Fig. 1 logmSiO2 vs. logρH2O for experimental studies of quartz solubility at the same temperature in pure water Symbols ■, ▲, ●, ★ represent experimental data, * is critical point of H2O; the curve refers to the saturation vapor pressure of H2O, which is calculated after Wagner (2002), and the solid lines are logmSiO2 calculated from this model

这里, A(T)、B (T)为温度 (K) 的多项式, logρoH2O代表以10为底的纯水密度对数值, 单位为g/cm3。如果ρoH2O已知, 并且与logK线性相关, logK便只是温度T(K) 和水密度ρoH2O的函数, 这使得方程 (3) 成为计算高温高压条件下水合物化学位等热力学性质的理想选择。但是, 比起静电学模型, 由于logK与logρoH2O之间的物理关系还无法解释, 密度模型仍然缺乏物理层面的可信证据 (Akinfiev and Diamond, 2009)。根据溶解反应方程 (1), Fournier and Potter (1982)以及Manning (1994)都依据获得的石英溶解度数据, 进行了密度模型的回归分析。Manning (1994)给出的多项式 (如公式 (4) 所示) 不仅简单精确, 而且适用于更高的温度压力范围 (25~900℃, 1bar~10kbar)。

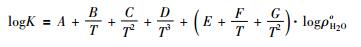
(4)

上式中A至G均为回归系数, logK即logmSiO2。

2.2 混合流体中石英溶解度计算模型

虽然静电学模型能够重现石英在H2O-非极性气体二元混合物中的溶解度数据 (Walther and Orville, 1983；Xie and Walther, 1993；Akinfiev and Zotov, 1999), 并且能够拓展到H2O-盐体系 (Akinfiev and Zotov, 1999) 溶解度的计算。但是在极端条件下, 静电学模型预测结果与实验数据出现较大偏差。如在高温高压 (800℃, 1000MPa) 条件下, 石英在H2O-非极性气体二元体系中溶解度模型预测与实验数据不一致 (表 1)；并且该模型不能重现低压水盐体系中的实验数据 (Akinfiev and Diamond, 2009)。由表 1可见, 相比实验数据, 静电学模型严重低估了石英在H2O-CO2混合流体中的溶解度, 而本文提出的密度模型, 则较好地重现了石英的溶解度。

表 1 石英在H2O-CO2混合物中溶解度实验与模型预测比较 (800℃, 1000MPa) Table 1 Comparison of experimental and predicted quartz solubilities in H2O-CO2 mixtures (800℃, 1000MPa)

由于静电学模型的上述局限性, Fournier (1983)修正了石英在纯水中溶解度计算的密度模型, 提出以下方程, 计算石英在NaCl水溶液中的溶解度。

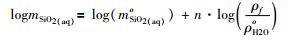
(5)
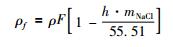
(6)

其中, mSiO2(aq)o为石英在纯水中的溶解度；ρf代表自由水的密度, 如那些远离盐离子水合层的水分子密度；ρoH2O表示纯水密度；ρ为溶液密度；F代表溶液中H2O的质量分数；h为盐的平均水合数。

石英在含盐含气混合流体中的溶解反应式为：

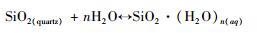
(7)

其中, n为硅酸盐水合物的溶剂化值。因此, 方程 (7) 的平衡常数K*可表示为：

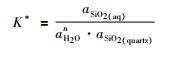
(8)

对方程 (8) 两边同取以10为底对数：

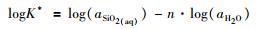
(9)

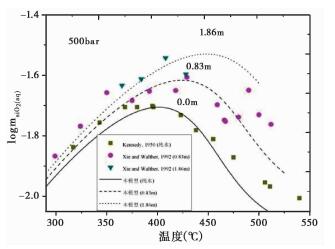
如果近似地取aSiO2(aq)=mSiO2(aq), 并且忽略形成硅酸盐水合物所结合的H2O的摩尔分数, 假设aH2O=xH2O, 上式变为：

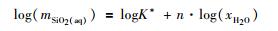
(10)

从以上方程我们可以看出, SiO2的溶解度会随着水的摩尔分数的下降而下降, 这与高盐度时观测到的“盐析”现象一致 (详见下文)。方程 (9) 也构成了Fournier (1983)密度模型的基础。虽然该密度模型很好地描述了石英在H2O-NaCl体系中的溶解度, 但是认为自由水的密度, ρf, 与水的摩尔分数, xH2O, 成比例, 仍然缺乏物理层面的解释。并且, 据推测, 水合数h应该是温度、压力、盐含量的复杂函数, 而在Fournier (1983)用于计算石英溶解度的方程中, 却将水合数设为零 (Akinfiev and Diamond, 2009), 这就使Fournier (1983)的密度模型还有待改进的空间。

3 本模型及其参数化

建立本模型的目的在于提出一个简单且具一定外延性的理论方程, 进而描述广泛温度、压力以及流体成分条件下石英的溶解行为。这里所说的简单是指模型只有少数几个参数。减少参数不仅使参数更具物理意义, 进而理解溶解现象的本质, 而且使模型在超出实验数据的范围内具有预测效果。另外, 对于将石英在纯水中的溶解方程拓展到含盐含气水溶液而增加的修正项, 本模型给出了关于温度t(℃) 的二次项形式。这些改变, 都使得本模型在保证预测性和精度的条件下, 能够计算石英在一宽广温度、压力范围内 (适用的温压上限达1000℃, 1.5GPa), 在包含水-气-盐等多组分混合流体中的溶解度。

通过对石英溶解度研究工作的系统回顾, 我们尽可能地搜集了本研究领域的实验数据。不仅包括众多早期数据 (Van Nieuwenburg and Van Zon, 1935；Kennedy, 1950；Van Lier et al., 1960；Morey et al., 1962；Siever, 1962等), 也涵盖了最近发表的的实验数据 (Newton and Manning, 2008；Manning et al., 2010；Davis et al., 2011)。大量实验数据 (表 2) 的回归, 使得本模型在保证外延性的基础上, 精度比前人模型有所提高。

表 2 石英溶解度的实验测量 Table 2 Experimental measurements for quartz solubility

本模型以Fournier (1983)密度模型为基础, 采用方程 (4)(Manning, 1994) 的形式计算石英在纯水中溶解度。假设硅酸盐的溶解度主要受周围水分子的短距离相互作用控制, 而溶解的其它水合物质的影响可以忽略 (Akinfiev and Diamond, 2009), mSiO2(aq)值将取决于流体水分子间的平均距离。另外, 通过分析logmSiO2与温度的关系 (图 2) 可见：在固定的压力下, 纯水及含盐流体中石英溶解度的对数值, logmSiO2, 随温度变化呈现先增大后减少的规律。因此, 本模型应用到混合流体中的修正项采用温度 (℃) 的二次多项式。

图 2 纯水及含盐流体中石英溶解度对数值与温度 (℃) 关系图 (500bar) 图中曲线为本模型在纯水及0.83m、1.86m NaCl水溶液中石英溶解度的计算结果, 图标代表实验数据点, 其中, ■(纯水), 为Kennedy (1950)实验数据, ●(0.83m) 以及▼(1.86m) 为Xie and Walther (1992)实验数据 Fig. 2 Logarithm of molality of SiO2(aq) for quartz solubility as a function of temperature (℃) in pure water and NaCl solutions (500bar) The curve is this model calculated quartz solubility in pure water and in 0.83m, 1.86m NaCl solutions. The symbol refers to the experiment data points, ■(pure water), Kennedy (1950), ●(0.83m) and ▼(1.86m) Xie and Walther (1992)

据以上分析, 本文提出模型的主方程形式为：

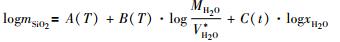
((11))

其中, A(T), B(T), C(t) 分别是关于开尔文温度 (K) 及摄氏温度 (℃) 的多项式。A(T), B(T) 采用方程 (4) 的形式 (Manning, 1994), MH2O、xH2O分别为水的摩尔质量和混合流体中水的摩尔分数；V*H2O作为一个新参数, 被定义为H2O的有效偏摩尔体积。对于H2O的有效偏摩尔体积V*H2O, 我们通过Mao et al.(2010) 提出的最新模型求取混合物的摩尔体积, Vmix, 继而据式 (12) 确定H2O的有效偏摩尔体积V*H2O。

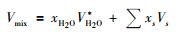
(12)

其中, Vmix为流体混合物的摩尔体积 (单位：cm3/mol), xs和Vs分别表示溶质的摩尔分数和本征体积。例如：对于二元混合物, 溶质的摩尔分数xs=1-xH2O, 因此, 混合物的摩尔体积可写作：

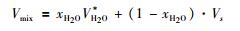
(13)

根据Akinfiev and Diamond (2009)对CO2-H2O及NaCl-H2O体系石英溶解度实验数据的回归分析结果, 本模型亦采用VCO2=29.9cm3·mol-1, VNaCl=30.8cm3·mol-1分别作为CO2和NaCl的本征体积, 继而据式 (12), 求取V*H2O。这里, 将C(t)也写成关于温度T(K) 的二次多项式：

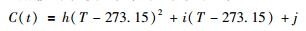
(14)

通过回归石英在H2O-CO2-NaCl三元混合流体中溶解度的大量实验数据, 本文最后确定A (T)、B (T) 的系数A, B, C, D, E, F, G以及C(t) 的系数h, i, j详见表 3。

表 3 模型参数 Table 3 The parameters of this model

根据前文所述, 在一定的压力范围内, 在固定温度下, 电离的水分子与其它水合物质的logK值与以10为底的纯水密度成线性关系 (Franck, 1956, 1961；Quist, 1970；Marshall and Mesmer, 1984；Mesmer et al., 1988, 1989), Fournier (1983)又提出了石英在含盐水溶液中溶解度的密度模型, 最新的密度方程又使得石英在含盐含气混合流体中溶解度的计算成为可能 (Akinfiev and Diamond, 2009)。因此, 根据水分子及水合物logK值与水密度logρH2O之间的线性关系, 只要能够精确求得混合流体中水的有效偏摩尔体积V*H2O, 便可确定石英在含盐含气流体中的溶解度 (混合流体中的水密度据logρH2O=log 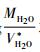求得)。对于水的有效偏摩尔体积, V*H2O的求取, 本模型根据Mao et al.(2010) 提出的最新计算水-气-盐混合体系摩尔体积Vmix的模型求得 (计算过程见方程 (12))。Mao et al.(2010) 提出的这一最新求取混合流体单相PVTx的模型, 在273~1273K、1~5000bar的温度压力范围内, 不仅具有较高的精度, 同样具有较好的外延性。如表 4所示, 该模型能够成功预测H2O-CO2-NaCl混合流体为数不多的几个高温高压实验点 (Johnson et al., 1992), 模型预测与实验测量的相对偏差不超过3%。这也为本模型成功外延至1000℃, 1.5GPa的高温高压环境创造了可能。

表 4 Mao et al.(2010) 模型高温高压条件下H2O-CO2-NaCl混合流体摩尔体积的预测 Table 4 Prediction of mole volume of H2O-CO2-NaCl mixture fluid at high temperatures and high pressures by Mao et al.(2010)
4 模型有效性检验

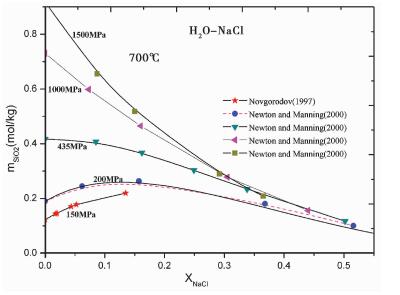
至此, 根据以上分析, 我们提出的这一用来计算石英在含盐含气混合流体中溶解度的密度模型, 只包含温度 (K)、水的有效偏摩尔体积V*H2O、及水的摩尔分数xH2O三个参数。减少参数不仅方便使用, 其优点亦如前文所述。相对于Akinfiev and Diamond (2009)最近提出的石英溶解度模型, 由于对实验数据做了系统的回顾与总结, 并采用新的模型 (Mao et al., 2010) 求取H2O-CO2-NaCl三元体系混合物的摩尔体积, 以及在形式上对前人模型做了修正, 本模型精度有所提高。本文提出的模型不仅能够重现Manning (1994)之前的大量实验数据, 对1994年之后新获得的数据也能较好地模拟, 并且可以外延到部分没有实验数据的温度压力空间。比起纯水, 石英在混合流体, 特别是盐水中的溶解行为更加复杂。对于盐水中石英溶解度复杂变化的情况, 本模型亦能准确描述。如图 3所示, 在700℃时, 在超过435MPa的高压条件下, 石英溶解度均随着盐度的增加而降低, 而当压力下降到约200MPa时, 适量的盐的加入 (约0.1XNaCl), 石英溶解度呈现非单调变化, 即：溶解度先升高, 后降低, 在NaCl含量约0.1XNaCl附近出现峰值, 低盐度 (盐的摩尔分数XNaCl＜0.1时) 时的“盐溶”效应 (盐的加入增加了石英溶解度) 逐渐转变为高盐度的“盐析”(盐的加入降低了石英溶解度) 效应。图 3中实线表示实验数据的变化趋势, 以200MPa处虚线代表的本模型模拟情况为例, 说明在实验温度、压力、盐度条件下, 对于存在这种由“盐溶”-“盐析”突变的有关石英溶解度复杂变化的情况, 与图中实线代表的实验趋势曲线相比, 虚线表示的模型模拟情况, 符合实验误差, 较好地描述了这种复杂现象。

图 3 石英在H2O-NaCl溶液中溶解度 (以mSiO2值表示) 与盐的摩尔分数关系图 (700℃, 等压条件) 图中离散的点为实验数据, 实线为实验数据的示意曲线, 虚线是本模型模拟情况 Fig. 3 Quartz solubility (expressed as mSiO2) in H2O-NaCl solutions vs. mole fraction of NaCl at 700℃ and on isobars Symbols in the picture correspond to the experimental data. Solid lines represents sketch curves of experimental data points, and dashed line is the curve predicted by this model

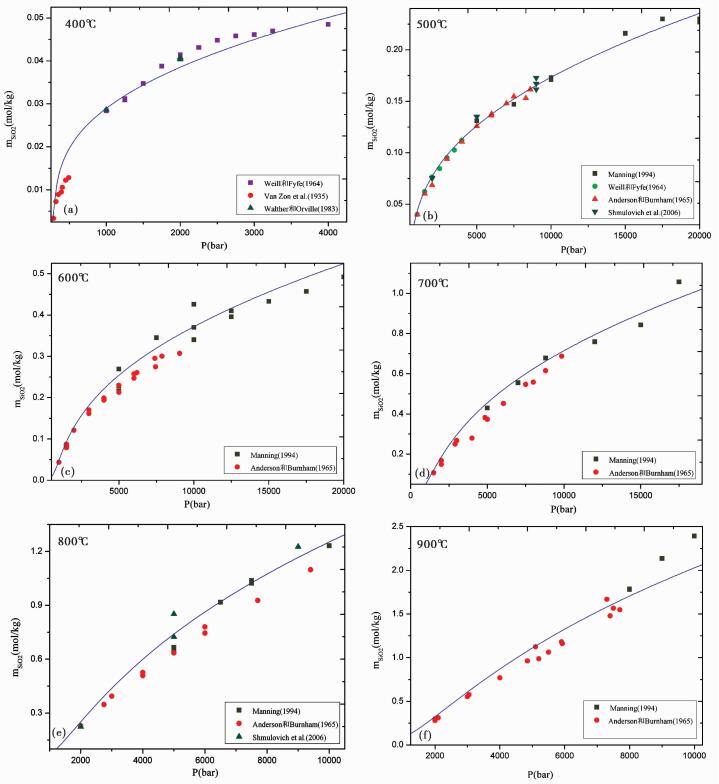
通过与实验数据比较 (图 4), 可以看出, 石英在纯水中的溶解度随温度的升高而升高 (如图 4b-f中横坐标均为5000bar处的石英溶解度, 以SiO2的质量摩尔浓度mSiO2表示, 由约0.125m逐渐升高至1.0m), 随着压力的增加而增加。本模型能够很好的重现纯水中的实验数据, 并且在高温高压 (700℃, 1.5GPa) 条件下, 模型也具有较好的预测效果。

图 4 不同温度下, 压力区间内石英在纯水中溶解度实验数据与模型预测比较 图标为各实验数据点, 曲线为模型预测结果 Fig. 4 Comparison experimental data points and this model with quartz solubility in pure water at different temperatures and within different pressure regions Symbols are experimental data points, and the curve is this model prediction

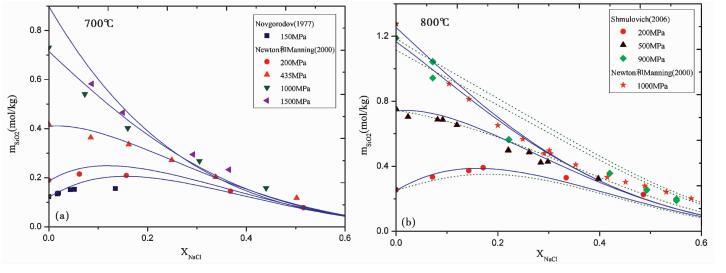
图 5作为模型预测的结果, 显示出了含盐流体中石英溶解行为的复杂性。由图 5可见, 在高温 (700℃、800℃) 和超过200MPa的超临界盐水中, 石英溶解出现明显的“盐析”现象, 并且随着压力的降低, 这种效应逐渐减缓, 似乎是在为更低压力条件下时出现的“盐溶”效应做准备。如前文所述, 在200MPa时, 石英在H2O-NaCl体系中的溶解度呈现非单调变化, 表现为溶解度先升高, 后降低。NaCl能显著提高石英溶解度的前提条件是：纯水具有低的密度 (见200MPa等压线)。此作用的合理解释为：硅酸盐水合物的行为主要受它外围水分子的短距离相互作用控制。低水密度时, 盐的加入, 引起一个可见的流体体积收缩 (Anderko and Pitzer, 1993), 降低了相互作用分子的平均距离, 提升水合作用, 进而增加SiO2的溶解度。此作用与纯水中等温升压的效果类似。而在高密度的水中加入NaCl, 则扩张了H2O-SiO2二元混合物的摩尔体积 (Anderko and Pitzer, 1993), 因此增加了水分子间的平均距离, 降低水合作用, 进而减少SiO2的溶解度。NaCl之所以能改变溶液的体积, 是因为它是一种电解质, 它的电解及水合程度均是温度、压力以及浓度的可变函数。

图 5 700℃、800℃时石英在H2O-NaCl混合流体中的溶解度 图标代表固定压力下的实验数据, XNaCl=0时的实验数据采用Manning (1994)数据.虚曲线为Akinfiev and Diamond (2009)的模型预测结果, 实曲线代表本模型的模拟情况.其中, NaCl的本征体积, 采用VNaCl=30.8cm3/mol(Akinfiev and Diamond, 2009) Fig. 5 Quartz solubility in H2O-NaCl mixture fluids at 700℃ and 800℃ Symbols indicate experimental data at specified pressures. The experimental data points at XNaCl=0 use Manning (1994). Dashed curves are density model of Akinfiev and Diamond (2009). Continuous curves are predictions of our model and with intrinsic volume of NaCl, VNaCl=30.8cm3/mol(Akinfiev and Diamond, 2009)

图 5中的实曲线为本模型的模拟结果。我们看到, 在高温高压的极端条件下, 本模型成功重现了实验数据的变化趋势, 并且精度符合实验误差。对比Akinfiev and Diamond (2009)的最新模型 (图 5b中虚曲线所示), 本模型在中低盐度 (XNaCl < 0.4) 的条件下能够更好地重现实验数据, 并且在高温高压 (800℃, 900MPa、800℃, 1000MPa) 时具有明显优势。当盐度较高时 (XNaCl>0.4), 本模型存在一定系统偏差, 低估了石英的溶解度。这可能由高压条件下, NaCl易于水解, H2O-NaCl体系的状态方程过高估计了混合物的摩尔体积Vmix所致。

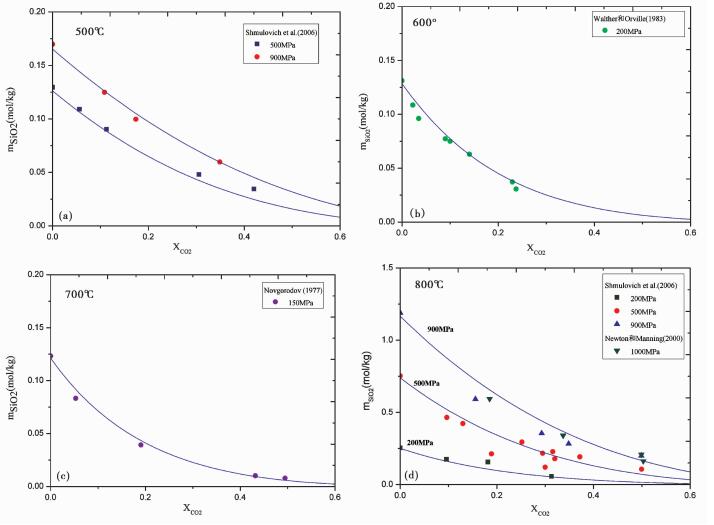
图 6显示了本模型对H2O-CO2体系中石英溶解度的预测结果。如图 6所示, 在500~800℃、150~1000MPa的温度压力区间内, CO2的加入无一例外的引起了石英溶解度的下降, 出现明显的“盐析”现象。这可能是由于CO2是非电解质, 加入CO2总是扩大流体体积, 进而降低水解, 降低石英的溶解度。由图可见, 当温度小于800℃时, 本模型在实验误差范围内很好地重现了实验数据。而在高温 (800℃) 高压 (900MPa以上) 的极端条件下, 本模型高估了实验值。

图 6 500℃、600℃、700℃、800℃条件下, H2O-CO2体系中石英溶解度模型预测与实验数据的比较 图标代表实验数据, XCO2=0时石英溶解度采用Manning (1994), 图中曲线代表本模型.对于CO2的本征体积采用VCO2=29.9cm3/mol(Akinfiev and Diamond, 2009) Fig. 6 Comparison experimental data points and the prediction of this model of quartz solubility in H2O-CO2 fluid at 500℃, 600℃, 700℃ and 800℃ Symbols are experimental data points, the experimental data points at XCO2=0 use Manning (1994). Curves are predictions of our model with intrinsic volume of CO2, VCO2=29.9cm3/mol(Akinfiev and Diamond, 2009)

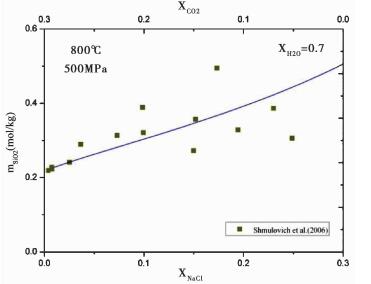
对于石英在更为复杂的H2O-CO2-NaCl三元混合流体中的溶解度, 目前只有Shmulovich et al.(2006) 做过相关实验研究。如图 7所示, 本模型的计算结果落在实验数据之间, 表明本模型能够合理地预测混合流体中石英的溶解度。由于实验数据的缺乏, 本模型对复杂体系的预测精度还有待进一步的验证。

图 7 800℃、500MPa条件下, 水的摩尔分数XH2O=0.7时, 石英在H2O-CO2-NaCl三元混合流体中的溶解度 NaCl的摩尔分数XNaCl, 和CO2的摩尔分数XCO2, 呈相反的变化趋势, 总量为0.3.图标代表实验数据, 曲线为本模型的计算结果.CO2和NaCl的本征体积分别采用VCO2=29.9cm3/mol和VNaCl=30.8cm3/mol (Akinfiev and Diamond, 2009) Fig. 7 Quartz solubility in ternary H2O-CO2-NaCl fluids at 800℃ and 500MPa with XH2O=0.7 The values of XNaCl and XCO2vary inversely, their sum equal to 0.3. Symbols indicate experimental data points, and the curve is the predication of this model with the intrinsic volume of CO2 and NaCl are VCO2=29.9cm3/mol and VNaCl=30.8cm3/mol
5 模型应用

本文提出的这一石英溶解度计算模型, 不仅精度符合实验误差, 适用于高温、高压复杂的含盐含气混合流体, 在地质和实际工程等领域也有诸多应用。如：石英可作为地质温度计, 利用泉口或井孔地热流体的SiO2饱和浓度, 计算地下热流体平衡带的温度, 即, 利用泉口SiO2的浓度, 计算储库基底温度。对于野外常见的石英脉、方解石脉等这种流体迁移的通道, 作为重要的脉石矿物, 石英溶解度的相关资料, 对成矿流体迁移、沉淀以及与相关元素富集成矿也具有重要参考价值。如：SiO2的存在, 明显有利于Sb的溶解, 并以Sb-Si络合物的形式存在, 使得Sb在低温贫硫富硅的热液流体中溶解、迁移 (樊文苓等, 1997)。另外, 前人研究认为, 胶体SiO2和Au粒对Sleeper矿床富矿石中产生富金条带是很重要的。原生SiO2的性质和Ag矿、Au矿沉淀物的识别及其沉淀期后结晶史对于了解Sleeper矿床富矿脉内Au的沉淀过程极为重要 (Saunders, 1995)。在石油工程等相关领域, 石英溶解度也具有很重要的实际应用价值。如：井下石英颗粒的变化情况, 对稠油储层具有一定影响。结果表明, 石英在强碱溶液中的溶解度, 与温度及PH值呈指数规律变化。这对于正确了解稠油储层在热采过程中的孔隙结构变化、次生乳隙的产生、岩石骨架的破坏, 低温冷凝前缘硅化的形成, 都具有重要意义 (唐清山等, 1996)。

6 结论

本文提出了一个适用于高温高压 (达1000℃、1.5GPa) 多组分含盐含气混合流体 (H2O-CO2-NaCl) 的石英溶解度计算模型。在系统回顾实验数据的基础上, 笔者对前人建立的密度模型进行了改进, 并采用新的方法求取参数。相比前人模型, 本模型的计算精度更高, 适用的温度、压力、成分范围更宽广, 并且具有较好的外延性 (达到地壳温度压力范围)。本模型可广泛应用于与H2O-CO2-NaCl三元体系相关的成矿流体研究, 加深人们对于石英脉及有关矿床成因的认识, 并对石油等实际工程的开展具有指导意义。

致谢 感谢耿明博士、段先哲博士在论文成文过程中给予的意见和建议；特别感谢两位匿名审稿人提出的宝贵修改意见。
参考文献
[] Akinfiev NN, Zotov A. 1999. Thermodynamic description of equilibria in mixed fluids (H2O-non polar gas) over a wide range of temperature (25 to 700℃) and pressure (1 to 5000 bars). Geochim. Cosmochim.Acta, 63: 2025–2041. DOI:10.1016/S0016-7037(98)00304-4
[] Akinfiev NN, Diamond LW. 2009. A simple predictive model of quartz solubility in water-salt-CO2 systems at temperatures up to 1000℃ and pressures up to 1000MPa. Geochim. Cosmochim.Acta, 73: 1597–1608. DOI:10.1016/j.gca.2008.12.011
[] Anderko A, Pitzer KS. 1993. Phase equilibria and volumetric properties of the system KCl-H2O and NaCl-KCl-H2O above 573K: Equation of State representation. Geochim. Cosmochim.Acta, 57(20): 4885–4897. DOI:10.1016/0016-7037(93)90127-I
[] Anderson GM, Burnham CW. 1965. The solubility of quartz in supercritical water. American Journal of Science, 263: 494–511. DOI:10.2475/ajs.263.6.494
[] Anderson GM, Burnham CW. 1967. Reactions of quartz and corundum wity aqueous chloride and hydroxide solutions at high temperatures and pressures. American Journal of Science, 265: 12–27. DOI:10.2475/ajs.265.1.12
[] Anderson GM, Castet S, Schott J, Mesmer RE. 1991. The density model for estimation of thermodynamic parameters of reactions at high temperatures and pressures. Geochim. Cosmochim.Acta, 55: 1769–1779. DOI:10.1016/0016-7037(91)90022-W
[] Born M. 1920. Volumen und hydrationswarme der Ionen. Z. Phy., 1: 45–48. DOI:10.1007/BF01881023
[] Crerar DA, Anderson GM. 1971. Solubility and solutions reactions of quartz in dilute hydrothermal solutions. Chemical Geology, 8: 107–122. DOI:10.1016/0009-2541(71)90052-0
[] Davis MC, David JW, Jorgen Rosenqvist, Brantley SL, Mueller KT. 2011. Solubility and near-equilibrium dissolution rates of quartz in dilute NaCl solutions at 398~473K under alkaline conditions. Geochim. Cosmochim.Acta, 75(2): 401–415. DOI:10.1016/j.gca.2010.10.023
[] Fan WL, Wang SY, Tian YF. 1997. Experimental study on the complexation between silica and antimony. Acta Mineralogica Sinica, 17(4): 472–477.
[] Fournier RO. 1960. Solubility of quartz in water in the temperature interval from 25℃ to 300℃. Geol. Soc. Amer. Bull., 71: 1867-1868
[] Fournier RO. 1982. A method of calculating quartz solubilities in aqueous sodium chloride solutions. Geochim. Geochim. Cosmochim. Acta, 47: 579–586.
[] Fournier RO, Potter Ⅱ RW. 1982. An equation correlating the solubility of quartz in water from 25℃ to 900℃ at pressures up to 10, 000bars. Geochim. Cosmochim. Acta, 46: 1969–1973. DOI:10.1016/0016-7037(82)90135-1
[] Fournier RO, Rosenbauer RJ, Bischoff JL. 1982. The solubility of quartz in aqueous sodium chloride solution at 350℃ and 180 to 500 bars. Geochim. Cosmochim. Acta, 46: 1975–1978. DOI:10.1016/0016-7037(82)90136-3
[] Fournier RO. 1983. A method of calculating quartz solubilities in aqueous sodium chloride solutions. Geochim. Cosmochin. Acta, 47: 579–586. DOI:10.1016/0016-7037(83)90279-X
[] Foustoukos DI, Seyfried Jr WE. 2007. Quartz solubility in the two-phase and critical region of the NaCl-KCl-H2O system: Implications for submarine hydrothermal vent systems at 9.50'N East Pacific Rise. Geochimica et Cosmochimica Acta, 71: 186–201. DOI:10.1016/j.gca.2006.08.038
[] Franck EU. 1956. Hochverdichteter Wassedampf II. Ionendissociation von KCl in H2O bis 750℃. Z. phys. Chem., 8: 107–126. DOI:10.1524/zpch.1956.8.1_2.107
[] Franck EU. 1961. Uberkritisches Wasser als elektrolytisches Losungsmittel. Angew. Chem., 73: 309–322. DOI:10.1002/(ISSN)1521-3757
[] Ganeyev IG. 1975. Solubility and crystallization of silica in chloride. Doklady Academii Nauk SSSR, 224: 248–250.
[] Helgeson HC, Kirkham DH, Flowers GC. 1981. Theoretical prediction of the thermodynamic behavior of aqueous electrolytes at high pressures and temperatures: IV. Calculation of active coefficients, osmotic coefficients, and apparent molal and standard and relative partial molal properties to 600℃ and 5kb. Amer. J. Sci., 281: 1249–1516. DOI:10.2475/ajs.281.10.1249
[] Hemley JJ, Montoya JW, Marinenko JW, Luce RW. 1980. Equilibria in the system Al2O3-SiO2-H2O and some general implications for alteration-NOT/mineralization processes. Econ. Geol., 75: 210–228. DOI:10.2113/gsecongeo.75.2.210
[] Jasmund K. 1952. Loslichkeit von KCl in der gasphase von iiberkritische erhitzem wasser. Heidelberger Beitr. Mineral. Petrogr, 3: 380–405.
[] Johnson JW, Oelkers EH, Helgeson HC. 1992. Supcrt92: A software package for calculating the standard molal thermodynamic properties of minerals, gases, aqueous species, and reactions from 1 to 5000 bar and 0℃ to 1000℃. Comp. Geosci., 18: 899–947. DOI:10.1016/0098-3004(92)90029-Q
[] Kennedy GC. 1950. A portion of the system silica-water. Econ. Geol., 45: 629–653. DOI:10.2113/gsecongeo.45.7.629
[] Khitarov NI. 1956. The 400℃ isotherm for the system H2O-SiO2. Am. J. Sci., 260: 501–521.
[] Kitahara S. 1960. The solubility of quartz in water at high temperatures and high pressures. Rev. Phys. Chem. Jpn., 30: 109–114.
[] Manning CE. 1994. The solubility of quartz in H2O in the lower crust and upper mantle. Geochim. Cosmochim. Acta, 58: 4831–4839. DOI:10.1016/0016-7037(94)90214-3
[] Manning CE, Antignano A, Lin HA. 2010. Premelting polymerization of crustal and mantle fluids, as indicated by the solubility of albite+paragonite+quartz in H2O at 1GPa and 350~620℃. Earth and Planetary Sciences Letters, 292: 325–336. DOI:10.1016/j.epsl.2010.01.044
[] Mao SD, Duan ZH, Hu JW, Zhang DH. 2010. A model for single-phase PVTx properties of CO2-CH4-C2H6-N2-H2O-NaCl fluid mixtures from 273 to 1273K and from 1 to 5000 bar. Chemical Geology, 275(3-4): 148–160. DOI:10.1016/j.chemgeo.2010.05.004
[] Marshall WL, Mesmer RE. 1984. Pressure-density relationships and ionization equilibria in aqueous solutions. J. Soln. Chem., 13: 383–391. DOI:10.1007/BF00644070
[] Mckenzie WF, Helgeson HC. 1984. Estimation of the dielectric constant of H2O from experimental solubilities of quartz and calculation of the thermodynamic properties of aqueous species to 900℃ at 2kb. Geochim. Cosmochim. Acta, 48: 2167–2177. DOI:10.1016/0016-7037(84)90213-8
[] Mesmer RE, Marshall WL, Palmer DA, Simonson JM, Holmes HF. 1988. Thermodynamics of aqueous association and ionization reactions at high temperatures and pressures. J. Soln. Chem., 17: 699–718. DOI:10.1007/BF00647417
[] Mesmer RE, Patterson CS, Busey RH, Holmes HF. 1989. Ionization of acetic acid in NaCl (aq) media: A potentiometric study to 573K and 130bar. J. Phys. Chem., 93: 6983–6990. DOI:10.1021/j100356a021
[] Morey GW, Hesselgesser JM. 1951. The solubility of some minerals in super-heated steam at high pressures. Econ. Geol., 46: 821–835. DOI:10.2113/gsecongeo.46.8.821
[] Morey GW, Fournier RO, Rowe JJ. 1962. The solubility of quartz in water in the temperatures interval from 25℃ to 300℃. Geochim. Cosmochim. Acta, 26: 1029–1043. DOI:10.1016/0016-7037(62)90027-3
[] Mosebach R. 1957. Thermodynamic behavior of quartz and other forms of silica in pure water at elevated temperatures and pressures with conclusions on their mechanism of solution. J. Geol., 65: 347–363. DOI:10.1086/626438
[] Newton RC, Manning CE. 2000. Quartz solubility in H2O-NaCl and H2O-CO2 solutions at deep crust-upper mantle pressures and temperatures: 2~15kbar and 500~900℃. Geochim. Cosmochim. Acta, 64: 2993–3005. DOI:10.1016/S0016-7037(00)00402-6
[] Newton RC, Manning CE. 2008. Thermodynamics of SiO2-H2O fluid near the upper critical end point from quartz solubility measurements at 10kbar. Earth and Planetary Sciences Letters, 274(1-2): 241–249. DOI:10.1016/j.epsl.2008.07.028
[] Novgorodov PG. 1977. On the solubility of quartz in H2O+CO2 and H2O+NaCl at 700℃ and 1.5kbar pressure. Geochem. Int., 14(4): 191–193.
[] Quist AS. 1970. The ionization constant of water to 800℃ and 400bars. J. Phys. Chem., 74: 3393–3402.
[] Ryzhenko BN. 1981. Thermodynamics of Equilibria in Hydrothermal Solutions. Moscow: Nauka Publishers.
[] Saunders JA. 1995. Colloidal transport of gold and silica in epithermal precious-metal systems: Evidence from the Sleeper deposit, Nevada. Abroad Geology and Exploration, 3: 10–16.
[] Shmulovich K, Graham C, Yardley B. 2001. Quartz, albite and diopside solubilities in H2O-NaCl and H2O-CO2 fluids at 0.5~0.9GPa. Contrib. Mineral. Petrol., 141: 95–108. DOI:10.1007/s004100000224
[] Shmulovich KI, Yardley BWD, Graham CM. 2006. Solubility of quartz in crustal fluids: Experiments and general equations for salt solutions and H2O-CO2 mixtures at 400~800℃ and 0.1~0.9GPa. Geofluids, 6: 154–167. DOI:10.1111/gfl.2006.6.issue-2
[] Shock EL, Helgeson HC, Sverjensky DA. 1989. Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: Standard partial molal properties of imorganic neutral species. Geochim. Cosmochim. Acta, 53: 2157–2183. DOI:10.1016/0016-7037(89)90341-4
[] Siever R. 1962. Silica solubility, 0~200℃, and the diagenesis of siliceous sediments. J. Geol., 70: 127–150. DOI:10.1086/626804
[] Tang QS, Wei GP, Du DJ. 1996. Effect of quartz solubility on heavy oil reservoir. Special Oil & Gas Reservoirs, 3(Suppl.): 28–30.
[] Tanger JC Ⅳ, Helgeson HC. 1988. Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: Revised equations of state for the standard partial molol properties of ions and electrolytes. Amer. J. Sci., 288: 19–98. DOI:10.2475/ajs.288.1.19
[] Van Lier JA, de bruyn PL, Overbeek JTG. 1960. The solubility of quartz. Phys. Chem., 64: 1675–1682. DOI:10.1021/j100840a017
[] Van Nieuwenburg CJ, Van Zon PM. 1935. Semi-quantitative measurements of the solubility of quartz in super-critical steam. Recueil des Travaux Chimiques des Pays-Bas, 54(2): 129–132.
[] Von Damm KL, Bischoff JL, Rosenbauer RJ. 1991. Quartz solubility in hydrothermal seawater: An experimental study and equation describing quartz solubility for up to 0.5m NaCl solutions. American Journal of Science. American Journal of Science, 291(12): 977–1007.
[] Wagner W, Pruβ A. 2002. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. Phys. Chem. Ref. Data, 31: 387–535. DOI:10.1063/1.1461829
[] Walther JV, Helgeson HC. 1977. Calculation of the thermodynamic properties of aqueous silica and the solubility of quartz and its polymorphs at high pressures and tempetatures. Am. J. Sci., 277: 1315–1351. DOI:10.2475/ajs.277.10.1315
[] Walther JV, Orville PM. 1983. The extraction-quench technique for determination of the thermodynamic properties of solute complexes: Application to quartz solubility in fluid mixtures. Amer. Mineral., 68: 731–741.
[] Walther JV, Schott J. 1988. The dielectric constant approach to speciation and ion pairing at high temperature and pressure. Nature, 332: 635–638. DOI:10.1038/332635a0
[] Wasserburg GI. 1958. The solubility of quartz in supercritical water as a function of pressure. Geol., 66: 559–578. DOI:10.1086/626536
[] Weill DF, Fyfe WS. 1964. The solubility of quartz in H2O in the range 1000~4000bars and 400~550℃. Geochim. et Cosmochim. Acta, 28: 1243–1256. DOI:10.1016/0016-7037(64)90126-7
[] Xie ZX, Walther JV. 1992. Quartz solubilities in NaCl solutions with and without wolllastonite at elevated temperatures and pressures. Geochimica et Cosmochimica Acta, 57: 1947–1955.
[] Zhang S, Li TJ. 1997. Solubility equations and geothermometers of silica: An overview. Geological Science and Technology Information, 16(1): 53–58.
[] 樊文苓, 王声远, 田弋夫. 1997. SiO2与成矿元素Sb络合作用的实验研究. 矿物学报, 17(4): 472–477.
[] Saunders JA. 1995. 胶体证据和低温热液成矿标志--美国内华达州洪堡郡Sleeper矿床富矿体中的硅-金结构. 国外地质与勘测, 3: 10–16.
[] 唐清山, 魏桂萍, 杜德军. 1996. 石英溶解对稠油储层的影响. 特种油气藏, 3(增刊): 28–30.
[] 张生, 李统锦. 1997. 二氧化硅溶解度方程和地温计. 地质科技情报, 16(1): 53–58.