文章信息
- 张宏帅, 朱高龙, 吴家煜, 吴锡麟
- ZHANG Hongshuai, ZHU Gaolong, WU Jiayu, WU Xilin
- 基于BP神经网络与Kriging结合的土壤有机质空间分布模拟——以福建省华安县为例
- Simulation of spatial distribution simulation of soil organic matter based on BP neural network and Kriging interpolation—Taking Hua'an County, Fujian Province as an example
- 亚热带农业研究, 2021, 17(1): 40-47
- Subtropical Agriculture Research, 2021, 17(1): 40-47.
- DOI: 10.13321/j.cnki.subtrop.agric.res.2021.01.008
-
文章历史
- 收稿日期: 2021-02-02
2. 闽江学院海洋学院, 福建 福州 350108
2. College of Oceanography, Minjiang University, Fuzhou, Fujian 350108, China
耕地土壤有机质是农作物生长的重要物质基础之一。土壤有机质含量是监测土壤肥力的重要指标之一,很大程度上决定了农田的肥力状态[1-2]。快速精准地掌握耕地土壤有机质的空间分布,对于提高农田的水肥利用效率与改善田间管理,推进“精准农业”具有重要意义[3]。土壤有机质的涵养、运移、分布是复杂的物理、化学和生物过程,受气候、地貌、地下水、微生物以及土壤类型、土地利用方式等多种地表环境因素的共同作用[4-7], 这些因素可以分为定量因素(如海拔高度、坡度、地理坐标等)和定性因素(如土壤类型、土地利用等)两种类型。
引入外界辅助变量可在一定程度上提高土壤有机质空间分布的预测精度[8]。在引入外界辅助信息进行土壤有机质空间分布的预测方法中,回归克里金法(regression Kriging, RK)应用较为广泛[9-10]。RK法主要利用多元线性回归得到辅助信息与目标变量的回归方程,能够给出最优线性无偏估计,但难以模拟土壤有机质含量的影响因素之间的非线性和复杂性。近年来随着神经网络算法的迅速发展,尤其是BP神经网络,具有强大的非线性运算能力为预测土壤有机质含量提供了新方法[11]。江叶枫等[12]以地理坐标、高程和坡度及邻近样点信息作为网络的输入变量,研究表明集成BP神经网络模型预测效果最好。刘二永等[13]结合外界环境因子,利用回归—光滑薄板样条插值法得到了较好的预测结果。George et al[14]研究发现,利用可见—近红外高光谱反射率构建人工神经网络模型可快速准确地预测有机质的空间分布。目前大多数预测模型仅仅引入定量因素,忽略了定性因素对有机质空间分布的影响,在一定程度上影响预测结果的精度[15]。
本文以漳州市华安县为例,利用与县域尺度土壤有机质含量紧密相关的土壤类型、土壤质地、土地利用、海拔高度、地形坡度等数据,采用BP神经网络与克里金插值相结合的方法(BP_OK)进行耕地土壤有机质空间分布模拟,并与回归克里金插值法(RK)、普通克里金插值法(ordinary Kriging, OK)对比,探索县域尺度上快速准确获取土壤有机质空间分布的新方法。
1 材料与方法 1.1 研究区概况华安县位于福建省漳州市西北部,九龙江北溪中游,地理坐标为117°15′~117°42′E、24°38′~24°15′N。华安县地貌以山地、丘陵为主,占全县总面积的95.5%,台地平原仅分布在南部,占4.5%。根据2018年度华安县土地利用现状图(http://www.dsac.cn/)统计,华安县土地总面积127 760.49 hm2,其中耕地面积16 166.13 hm2,占土地总面积的12.65%。耕地以水田为主,面积15 129.60 hm2,占耕地总面积的93.59%;旱地1 035.33 hm2,占耕地总面积的6.40%;水浇地1.20 hm2,占耕地总面积的0.01%。受地形影响,耕地类型主要包括山垄田、洋面田、梯田、溪边田等。根据第2次土壤普查结果( http://vdb3.soil.csdb.cn/),华安县耕地土壤类型可分为红壤、水稻土、赤红壤和黄壤,其中红壤面积(约7 518 hm2)最大,水稻土面积(约5 774 hm2)其次,赤红壤约2 668 hm2,黄壤约206 hm2,分别约占耕地总面积的46.51%、35.72%、16.50%、1.27%。
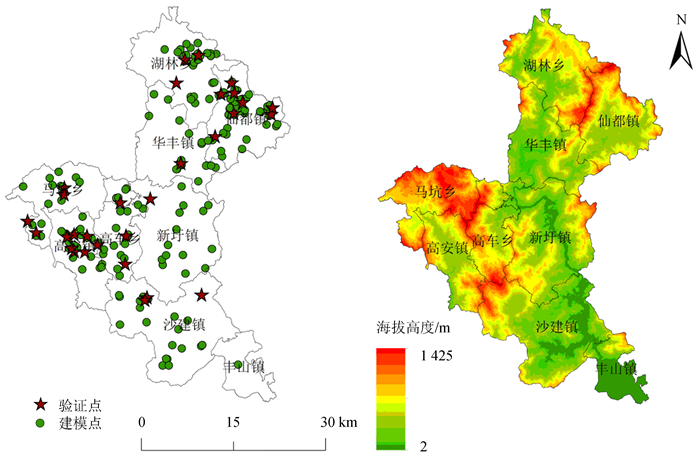
1.2 数据来源及处理 1.2.1 土壤有机质数据样地土壤有机质含量数据来源于2014—2018年华安县耕地质量等别年度更新评价中的实地采样数据。所有样地采样均在每年秋收后进行,在边长为10 m的正方形样地内采用梅花形采样法布设5个样点,每个样点使用土钻获取表层0~20 cm深度的土样。每个样地的土样经充分混合后,利用四分法取1 kg混合土样送往实验室,利用重铬酸钾外加热法[16]测定该样地的土壤有机质含量。全县共采集215个有效样点,其中185个用于空间插值建模,30个用于模型精度验证(图 1)。全县土壤样点有机质含量最小值为10.00 g·kg-1,最大值为36.92 g·kg-1,平均含量为21.07 g·kg-1,变异系数为30.85%,属于中等性变异,说明华安县耕地土壤有机质存在中等程度的空间变异性。
|
图 1 华安县耕地土壤有机质样地及海拔高度分布图 Figure 1 Distribution map of cultivated soil organic matter plot and altitude in Hua′an County |
土地利用类型采用了2018年度华安县土地利用现状图中水田、旱地、水浇地3种二级地类。海拔高度采用从地理空间数据云(http://www.gscloud.cn/)下载的30 m空间分辨率的ASTER GDEM数据,坡度由ASTER GDEM数据在ArcGIS 10.2中生成导出。土壤类型、土壤质地数据来自于全国第2次土壤普查,其中土壤质地数据为砂土、粉砂土与黏土所占的百分比。上述影响因素的图层均重采样为30 m空间分辨率的栅格数据,用于土壤有机质空间插值分析。
1.3 研究方法 1.3.1 虚拟变量的引入土壤类型、土地利用、土壤质地等因素在很大程度上影响着土壤有机质的空间分布,因此在预测过程中应综合考虑这些因素所带来的影响。与海拔高度、坡度等连续型变量不同的是,土壤类型、土地利用为定性变量中的分类变量,其数值只代表不同分类,需要将其转换为虚拟变量代入回归分析[17]。将虚拟变量引入回归模型,虽然使模型变得较为复杂,但可以更直观地反映出该自变量的不同属性对因变量的影响,提高了模型的精度和准确度。
虚拟变量取值通常为0、1,其数值用来反映某个变量的不同属性,不代表实际大小[18]。在回归分析中,定义虚拟变量时为了避免共线性,当回归模型包含截距时,如果变量具有n个分类,需定义n-1个虚拟变量来表示这些类别[19]。其赋值方法有多种,本研究选取的赋值方法为:
| $ {X_i} = \left\{ \begin{array}{l} 1\;\;\;\;第i类\;\;\;\;\;\;\;\;\;(i = 1, 2, \cdots \cdots n - 1)\\ 0\;\;\;\;其他 \end{array} \right.\; $ | (1) |
式(1)中,Xi为分类变量,i表示分类变量下的不同属性,通常需选取分类变量中的某一属性作为参考类型,且该属性应有一定的样本量。本研究中将土壤类型和土地利用转换为虚拟变量。土壤类型选取水稻土、红壤、赤红壤三类,以水稻土为参考类型;耕地利用类型选取水田和旱地两类,以旱地为参考类型。
1.3.2 OK插值OK插值是基于变异函数模型在有限区域内对区域化变量的取值进行无偏最优估计的空间插值方法,是地统计学的主要内容之一[20]。该方法克服了经典统计学将地学变量看成纯随机变量而忽略其空间相关性的不足,降低了估计误差。经检验,本研究样本数据近似符合正态分布,满足地统计学的基本要求,再利用地统计模块选择最佳半变异函数模型参数,在ArcGIS 10.2中完成OK插值过程。
1.3.3 RK插值RK插值首先通过分析外界环境变量与目标变量之间的关系,然后利用多元逐步回归分析得到一个线性回归方程;再通过该方程得到关于确定性部分的趋势项以及代表随机部分的残差项,将残差项作为一个新的随机变量进行克里金插值,最后将趋势项和残差项进行叠加,即得到该区域的土壤有机质的空间分布模拟图。其过程可表示为:
| $ f(x) = m(x) - \varepsilon (x) $ | (2) |
式(2)中,f(x)为RK插值在点x处的土壤有机质预测值; m(x)为在x处经多元逐步回归得到的趋势项; ε(x)为克里金插值在x处的残差项。
在回归分析输入虚拟变量的过程中,为确保所有虚拟变量具有正确的含义,需要使用强制进入法以保证所有虚拟变量都能留在最后的模型中。其回归过程如表 1所示。由于砂土、粉砂土和黏土为百分比数据,其总和为1,三者存在共线性,因此在回归过程中剔除黏土数据。最大方差膨胀系数(variance inflation factor, VIF)为4.021,小于10,说明变量之间不存在共线性。标准化前系数是拟合方程的实际参数,而标准化后参数的大小说明了自变量对因变量的重要程度[21]。在α=0.05的检验水准下,土地利用和土壤类型虚拟变量的回归系数检验P值均小于0.05,说明不同分类下土壤有机质含量(SOM)存在显著差异。最终选取的回归模型为:
| $ {\rm{SOM = 40}}{\rm{.163 + 5}}{\rm{.432}}{x_{\rm{1}}} - 34.714{x_2} - 30.235{x_3} + 0.008{x_4} - 0.143{x_5} - 2.392{x_6} - 5.154{x_7} $ | (3) |
| 模型变量 | 非标准化系数 | 标准系数 | t | Sig | 共线性统计量 | ||
| 回归系数 | 标准误差 | 容差 | VIF | ||||
| 常量 | 40.163 | 10.866 | 3.696 | 0.000 | |||
| x1 | 5.432 | 0.890 | 0.409 | 6.107 | 0.000 | 0.881 | 1.135 |
| x2 | -34.714 | 22.051 | -0.198 | -1.574 | 0.117 | 0.249 | 4.021 |
| x3 | -30.235 | 12.252 | -0.270 | -2.468 | 0.015 | 0.331 | 3.021 |
| x4 | 0.008 | 0.002 | 0.270 | 3.342 | 0.001 | 0.604 | 1.656 |
| x5 | -0.143 | 0.067 | -0.151 | -2.134 | 0.034 | 0.790 | 1.266 |
| x6 | -2.392 | 1.096 | -0.183 | -2.182 | 0.030 | 0.559 | 1.787 |
| x7 | -5.154 | 2.185 | -0.217 | -2.359 | 0.019 | 0.465 | 2.152 |
| 1)x1为水田, x2为砂土, x3为粉砂土, x4为海拔高度, x5为坡度, x6为红壤, x7为赤红壤; VIF为方差膨胀系数。 | |||||||
式(3)中,SOM为土壤有机质含量(g·kg-1);x1为水田, x2为砂土, x3为粉砂土, x4为海拔高度, x5为坡度, x6为红壤, x7为赤红壤。
1.3.4 BP_OK插值BP_OK插值模型是将BP神经网络与克里金插值相结合的一种方法,其原理与RK插值相似,但其中趋势项为BP神经网络计算的预测结果。BP神经网络是一种多层前馈神经网络,采用后向传播学习算法,是目前应用最多也是最成功的神经网络之一[22-23]。其模型由输入层、隐含层和输出层组成,相邻层的神经元之间基于权重系数进行相互连接,同一层内部的神经元是平行的、相互之间没有连接关系[24]。根据实际需要可选择单层神经网络和多层神经网络。在神经网络预测中,首先读取训练数据和测试数据,利用Python编程实现BP神经网络训练。训练方式选择梯度下降方法,激活函数为Relu函数,通过调节隐含层个数及节点数、学习率、迭代次数等参数,确定最优模型。由试验可知,当迭代次数在500左右时,其损失函数趋于稳定。采用双隐含层结构(第1个隐含层为11个节点,第2个隐含层为5个节点),学习率为0.01时预测模型最好。再将整个研究区的栅格数据输入到训练好的模型中,最终以图像格式输出研究区的土壤有机质含量分布图。
1.3.5 精度评价为验证实验结果的预测精度,随机选取30个土壤有机质样点作为验证样本,以均方根误差(RMSE)、平均绝对误差(MAE)及相关系数(R)作为精度评价标准。
| $ {\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^n {{{({{\overline X }_i} - {X_i})}^2}} } $ | (4) |
| $ {\rm{MAE}} = \frac{1}{n}\sum\nolimits_{i = 1}^n {|{{\overline X }_i} - {X_i}|} $ | (5) |
| $ R = \frac{{{\rm{Cov}}({{\overline X }_i},{X_i})}}{{\sqrt {{\rm{Var}}[{{\bar X}_i}]{\rm{Var}}[{X_i}]} }} $ | (6) |
式(4)~(6)中,n为样本个数,Xi为预测值,Xi为实测值,Cov(Xi, Xi)为Xi和Xi的协方差,Var[Xi]为Xi的方差,Var[Xi]为Xi的方差。当RMSE和MAE越小、R越大时,预测效果则越好。
2 结果与分析 2.1 土壤有机质空间插值模型表 2列出了3种插值方法最佳模型的块金值、基台值、块基比和变程。OK、RK法最佳理论模型为指数模型,BP_OK法最佳理论模型为高斯模型。3种方法的块基比均在25%~75%之间,表现为中等强度的空间依赖性[25],说明该研究区土壤有机质空间分布受自然因素和人为因素的双重影响。OK插值变程为528 m,相对较小,说明其空间自相关性较小,这与华安县复杂地形地貌空间结构特征相符合;RK、BP_OK插值变程相对较大,分别为3 560、2 524 m,说明结合辅助因素后削弱了外界因素的影响,插值点的空间自相关范围变大。将残差插值结果与趋势面进行栅格运算叠加, 并由土地利用矢量图斑裁剪可得出该区域的耕地土壤有机质含量空间分布。
| 方法 | 最佳 模型 |
块金值 | 基台值 | 块基比 | 变程 | |
| % | m | |||||
| OK | 指数 | 18.56 | 28.87 | 64.29 | 528 | |
| RK | 指数 | 16.99 | 43.18 | 39.35 | 3 560 | |
| BP_OK | 高斯 | 21.94 | 44.19 | 49.65 | 2 524 |
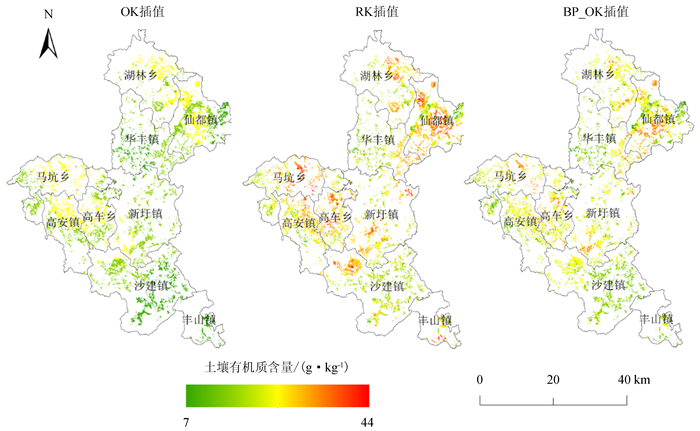
由图 2可知,3种插值方法得出的土壤有机质含量空间分布规律基本一致,总体上呈现北部和西部较高、南部及中部偏低的空间格局。这与地貌类型空间分布特征基本吻合,其中高值区主要分布在仙都镇、高车乡、湖林乡东部及马坑乡东部,低值区主要分布在华丰镇、沙建镇、丰山镇。3种插值方法得到的低值区分布面积依次为:OK>RK>BP_OK,高值区分布面积依次为:RK>BP_OK>OK。但是,不论高值区或低值区,OK插值结果都明显小于RK法和BP_OK法。从视觉效果上看,OK插值呈块状分布,不同区域(高值区、低值区)之间分级明显,低值区主要出现在海拔较低的平原区,高值区主要分布在海拔较高的山地、丘陵区,这与华安县海拔高度变化情况相吻合。由于OK法仅考虑有限样点的空间相关性,无法拟合局部变异现象,只能反映研究区土壤有机质空间变异的总体趋势。RK法和BP_OK法插值结果局部空间变化相对显著,均在一定程度上缓和了OK插值块状图斑现象,这是因为BP_RK法与RK法采取逐个像元计算的方法,充分利用了自然因素及人为因素对土壤有机质含量空间分布影响的先验知识,弥补了样点数据有限的问题,能够反映因局地因素变化而导致的土壤有机质含量的空间分异现象。
|
图 2 不同插值方法的华安县耕地土壤有机质空间分布图 Figure 2 Spatial distribution map of cultivated soil organic matter by different interpolation methods |
3种插值方法中,OK插值的有机质含量值域范围最小,最小值为13.94 g·kg-1,最大值为28.41 g·kg-1,主要集中在15~25 g·kg-1之间,平均值最小(20.88 g·kg-1)。RK插值的有机质含量最小值、最大值、平均值分别为7.00、43.80、23.35 g·kg-1,其值域范围和平均值在3种插值方法中都最大。BP_RK插值结果位于OK法和RK法之间,有机质含量最小值、最大值、平均值分别为9.94、32.69、22.71 g·kg-1。从地貌上看,山地区平均有机质含量最高、丘陵区次之、平原区最低,表现为土壤有机质含量与海拔高度呈正相关,这与前人研究成果相一致[26-27],主要是因为高海拔地区有利于土壤有机质的积累。从土地利用上看,水田的有机质含量明显高于旱地,说明耕作方式导致土壤有机质含量在空间分布上存在差异。从土壤类型上看,水稻土有机质含量最高、红壤次之、赤红壤最低, 这与建模样点具有同样的空间分布特征。
2.3 精度分析利用30个土壤有机质样点验证不同插值方法的预测精度(表 3)。从表 3可见,3种插值方法的RMSE分别为3.55、3.73、4.92 g·kg-1,以BP_OK法最小,表明预测值离散程度最小;MAE分别为2.96、3.06、4.02 g·kg-1,以BP_OK法最小,说明整体上其预测值与实测值最为接近;R分别为0.72、0.68、0.35,表明BP_OK法和RK法预测值与实测值呈高度相关,OK法表现为中等相关。综上可知,结合土壤类型、土壤质地、土地利用、海拔高度和地形坡度等辅助信息的BP_OK法、RK法插值精度明显优于仅考虑样点空间自相关性的OK插值法。与RK插值结果相比,BP_OK插值结果的预测值和实测值相关系数更高,预测值RMSE、MAE更小。以上表明,BP_OK法整体拟合效果最优,这是因为BP神经网络具有高度非线性和较强的泛化能力,能以任意精度逼近任意连续函数,能够更好地拟合输入数据与土壤有机质含量的影响因素的非线性关系,具有较好的预测能力。BP_OK法可以有效提高县域尺度下耕地土壤有机质空间分布模拟精度。
| 方法 | RMSE | MAE | R | ||
| g·kg-1 | g·kg-1 | ||||
| OK | 4.92 | 4.02 | 0.35 | ||
| RK | 3.73 | 3.06 | 0.68 | ||
| BP_OK | 3.55 | 2.96 | 0.72 |
OK法是土壤有机质空间分布模型中最常用的方法,能够从变量自身出发,充分考虑有机质的空间变异,利用邻近采样点之间的相关性来预测未知点,并且能够统计预测结果的误差,因此在土壤属性的空间预测中得到广泛应用。姜赛平等[28]认为,OK插值结果不够精细,图斑较大,不能刻画土壤有机质含量的细部特征,仅能预测有机质含量整体空间分布,通常适用于土壤属性变化较为均匀的区域,这与本研究结果相一致。
在地貌特征复杂的地区,土壤有机质的空间分布更受限于外界人为因素和自然因素的影响,仅仅依靠采样点的空间自相关性往往不能准确模拟土壤有机质的空间分布。因此,很多学者尝试利用结合外界辅助信息的空间插值方法如回归模型、地理加权回归模型、神经网络模型等, 预测土壤有机质的空间分布,均在不同程度上提高了有机质的空间预测精度。回归模型不仅能够筛选出对有机质含量有显著性影响的环境因子而建立模型,还能利用残差信息进行普通克里金插值,考虑了对结构性和随机性的空间模拟[29],地理加权回归模型克服了回归模型中不同空间位置的环境因子权重一致的不足,提高了插值精度[30];神经网络模型能够刻画外界因素与土壤有机质含量之间的非线性关系,更加切合实际[31]。
多数学者通常选取海拔高度、坡度、地理坐标、邻近信息等定量因素作为预测模型的输入信息,而忽略了土地利用、土壤类型等定性因素对土壤有机质的影响,而在地貌特征复杂的南方地区,土壤有机质含量很大程度上取决于土地利用类型和土壤类型。本文将土壤类型、土地利用等定性因素转化为虚拟变量,再结合土壤质地、海拔高度、坡度等定量因素引入RK和BP_OK插值模型,其插值精度明显优于仅依靠有限采样点之间空间相关性的OK插值法,证明了该方法引入的各种定量和定性先验知识,可有效提高土壤有机质含量空间插值精度,且可弥补样点信息量不足,反映局地范围土壤有机质含量的空间分异变化。
从模型的精度及性能上看,BP_OK插值精度较高,但存在需要反复训练、不断调节参数才能使模型收敛的问题,而RK插值训练过程简练、计算量少,相关因素与土壤有机质含量之间的关系可用公式具体表示,能够直观地看出每种因素对土壤有机质含量的影响,但模型过于简单,在一定程度上不能准确地描述外界因素与土壤有机质之间的真实关系。
受限于县域尺度耕地土壤有机质含量影响因素的可获取性以及空间分辨率的要求,本文仅考虑了与土壤有机质含量密切相关的土壤类型、土壤质地、土地利用、海拔高度、地形坡度等5种因素。实际上,耕地土壤有机质含量影响因素复杂多样,除了土壤类型、质地、微生物、pH值等土壤本身各种属性外,还包括影响土壤发育的各种自然环境因素如气候、母质、地貌、植被和地下水等,以及强烈的人为干扰,如施肥、灌溉、耕作制度和利用方式等。引入更多更全面的外部辅助信息,有助于提高土壤有机质含量空间插值精度,但是引入影响因素较多,各因素之间可能存在相关性,则需要消除冗余数据、降低模型复杂度,进一步提升模型预测能力。
4 结论本文以华安县为研究区,结合外界定性、定量因素,构建了基于非线性拟合的BP_OK插值法,并以OK法、基于线性拟合的RK插值法为参照,对华安县耕地土壤有机质进行空间分布模拟。插值结果显示,华安县耕地土壤有机质在整体上呈现北部和西部较高,南部及中部偏低的空间分布特征,这与地貌特征、土地利用类型和土壤类型密切相关。验证结果显示,构建结合外界因素插值模型的BP_OK法和RK法其插值精度较OK法有明显提高,说明外界因素对有机质的空间分布有重要影响;BP_OK插值结果的RMSE、MAE及R等精度指标均优于RK插值结果,说明了BP神经网络与克里金插值相结合的非线性拟合法优于多元线性回归克里金插值法,这是因为线性模型难以模拟土壤影响因子之间复杂的非线性关系,BP神经网络具有非线性映射能力,可以进一步提高县域尺度下耕地土壤有机质空间分布模拟精度。
| [1] | 李启权, 王昌全, 岳天祥, 等. 基于RBF神经网络的土壤有机质空间变异研究方法[J]. 农业工程学报, 2010, 26(1): 87–93. DOI: 10.3969/j.issn.1002-6819.2010.01.015 |
| [2] | 杨奇勇, 杨劲松, 姚荣江, 等. 耕地土壤有机质空间变异性的随机模拟[J]. 农业工程学报, 2010, 26(12): 324–329. DOI: 10.3969/j.issn.1002-6819.2010.12.055 |
| [3] | 李启权. 基于RBF神经网络的土壤属性信息空间插值方法研究[D]. 雅安: 四川农业大学, 2006. |
| [4] | MOHAMED E S, ABU-HASHIM M, ABDELRAHMAN M A, et al. Evaluating the effects of human activity over the last decades on the soil organic carbon pool using satellite imagery and GIS techniques in the Nile Delta area, Egypt[J]. Sustainability, 2019, 11(9): 2644. DOI: 10.3390/su11092644 |
| [5] | 鲍丽然, 周皎, 李瑜, 等. 渝西北土壤有机质空间变异及影响因素分析[J]. 西南农业学报, 2017, 30(11): 2541–2547. |
| [6] | 刘永红, 倪中应, 谢国雄, 等. 浙西北丘陵区农田土壤微量元素空间变异特征及影响因子[J]. 植物营养与肥料学报, 2016, 22(6): 1710–1718. |
| [7] | FUSARO C, SARRIA-GUZMÁN Y, CHÁVEZ-ROMERO Y A, et al. Land use is the main driver of soil organic carbon spatial distribution in a high mountain ecosystem[J]. Peer J, 2019, 7(5): e7897. |
| [8] | 江叶枫, 郭熙, 叶英聪, 等. 基于辅助变量和神经网络模型的土壤有机质空间分布模拟[J]. 长江流域资源与环境, 2017, 26(8): 1150–1158. |
| [9] | 聂哲, 李秀芬, 吕家欣, 等. 东北典型黑土区表层土壤有机质含量高光谱反演研究[J]. 土壤通报, 2019, 50(6): 1285–1293. |
| [10] | 陈琳, 任春颖, 王宗明, 等. 基于克里金插值的耕地表层土壤有机质空间预测[J]. 干旱区研究, 2017, 34(4): 798–805. |
| [11] | 姚聪. 基于卷积神经网络的耕层土壤有机质含量估测模型研究[D]. 泰安: 山东农业大学, 2020. |
| [12] | 江叶枫, 郭熙, 叶英聪, 等. 应用集成BP神经网络模型预测土壤有机质空间分布[J]. 江苏农业学报, 2017, 33(5): 1044–1050. DOI: 10.3969/j.issn.1000-4440.2017.05.013 |
| [13] | 刘二永, 刘健, 余坤勇, 等. 基于环境因子和R-STPS的林地土壤有机质预测模型[J]. 农业机械学报, 2015, 46(1): 133–137. |
| [14] | GEORGE J, KUMAR S, ARYA RAJ R. Soil organic carbon prediction using visible-near infrared reflectance spectroscopy employing artificial neural network modelling[J]. Current Science, 2020, 119(2): 377–381. |
| [15] | 任丽, 杨联安, 王辉, 等. 基于随机森林的苹果区土壤有机质空间预测[J]. 干旱区资源与环境, 2018, 32(8): 141–146. |
| [16] | 吴鹏飞. 川东平行岭谷区土壤有机质时空变异特征研究: 以达县为例[D]. 重庆: 西南大学, 2011. |
| [17] | 李可, 杨勇, 刘亚军, 等. 基于回归克里格的河北省土壤有机质时空变化特征研究[J]. 中国土壤与肥料, 2020(3): 1–7. |
| [18] | 田海涛. 带有序多分类解释变量的线性回归模型估计方法及其应用研究[D]. 成都: 西南交通大学, 2019. |
| [19] | 戴金辉. 虚拟变量回归及其应用[J]. 统计与决策, 2019, 35(5): 77–80. |
| [20] | 王政权. 地统计学及在生态学中的应用[M]. 北京: 科学出版社, 1999: 74-96. |
| [21] | 宋娜. 多元Logistic分布及其参数估计[D]. 北京: 北京工业大学, 2007. |
| [22] | 叶勤, 姜雪芹, 李西灿, 等. 基于高光谱数据的土壤有机质含量反演模型比较[J]. 农业机械学报, 2017, 48(3): 164–172. |
| [23] | AGHAJANI M, JALALIAN A, BESALATPOUR A A. Soil particulate organic matter (POM) prediction in a mountainous watershed using artificial neural networks[J]. Communications in Soil Science and Plant Analysis, 2015, 46(8): 925–938. DOI: 10.1080/00103624.2015.1018519 |
| [24] | 张森, 卢霞, 聂格格, 等. SVM和BP检测滨海湿地土壤有机质[J]. 光谱学与光谱分析, 2020, 40(2): 556–561. |
| [25] | CAMBARDELLA C A, MOORMAN T B, NOVAK J M, et al. Field-scale variability of soil properties in central Iowa soils[J]. Soil Science Society of America Journal, 1994, 58(5): 1501–1511. DOI: 10.2136/sssaj1994.03615995005800050033x |
| [26] | 陈桂香, 高灯州, 曾从盛, 等. 福州市农田土壤养分空间变异特征[J]. 地球信息科学学报, 2017, 19(2): 216–224. |
| [27] | 余笑眉, 吕晓男, 王美琴, 等. 南方丘陵耕地土壤有机质空间插值精度比较: 以衢江区为例[J]. 浙江农业学报, 2010, 22(5): 639–643. DOI: 10.3969/j.issn.1004-1524.2010.05.019 |
| [28] | 姜赛平, 张怀志, 张认连, 等. 基于三种空间预测模型的海南岛土壤有机质空间分布研究[J]. 土壤学报, 2018, 55(4): 1007–1017. |
| [29] | PICCINI C, MARCHETTI A, FRANCAVIGLIA R. Estimation of soil organic matter by geostatistical methods: use of auxiliary information in agricultural and environmental assessment[J]. Ecological Indicators, 2014, 36: 301–314. DOI: 10.1016/j.ecolind.2013.08.009 |
| [30] | 杨顺华, 张海涛, 郭龙, 等. 基于回归和地理加权回归Kriging的土壤有机质空间插值[J]. 应用生态学报, 2015, 26(6): 1649–1656. |
| [31] | 尹群, 郭纪敏, 张世文, 等. 基于辅助变量的县域土壤有机质预测[J]. 江苏农业科学, 2020, 48(24): 267–273. |
 2021,Vol. 17
2021,Vol. 17


