收稿日期: 2016-03-08
叶面积指数LAI(Leaf Area Index)是描述植被冠层几何结构的基本参数之一,被定义为单位地表面积上所有叶片面积的一半(Chen和Black,1992),它控制着植被的许多生物物理过程,如光合作用、呼吸作用、蒸腾作用、碳循环和降水截获(胡少英和张万昌,2005)等,是陆面过程一个十分重要的结构参数(方秀琴 等,2004)。遥感具有更新周期短、监测面积大的优势,是生产区域与全球LAI产品的主要手段。近年来,基于AVHRR、VEGETATION、MODIS、MISR等传感器生产了多个全球LAI产品(Morisette 等,2006),这些产品在科学研究和生产实践中得到了广泛应用。然而,无论是从产品使用者还是算法研究者的角度来看,都需要了解LAI产品的数据质量以及反演算法在不同地表类型下的适用性,这些信息需要通过对遥感产品进行真实性检验来获得(Yang 等,2006)。
LAI产品真实性检验工作的结果不仅仅是得到待检验产品与参考产品的偏差,还应该进一步分析造成两者之间偏差的来源因素。以MODIS LAI产品为例,目前已有很多对MODIS LAI产品进行真实性检验的工作(Wang 等,2004;胡少英和张万昌,2005;Pandya 等,2006)Serbin 等,2013;Jin 等,2014;Li 等,2014),这些研究提供了MODIS LAI产品真实性检验的结果,得出MODIS LAI产品存在高估或者低估的现象,并定量给出了产品的不确定性,然而并没有对影响MODIS LAI产品真实性检验结果的因素进行分析。Chen等人(2002),Tian等人(2002),杨飞等人(2010),朱小华等人(2010)在MODIS LAI产品真实性检验基础上,分析认为MODIS LAI产品的不确定性主要来源于地表的空间异质性。Yang等人(2006)指出影响MODIS LAI产品质量的因素主要有以下3个方面,一是地表分类数据的不确定性,二是地表反射率数据的不确定性,三是用于构建查找表的MODIS算法的不确定性。吴小丹等人(2014)从地面测量、模型以及聚集效应3个方面分析真实性检验过程的不确定性,并针对问题提出了减小不确定性的办法。以上研究从真实性检验到不确定性因素的描述以及提出如何减小不确定性的建议,对遥感产品的真实性检验工作具有一定的借鉴意义。但是,在他们的工作中对不确定性因素仍然处在定性描述的阶段,未能定量化表达各个因素对真实性检验结果的影响。孙晨曦等人(2014)将遥感产品真实性检验误差分解为模型误差,数据定量化误差和尺度效应3个方面,利用数据之间的简单对比定量分析了各个误差因素对结果的影响,发现模型对结果的影响最大,使得MODIS LAI产品高估约44.2%。
本文利用时间序列的地面实测数据和高分辨率遥感数据,基于NDVI-LAI半经验模型得到参考数据,对MODIS LAI产品进行真实性检验。在此基础上进一步将偏差来源分解为反演模型、反射率数据以及聚集效应(Ryu 等,2010)3个方面,并建立偏差分析流程,定量分析各个因素对真实性检验结果的影响。
2、 材料和方法 (2.1) 研究区与地面实测数据研究区位于河北省张家口市东花园镇的中国科学院遥感试验站(40°20′57″N,115°47′3″E),研究区地理位置及样方分布如图1所示,该区域地表覆盖类型简单,除北部的水库外,其余均为玉米种植区,选择包含该研究区的3 km×3 km的范围作为真实性检验区域。该区域内,玉米在DOY=217之前,处于生长期,在DOY=217—233处于稳定期,在DOY=233之后处于衰减期。2013年7月4号(DOY=185)到2013年8月28号(DOY=240)采用由北京师范大学设计并实现的一种LAI自动测量系统—LAINet进行了实地LAI数据的获取。对于LAINet的详细介绍请参考已有的研究成果(屈永华 等,2012;Qu 等,2014a,2014b,2014c)。在2 km×2 km范围内布设了15个样方,样方大小为30 m×30 m,并在每个样方中均匀部署了4个LAINet节点进行逐日观测。在后期数据处理时,将每日LAI数据进行8天平均,得到与MODIS LAI产品时间相对应的地面实测数据集。
在LAINet观测的同时,在试验站旁边(40°20′59″N,115°47′7″E)布设了一个样方(30×30 m),在样方内选择两块能够代表该样方玉米长势的标准样地(2 m×2 m),在每个样地内布设4个LAINet节点。在每个标准样地外面,通过目视选取与标准样地中玉米长势相近的样方进行破坏性测量,得到LAI真实值。破坏性LAI值测量方法是,在样方内随机选取2个植株的玉米叶子,利用LI-3000叶面积仪测量叶片面积,然后根据样方面积以及标准样地内的植株数量关系,推算到整个样方内,从而计算得到样方的LI-3000观测结果。以上地面测量数据来自《河北怀来试验站LAINet观测数据集》(屈永华,2013)。

|
| 图 1 采样点分布图(背景是2013年8月23日Landsat 8 OLI标准假彩色合成图像) Figure 1 Sampling points in experiment area where the background image is Landsat 8 OLI false-color composite image using bands 5, 4, 3 at the date of August 23, 2013 |
相对于待检验的MODIS LAI产品而言,将高分辨率遥感数据称之为过渡尺度遥感数据。本研究所用的过渡尺度遥感数据是Landsat 8 OLI数据,其多光谱波段的空间分辨率为30 m,与研究区的样方大小一致。根据研究区的地理位置和实测LAI数据获取时间,同时又考虑云的影响,在中国科学院网络信息中心国际科学数据镜像网站([2016-03-08])下载了3景Landsat 8 OLI数据。数据的基本信息见如表1所示。
|
|
表 1 Landsat 8 OLI数据 Table 1 Landsat 8 OLI data |
该数据的投影为UTM-WGS84,是L1T级的标准地形校正数据,经过了系统辐射校正、几何校正和地形校正,具有较高的地理精度。结合Landsat 8 OLI传感器辐射定标参数,将遥感影像的DN值数据转换为大气顶层观测的辐亮度数据,并利用MODIS同步观测的大气参数,结合6S辐射传输模型,对辐亮度图像进行逐像元的大气辐射校正处理,得到地表的真实反射率数据(刘良云,2014)。
2.2.2. MODIS LAI产品待检验的卫星产品为第五版本的MOD15A2 LAI,该产品是8 d合成数据,空间分辨率为1000 m。MODIS产品为Sinusoidal投影,为了与Landsat 8 OLI数据投影一致,利用MRT(MODIS Reprojection Tool, [2016-03-08])将MODIS LAI产品转换为UTM-WGS84投影。并根据研究区的范围,对MODIS LAI产品进行裁剪。本研究所使用的MODIS LAI产品数据来自于[2016-03-08]。具体信息如表2所示。
|
|
表 2 待检验的MODIS LAI产品 Table 2 Information of MODIS LAI product |
综上所述,为了开展MODIS LAI产品的真实性检验工作,一共用到了4种数据,时相上保持一致或者临近,具体信息如表3所示。
|
|
表 3 数据列表 Table 3 Data list |
用植被指数与LAI的统计分析模型来估算LAI是一种简洁、有效的估算方法。归一化植被指数(NDVI)与LAI之间存在很大的相关性,因此,常用于LAI估算(Baret和Guyot,1991)。本研究选择了半经验的LAI统计模型将地面点数据扩展至过渡尺度。半经验的统计模型为
| ${\rm{NDVI}} = A - B \times \exp \left( { - C \times {\rm{LAI}}} \right)$ | (1) |
式中,A、B和C均为经验系数,具体值与实验站点与作物类型有关系。
在对A、B、C参数拟合时,随机选择70%的数据进行模型构建,并依据判定系数(R2)和均方根误差(RMSE)来描述模型的精度,用剩下的30%的数据对模型进行检验。
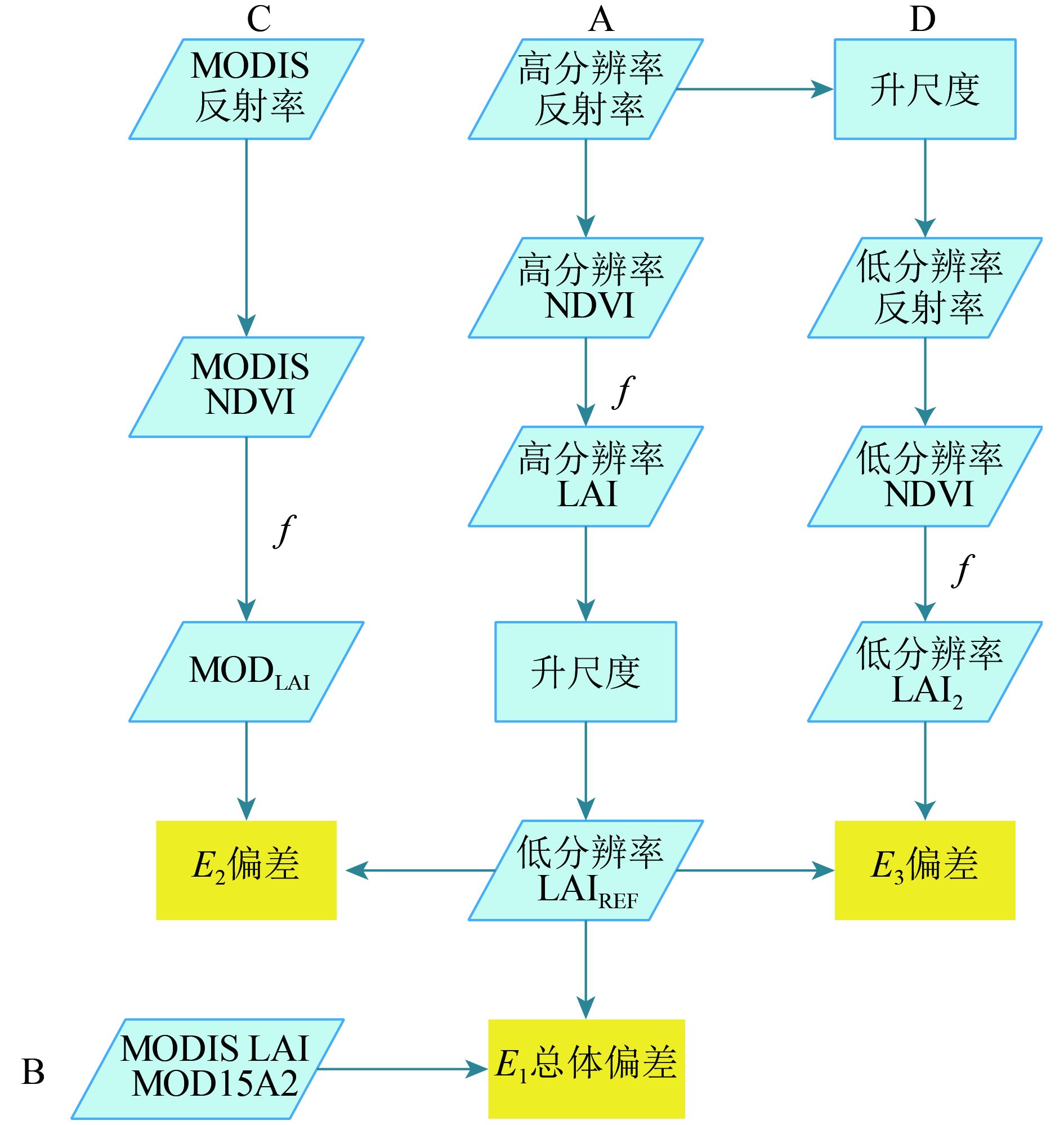
2.3.2. MODIS LAI产品真实性检验偏差分析MODIS LAI产品在生产过程中,存在很多与参考数据生产过程不一致的地方。主要有以下3个方面:(1)反演模型差异:参考数据是利用植被指数与LAI之间的半经验的统计模型得到的,而MODIS LAI数据是基于3维辐射传输理论(Privette 等,2002);(2)反射率数据差异:参考数据是基于Landsat 8 OLI地表反射率数据计算的,而MODIS LAI是基于MODIS地表方向反射率数据计算得到的,两个反射率之间的差异最终会导致LAI有所差别;(3)聚集效应:参考数据是在过渡尺度数据基础之上直接升尺度得到的,而MODIS LAI产品是基于空间分辨率为1 km的地表方向反射率计算得到的,即使两者所采用的计算模型一致,聚集效应的存在,使得两者之间存在差异(Ryu 等,2010)。MODIS LAI产品真实性检验的偏差分析基本过程如图2所示。
|
| 图 2 MODIS LAI产品真实性检验与偏差分析流程图(蓝色表示低分辨率LAI的不同计算过程,黄色代表的是偏差分析) Figure 2 Flow diagram of bias analysis of MODIS LAI product (Blue represents different process of low resolution LAI, yellow represents the deviation analysis) |
在流程图2中,函数f是NDVI与LAI之间的半经验模型。各个偏差因素的解释如下:
总体偏差:
| ${E_1} = {\rm{LAI}}_{\rm{REF}} - {\rm{MOD15A2}}$ | (2) |
式中,LAIREF为真实性检验的的参考产品,对应于生产过程A;MOD15A2是待检验的LAI产品,对应于生产过程B。E1即LAIREF产品与MOD15A2产品之间差异为MODIS LAI产品真实性检验的总体偏差,包括反演模型差异、反射率数据差异和聚集效应3个方面。
模型差异对结果造成的偏差:
| $\begin{aligned}{E_1} - {E_2} & = \left( {{\rm{LA}}{{\rm{I}}_{{\rm{REF}}}} - {\rm{MOD}}15{\rm{A}}2} \right) - \\ & \left( {{\rm{LA}}{{\rm{I}}_{{\rm{REF}}}} - {\rm{MO}}{{\rm{D}}_{{\rm{LAI}}}}} \right)\\ & = {\rm{MO}}{{\rm{D}}_{{\rm{LAI}}}} - {\rm{MOD}}15{\rm{A}}2\end{aligned}$ | (3) |
式中,MODLAI利用MODIS的反射率数据,并结合NDVI与LAI之间的半经验模型计算得到的,对应于过程C。E2仅仅包含反射率差异和聚集效应两个因素对真实性检验结果的影响。E1与E2之间的差异就是反演模型这个单一因素对检验结果的影响。
反射率差异对结果造成的偏差:
| $\begin{aligned}{E_2} - {E_3} & = \left( {{\rm{LA}}{{\rm{I}}_{{\rm{REF}}}} - {\rm{MO}}{{\rm{D}}_{{\rm{LAI}}}}} \right) - \\ & \left( {{\rm{LA}}{{\rm{I}}_{{\rm{REF}}}} - {\rm{LA}}{{\rm{I}}_2}} \right)\\ & = {\rm{LA}}{{\rm{I}}_2} - {\rm{MO}}{{\rm{D}}_{{\rm{LAI}}}}\end{aligned}$ | (4) |
式中,LAI2是首先将高分辨率反射率数据采样至MODIS LAI像元尺度,再利用半经验模型计算得到的低分辨率LAI数据,对应于过程D。E3偏差仅仅是由聚集效应引起的,与E2的差值就排除了聚集效应的影响,仅仅剩下反射率数据这个因素对真实性检验结果的影响。
聚集效应对结果造成的偏差:
| ${E_3} = {\rm{LA}}{{\rm{I}}_{{\rm{REF}}}} - {\rm{LA}}{{\rm{I}}_2}$ | (5) |
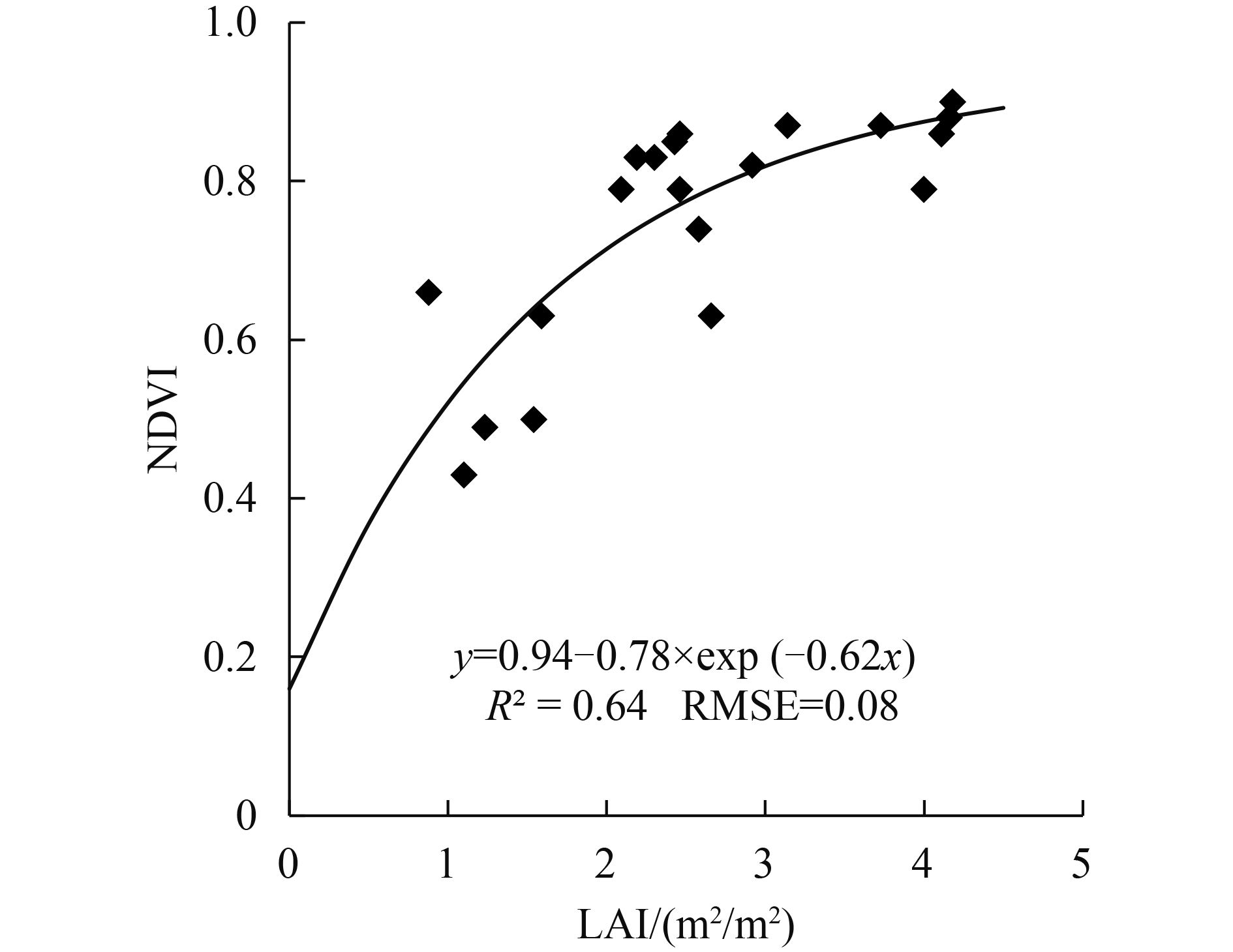
根据在实验期间获得的LAINet地面实测数据和高分辨率遥感数据,构建NDVI与LAI之间的关系如图3所示,该拟合模型的判定系数为0.64,均方根误差为0.08,说明该拟合模型精度比较高,效果比较理想。NDVI与LAI之间的半经验公式为
| ${\rm{NDVI}} = 0.94 - 0.78 \times {\rm{exp}}\left( { - 0.62 \times {\rm{LAI}}} \right)$ | (6) |
|
| 图 3 NDVI和LAI关系图 Figure 3 The relationship of NDVI and LAI |
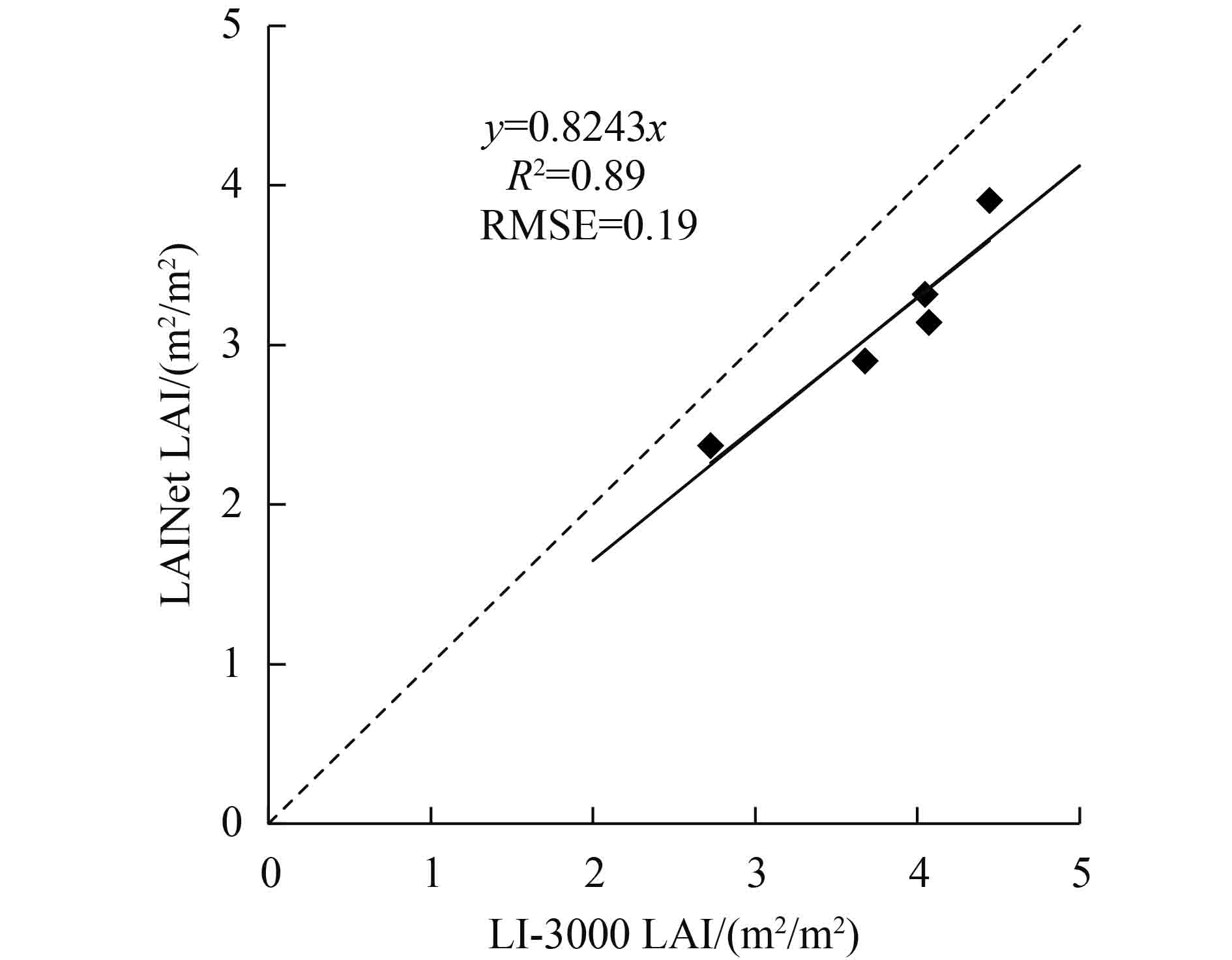
在野外实验期间,通过收割法得到了LAI真实值(LI-3000 LAI)与LAINet的测量结果,对两者的观测结果进行相关分析,如图4所示。需要说明的是,在实验期间,只在试验站附近的样方进了LI-3000和LAINet的对比观测(做破坏性采样对比用)。由于LI-3000是一种手工测量方法,耗时费力,仅在DOY=189/195/205/237/251进行了测量,在DOY=189/195/205,玉米处于生长期,在DOY=237/251时,玉米处于缓慢衰减期。因此,最后仅有5组LI-3000和LAINet的测量数据进行分析、建立关系。
|
| 图 4 LAINet LAI与LI-3000LAI关系图 Figure 4 The relationship of measurements of LI-3000 and LAINet |
LI-3000的测量结果为真实LAI,LAINet的测量结果为有效LAI。从图4可以看出两者之间的判定系数为0.89,均方根误差仅为0.19,相关性高达0.94。这表明LAINet的测量结果具有较高的可信度。在本研究中我们借助该关系式把有效LAI转换为真实LAI。
| ${\rm{LA}}{{\rm{I}}_{\rm t}} = {\rm{LA}}{{\rm{I}}_{\rm e}}/0.8243$ | (7) |
式中,LAIt与LAIe分别代表真实LAI与有效LAI。利用上述式(6)与式(7),并结合高分辨率NDVI数据,计算得到过渡尺度LAI。
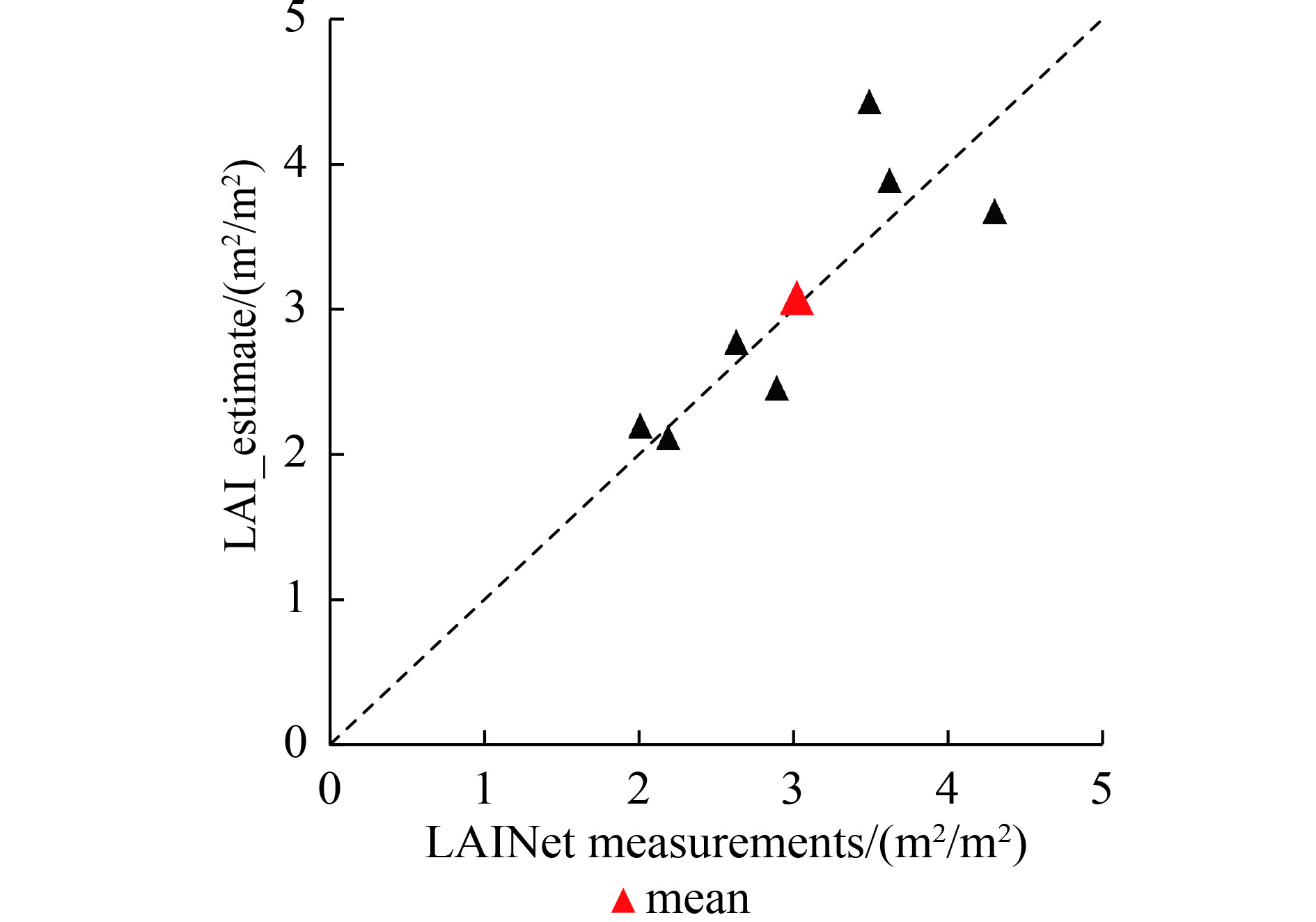
在本文中,利用地面实测LAI与高分辨率NDVI数据构建转换关系,从而得到高分辨率的LAI数据。受限于OLI数据的限制,只有3景OLI影像,地面实测数据的选择也受限于高分影像的时相。我们随机选择70%的地面实测数据构建转换关系,用剩下的30%实测数据对过渡尺度LAI数据进行精度检验,如图5所示。可以看出数据基本上分布在1∶1附近,检验数据与过渡尺度LAI数据的均值分别为3.02 m2/m2、3.08 m2/m2,相对误差仅为1.98%,平均相对误差为11.70%。说明过渡尺度LAI数据是可靠的,可以作为参考数据对MODIS LAI产品进行真实性检验。
|
| 图 5 过渡尺度LAI精度检验 Figure 5 The scatter diagram between 30% field LAI and corresponding high resolution LAI |
将过渡尺度LAI聚合至MODIS LAI产品尺度,并将其作为参考产品,对MODIS LAI进行真实性检验。表4为研究区3个DOY参考LAI与MODIS LAI数据的统计结果,图6为MOD15A2产品的真实性检验结果,图7为参考数据与MODIS LAI数据的箱式图。
|
|
表 4 参考数据和MODIS LAI数据统计结果 Table 4 Statistical result of reference LAI and MODIS LAI product |
|
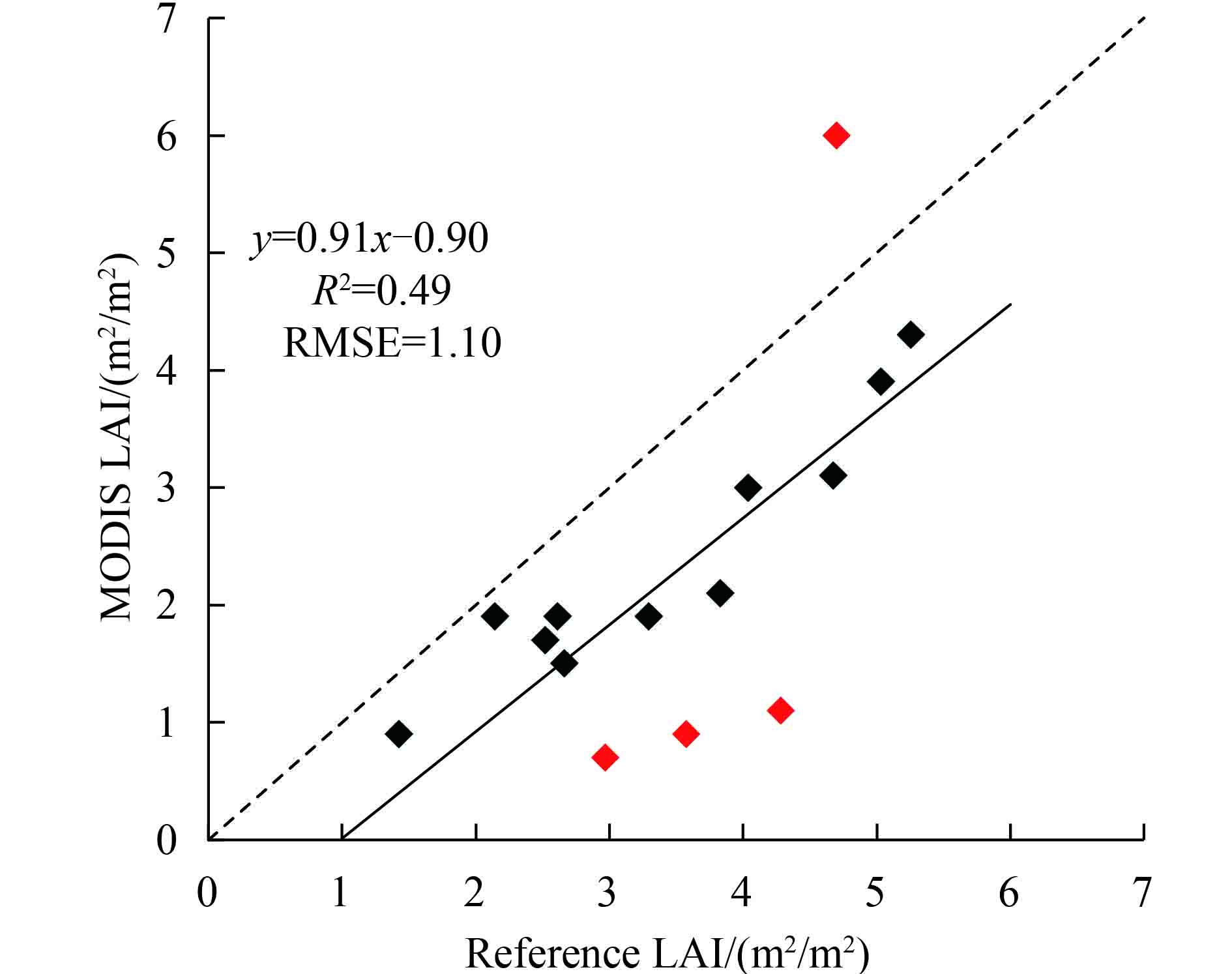
| 图 6 MODIS LAI产品真实性检验结果(红色为异常值) Figure 6 The validation result of MODIS LAI product (red is abnormal value) |
|
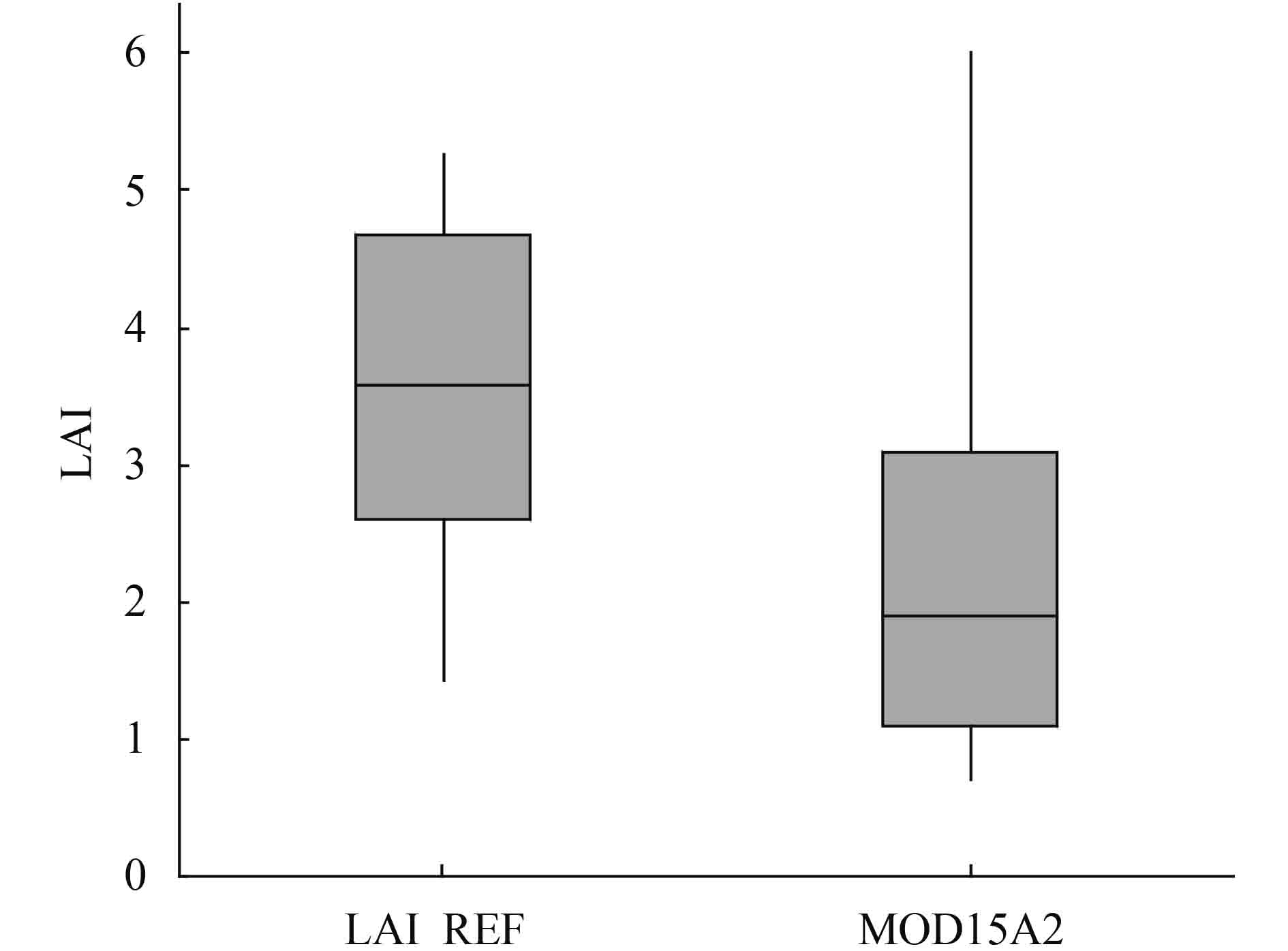
| 图 7 参考产品与MODIS LAI产品箱式图 Figure 7 The boxplot of reference LAI and MODIS LAI |
从表4可以看出,该研究区参考LAI数据范围为1.42—5.26 m2/m2,MODIS LAI产品在0.70—6.00 m2/m2之间,具有较大的变异程度。参考数据的均值为3.53 m2/m2,标准差为1.14 m2/m2,MODIS LAI数据的均值为2.33 m2/m2,标准差为1.48 m2/m2。就均值而言,MODIS LAI产品低估约为34.14%。从图6可以看出,MODIS LAI数值整体上位于1∶1线下方,亦说明MODIS LAI产品存在低估现象。从图7箱式图中也可以直观地看出,MODIS LAI数据的分布较为分散,数据的变异程度比较大,同时也可以看出MODIS LAI数据相对于参考数据而言存在一定程度的低估现象。
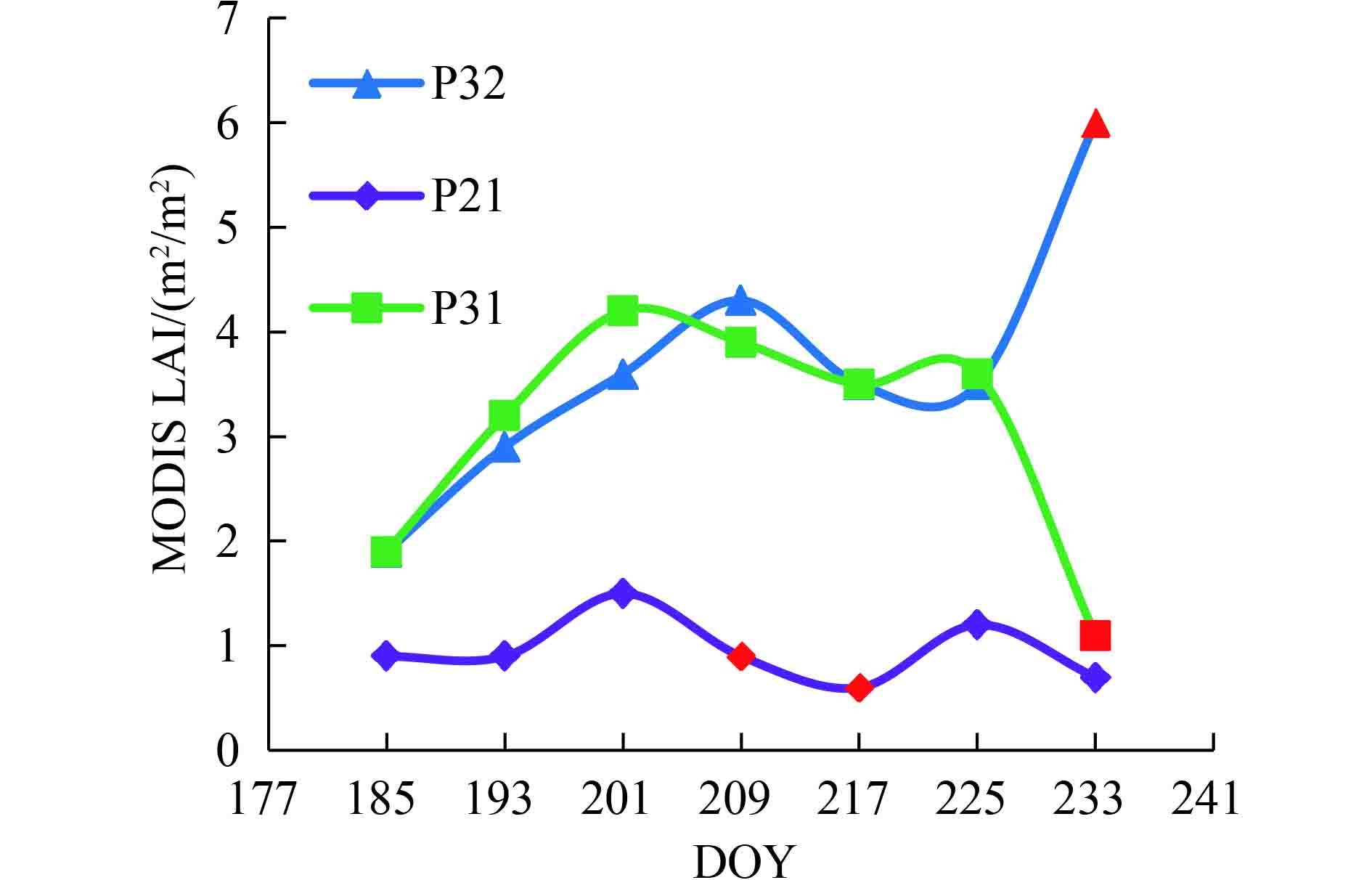
另外,从图6中可以看出,MODIS LAI数据存在1个异常高估和3个低估较为严重的数据。为了对其进行更加准确的说明,对参与检验的MODIS LAI像元进行编号(如“P32”代表第3行第2列的像元),提取异常像元在时间序列上的趋势,如图8所示。
|
| 图 8 异常像元时间序列图 Figure 8 Time series of three abnormal MODIS LAI pixels |
可以看出,“P32”像元在DOY=233时存在急剧增加的现象,由3.50 m2/m2增加为6.00 m2/m2,相对于参考LAI4.70 m2/m2,其高估程度高达27.68%;“P31”像元在DOY=233时存在迅速减少的现象,由3.60 m2/m2降低为1.10 m2/m2,参考数据为2.97 m2/m2;“P21”像元由于含有部分水体与建筑物等,造成该像元空间异质性较强,使得LAI值整体偏低。真实性检验结果表明“P21”像元在DOY=209和233存在低估现象,但是在时间序列上并不明显。
由于MODIS LAI产品在像元“P11—P13”以及“P22”没有有效数据,因此真实性检验以及偏差分析均不包含以上4个像元(图9(a)中蓝色像元)。

|
| 图 9 偏差分析 Figure 9 Analysis of bias |
从偏差分布图中可以明显看出,偏差基本上都是正值,即MODIS LAI数据要小于参考数据,但是“P32”像元在DOY=233时,存在一个明显的负值。通过偏差分布直方图,我们可以得到,偏差分布在0—0.5 m2/m2之间的仅有14.29%,在0.5—1.0 m2/m2之间所占比重最大,为35.71%,位于1.0—1.5 m2/m2之间的为21.43%。
(3.3) MODIS LAI产品的时间序列分析利用地面实测LAI数据对MODIS LAI产品在时间序列上进行真实性检验。我们将实验期间整个研究区上的实测数据进行平均,得到整个研究区的LAI均值,以此作为参考数据。将待检验的MODIS LAI产品在研究区范围内进行平均,分别得到DOY=185/193/201/209/217/225/233的产品值。
|
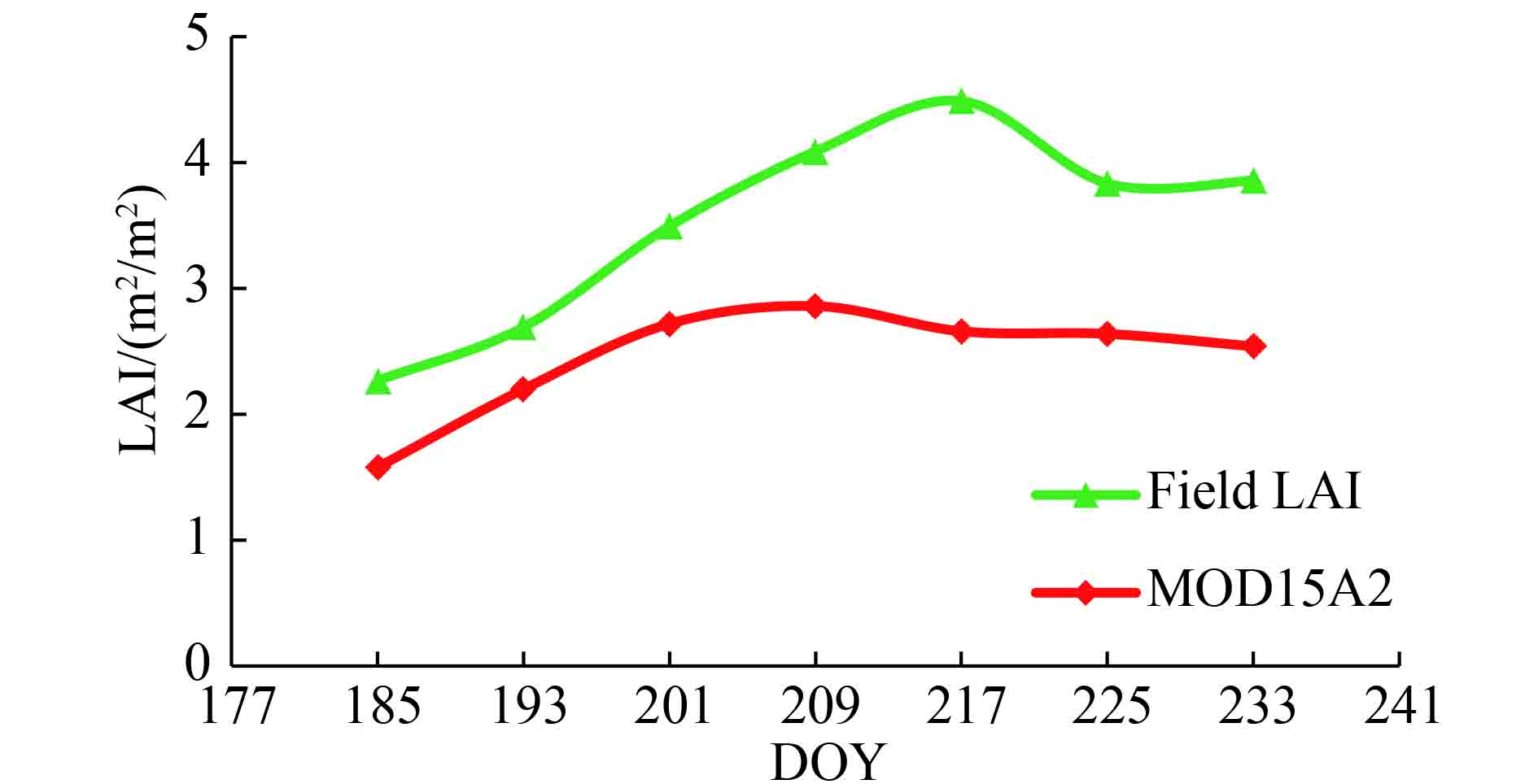
| 图 10 MODIS LAI产品时间序列检验 Figure 10 Temporal validation of MODIS LAI product |
|
|
表 5 MODIS LAI产品时间序列上与实测数据比较 Table 5 Comparison between field LAI and MODIS LAI at study area |
从图10可以看出,实测数据和MODIS LAI数据在时间趋势上具有较好的一致性,能够反映玉米的基本生长趋势。MODIS LAI数据从DOY=185到DOY=209一直处于快速的增长阶段,之后处于稳定期并有微弱的减小趋势,而实测数据在DOY=217之前一直处于快速增加阶段,到达峰值后,存在较大的下降趋势,从4.49 m2/m2减小到3.83 m2/m2(表5)。究其原因,实测数据是以点的形式进行观测的,与MODIS LAI数据在观测尺度上存在很大差异,另外,天气等因素都会对实测数据造成不同程度的影响。
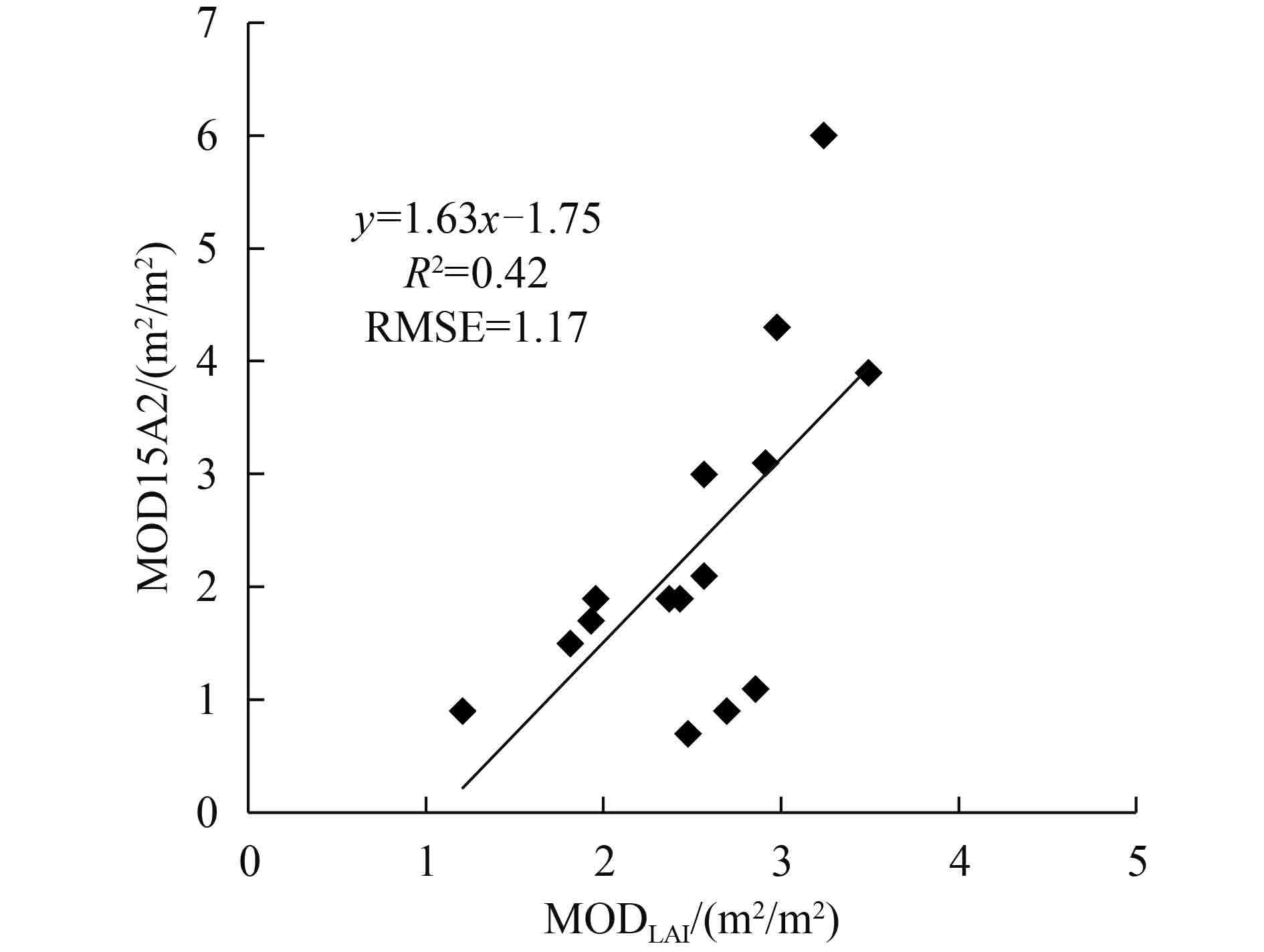
(3.4) MODIS LAI产品偏差分析结果 3.4.1. 反演模型差异对真实性检验结果的影响按照图2所示的流程来分析由于LAI计算模型差异对LAI真实性检验结果的影响。MODIS LAI产品主算法是利用MODIS的地表方向反射率数据,相应的太阳和传感器角度信息、土地覆盖类型等数据,基于3维辐射传输理论计算LAI;备用算法是基于NDVI与LAI的关系来估算LAI值。本文的参考LAI数据是利用NDVI-LAI半经验模型计算的,该模型与MODIS LAI产品主算法之间的差异会直接体现在LAI真实性检验结果中。图11为MODLAI数据与MOD15A2数据之间的散点图,MODLAI数据的均值为2.50 m2/m2,MOD15A2数据的均值为2.33 m2/m2,就均值而言,由于模型的不一致,对检验结果造成0.17 m2/m2的影响,占总偏差的14.17%。
|
| 图 11 参考数据和MODIS LAI产品模型对比 Figure 11 Model comparison between reference LAI and MODIS LAI |
根据图2的流程,分析Landsat 8 OLI地表反射率(聚合至1 km)与MOD09A1反射率数据的差异对于真实性检验结果的影响(图12)。
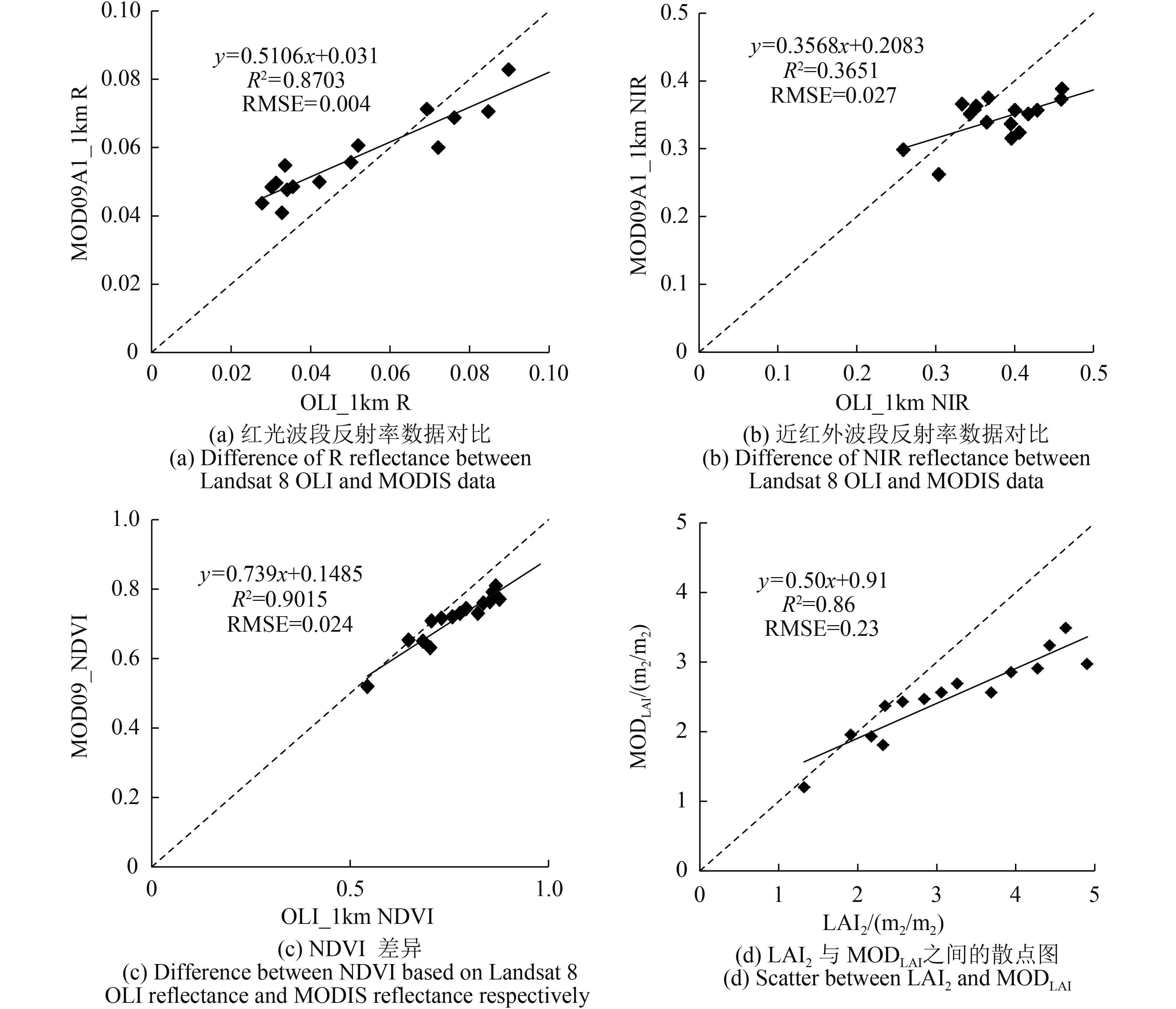
从图12(a)(b)可以看出,OLI地表反射率与MOD09A1地表反射率在红波段具有较好的一致性,但是在近红外波段两者的一致性较差,数据大部分位于1∶1线下方。这主要是由两者光谱响应差异,大气校正差异以及观测日期之间的差异等因素造成的。由于NDVI可以有效突出植被信息,基于两者的反射率数据分别计算NDVI并进行对比分析,发现两者NDVI之间存在很好的一致性,但是OLI_1km NDVI整体上要比MOD09 NDVI偏高,其在表达植被信息上更加具有优势(图12(c))。
为了定量分析OLI和MOD09反射率之间的差异对LAI真实性检验的影响,基于计算的NDVI数据,利用构建的半经验模型计算低分辨率LAI2和MODLAI,两者之间的差异就体现了由于反射率数据差异对LAI验证结果的影响。图12(d)为LAI2与MODLAI之间的散点图,可以看出MODLAI数据在整体上要小于LAI2数据,MODLAI数据的均值为2.50 m2/m2,LAI2数据的均值为3.19 m2/m2,两者相差0.69 m2/m2,即由于反射率数据的差异,造成MODIS LAI产品存在低估现象,且占总偏差的57.50%。从结果可以看出,反射率数据对真实性检验结果的影响是较大的,是引起MODIS LAI产品不确定性的主要因素之一,其与传感器类型、成像时的角度信息、天气以及大气校正算法等因素是密切相关的。由于LAI属于植被冠层结构参数,从3维辐射传输方程的角度来看,近红外波段反射率对LAI数值变化更为敏感。因此,本文产品验证结果为算法研究者提供了一个改进产品算法的信息,即提高原始反射率数据,尤其是近红外波段的精度,将会大大提高LAI产品反演精度。
|
| 图 12 Landsat 8 OLI与MODIS反射率之间差异 Figure 12 Difference between Landsat 8 OLI reflectance and MODIS reflectance |
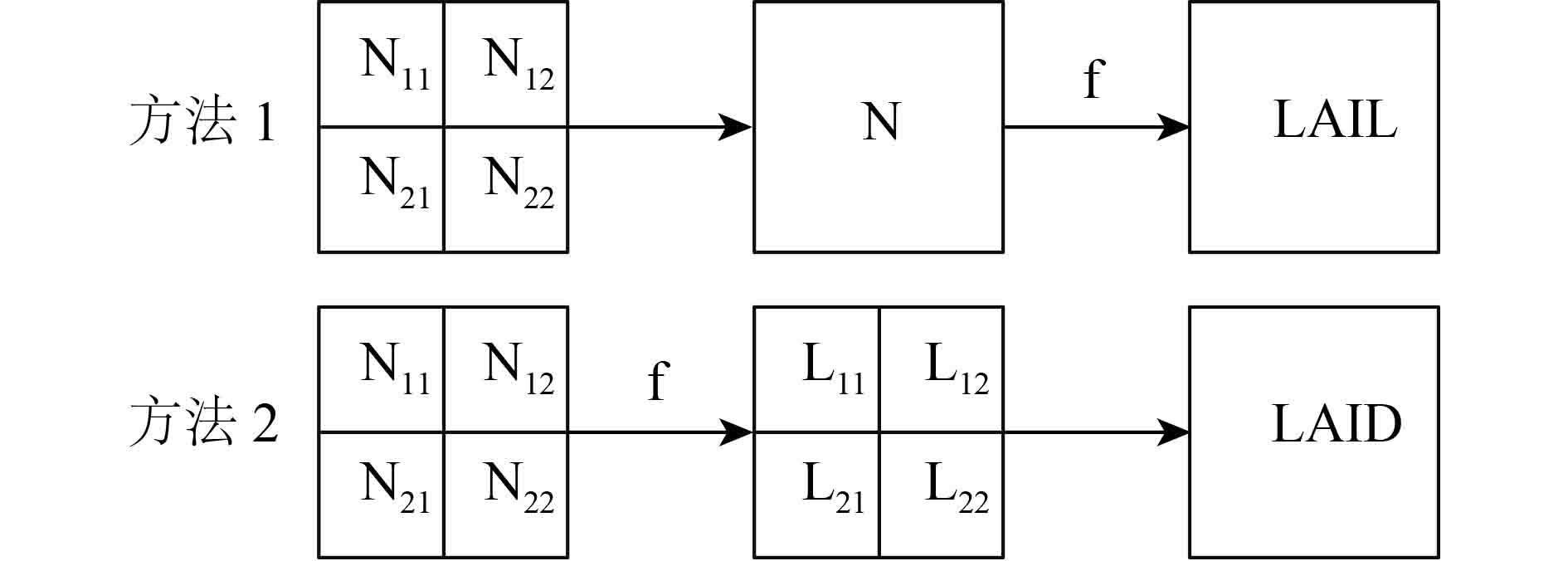
图13表达了由NDVI反演LAI的两种不同的过程。方法一是先将小像元的NDVI平均为大像元的NDVI,再由此大像元的平均NDVI反演为LAI,称为“先平均后反演”;方法二是先将小像元NDVI反演成LAI,再由小像元的LAI平均为大像元的LAI,称其为“先反演后平均”(张仁华 等,2010)。由于聚集效应的存在,使得这两种大尺度LAI计算结果之间存在一定的差异。
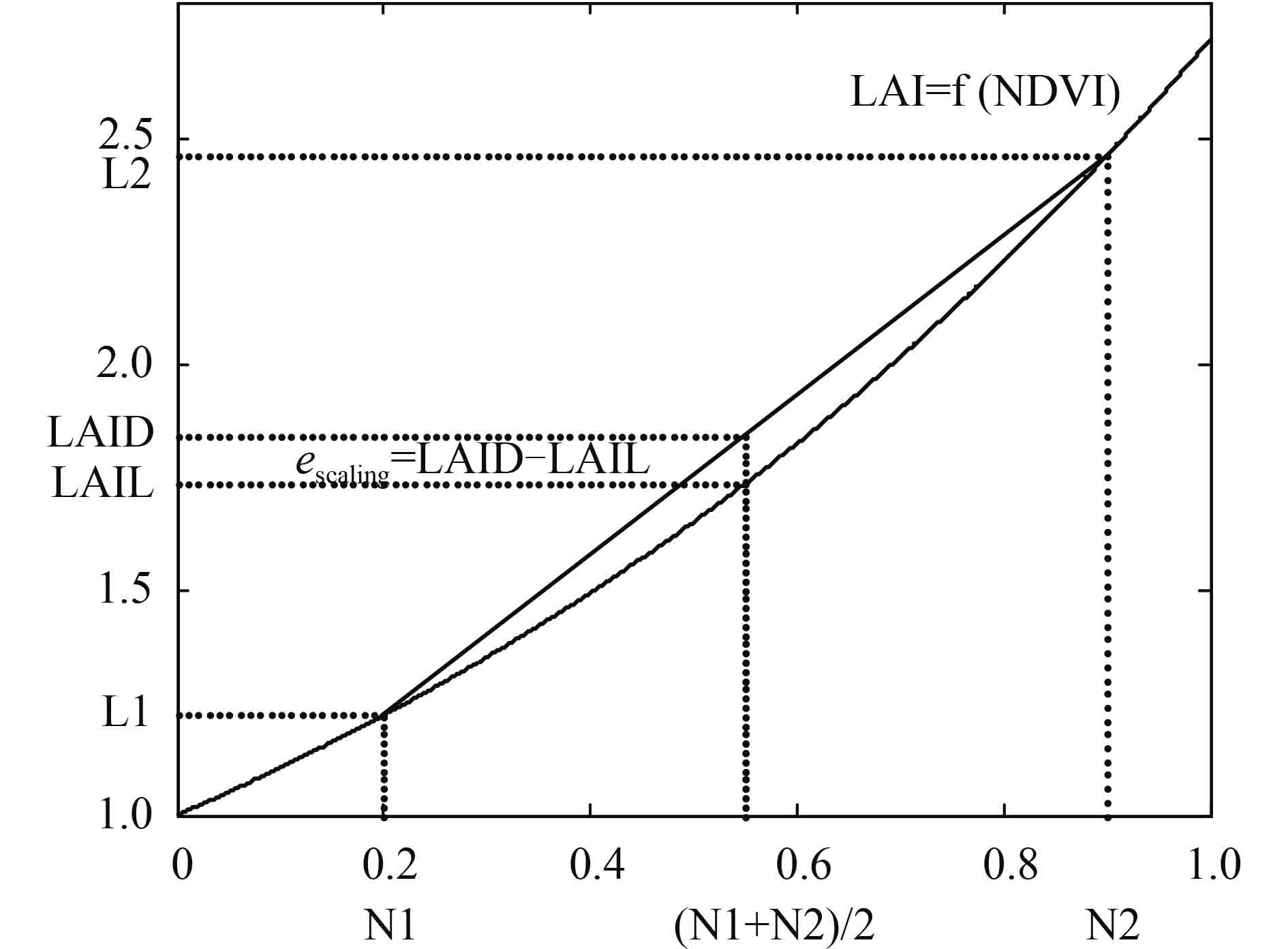
在图14中,f为LAI与NDVI之间的非线性关系式,假设两个小像元的NDVI值分别为N1和N2,根据LAID的计算过程,先计算小像元的LAI值,分别为L1和L2,再聚合得到大像元的LAI值,为(L1+L2)/2,在图中直观的展示为梯形的中位线;根据LAIL的计算过程,先聚合得到大像元的NDVI值为(N1+N2)/2,再利用函数f计算大像元的LAI值。从图14中可以直观地看出,escaling为LAID与LAIL之间的差异。
|
| 图 13 两种常用的LAI聚集方法(N代表NDVI;L代表LAI;LAIL为集总式LAI;LAID为分布式LAI) Figure 13 Two kinds of frequently-used methods in LAI upscaling (N represents NDVI; L represents LAI; LAIL: Lumped LAI; LAID: Distributed LAI) |
|
| 图 14 LAIL与LAID之间的差异 Figure 14 Differences between LAIL and LAID due to non-linear of f and heterogeneity |
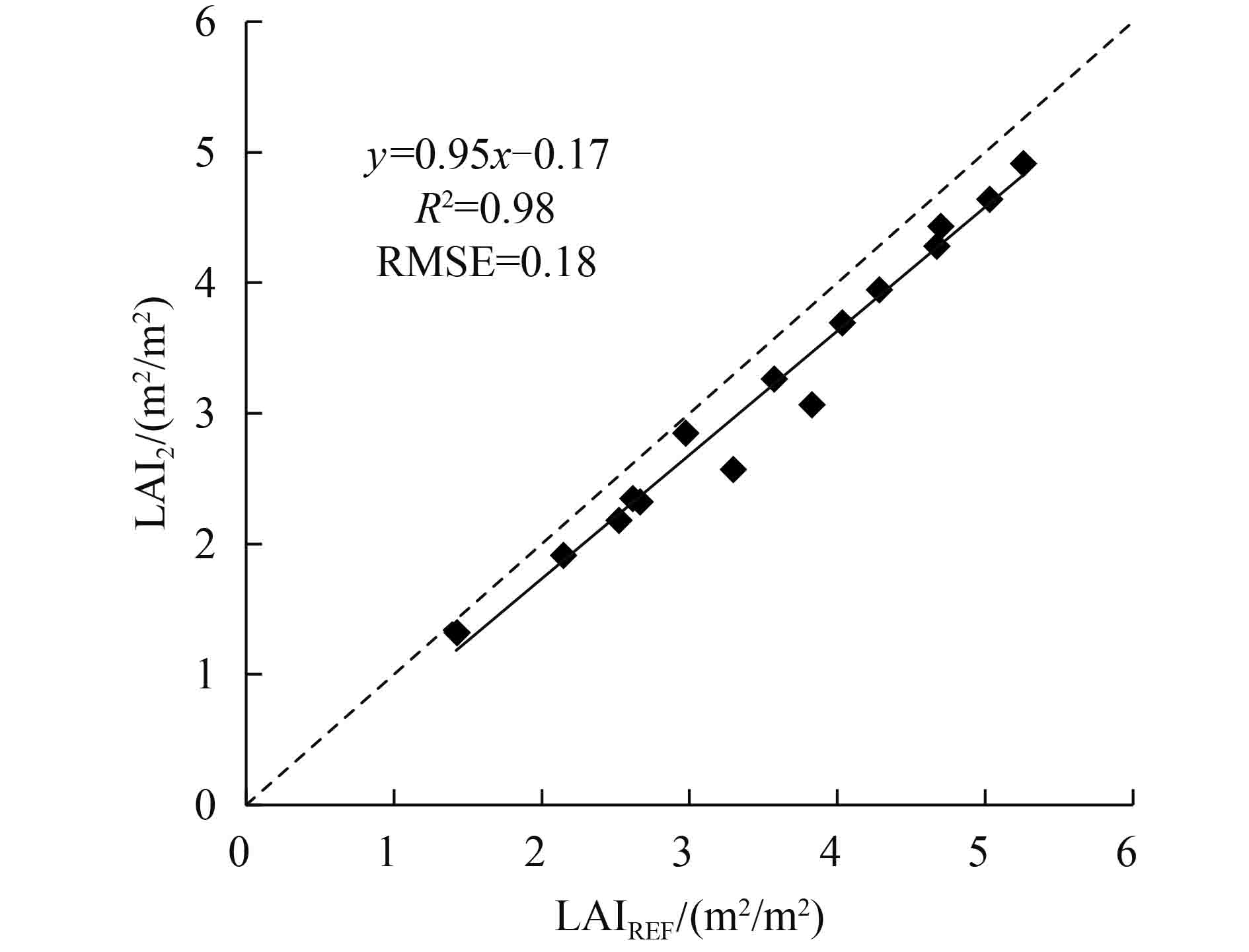
从以上的分析可知,MODIS LAI产品与参考产品之间存在聚集效应,那么,聚集效应MODIS LAI产品真实性检验结果的影响究竟有多大?为了将这个影响定量化,根据图2的流程图来进行分析。图15为参考数据与LAI2数据之间的散点图,可以看出,LAI2数据整体上小于参考数据,说明聚集效应对检验结果造成了低估的现象。参考数据的均值为3.53 m2/m2,LAI2数据的均值为3.19 m2/m2,两者相差0.34 m2/m2,即聚集效应对检验结果造成了的偏差占总偏差的28.33%。可以看出聚集效应是引起MODIS LAI产品不确定性的主要因素之一,也是限制MODIS LAI产品在实际应用中的瓶颈之一。
然而,还需要指出的是,聚集效应是影响不同分辨率产品尺度效应的因素之一。其他因素,如混合像元现象、传感器的点扩散函数等多个方面都会影响到尺度效应。本文仅从聚集效应的角度进行了初步分析。在后期的研究工作总,将会考虑到不同因素的影响,更深入地进行尺度效应分析。
|
| 图 15 聚集效应 Figure 15 Clumping effect analysis |
MODIS LAI产品真实性检验过程中存在很多不确定性因素,在结果中需要定量评价这些因素的贡献。本文在对MODIS LAI产品进行真实性检验基础上,进一步将其不确定性因素归纳为反演模型差异、反射率数据差异和聚集效应3个方面,并定量表达这三个因素对真实性检验结果的影响,提出了中低分辨率卫星产品真实性检验、偏差分析的基本流程,对卫星产品真实性检验具有一定的借鉴意义。研究结果表明:
(1) 该区域MODIS LAI产品存在明显的低估现象,参考数据和MODIS LAI数据均值分别为3.53 m2/m2和2.33 m2/m2,MODIS产品低估为34.14%。
(2) 反射率数据是造成MODIS LAI产品低估的最大影响因素,占总偏差的57.50%。由于MODIS数据的空间分辨率较低,使得很多农作物区域的MODIS像元成为混合像元,包含道路、水体和建筑物等地物类型,这些地物类型尤其是在近红外波段的反射率要远低于玉米冠层的反射率,使得混合像元的总体反射率较低,造成MODIS LAI像元值偏低,即空间异质性是影响MODIS LAI产品质量的主要因素之一。这与已有研究结果是一致的(胡少英和张万昌,2005;杨飞 等,2010;朱小华 等,2010)。
(3) 聚集效应对MODIS LAI产品真实性检验结果的影响也较大,对总偏差的影响为28.33%。由于聚集效应的存在,使得MODIS LAI产品存在低估现象,这主要是由于反演LAI的算法非线性引起的,与前人有相同的研究结果(Garrigues 等,2006;刘良云,2014;孙晨曦 等,2014),只是低估程度不尽相同。
(4) 模型差异对检验结果最小,占总偏差的14.17%。已有研究结果指出,影响MODIS LAI产品质量的一个主要因素是建立查找表的物理模型的不确定性,但是并未定量化该不确定性。孙晨曦等人(2004)的研究结果表明MODIS LAI模型高估约为44.2%,与本研究有相反的结论,这是由于所采用的回归模型和检验对象不一致造成的。由此,也可以看出,在不同的检验区域,采用不同的回归模型得到的结果不尽相同。
从本研究的流程可以看出,对MODIS LAI产品的真实性检验及偏差分析都是以参考数据作为标准的,参考数据的精度对研究结果有直接的影响。如何提高参考数据的精度是下一步工作的重点。另外,地面实测数据是开展卫星产品真实性检验工作的基础,如何减小实测数据的不确定性,如何获取空间异质性条件下的LAI实测数据还有待进一步的研究。
志 谢 感谢遥感科学国家重点实验室怀来遥感试验场的柏军华助理研究员,肖青研究员工作人员为获取野外数据提供的帮助,如有读者对论文中的部分实验数据感兴趣,可以联系通信作者索取。
| [1] | F Baret, G Guyot. Potentials and limits of vegetation indices for LAI and APAR assessment[J]. Remote Sensing of Environment, 1991, 35 (2/3) : 161 –173. DOI: 10.1016/0034-4257(91)90009-U |
| [2] | M ChenJ, A BlackT. Defining leaf area index for non-flat leaves[J]. Plant, Cell and Environment, 1992, 15 (4) : 421 –429. DOI: 10.1111/j.1365-3040.1992.tb00992.x |
| [3] | J M Chen, G Pavlic, L Brown, J Cihlar, S G Leblanc, H P White, R J Hall, D R Peddle, D J King, J A Trofymow, E Swift, J Van der Sanden, PKE Pellikka. Derivation and validation of Canada-wide coarse-resolution leaf area index maps using high-resolution satellite imagery and ground measurements[J]. Remote Sensing of environment, 2002, 80 (1) : 165 –184. DOI: 10.1016/S0034-4257(01)00300-5 |
| [4] | 方秀琴, 张万昌, 刘三超. 黑河流域叶面积指数的遥感估算[J]. 国土资源遥感, 2004 (1) : 27 –31. Q FangX, C ZhangW, C LiuS. The estimation ofLAI in Heihe river basin using remotely sensed data[J]. Remote Sensing for Land and Resources, 2004 (1) : 27 –31. |
| [5] | S Garrigues, D Allard, F Baret, D Weiss. Influence of landscape spatial heterogeneity on the non-linear estimation of leaf area index from moderate spatial resolution remote sensing data[J]. Remote Sensing of Environment, 2006, 105 (4) : 286 –298. DOI: 10.1016/j.rse.2006.07.013 |
| [6] | 胡少英, 张万昌. 黑河及汉江流域MODIS叶面积指数产品质量评价[J]. 遥感信息, 2005 (4) : 22 –27. Y HuS, C ZhangW. A quality assessment of MODIS LAI product in Heihe and Hanjiang river basins[J]. Remote SensingInformation, 2005 (4) : 22 –27. |
| [7] | Jin H, Li A N, Bian J H, Lei G B, Tan J B and Xia H M. 2014. Validation of MODISglobal LAI products in forested terrain //Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS).Quebec City:IEEE: 3053–3056 [DOI: 10.1109/IGARSS.2014.6947121] |
| [8] | Z W Li, H Tang, X P Xin, B H Zhang, D L Wang. Assessmentof the MODIS LAI product using ground measurement data and HJ-1A/1B imagery in the meadow steppe of Hulunber, China[J]. Remote Sensing, 2014, 6 (7) : 6242 –6265. DOI: 10.3390/rs6076242 |
| [9] | 刘良云. 叶面积指数遥感尺度效应与尺度纠正[J]. 遥感学报, 2014, 18 (6) : 1158 –1168. Y LiuL. Simulation and correction of spatial scaling effects for leaf area index[J]. Journal of Remote Sensing, 2014, 18 (6) : 1158 –1168. DOI: 10.11834/jrs.20144103 |
| [10] | J T Morisette, F Baret, J L Privette, R B Myneni, J E Nickeson, S Garrigues, N V Shabanov, M Weiss, R A Fernandes, S G Leblanc, M Kalacska, G A Sanchez-Azofeifa, M Chubey, B Rivard, P Stenberg, M Rautiainen, P Voipio, T Manninen, A N Pilant, T E Lewis, J S Iiames, R Colombo, M Meroni, L Busetto, W B Cohen, D P Turner, E D Warner, G W Petersen, G Seufert, R Cook. Validation of global moderate-resolution LAI products: a framework proposed within the CEOS land product validation subgroup[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44 (7) : 1804 –1817. DOI: 10.1109/TGRS.2006.872529 |
| [11] | MR Pandya, R P Singh, K N Chauhari, G D Bairagi, R Sharma, VK Dadhwal, J S Parihar. Leaf area index retrieval using IRS LISS-III sensor data and validation of the MODIS LAI product over central India[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44 (7) : 1858 –1865. DOI: 10.1109/TGRS.2006.876028 |
| [12] | J L Privette, R B Myneni, Y Knyazikhin, M Mukelabai, G Roberts, Y Tian, Y Wang, S G Leblanc. Early spatial and temporal validation of MODIS LAI product in the Southern Africa Kalahari[J]. Remote Sensing of Environment, 2002, 83 (1/2) : 232 –243. DOI: 10.1016/S0034-4257(02)00075-5 |
| [13] | 屈永华, 王锦地, 董健, 姜富斌. 农作物冠层结构参数自动测量系统设计与试验[J]. 农业工程学报, 2012, 28 (2) : 160 –165. Y H Qu, J D Wang, J Dong, F B Jiang. Design and experimentof crop structural parameters automatic measurement system[J]. Transaction of the CSAE, 2012, 28 (2) : 160 –165. |
| [14] | 屈永华. 2013. 河北怀来试验站玉米LAINet观测数据集. 北京: 北京师范大学 Qu Y H. 2013. LAINet Datasets of Cron at Experiment Station at Huaiai, Hebei Province. Beijing: Beijing Normal University |
| [15] | H QuY, Z FuL, C HanW, Q ZhuY, D WangJ. MLAOS: amulti-point linear array of optical sensors for coniferous foliage clumping index measurement[J]. Sensors, 2014a, 14 (5) : 9271 –9289. DOI: 10.3390/s140509271 |
| [16] | Y H Qu, W C Han, L Z Fu, C R Li, J L Song, H M Zhou, J D BoY C andWang. LAINet – A wireless sensor network for coniferous forest leaf area index measurement: design, algorithm and validation[J]. Computers and Electronics in Agriculture, 2014b, 108 : 200 –208. DOI: 10.1016/j.compag.2014.08.003 |
| [17] | H QuY, Q ZhuY, C HanW, D WangJ, G MaM. Crop leafarea index observations with a wireless sensor network and its potential for validating remote sensing products[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014c, 7 (2) : 431 –444. DOI: 10.1109/JSTARS.2013.2289931 |
| [18] | Y Ryu, T Nilson, H Kobayashi, O Sonnentag, B E Law, DD Baldocchi. On the correct estimation of effective leaf area index: does it reveal information on clumping effects?[J]. Agricultural and Forest Meteorology, 2010, 150 (3) : 463 –472. DOI: 10.1016/j.agrformet.2010.01.009 |
| [19] | P SerbinS, E AhlD, T GowerS. Spatial and temporal validation of the MODIS LAI and FPAR products across a boreal forest wildfire chronosequence[J]. Remote Sensing of Environment, 2013, 133 : 71 –84. DOI: 10.1016/j.rse.2013.01.022 |
| [20] | 孙晨曦, 刘良云, 关琳琳, 焦全军, 彭代亮. 锡林浩特草原区域MODIS LAI产品真实性检验与误差分析[J]. 遥感学报, 2014, 18 (3) : 518 –536. X SunC, Y LiuL, L GuanL, Q JiaoJ, L PengD. Validation and error analysis ofthe MODIS LAI product in Xilinhot grassland[J]. Journal of Remote Sensing, 2014, 18 (3) : 518 –536. DOI: 10.11834/jrs.20143097 |
| [21] | H TianY, E WoodcockC, J WangY, L PrivetteJ, V ShabanovN, R ZhouLM, B ZhangY. Multiscale analysis and validation of the MODIS LAI product: I[J]. Uncertainty assessment. Remote Sensing of Environment, 2002, 83 (3) : 414 –430. DOI: 10.1016/S0034-4257(02)00047-0 |
| [22] | J WangY, E WoodcockC, H BuermannW, N StenbergP, B VoipioP. Evaluation of the MODIS LAI algorithm at a coniferous forest site in Finland[J]. Remote sensing of Environment, 2004, 91 (1) : 114 –127. DOI: 10.1016/j.rse.2004.02.007 |
| [23] | 吴小丹, 肖青, 闻建光, 刘强, 彭菁菁, 李小文. 遥感数据产品真实性检验不确定性分析研究进展[J]. 遥感学报, 2014, 18 (5) : 1011 –1023. X D Wu, Q Xiao, J G Wen, Q Liu, J J Peng, X W Li. Advancesin uncertainty analysis for the validation of remote sensing products: take leaf area index for example[J]. Journal of Remote Sensing, 2014, 18 (5) : 1011 –1023. DOI: 10.11834/jrs.20143332 |
| [24] | 杨飞, 孙九林, 张柏, 姚作芳, 王宗明, 王卷乐, 乐夏芳. 基于PROSAIL模型及TM与实测数据的MODISLAI精度评价[J]. 农业工程学报, 2010, 26 (4) : 192 –197. F Yang, J L Sun, B Zhang, Z F Yao, Z M Wang, J L Wang, X F Yue. Assessment of MODIS LAI product accuracy based on the PROSAIL model, TM and field measurements[J]. Transaction of the CSAE, 2010, 26 (4) : 192 –197. |
| [25] | W Z Yang, B Tan, D Huang, M Rautiainen, N V Shabanov, Y J Wang, J L Privette, K F Huemmrich, R Fensholt, I Sandholt, M Weiss, DE Ahl, ST Gower, RR Nemani, Y Knyazikhin, RB Myneni. MODIS leaf area index products: from validation to algorithm improvement[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44 (7) : 1885 –1898. DOI: 10.1109/TGRS.2006.871215 |
| [26] | 张仁华, 田静, 李召良, 苏红波, 陈少辉. 定量遥感产品真实性检验的基础与方法[J]. 中国科学: 地球科学, 2010, 40 (2) : 211 –222. RH Zhang, J Tian, Z L Li, H B Su, S H Chen. Principles andmethods for the validation of quantitativeremote sensing products[J]. Science ChinaEarth Sciences, 2010, 40 (2) : 211 –222. DOI: 10.1007/s11430-010-0021-3 |
| [27] | 朱小华, 冯晓明, 赵英时, 宋小宁. 作物LAI的遥感尺度效应与误差分析[J]. 遥感学报, 2010, 14 (3) : 579 –592. H ZhuX, M FengX, S ZhaoY, N SongX. Scale effect and error analysis of crop LAI inversion[J]. Journal of Remote Sensing, 2010, 14 (3) : 579 –592. |

