2. 北京语言大学 图书馆, 北京 100083
2. Library of Beijing Language and Culture University, Beijing 100083, China
0 引言
实体解析(entity resolution) 是辨析、判别数据集中的哪些实体(entity) 的参考表示(references) 指向现实世界中同一个实体的过程[1]. 与聚类、分类、关联规则等数据挖掘任务不同, 实体解析不是传统的数据挖掘任务,而是数据预处理阶段的数据清理过程, 是数据挖掘、信息融合等领域的一个难点问题[2]. 由于不同数据来源的结构 差异等原因, 使得许多数据都具有不确定性和噪声, 数据集中可能存在对同一个实体的不同表示,面对这种情况,通过 对对象进行实体解析可以帮助清洗数据和发现对象之间的潜在关系.
实体解析在多个领域都有实际应用,叫法也略有不同[1, 3]. ① 医疗领域,实体解析用于从医学数据中发现哪些病例记 录指向现实世界中同一个病人或同一个家庭,叫做记录链接(record linkage)[4],这是实体解析最早的应用. ② 计算机视觉领 域, 实体解析则用于识别同一张图像中的哪些区域是同一个对象的组成部分, 称为对应问题(correspondence problem). ③ 自然语言处理领域, 实体解析则用来判断哪些名词短语指的是同一个实体, 称为共引解析(coreference resolution) 或者对象合并 (object consolidation). ④ 数据库领域, 判断同一个数据库或者不同数据库中的两个元组是否是指向同一个实体的重复数 据,称为重复数据删除和数据集成(deduplication and data integration).
实体解析既可以采用监督学习方法,也可以采用非监督学习方法. 二者区别在于前者需要训练数据, 而后者不需要.目前研究主要关注非监督实体解析方法, 主要分为以下三类[3]:
1) 基于属性的方法(attribute-based approaches), 根据每对实体参考表示的属性值计算其相似性, 认为满足相似性阈值的实体表示对是某一实体的共同引用(coreferent).
实体通过若干属性来刻画,属性或属性组合可以具有一定的识别能力. 具有较强识别能力属性或属性组合可以作为实体识别符 (entity identifiers),例如身份证号码、姓名和出生日期、移动电话号码. 而其他识别能力较弱的属性或属性组合则不能作 为实体识别符, 例如出生年份、家庭住址、公司住址. 基于属性的方法首先根据实体属性的取值类型采用相应的相似性度量方 法, 例如: 对于数值型属性的相似性度量可以采用余弦相似度、欧几里得距离; 对于二值型属性的相似性度量可以采用Jaccard 系数[5]; 对于字符型属性的相似性度量可以采用Jaccard 系数、Jaro[6]、Jaro-Winkler[7]、Levenstein[8] (又称edit distance,编辑距离)、Monge-Elkan[9]等. 然后, 使用各种类型属性相似性的加权组合来确定由混合 型属性描述的实体之间的相似性.
基于属性的方法是处理实体解析的传统方法, 可以直接采用传统计算对象相似性的方法进行计算,原理较为简单,已广 泛用于图和关系型数据库进行实体识别. 其缺点是算法复杂度较高, 未能利用实体之间的关系信息,不适用于关系数据.
2) 朴素关系型方法(naive relational approaches), 针对基于属性的方法没有利用实体之间关系的情况, 在实体解析的过程中考虑与实体参考表示相关的实体参考表示, 利用实体之间的链接情况来判断实体的相似性.
朴素关系型方法最早应用于数据库领域[3], Ananthakrishna等人使用链接信息来解决数据仓库应用领域中存在的重复问题, 并且这些链接之间存在维度层次结构[10]; Kalashnikov 等人提出基于关系的数据清理方法RelDC (relationship-based data cleaning)[11], 使用图理论的技术来发现和分析实体参考表示节点之间的附属关系、合 作关系等. 此外,Bhattacharya 等还提出了若干对基于属性的实体解析方法直接进行改进的关系型实体解析方法[1], 实体之间的相似性定义为二者基于属性的实体相似性和基于边(链接) 的实体相似性的线性组合.
朴素关系型实体解析方法在基于属性的实体解析方法的基础上考虑了相互关联实体的属性相似性, 但是每一个实 体的解析仍然是独立进行的.
3) 协同关系型方法(collective relational approaches), 针对现实数据中不同实体的参考表示经常同时出 现的情况, 对相互关联的实体进行联合解析, 即一个实体的解析结果会影响与其相关联的实体解析结果.
进行协同实体解析的一个常用思路是把实体解析当成聚类问题, 将实体参考表示聚成若干个实体类(entity clusters),每一个 实体类对应于现实世界中的一个实体. 两个实体类之间的相似性是二者基于属性的相似性和关系相似性的线性组合[3], 前者由二者包含的实体之间属性相似性的聚集函数决定, 后者由二者包含的实体的邻居集合共有类标签个数决定,度量方法包 括[1]: 共同邻居个数、Jaccard 系数、Adar/Adamic 分值等. 针对此问题,Bhattacharya等提出了一个凝聚型聚类算法[1], 将实体类不断聚集成更大的类, 采用迭代方法对实体及其相关实体联合进行确定. 此外,基于LDA (latent Dirichlet allocation) 模型也可以进行协同实体解析,例如Bhattacharya 等提出的一个基于LDA 的方法,能够根据作者的出版物对作者进行 协同关系实体解析[12].
协同实体解析方法不仅考虑对象及其相关对象的属性信息, 并且相关对象的实体解析判定结果相互影响,这类方法充分利用了同种 对象之间、异种对象之间的关系,因而实体解析准确度较高. 与基于属性和朴素关系型解析方法中两个实体参考表示之间的相似 性是固定不变的情况不同,协同关系型实体解析方法在本质上是动态的, 两个实体类的相似性依赖于它们邻居的现有类标签, 因而会随着类标签的更新而发生变化,准确度较前两种方法有所提高, 但其代价是时间复杂度较高.
此外,现有实体解析问题研究多只关注同一种类型实体的解析, 但是随着包含多种对象的异质网络数据的增多,需要对 异质网络中的不同类型对象同时进行解析. 以文献网络为例, 以往研究往往只关注根据作者的属性或者作者文章的出版 物对作者实体进行解析, 然而实际上同一篇论文的题目在不同数据源中的参考表示也可能不相同, 因此也有必要对论文实体 进行解析. 另外, 效率问题是实体解析的重要问题之一,现有算法时间复杂度一般较高, 例如朴素关系型实体解析算法的时 间复杂度 $O(N^{2}$), 并不适用于大规模数据集.
本文针对包含两种对象的异质网络实体解析问题, 提出了基于联合聚类思想进行实体解析的框架,同时对两种对象进行聚类, 每一个类包含的若干实体参考表示对应于现实世界中的同一个实体. 由于采用联合聚类思想能够同时获得两种对象的聚类结果, 并且避开了同时考虑属性和关系进行相似性计算, 因而在保证实体解析算法准确度的同时降低了算法时间复杂度. 1 概念准备
1.1 对象分类
假定数据集由两种类型实体的不同参考表示构成. 由于不同种类实体的属性取值出现情况不同,在实体解析过程中所起 的作用也不同,因而通过比较方式将两种对象分为决定对象和辅助对象.
定义1 决定对象 (dominant objects,DO) 将两种对象中属性取值较为稳定、不具有较多参考表示的那种实体称为决定对象. 决定对象在实体解析过程中起到决定性作用.
定义2 辅助对象 (assistant objects,AO) 将两种对象中属性取值较为复杂、具有较多参考表示的那种实体称为辅助对象. 辅助对象在实体解析过程中起到辅助性作用.
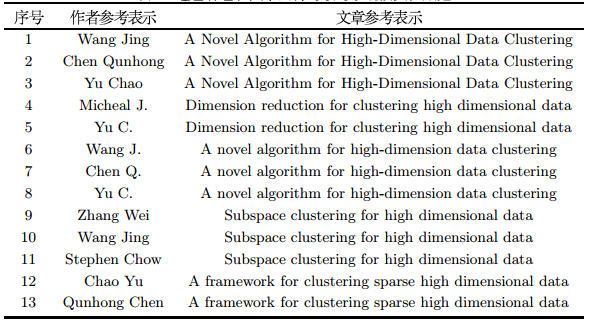
以包含作者和文章两种对象的文献数据为例,一般情况下, 作者实体出现多个参考表示的情况比文章实体出现多个参考表示的情况复杂, 例如作者Wang Fangfang 参与撰写了文章"A Novel Algorithm for High-Dimensional Data Clustering",作者可能的 参考表示有Wang Fangfang、Wang F.、Wang F. F.,而文章可能的参考表示则较为单一. 因此,按照上述对对象 的分类可知, 在对包含作者和文章两种实体的参考表示进行实体解析的过程中, 文章实体是决定对象,作者实体是辅助对象. 1.2 相似性度量
针对具有两种对象的实体解析问题,假设仅已知对象的名称属性, 取值是字符串类型.
定义3 对象相似性度量 (similarity of objects) 假设任意两个对象$S_a$ 和$S_b$,各自包含若干元素(例如,字符、单词), 将$S_a$ 和$S_b$ 的相似性定义为以完全相同元素比例和不完全相同元素比例为系数乘以对应部分相似性的线性组合, 公式如下:
| \begin{equation} S(S_a,S_b)=p_s+(1-p_s)*S_{ns} \end{equation} | (1) |
② $p_s$ 表示字符串$S_a$ 和$S_b$ 具有相同元素占总元素个数的比例,取值范围是$[0,1]$,定义如下:
| \begin{equation} p_s=\frac{\left|S_a\cap{S_b}\right|}{\left|S_a\cup{S_b}\right|} \end{equation} | (2) |
③ $S_{ns}$ 表示字符串$S_a$ 和$S_b$ 不完全相同元素存在相似性的可能性,取值范围是$[0,1]$, 定义如下[13]:
| \begin{equation} S_{ns}=1-\frac{d(l_a,l_b)}{\max(\left|l_a\right|,\left|l_b\right|)} \end{equation} | (3) |
a. 删除操作 (deletion): 从原字符串中任意删去一个字符;
b. 插入操作 (insertion): 在原字符串中任意插入一个字符;
c. 替换操作 (replacement): 任意用一个字符替换原字符串中的一个字符.
示例1 根据定义3,计算文章"A Novel Algorithm for High-Dimensional Data Clustering" 和文章 "A novel algorithm for high-dimension data clustering" 名称的相似性.
按照定义3,计算步骤如下:
① ${S}$$_a$=$\{A,Novel,Algorithm,for,High-Dimensional,Data,Clustering\},$
${S}$$_b$=$\{A,novel,algorithm,for,high-dimension,data,clustering\}.$
求${S}$(${S}$$_a$,${S}$$_b$).
② $S_a\cap{S_b}$=$\{a,novel,algorithm,for,data,clustering\}$,$\left|S_a\cap{S_b}\right|=6$;
$S_a\cup{S_b}$=$\{a,novel,algorithm,for,data, clustering,high-dimensional,high-dimension\}$, $\left|S_a\cup{S_b}\right|=8$;
故由公式(2),得\ $p_s=6/8$,则\ $1-p_s=1-6/8=2/8$.
③由公式(3),可知:
$l_a=S_a\setminus(S_a\cap{S_b})$=$\{high-dimensional\}$,则$\left|l_a\right|=16$;
$l_b=S_b\setminus(S_a\cap{S_b})$=$\{high-dimension\}$,则$\left|l_b\right|=14$;
故$\max(\left|l_a\right|,\left|l_b\right|)=16$;又由编辑距离定义,得$d(l_a,l_b)=2$; 故由公式(4),得${S}$$_{ns}=1-(2/16)=7/8$;
④由公式(1),得\ $S(S_a,S_b)=6/8+2/8*7/8=0.96875$.
计算完毕.
进一步分析可知,本文定义的具有字符串属性的两个对象相似性公式中,完全相同元素比例就是二者的 Jaccard 系数. 与传统方法直接使用Jaccard 系数作为两个字符串的相似性不同,定义3 将Jaccard 系数作为相同元素比例系数,由于 Jaccard 系数取值范围是$[0,1]$,因而将1 减去Jaccard 系数的部分作为不完全相同元素比例系数,然后将其 与改进的编辑距离相似性的乘积来度量相同的元素存在相似性的可能性. 这种度量不但考虑了两个字符串的完全相同 部分,还考虑了词语拼写错误而造成的影响,计算了不完全相同元素部分的相似性,因而较传统编辑距离更能 有效度量两个字符串之间的相似性. 因此,示例1 计算得到的相似性计算结果符合实际情况.
定义4 对象与对象集合的相似性度量 (similarity between object and object set) 假设 有一个对象${O}$ 和一个对象集合${OS}$,${OS}$ 包含若干对象$O_i$, 定义对象与对象集合相似性${S}$(${O}$,${OS}$) 为此对象与对象集合内所有对象的相似性的平均值,公式如下:
| \begin{equation} S(O,OS)=\frac{\sum_{i=1,O_i\in OS}^{|OS|} S(O,O_i)}{\left|OS\right|} \end{equation} | (4) |
考虑一种常见的异质网络聚类方法,联合聚类(co-clustering), 同时对数据对象和对象属性进行聚类. 联合聚类又称为 协同聚类或二部聚类(bi-clustering), 在文本挖掘[15]、基因表达分析[16]、图像检索[17]、推荐系统[18]等 领域具有广泛应用. 联合聚类认为,当使用矩阵方式表达数据时, 如果行和列具有相关性,则从任意一个维度进行单独聚类都会忽 略另一个维度的相关信息,因此应该从行和列两个角度同时进行聚类. 两种对象的原始数据一般包含三种信息,即决定对象属性 信息、辅助对象属性信息以及决定对象和辅助对象的关系信息, 并且决定对象对实体解析过程中起决定性作用.
综上,本文提出如下基于联合聚类思想的协同实体解析算法框架(图 1), 包括两阶段: 第一阶段根据决定对象的属 性对决定对象进行聚类, 同时根据决定对象和辅助对象的关系以及辅助对象属性信息确定辅助对象的关系信息; 第 二阶段根据辅助对象的属性和辅助对象的关系对辅助对象进行聚类.
 |
| 图 1 基于联合聚类思想的协同实体解析算法框架 |
输入 包含两种对象、规模为${n}$ 的数据集${D}$; 决定对象相似性阈值$\alpha$; 辅 助对象相似性阈值$\beta$;
输出 决定对象聚类结果和辅助对象聚类结果.
基于联合聚类的两种对象实体解析算法(two type entity resolution,TTER) 主要步骤如下(图 2).
 |
| 图 2 TTER算法伪代码 |
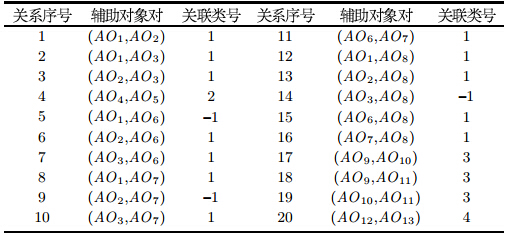
第一阶段,依次针对数据集中出现的决定对象和辅助对象, 判断决定对象的类归属情况,同时计算辅助对象之间的关系. 将第一个决定 对象作为第一个决定对象类、第一个辅助对象加入第一个决定对象类的辅助对象集合, 从第二个决定对象开始,根据定义4,依次计算 待分配决定对象与已有决定对象类的相似性: 若均小于决定对象相似性阈值$\alpha$,则将待分配决定对象作为一个新 的决定对象类,再将同时出现的辅助对象作为该类的辅助对象集合; 否则, 将待分配决定对象加入与其相似性最大 的已有决定对象类中, 将同时出现的辅助对象加入该决定对象类的辅助对象集合,然后根据定义3 计算的相似性,判断 该辅助对象与该类已有各辅助对象之间的关系: 若均小于辅助对象相似性阈值$\beta$,则用该类号标记该辅助对象与 各已有辅助对象的关系; 否则,用-1 标记该辅助对象与其相似性最大的辅助对象的关系, 用该类号标记与其他辅助对象的关系.
第二阶段,依次针对数据集中出现的辅助对象进行类分配. 将第一个辅助对象作为第一个辅助对象类,从第二个辅助 对象开始, 根据定义4,依次计算待分配辅助对象与已有辅助对象类的相似性: 若均小于$\beta$,则将待分配辅 助对象作为一个新的辅助对象类; 若满足$\beta$ 的辅助对象类个数为1,则将待分配辅助对象直接加入该类; 否则,将待 分配辅助对象加入满足$\beta$ 并且与其具有最多关系个数的辅助对象类中,若均不存在关系,则将待分 配辅助对象加入使得相似性最大的那个类. 2.3 算法时间复杂度分析
算法的运行时间主要由两部分组成, 第一部分是决定对象聚类和辅助对象关系的计算时间, 第二部分是辅助对象聚类的计算时间.
其中,第一部分扫描一条记录时, 通过判断决定对象与已有决定对象类的相似性来进行聚类, 并且同时计算辅助对象之间的关系,这部分计算的时间复杂度为$O(an)$, 其中$a$为决定对象类的个数,$n$为数据集大小; 第 二部分通过扫描数据集依次包含的辅助对象列表来对辅助对象进行聚类, 通过判断辅助对象与已有辅助对象类 的相似性来进行聚类, 这部分计算的时间复杂度为$O(bn)$,其中$b$为辅助对象类的个数.
因此,本文算法的时间复杂度为$O((a+b)n)$,其中,$a$ 为决定对象类的个数,$b$为辅助对象类的个数,$n$为数据规模, 一般来讲,$a<<n$,$b<<n$,$a+b<n$,时间复杂度小于朴素 关系型实体解析算法的二阶时间复杂度. 3 算法实验及结果分析 3.1 实验数据
由于目前鲜见对具有多种对象的实体解析问题的研究, 尚未有公认的数据集,因此,根据本文研究对象的特点和假设条件,构建 包含作者和文章两种对象的小规模文献数据作为实验数据, 其中每一条记录由一个作者实体参考表示和一个文章实体参考表示构成(表 1).
如前所述,实体解析可以帮助精简原始数据. 为了清晰比较应用实体解析算法前后数据集的变化,首先根据文章名称对此 数据集进行初步分析(图 3),得知在未进行实体解析之前数据集中存在5 篇不同名称的文章,涉及13 个作者,共有13 条文章和作者关系.
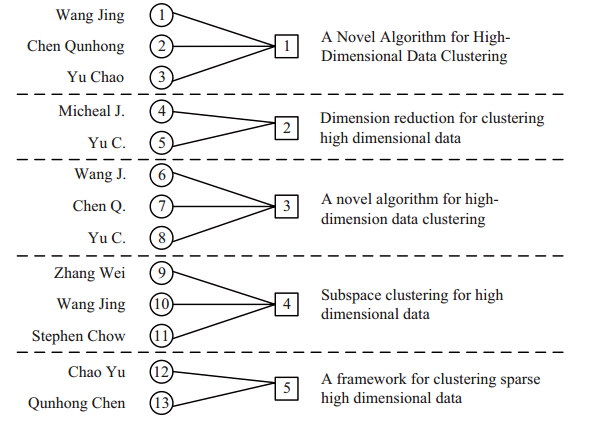 |
| 图 3 包含作者实体和文章实体的原始文献数据 |
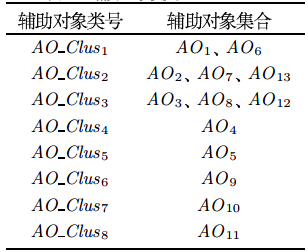
根据算法原理及步骤,设计算法的主要数据结构如下, 即决定对象类${DO\_Clus}$(表 2)、辅助对象关系 ${AO\_Relation}$ (表 3)和辅助对象类${AO\_Clus}$(表 4), 并填入上述数据的计算结果 ($\alpha=0.8$,$\beta=0.4$).
由表 2和表 4 获得经过本文算法实体解析后的结果(图 4),可知将决定对象分为4 类, 表明此文献数据集中包含4 篇文章,原始数据中具有不同名称的第1 篇文章(对应于 ${DO}$$_1$、${DO}$$_2$ 和${DO}$$_3$) 和第3 篇文章 (对应于${DO}$$_6$、${DO}$$_7$ 和${DO}$$_8$) 实际上指向同一篇文章; 同时将辅助对象分为8 类, 表明此文献数据集中包含8 个作者,原始数据中的第1 和第6 作者实际上指向现实世界中同一个作者,第2、第7 和第13 作者指向同一个作者,第3、第8 和第12 作者也指向同一个作者,并且有2 个Wang Jing (对应于 sloppy{${AO\_Clus}$$_1$ 和 ${AO\_Clus}$$_7$)、2 个Yu C. (对应于${AO\_Clus}$$_3$ 和 ${AO\_Clus}$$_5$).
进一步比较可知,实体解析后的数据更为精简(图 4),仅包含4 个文章、8 个作者、10 条关系,Wang Jing、Chen Qunhong和Yu Chao合作多, 说明实体解析可以起到清洗数据和初步发现对象之间潜在关系的作用. 此外,为了测试算法效率,还将上述实验数据复制多次分别得到100条、1000 条和10000 条三种规模实验数据,测试算法运行时间. 实验环境: 操作系统为CentOS 6.4、CPU为Intel Core 3.40 GHz、内存为10 GB、编程语言为Java. 测试得算法在100 条、1000 条、10000 条数据上各自运行5 次的平均时间分别为0.1086 秒、2.8180 秒、320.9822 秒,说明算法能够在较短时间内处理万级规模数据.
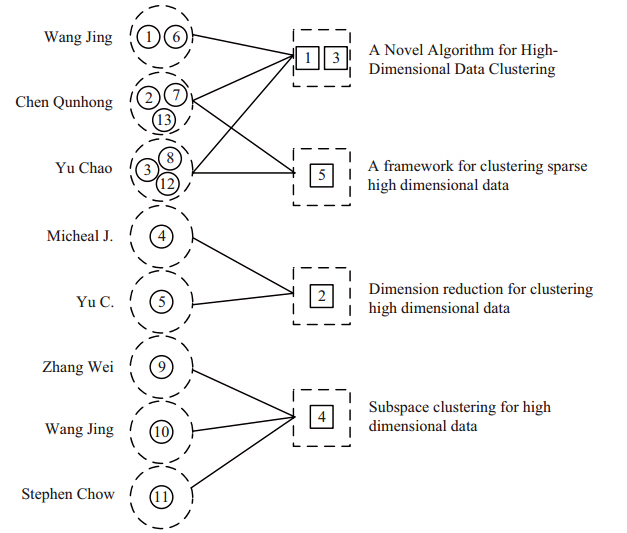 |
| 图 4 包含作者实体和文章实体的文献数据实体解析之后 |
本文针对具有两种对象的实体解析问题, 为了充分利用决定对象和辅助对象的属性信息以及二者之间的关 系信息, 采用联合聚类的思想,同时对两种对象进行聚类, 聚类结果中划分到同一类的对象指向现实世界中 的同一个实体. 研究中提出的根据字符串属性计算对象之间相似性的方法,弥补了Jaccard 系数未考虑两个字符串不完全相同的元素存在相似性的可能性和传统编辑距离仅反映两个字符串绝对差异的缺陷. 提出的基于联合聚类思想的两阶段协同实体解析通用框架, 可以同时对不同对象进行聚类,兼顾了实体解析准确度和算法时间复杂度. 算法通过一次顺序扫描完成对两种对象的聚类, 在对决定对象进行聚类的同时获得辅助对象之间的关系信息, 因而运行效率较传统实体解析算法有所提高. 实验结果表明两阶段协同实体解析方法能够有效识别数据集中的实体及实体之间的关系. 本文算法作为一种探索性算法, 下一步研究将通过算法在大规模数据上的性能分析, 完善算法步骤及提高算法效率,同时也考虑在实体解析结果基础上, 对两种对象进行聚类分析及聚类演化分析.
| [1] | Bhattacharya I, Getoor L. Collective entity resolution in relational data[J]. ACM Transactions on Knowledge Discovery from Data, 2007, 1(1): 1-36. |
| [2] | 楼俊杰, 徐从富, 郝春亮. 基于马尔可夫逻辑网络的实体解析改进算法[J]. 计算机科学, 2010, 37(8): 243-247. Lou Junjie, Xu Congfu, Hao Chunliang. Improvement of entity resolution based on Markov logic networks[J]. Computer Science, 2010, 37(8): 243-247. |
| [3] | Yu P S, Han J W, Faloutsos C. Link mining: Models, algorithms, and applications[M]. New York: Springer-Verlag, 2010: 118-119. |
| [4] | Getoor L. Link mining: A new data mining challenge[J]. ACM SIGKDD Explorations Newsletter, 2003, 5(1): 84-89. |
| [5] | Jaccard P. Étude comparative de la distribution florale dans une portion des alpes et des jura[J]. Bulletin del la Société Vaudoise des Sciences Naturelles, 1901, 37(142): 547-579. |
| [6] | Jaro M A. Probabilistic linkage of large public health data files[J]. Statistics in Medicine, 1995, 14(5-7): 491-498. |
| [7] | Winkler W E. The state of record linkage and current research problems[R]. Technical Report, Statistical Research Division, U.S. Census Bureau, 1999. |
| [8] | Levenshtein V I. Binary codes capable of correcting deletions, insertions and reversals[J]. Soviet Physics-Doklady, 1966, 10(8): 707-710. |
| [9] | Monge A E, Elkan C P. The field matching problem: Algorithms and applications[C]// Proceedings of the Second ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York: ACM Press, 1996: 267-270. |
| [10] | Ananthakrishna R, Chaudhuri S, Ganti V. Eliminating fuzzy duplicates in data warehouses[C]// Proceedings of the 28th International Conference on Very Large Databases, Massachusetts: Morgan Kaufmann Publishers, 2002: 586-597. |
| [11] | Kalashnikov D V, Mehrotra S, Chen Z Q. Exploiting relationships for domain-independent data cleaning[C]// Proceedings of the Fifth SIAM International Conference on Data Mining, Philadelphia: Society for Industrial and Applied Mathematics, 2005: 262-273. |
| [12] | Bhattacharya I, Getoor L. A latent Dirichlet model for unsupervised entity resolution[C]// Proceedings of the Sixth SIAM Conference on Data Mining, Philadelphia: Society for Industrial and Applied Mathematics, 2006: 47-58. |
| [13] | 刁兴春, 谭明超, 曹建军. 一种融合多种编辑距离的字符串相似度计算方法[J]. 计算机应用研究, 2010, 27(12): 4523-4525.Diao Xingchun, Tan Mingchao, Cao Jianjun. New method of character string similarity compute based on fusing multiple edit distances[J]. Application Research of Computers, 2010, 27(12): 4523-4525. |
| [14] | 黄林晟, 邓志鸿, 唐世渭, 等. 基于编辑距离的中文组织机构名简称-全称匹配算法[J]. 山东大学学报(理学版), 2012, 47(5): 43-48.Huang Linsheng, Deng Zhihong, Tang Shiwei, et al. A Chinese organization's full name and matching abbreviation algorithm based on edit-distance[J]. Journal of Shandong University (Natural Science), 2012, 47(5): 43-48. |
| [15] | Dhillon I S. Co-clustering documents and words using bipartite spectral graph partitioning[C]// Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York: ACM Press, 2001: 269-274. |
| [16] | Cho H, Dhillon I S, Guan Y Q, et al. Minimum sum-squared residue co-clustering of gene expression data[C]// Proceedings of the Fourth SIAM International Conference on Data Mining, Philadelphia: Society for Industrial and Applied Mathematics, 2004: 114-125. |
| [17] | Qiu G P. Image and feature co-clustering[C]// Proceedings of the 17th IEEE International Conference on Pattern Recognition, New York:IEEE Press, 2004: 991-994. |
| [18] | 吴湖, 王永吉, 王哲, 等. 两阶段联合聚类协同过滤算法[J]. 软件学报, 2010, 21(5): 1042-1054.Wu Hu, Wang Yongji, Wang Zhe, et al. Two-phase collaborative filtering algorithm based on co-clustering[J]. Journal of Software, 2010, 21(5): 1042-1054. |