0 引言
客观世界的实际问题往往涉及众多相互联系又相互影响的因素, 这些因素本身及其相互之间的关系都存在大量的不确定性, 而不确定性可分为两类, 一类是反映客观事物内在本质的随机不确定性(aleatory uncertainty), 一类是反映由于人们对客观世界的认识不足、信息缺失或知识缺乏而导致的认知不确定性(epistemic uncertainty)[1]. 如何描述各种不确定性, 如何在复杂关系分析中对问题有效地建模, 如何综合定量数据和定性知识而做出科学的决策, 都对不确定性决策问题的研究提出了新的挑战.
为解决不确定性与关联性并存的管理决策问题,将D-S 证据理论与图模型相结合,借鉴贝叶斯网络的研究思路,建 立证据网络模型.证据网络将综合图模型在问题描述、关系分析上的语义优势,及D-S 证据理论在不确定性信息处理,尤其是认知 不确定性的建模和分析上的理论优势,为不确定性决策问题的分析、建模、推理以及评估、决策提供技术方法与工具支撑.
证据网络的研究目前还处于萌芽阶段, 其建模、推理及应用方面的研究还很少, Xu等最早采用条件信度函数来表示网络结点之间的关系, 提出了带条件信度函数的信度网络概念[2]. Yaghlane等人通过对比分析证据网络与VBS的异同,指出证据网络研究的主要问题就是用有向无环图加信度函数的形式,表示网 络中的知识和条件关系,通过DRC和GBT实现EN的推理[3]. Simon等 连续发表几篇文章,把贝叶斯网络和证据理论相结合,用来解决复杂系统可靠性问题,主要扩展处理带有不完全、 不精确信息的可靠性问题,推理模式还是用的贝叶斯理论[4, 5, 6]. 此外,证据网络在信息融合、智能控制、威胁评估、医疗护理、侦查探测等应用中[7, 8, 9] 也做出了初步尝试.国内目前关于证据网络理论与方法的研究还很少,王晓媛采用D-S 证据理论和贝叶斯网络相结合的证据网络推理解决了SDH 设备可靠性分析中的不确定性、不完备性等问题[10]. 本文作者详细梳理与综述了不确定性的分类、不确定性处理方法、不确定性推理方法的研究现状与优缺点,对证据理论的研 究现状进行了分类整理和分析,总结了研究中存在的问题,研究了证据网络模型的建模方法[11], 并将证据网络模型应用于航天系统安全性分析中,解决航天系统安全性分析与评价中面临的不精确、不完全信息难以处 理等问题,总结了证据网络在风险安全性分析与评估中的操作流程与步骤[12, 13].
本文在D-S证据理论及推理的研究基础上,给出证据网络模型的基本定义,建立其参数模型,总结证据网络模型的特点; 然后围绕证据网络推理策略与算法展开论述,规范其推理问题,提出推理策略,推导证据网络推理的正向推理算法和反向推 理算法,并给出计算示例. 1 证据网络模型 1.1 证据网络模型的概念
证据网络(evidential network,EN)是一种有向无环图(directed acyclic graph,DAG)模型,由代表变量的结点和连接这些结点的有向边、以及相应的关系参数构成,是图论与证据理论的结合. 形式化表示为$EN=\{(N,A),B\}$,$N$ 为结点的集合, $A$为结点间连接弧的集合, $(N,A)$即为一个具有$N$个结点的有向无环图$G$; $B$为结点之间的信度函数关系集合,其编码了一组变量之间的相互关系.证据网络主要由两部分构成: 网络结构与网络参数,一个基本的证据网络如图 1. 证据网络的结构是一个有向无环图,由结点集$N$和有向边集$A$ 构成,证据网络的参数$B$ 反映结点之间的关联程度或影响程度.
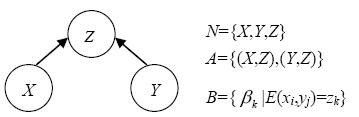 |
| 图 1 基本的证据网络模型 |
条件信度函数(conditional belief function, CBF)是D-S证据理论中的``贝叶斯函数",其功能类似于贝叶斯网络中条件概率函数.所以,利用条件信度函数作为证 据网络的参数模型,是一种有效的知识描述方式,可以定量化地表征网络结点之间的关联程度.根据D-S证据理论的基本 概念及其相关定义[14, 15],给出证据网络模型参数$B$的表达方式.
定义1 某命题的各种相互独立的可能方案构成一个有限集合$\Theta =\left\{ {{\theta }_{1}},{{\theta }_{2}},\cdots,{{\theta }_{N}} \right\}$, 称$\Theta $ 为该命题的一个识别框架(frame of discernment). $\Theta $ 中所有可能集合用幂集合${{2}^{\Theta }}$ 来表示,当$\Theta $中的元素有$N$ 个,则$\Theta $的幂集合${{2}^{\Theta }}$ 的元素个数为${{2}^{N}}$.
定义2 设$\Theta $为识别框架,如果存在函数$m:{{2}^{\Theta }}\to [0,1]$,满足:
$m(X)\ge 0,$ $\sum\limits_{X\subseteq \Theta }{m(X)=1}.$
则称函数$m$为$\Theta $上的基本信度分配(basic belief assignment).
定义3 设有限非空集$\Theta $为识别框架,函数$m:{{2}^{\Theta }}\to [0,1]$为框架$\Theta $ 上的基本信度分配,则函数$Bel:{{2}^{\Theta }}\to [0,1]$定义为$\Theta $ 上的信度函数(belief function),满足:
$Bel(\emptyset )=0$,$Bel(X)=\sum\limits_{Y\subseteq X,Y\ne \emptyset }{m(Y)},\forall X,Y\subseteq \Theta .$
式中$Bel(X)$反映所有$X$的子集的精确信度总和.
定义4 设有限非空集$\Theta $为识别框架,函数$m:{{2}^{\Theta }}\to [0,1]$为框架$\Theta $ 上的基本信度分配,则函数$Pl:{{2}^{\Theta }}\to [0,1]$ 定义为$\Theta $ 上的似然函数(plausibility function),满足:
(a) $Pl(\emptyset )=0,$ (b) $Pl(X)=\sum\limits_{X\cap Y\ne \emptyset }{m(Y)},\forall X,Y\subseteq \Theta .$
定义5 设有限非空集$\Theta $为识别框架,函数$m:{{2}^{\Theta }}\to [0,1]$为框架$\Theta $ 上的基本信度分配,函数$Bel:{{2}^{\Theta }}\to [0,1]$ 为框架$\Theta $ 上的信度函数,则函数$b:{{2}^{\Theta }}\to [0,1]$ 定义为$\Theta $ 上的蕴涵信度函数(implicability function),满足:
$b(X)=Bel(X)+m(\emptyset ),\forall X\subseteq \Theta $.
定义6 设$\Theta $是识别框架,$m$是$\Theta $ 上的基本信度分配,对$A,B\subseteq \Theta $,条件基本可信度定义为, $$m\left( B|A \right)=\left\{ \begin{matrix} \sum\limits_{X\subseteq \bar{A}}{m(B\bigcup X)},& B\subseteq A\subseteq \Theta \\ 0,& \mbox{others} \\ \end{matrix} \right..$$
定义7 设$\Theta $是识别框架,$Bel$是$\Theta $ 上的信度函数,对$A,B\subseteq \Theta $,$\Theta $ 上的条件信度函数定义为,
$Bel\left( B|A \right)=Bel(B\bigcup \bar{A})-Bel(\bar{A}),\begin{matrix} {} & \forall B\subseteq \Theta . \\ \end{matrix}$
$Be{{l}_{{}}}(B|A)$意为在给定$A$的情况下,$B$的信度.
定义8 设$\Theta $是识别框架,$Pl$是$\Theta $上的似然函数,对$A,B\subseteq \Theta $,$\Theta $ 上的条件似然函数定义为,
$Pl\left( B|A \right)=Pl(A\bigcap B),\begin{matrix} {} & \forall B\subseteq \Theta . \\ \end{matrix}$
定义9 设$\Theta $是识别框架,$q$是$\Theta $ 上的众信度函数,对$A,B\subseteq \Theta $,$\Theta $ 上的条件众信度函数定义为, $$q\left( B|A \right)=\left\{ \begin{matrix} q(B),& B\subseteq A \\ 0,& \mbox{others} \\ \end{matrix} \right..$$
定义10 设$\Theta $是识别框架,$b$是$\Theta $上的蕴涵信度函数,对$A,B\subseteq \Theta $,$\Theta $ 上的条件蕴涵信度函数定义为,
$b\left( B|A \right)=b(B\bigcup \bar{A}),\begin{matrix} {} & \forall B\subseteq \Theta . \\ \end{matrix}$
由D-S证据理论的基础知识可知,基本信度分配、信度(似然度、众信度)函数之间可以建立一一对应关系[14], 同样,其条件信度函数之间也存在相关性,可以通过算法相互转化.以下定理给出条件基本可信度、条件信度、条件似然函数 之间的相互关系.
定理1 设$X$和$Y$的识别框架分别为${{\Theta }_{X}}$ 和${{\Theta }_{Y}}$,$x\subseteq {{\Theta }_{X}}$, 对任意$\emptyset \ne y\subseteq {{\Theta }_{Y}}$,给定$x$情况下$y$ 的条件信度函数为,
$Bel(y|x)=\sum\limits_{z\subseteq {{\Theta }_{Y}},z\subseteq y}{m(z|x)}.$
定理2 设$X$和$Y$的识别框架分别为${{\Theta }_{X}}$ 和${{\Theta }_{Y}}$,$x\subseteq {{\Theta }_{X}}$,对任意$\emptyset \ne y\subseteq {{\Theta }_{Y}}$,给定$x$情况下$y$ 的条件似然函数为,
$Pl(y|x)=\sum\limits_{z\subseteq {{\Theta }_{Y}},z\bigcap y\ne \emptyset }{m(z|x)}.$
定理3 条件基本信度分配,条件信度函数与条件似然函数还存在以下关系,
$Bel(y|x)=1-Pl(\bar{y}|x),$ $m(y|x)=\sum\limits_{z\subseteq y}{{{(-1)}^{|y-z|}}Bel(z|x)}.$
1.3 证据网络模型的特点证据网络作为一种图模型,具有图模型的大多数性质,图模型和图论方法为证据网络提供了直观的问题描述方式,使 得对问题变量之间的相互关系易于理解,证据网络的特点主要体现在:
■ 证据网络本身是一种不确定性因果关联模型,是将多元知识图解可视化的一种信度知识表达与推理模型,更为贴切地蕴 涵了网络结点变量之间的因果及相互关系.
■ 证据网络模型符合人们处理复杂问题的自然思维模式,其模型建立和知识表示容易理解,语义清晰,将高度互动化 的变量集和数据结构模型化.
■ 证据网络可有效克服不确定性建模中面临的问题,充分发挥证据理论处理认知不确定性信息的能力,尤其是当信 息不完全、不精确甚至无知情况下的推理问题.
■ 证据推理方法为证据网络的运算和传播提供了坚实的数学理论基础,使得证据网络不但具有推理能力,还具有 预测、诊断等功能,可实现多源异类不确定性信息条件下的知识处理.
■ 证据网络模型通过网络参数的影响模式分析和赋值,把对复杂问题的分析和经验知识信息有机的结合在一起,并可进 行局部模块化处理,减低了对复杂问题求解的难度.
■ 证据网络具有因果和信度语义,可以利于专家知识和观测数据对网络中的因果关系和参数进行学习,特别是可以跟优化 和决策方法相结合.
■ 证据网络可以与其他相关理论技术相结合,增强了证据网络的稳健性和可扩展性.
■ 证据网络具有规范的建模方法和推理算法,利于在计算机上程序实现,可为处理大型复杂问题提供有效的工具.\vspace{-2mm} 2 证据网络推理策略及算法
证据网络的推理就是当获得某些网络结点的观察信息后,估计未知结点的状态,理论上就是进行信度计算; 具体而言,就是在已知网络结构模型和参数模型的情况下,通过信度推理算法求得感兴趣结点的信度值. 2.1 证据网络模型的推理问题
证据网络模型的推理就是对真实系统通过证据网络结构模型识别关键变量或要素,并建立它们之间的相互关系,通过信 度规则参数模型描述它们之间的影响程度,然后根据系统某变量的状态信息,推断其他结点的状态信息.
在理论上,以条件信度函数为参数模型的证据网络推理,就是要通过严格的数学推导算法,实现信息在证据网络中的有效传播, 由于条件信度函数是根据网络有向弧的方向表示的从原因到结果的关系信息,其推理形式主要包括两类:
1)因果推理,即由原因推知结论,又称前向推理或正向推理.在证据网络模型建立后,已知叶结点的状态信息(证据),使用证据 网络推理算法,计算求得在该种场景下,中间结点与顶结点的状态信度.
2)诊断推理,即由后果推知原因,又称后向推理或反向推理.在证据网络模型建立后,已知顶结点或中间结点的状态信息(证据), 使用证据网络推理算法,计算求得在该种场景下,其他感兴趣的结点的状态信度. 2.2 证据网络推理策略
证据网络推理在思路上借鉴贝叶斯网络推理的研究,其推理过程同样包括三个主要步骤: 1)信度初始化,即每个结点根据现有信息对信度进行赋值; 2)信息传递,即计算结点之间的信息传递,包括来自父结点的信度值和来自子结点的信度值; 3)结点信息更新,根据结点初始值和相互间信息传递值,计算每个结点更新后的信度值.
如图 2所示的证据网络模型,假设网络结构和条件信度已知,即此证据网络的结点集合为$N=\{P,X,Y,Z\}$, 有向弧 集合为$A=\{(P,Y),(Y,X),(Z,X)\}$,参数模型为$Bel(y|p)$, $Bel(x|y)$,$Bel(x|z)$,这里假设$X,Y,Z,P$ 的识别框架为${{\Theta }_{X}},{{\Theta }_{Y}},{{\Theta }_{Z}},{{\Theta }_{P}}$,$x\in {{\Theta }_{X}},y\in {{\Theta }_{Y}},z\in {{\Theta }_{Z}},p\in {{\Theta }_{P}}$.
 |
| 图 2 证据网络推理 |
1)因果推理的求解策略
假设已知$Y$的取值为${{y}_{0}}\in {{\Theta }_{Y}}$, $Z$的取值为${{z}_{0}}\in {{\Theta }_{Z}}$,那么$X$ 的状态信息可以由${{y}_{0}}$,${{z}_{0}}$以及它们与$X$ 之间的条件信度$Bel(x|y)$ 和$Bel(x|z)$得到,即$Be{{l}_{X}}(x)$ 可看作${{y}_{0}}$,${{z}_{0}}$,$Bel(x|y)$ 和$Bel(x|z)$ 的函数$F$:
$Be{{l}_{X}}(x)=F\left( {{y}_{0}},{{z}_{0}},Bel(x|y),Bel(x|z) \right).$
函数$F$的求解包括以下几步:
\textcircled{\small 1}信息转化: 将$Y$和$Z$的取值${{y}_{0}}$, ${{z}_{0}}$ 转换到证据理论的信度表示框架下;
\textcircled{\small 2}正向推理: 即由${{y}_{0}}$与$Bel(x|y)$计算$Be{{l}_{X}}(x)\left| {{y}_{0}} \right.$,由${{z}_{0}}$ 与$Bel(x|z)$计算$Be{{l}_{X}}(x)\left| {{z}_{0}} \right.$;
\textcircled{\small 3}信度合成: 将$Be{{l}_{X}}(x)\left| {{y}_{0}} \right.$ 与$Be{{l}_{X}}(x)\left| {{z}_{0}} \right.$ 进行合成,得到$X$的推理结果.
2)诊断推理的求解策略
假设已知$X$的取值为${{x}_{0}}\in {{\Theta }_{X}}$, $P$的取值为${{p}_{0}}\in {{\Theta }_{P}}$,那么$Y$ 的状态信息可以由${{x}_{0}}$,${{p}_{0}}$以及它们与$Y$ 之间的条件信度$Bel(x|y)$ 和$Bel(y|p)$得到,即$Be{{l}_{Y}}(y)$ 可看作${{x}_{0}}$,${{p}_{0}}$,$Bel(x|y)$ 和$Bel(y|p)$ 的函数$G$:
$Be{{l}_{Y}}(y)=G\left( {{x}_{0}},{{p}_{0}},Bel(x|y),Bel(y|p) \right).$
函数$G$的求解包括以下几步:
\textcircled{\small 1}信息转化: 将$X$和$P$的取值${{x}_{0}}$, ${{p}_{0}}$ 转换到证据理论的信度表示框架下;
\textcircled{\small 2}正向推理: 即由${{p}_{0}}$与$Bel(y|p)$计算$Be{{l}_{Y}}(y)\left| {{p}_{0}} \right.$;
\textcircled{\small 3}反向推理: 即由${{x}_{0}}$与$Bel(x|y)$计算$Be{{l}_{Y}}(y)\left| {{x}_{0}} \right.$;
\textcircled{\small 4}信度合成: 将$Be{{l}_{Y}}(y)\left| {{p}_{0}} \right.$ 与$Be{{l}_{Y}}(y)\left| {{x}_{0}} \right.$ 进行合成,得到$Y$的推理结果.
信息转化可以通过D-S证据理论中信度表示之间的相互关系进行计算[14],以下在条件信度函数计 算基本理论的基础上,研究给出正向推理和反向推理算法. 2.3 证据网络推理算法
从条件信度函数的基本定义定理出发,可以得到从基本信度表示计算条件信度函数的简单算法; 然后,在条件信度计算规则的基础上建立证据网络条件信度正向和反向推理算法. 2.3.1 证据网络正向推理算法
如图 2所示的证据网络模型,假设结点$X,Y$的识别框架为${{\Theta }_{X}}$ 和${{\Theta }_{Y}}$ (简记为$X$和$Y$),对$\forall y\subseteq Y,\forall x\subseteq X,$ 根据条件基本可信度的定义5, 条件信度函数计算定理以及扩展和边际化运算定理[14, 15], 得到$Y$到$X$的条件基本可信度函数为, \begin{equation} {{m}_{X}}\left( x|y \right)=\sum\limits_{\left( \bigcup\nolimits_{i:{{y}_{i}}\in y}{{{x}_{i}}} \right)=x} {\prod\limits_{i:{{y}_{i}}\in y}{{{m}_{X}}({{x}_{i}}|{{y}_{i}})}}(1) \end{equation}
由D-S证据理论的基础知识可知,其条件信度函数之间存在相关性,可以通过定理1$\sim$定理3 进行相互转换.因此,公式(1) 可以表示为条件蕴涵信度函数的形式为, \begin{equation} {{b}_{X}}\left( x|y \right)=\prod\limits_{{{y}_{i}}\in y}{{{b}_{X}}\left( x|{{y}_{i}} \right)}(2) \end{equation}
同理,以条件信度函数和条件似然函数的形式可以表示为, \begin{equation} Be{{l}_{X}}\left( x|y \right)={{b}_{X}}\left( x|y \right)-{{b}_{X}}\left( \emptyset |y \right)(3) \end{equation} \begin{equation} P{{l}_{X}}\left( x|y \right)=1-\prod\limits_{{{y}_{i}}\in y}{\left( 1-P{{l}_{X}}(x|{{y}_{i}}) \right)}(4) \end{equation}
进一步,如果已知$Y$各个状态或子集上的信度信息,记为${{m}_{0}}(y),y\subseteq Y$,那么对$\forall x\subseteq X$,有, \begin{equation} {{m}_{X}}(x)=\sum\limits_{y\subseteq Y}{{{m}_{0}}(y){{m}_{X}}(x|y)}(5) \end{equation}
公式(5)以条件基本可信度表示,同理根据公式(3)和(4),用条件信度和条件似然函数表示为, \begin{equation} Be{{l}_{X}}(x)=\sum\limits_{y\subseteq Y}{{{m}_{0}}(y)Be{{l}_{X}}(x|y)}=\sum\limits_{y\subseteq Y} {{{m}_{0}}(y)}\left( \prod\limits_{{{y}_{i}}\in y}{{{b}_{X}}(x|{{y}_{i}})}-\prod\limits_{{{y}_{i}} \in y}{{{b}_{X}}(\emptyset |{{y}_{i}})} \right)(6) \end{equation} \begin{equation} P{{l}_{X}}(x)=\sum\limits_{y\subseteq Y}{{{m}_{0}}(y)P{{l}_{X}}(x|y)}=\sum\limits_{y\subseteq Y}{{{m}_{0}} (y)\left( 1-\prod\limits_{{{y}_{i}}\in y}{(1-P{{l}_{X}}(x|{{y}_{i}}))} \right)}(7) \end{equation} 2.3.2 证据网络反向推理算法
如图 2所示的证据网络模型,假设结点$X,Y$的识别框架为${{\Theta }_{X}}$ 和${{\Theta }_{Y}}$ (简记为$X$和$Y$),对$\forall y\subseteq Y,\forall x\subseteq X,$ 如果可以由$Y$到$X$的条件信度函数$Bel(x|y)$ 得到$X$到$Y$ 的条件信度函数$Bel(y|x)$,即可实现证据网络条件信度的反向推理.
首先,根据蕴涵信度函数的定义,结合扩展和边际化运算定理,得到条件蕴涵信度函数的反向转化公式, \begin{equation} {{b}_{Y}}\left( y|x \right)=\prod\limits_{{{y}_{i}}\in \bar{y}}{{{b}_{X}}(\bar{x}|{{y}_{i}})}(8) \end{equation}
与正向推理的研究思路一致,条件信度、似然、众信度函数之间存在对应关系,通过它们之间的关系定理1$\sim$定理3 及上节得到的正向推理算法(3) 与(4),得到对应的条件函数如下, \begin{equation} Be{{l}_{Y}}\left( y|x \right)={{b}_{Y}}\left( y|x \right)-{{b}_{Y}}\left( \emptyset |x \right)(9) \end{equation} \begin{equation} P{{l}_{Y}}\left( y|x \right)=1-\prod\limits_{{{y}_{i}}\in y}{\left( 1-P{{l}_{X}}\left( x|{{y}_{i}} \right) \right)}(10) \end{equation} \begin{equation} {{q}_{Y}}\left( y|x \right)=\prod\limits_{{{y}_{i}}\in y}{P{{l}_{X}}\left( x|{{y}_{i}} \right)}(11) \end{equation} 根据公式(4)和(10)可知, $$P{{l}_{X}}\left( x|y \right)=1-\prod\limits_{{{y}_{i}}\in y}{\left( 1-P{{l}_{X}}(x|{{y}_{i}}) \right)}=P{{l}_{Y}}\left( y|x \right).$$ 即得到 \begin{equation} P{{l}_{Y}}(y|x)=P{{l}_{X}}(x|y)(12) \end{equation}
公式(12)使得证据网络条件信度推理运算在计算上大大简化,公式(8)$\sim$(11) 给出了如何由$Y$ 到$X$的条件信度函数$Bel(x|y)$得到$X$到$Y$ 的条件信度函数$Bel(y|x)$,再根据公式(5)$\sim$(7) 的计算方法,即可得到证据网络的反向推理的计算方法.
此外,如果把条件信度函数$Be{{l}_{X}}(\cdot |{{y}_{i}})$ 看作$X$ 上的概率函数$P(\cdot |{{y}_{i}})$,即有$\left| y \right|=1$, 那么公式(10) 变为:
$P{{l}_{Y}}(y|x)=P(x|y),\begin{matrix} {} & \forall x\subseteq X. \\ \end{matrix}$
3 证据网络推理算例本小节通过一个简单的证据网络推理示例,演示验证上述条件信度参数模型下的证据网络推理算法的可行性.假定某 系统S是否正常运行可以通过测试T 来反映,为简单起见,设系统S只有两种状态\{`故障', `正常'\},表示为$\{F,N\}$,其识别框架定义为${{\Theta }_{S}}=\left\{ \emptyset ,\{F\},\{N\},\{F,N\} \right\}$; 测试结果也有两种情况\{`高', `低'\},表示为$\{H,L\}$,其识别框架定义为${{\Theta }_{T}}=\left\{\emptyset ,\{H\},\{L\},\{H,L\} \right\}$,其证据网络如图 3 所示.根据专家知识或历史信息,可以初步建立S到T 的条件信度$Be{{l}_{T}}(\cdot |s),s\subseteq S$, 假设已知条件基本可信度为,$$\begin{matrix} {{m}_{T}}(\{H\}|\{F\})=0.96,& {{m}_{T}}(\{H,L\}|\{F\})=0.04,\\ {{m}_{T}}(\{L\}|\{N\})=0.9,& {{m}_{T}}(\{H,L\}|\{N\})=0.1. \\ \end{matrix}$$
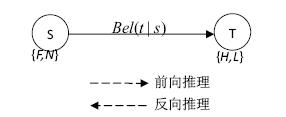 |
| 图 3 证据网络条件信度推理示例 |
示例1 假设经过测试,T的初步结果以基本可信度的形式表示为,
${{m}_{T}}(\{H\})=0.8,{{m}_{T}}(\{L\})=0.1,{{m}_{T}}(\{H,L\})=0.1.$
那么,根据测试T的信息,推理求解系统S的状态信度值.
此问题属于反向推理问题,首先,需要根据条件信度$Be{{l}_{T}}(\cdot |s)$求条件信度$Be{{l}_{S}}(\cdot |t)$, 因为已知信息以基本条件可信度表示,先利用定理1$\sim$定理2 将${{m}_{T}}(\cdot |s)$转为$P{{l}_{T}}(\cdot |s)$,
$P{{l}_{T}}(\{H\}|\{F\})=\sum\limits_{t\subseteq {{\Theta }_{T}},t\bigcap \{F\}\ne \emptyset }{{{m}_{T}}(t|\{F\})}={{m}_{T}}(\{H\}|\{F\})+{{m}_{T}}(\{H,L\}|\{F\})=1,$
同理,计算$P{{l}_{T}}(\{L\}|\{F\})=0.04,P{{l}_{T}}(\{H,L\}|\{F\})=1,$ $P{{l}_{T}}(\{H\}|\{N\})=0.1,P{{l}_{T}}(\{L\}|\{N\})=1,P{{l}_{T}}(\{H,L\}|\\ \{N\})=1.$
第二步,运用公式(10),公式(12),由$P{{l}_{T}}(\cdot |s)$ 计算$P{{l}_{S}}(\cdot |t)$ 得,
$P{{l}_{S}}\left( \{N\}|\{H\} \right)=1-\prod\limits_{{{s}_{i}}\in \{N\}}{\left( 1-P{{l}_{T}}\left( t|{{s}_{i}} \right) \right)}=1-\left( 1-P{{l}_{T}}(\{H\}|\{N\}) \right)=1-(1-0.1)=0.1$.
同理,$P{{l}_{S}}\left( \{F\}|\{H\} \right)=1,P{{l}_{S}}\left( \{F,N\}|\{H\} \right)=1,$ $P{{l}_{S}}\left( \{F\}|\{L\} \right)=1,P{{l}_{S}}\left( \{N\}|\{L\} \right)=0.96,P{{l}_{S}}\left( \{F,N\}|\{L\} \right)\\=1.$
第三步,利用条件信度之间的关系定理3,将$P{{l}_{S}}(\cdot |t)$ 转为$Be{{l}_{S}}(\cdot |t)$,再转为${{m}_{S}}(\cdot |t)$,
$Be{{l}_{S}}(\{F\}|\{H\})=1-P{{l}_{S}}(\{N\}|\{H\})=1-0.1=0.9,$
${{m}_{S}}(\{F\}|\{H\})=\sum\limits_{s\subseteq \{F\}}{{{(-1)}^{|\{F\}-s|}}Be{{l}_{S}}(s|\{H\})}=Be{{l}_{S}}(\{F\}|\{H\})=0.9,$
同理,$Be{{l}_{S}}(\{N\}|\{H\})=0,Be{{l}_{S}}(\{F,N\}|\{H\})=1,$
$Be{{l}_{S}}(\{F\}|\{L\})=0,Be{{l}_{S}}(\{N\}|\{L\})=0.96,Be{{l}_{S}}(\{F,N\}|\{L\})=1,$
$Be{{l}_{S}}(\{F\}|\{H,L\})=0,Be{{l}_{S}}(\{N\}|\{H,L\})=0,Be{{l}_{S}}(\{F,N\}|\{H,L\})=1.$
${{m}_{S}}(\{N\}|\{H\})=0,{{m}_{S}}(\{F,N\}|\{H\})=0.1,$
${{m}_{S}}(\{F\}|\{L\})=0,{{m}_{S}}(\{N\}|\{L\})=0.96,{{m}_{S}}(\{F,N\}|\{L\})=0.04,$
${{m}_{S}}(\{F\}|\{H,L\})=0,{{m}_{S}}(\{N\}|\{H,L\})=0,{{m}_{S}}(\{F,N\}|\{H,L\})=1.$
第四步,根据公式(5),在已知${{m}_{T}}(\{t\})$基础上,推理计算${{m}_{S}}(\{s\})$,
${{m}_{S}}(\{F\})=\sum\limits_{t\subseteq {{\Theta }_{T}}}{{{m}_{0}}(t){{m}_{S}}(\{F\}|\{t\})}=0.8\times 0.9+0.1\times 0+0.1\times 0=0.72,$
${{m}_{S}}(\{N\})=\sum\limits_{t\subseteq {{\Theta }_{T}}}{{{m}_{0}}(t){{m}_{S}}(\{N\}|\{t\})}=0.8\times 0+0.1\times 0.96+0.1\times 0=0.096,$
${{m}_{S}}(\{F,N\})=\sum\limits_{t\subseteq {{\Theta }_{T}}}{{{m}_{0}}(t){{m}_{S}}(\{F,N\}|\{t\})}=0.8\times 0.1+0.1\times 0.04+0.1\times 1=0.184.$
所以,由以上推理得到系统S的状态信度为${{m}_{S}}(\{F\},\{N\},\{F,N\})=(0.72,0.096,0.184).$
示例2 假设已知系统S的初步状态以基本可信度的形式表示为,
${{m}_{S}}({F})=0.7,{{m}_{S}}({N})=0.2,{{m}_{S}}({F,N})=0.1.$
那么,根据系统S的信息,推理求解测试T可能状态的信度值?
此问题属于正向推理问题,需要由${{m}_{S}}(\{s\})$ 和$Be{{l}_{T}}(\cdot |s)$ 求${{m}_{T}}(\{t\})$. 由公式(1), 公式(5),得
${{m}_{T}}(\{H\})=\sum\limits_{s\subseteq {{\Theta }_{S}}}{{{m}_{S}}(s){{m}_{S}}(\{H\}|\{s\})}=0.7\times 0.96+0.2\times 0+0.1\times 0=0.672,$
${{m}_{T}}(\{H\})=\sum\limits_{s\subseteq {{\Theta }_{S}}}{{{m}_{S}}(s){{m}_{S}}(\{H\}|\{s\})}=0.7\times 0+0.2\times 0.9+0.1\times 0=0.18,$
${{m}_{T}}(\{H\})=\sum\limits_{s\subseteq {{\Theta }_{S}}}{{{m}_{S}}(s){{m}_{S}}(\{H\}|\{s\})}=0.7\times 0.04+0.2\times 0.1+0.1\times 1=0.148.$
所以,推理得到测试T可能的状态信度为${{m}_{S}}(\{H\},\{L\},\{H,L\})=(0.672,0.18,0.148).$ 4 总结
在管理决策实践中,不确定性与关联性无处不在,在理论和方法上探索考虑系统关联性和信息不确定性环境下,如何建立反映系统真实情况的模型,如何对定性知识与定量数据信息进行统一建模和处理,如何通过严格的推理计算不断增强人们对系统的认知等问题,具有重要的科学意义与实际价值.
本文通过对国内外研究现状的分析和整理,借鉴贝叶斯网络的研究思路,提出了证据网络模型的概念,给出了证据网络模型的定义,参数表述模型; 分析了证据网络的推理问题,建立了推理策略和求解过程,通过对条件信度函数基本运算和基本定理的深入研究,提出了证据网络模型的正向推理算法和反向推理算法,并通过示例进行了计算验证.完成整个证据网络的推理过程还需要结点的信度合成,本文主要提出了推理算法,关于信度合成的方法将在其他文章中研究.
证据网络是D-S证据理论和图模型的结合,其结合图模型在问题描述、关系分析上的语义优势,及D-S 证据理论在不确定性信息处理,尤其是认知不确定性的建模和分析上的理论优势,为不确定性决策问题的分析、建模、推理以及评估、决策提供技术方法与工具支撑.
| [1] | Kiureghian A D, Ditlevsen O. Aleatory or epistemic? Does it matter?[J]. Structural Safety, 2009, 31(2): 105-112. |
| [2] | Xu H, Smets P. Reasoning in evidential networks with conditional belief functions[J]. International Journal of Approximate Reasoning, 1996, 14(2-3): 155-185. |
| [3] | Yaghlane B B, Mellouli K. Inference in directed evidential networks based on the transferable belief model[J]. International Journal of Approximate Reasoning, 2008, 48(2): 399-418. |
| [4] | Simon C, Weber P, Evsukoff A. Bayesian networks inference algorithm to implement Dempster Shafer theory in reliability analysis[J]. Reliability Engineering and System Safety, 2008, 93(7): 950-963. |
| [5] | Simon C, Weber P. Imprecise reliability by evidential networks[J]. Journal of Risk and Reliability, 2009, 223(2): 119-131. |
| [6] | Simon C, Weber P. Evidential networks for reliability analysis and performance evaluation of systems with imprecise knowledge[J]. IEEE Transactions on Reliability, 2009, 58(1): 69-87. |
| [7] | Benavoli A, Ristic B, Farina A, et al. An application of evidential networks to threat assessment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 620-639. |
| [8] | Lee H, Choi J S, Elmasri R. A static evidential network for context reasoning in home-based care[J]. IEEE Transactions on Systems, Man, and Cybernetics: Part A——Systems and Humans, 2010, 40(6): 1232-1243. |
| [9] | Pichona F, Dubois D, Denoeuxc T. Relevance and truthfulness in information correction and fusion[J]. International Journal of Approximate Reasoning, 2012, 53(2): 159-175. |
| [10] | 王晓媛,高会生,金鑫,等.基于证据网络推理的SDH设备可靠性分析[J]. 电力系统通信, 2010, 31(10): 25-29.Wang Xiaoyuan, Gao Huisheng, Jin Jin, et al. Reliability analysis of SDH based on evidential network[J]. Telecommunications for Electric Power System, 2010, 31(10): 25-29. |
| [11] | 姜江.证据网络建模、推理及学习方法研究[D]. 长沙:国防科技大学, 2011.Jiang Jiang. Modeling, reasoning and learning approach to evidential network[D]. Changsha: National University of Defense Technology, 2011. |
| [12] | 姜江,李璇,陈英武,等. 证据网络及其在航天系统安全性分析中的应用[J]. 系统工程与电子技术, 2011, 33(6): 43-48.Jiang Jiang, Li Xuan, Chen Yingwu, et al. Evidential network for safety analysis and evaluation of aerospace system[J]. Systems Engineering and Electronics, 2011, 33(6): 43-48. |
| [13] | 姜江, 李璇, 邢立宁, 等. 基于模糊证据推理的系统风险分析与评价[J]. 系统工程理论与实践, 2013, 33(2): 529-537.Jiang Jiang, Li Xuan, Xing Lining, et al. System risk analysis and evaluation approach based on fuzzy evidential reasoning[J]. Systems Engineering——Theory & Practice, 2013, 33(2): 529-537. |
| [14] | Shafer G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976. |
| [15] | 段新生. 证据理论与决策、人工智能[M]. 北京:中国人民大学出版社, 1993.Duan Xinsheng. D-S theory of evidence, decision making and artificial intelligence[M]. Beijing: China Renmin University Press, 1993. |

