2. 中国科学院大学 管理学院, 北京 100190
2. School of Management, University of Chinese Academy of Sciences, Beijing 100190, China
0 引言
经济全球化的背景下, 国家之间繁荣的贸易往来使得全球各大港口吞吐量规模都飞速增长, 世界大港的排序不断刷新. 经过短短三十年, 我国沿海港口实现了跨越式发展. 但是,近年来, 港口之间的竞争范围不断扩大. 而地理位置相近、腹地重合的一些港口之间联系更为密切, 其竞争更加激烈.
港口竞争市场的特殊性在于, 港口之间的竞争不但表现为对市场需求的竞争, 还表现在对于不可再生的自然岸线资源的竞争. 作为整个商品市场供应链的重要节点, 港口之间对腹地货源的运输需求存在着激烈竞争; 同时为了争夺岸线资源, 港口码头无序建设,岸线资源无序开发,已超出了资源环境承载能力. 当前中国经济结构调整步伐加快,对港口协同发展的要求越来越突出, 港口之间的竞争已经不局限于单个港口,而往往是港口群之间的竞争. 本文比较了黄海地区青岛港、日照港、连云港港三个港口采取竞争、合作不同策略对港口收益的影响, 研究结果表明,合作策略有助于提升港口群整体收益.
我国黄海海域沿岸主要包括山东半岛及江苏省大部分地区, 沿线分布着青岛港、日照港、连云港港三个亿吨级大港, 其中日照港岚山港区距连云港北翼赣榆港区仅约70公里, 地理位置非常接近,港口之间面临着激烈的竞争. 这一地区处于环渤海港口群和长三角港口群的中间地带, 同时参与着环渤海及长三角两个港口群的协同发展,在我国大小港口群中, 是一个非常特殊的地带. 本文说明,对这三个港口进行整体规划, 促进合作,有利于黄海地区岸线资源有效利用. 1 文献综述 1.1 港口群研究
港口群的产生是现代国际物流发展的必然要求. 许多研究工作(如肖钟熙[1], 杨静蕾等[2])在界定港口群特性时,提出了横向和纵向两种联合方式, 其中横向是空间意义上的, 即由邻近空间范围内的不同港口个体组成港口群体; 纵向则是产业意义上的,即由某个大型港口为核心, 由相关临港工业、陆运、航运代理、港口服务业等产业组成的纵向产业链. 本文主要探讨横向联合的港口群.
佟成权[3]认为港口群形成需要四大条件: 第一,腹地同一性, 即处于同一经济区域,地理位置相近,自然条件相似; 第二,系统开放性, 港口群内不同港口应信息共享,互相协调合作; 第三,特色互补性, 港口群中各港口应通过优势互补,实现港口群效益最大化; 第四, 功能差异性,港口之间避免趋同,避免资源浪费与恶性竞争. 肖钟熙[1]认为港口群是地理位置相近、经济腹地部分共有、功能可以有一定程度的互相取代且互为竞争对手的若干个港口. 董雷[4]针对港口群的特点, 提出了交通的通达性、空间的临近性、行政管理的有效性三要素, 兼顾港口的经济特性.
综合已有研究成果,本文提出港口群的定义如下: 港口群是地理位置临近、自然条件类似、经济腹地部分共享、优势功能一定程度互补的若干港口的集合, 港口之间互为竞争对手与合作伙伴, 以实现单个港口与港口群整体效益最大化. 1.2 港口竞争合作研究
港口间竞争(inter-port competition)问题是目前港口研究的热点之一. 对这一问题的研究,通常有三种途径: 第一种是界定港口竞争及港口竞争力评价框架,并使用它们进行案例研究, 如Hoyle等[5],陈双喜等[6],刘颖等[7], Notteboom等[8] 等. 第二种是使用计量经济模型进行实证研究, 应用随机前沿分析(stochastic frontier analysis)、时间序列分析或其他计量方法对港口效率进行度量, 如Wu等[9],Lin等[10]. 第三种就是使用博弈模型研究港口竞争,本文即使用这一途径. Verhoeff[11] 是全面研究港口竞争的第一篇文章, 他认为港口市场的市场结构通常是垄断性质的, 为后续对于港口之间博弈竞争的研究,例如Jankowski[12], Hansen[13],Zan[14],Song等[15],Imai等[16], Saeed等[17] 等,奠定了基础.
我国港口博弈领域的研究主要关注于长三角和珠三角地区. 章娴静[18]以上海港和宁波港为例, 探讨了单阶段博弈和重复博弈的不同策略,分析了合作策略所需条件. 董岗[19]结合上海港和宁波港的集装箱港区参数,使用Logit 函数刻画两港区的集装箱需求量,采用逆向归纳法分析纳什均衡结果, 研究了合作博弈情况下的若干问题. 沐潮[20]通过博弈结构转换研究港口合作机制的生成机理, 基于部分合作博弈的竞争本质,给出了深圳港口群部分合作的策略. 王江等[21] 研究了深圳港和香港港的博弈情况, 基于伯特兰模型求解纳什均衡.
港口竞争的特殊性还体现在其空间特性较为明显, 因此Hotelling模型在港口竞争方面得到了广泛应用. 董岗[22]通过扩展的Hotelling模型研究新建港口的位置选择、港口费用的竞争及合作博弈, 研究表明非合作博弈情况下,港口选址趋于集中, 且由于忽略外部性而引起恶性竞争. 周鑫等[23]在改进的Hotelling模型基础上, 构建了多个港口企业合作的定价模型, 比较了竞争与合作情况下多个港口企业市场份额与利润的关系.
我国黄海地区港口主要分布在山东半岛到江苏北部的黄海海岸线上. 这些港口的腹地主要为由华北延伸到西北的我国北方大部分地区, 货种包括煤炭、钢铁等大宗散货,以及以工业产成品为主的集装箱货物. 沿岸青岛港、日照港、连云港港三个港口年吞吐量均在2亿吨以上, 规模相近,加之地理位置紧邻, 构成了黄海海岸线上市场竞争最激烈的区域. 过去研究多关注港口市场对于货运需求的竞争, 对于自然资源的关注则较少. 本文首次从自然资源竞争、市场需求竞争两方面分别探讨黄海地区港口竞争问题. 关于市场需求竞争方面的探讨,本文对经典Hotelling 模型进行扩展, 将传统的两港口博弈模型扩展至三个港口, 以更好体现黄海地区港口群的特征. 同时, 针对黄海地区青岛、日照、连云港三港的地理位置特征, 探讨了空间距离对港口竞争合作的影响. 2 理论分析
港口群内各个港口之间的竞争,一方面是对自然资源, 尤其是海岸线资源的竞争,这主要是通过加快建设靠泊码头来实现的; 另一方面是对市场需求的竞争, 这主要是通过控制港口服务价格、港口装卸效率、通关效率等体现的. 2.1 港口竞争合作研究
对于青岛港、日照港及连云港港进行以下假设.
1)关于竞争机制的假设: 假设三个港口都想扩大自己所拥有的岸线资源. 为达到这一目的,港口确定自己要建造的码头数量. 用 $g_i\in[0,\infty)$ 代表第$i$个港口建造的码头数,$i=1,2,3$; $G=\sum_{i=1}^3 g_i$,代表黄海岸线上所建设码头的总数量; $v$代表每个码头的收益.
2)关于收益函数的假设: 假设每个码头的收益$v$是黄海岸线上各个港口所建设码头数量加权平均$G_i=\lambda_{i1}g_1+\lambda_{i2}g_2+\lambda_{i3}g_3$ 的函数: \begin{eqnarray} v=v(G_i),\label{eq:1}\nonumber \end{eqnarray} 其中$\lambda_{ij}>0$表示港口$j$的码头数量对于港口$i$码头收益的影响系数, $\sum_{j=1}^3\lambda_{ij}=1$,$i,j=1,2,3$.
腹地资源是有限的. 因此,整个黄海岸线上所建码头越多, 每个码头盈利越少. 同时假设由于岸线资源有限, 码头盈利减少的程度也随码头数量增加而加剧, 因此得到收益函数$v$的一阶和二阶条件如下: \begin{eqnarray} \frac{\partial v}{\partial G}<0,\; \frac{\partial^2 v}{\partial G^2}\leq 0. \label{eq:2}\nonumber \end{eqnarray}
收益函数边界条件设定: 考虑实际情况,假定收益函数非负, 即整个黄海地区存在一个最大可建设码头数量$G_{\max}$使得: \begin{eqnarray} \left\{\begin{array}{cc} v(G)>0,& G<G_{\max}\\ v(G)=0,& G\geq G_{\max}(1) \end{array}\right. \label{eq:3} \end{eqnarray} 例如,当$\alpha,\beta>0$时,如下形式的$v(G)$即满足要求: \begin{eqnarray} v(G) = \left\{\begin{array}{ll} \alpha-\beta G,& G<\frac{\alpha}{\beta},\\[3mm] 0,& G\geq \frac{\alpha}{\beta}. \end{array}\right.\label{eq:vGlinear} \nonumber \end{eqnarray}
3)求解纳什均衡: 每个港口选择$g_i$,以最大化自己的利润. 假定建设一个码头的成本为$c$,则每个港口的利润函数为: \begin{eqnarray} \pi_i(g_1,g_2,g_3)=g_iv\left(G_i\right)-g_ic,\; i=1,2,3 \label{eq:4}(2) \end{eqnarray}
最优化一阶条件为: \begin{eqnarray} \frac{\partial \pi_i}{\partial g_i}=v(G_i)+g_i\lambda_{ii} v'(G_i)-c =0,\; i=1,2,3 .\label{eq:5} \nonumber \end{eqnarray}
观察一阶条件,增加一个码头有两方面的效应: 一方面, 建设码头本身带来一定的收益$v$; 另一方面, 新增码头使得该港口的原有码头收益下降($g_iv'<0$).
上述3个一阶条件定义了3个最优反应函数,联立求解得到纳什均衡: \begin{eqnarray} g^* = (g_1^*,g_2^*,g_3^*) \label{eq:6}(3) \end{eqnarray}
因此,纳什均衡下整个黄海地区总建设码头数为 \begin{eqnarray} G^* = \sum_{i=1}^3 g_i^* \label{eq:7}(4) \end{eqnarray}
命题1 在靠近边界收益的条件下,若某个港口决定增建码头, 对其他港口规划建设码头数目有负向影响.
证明 不失一般性,现固定$g_3$, 将$g_1$和$g_2$视为$g_3$的函数,考虑如下的一阶条件 \arraycolsep 2pt \begin{eqnarray} v(G_1)+g_1\lambda_{11} v'(G_1)-c &=& 0,\nonumber\\ v(G_2)+g_2\lambda_{22} v'(G_2)-c &=& 0 .\nonumber \end{eqnarray} 注意到以上的两个一阶条件可以唯一确定$g_1$和$g_2$, 于是对其分别求关于$g_3$的导数,得到 \begin{eqnarray} \left(\lambda_{11}g_1v''(G_1)+v'(G_1)\right)\left(\lambda_{11}\frac{\partial g_1}{\partial g_3}+\lambda_{12}\frac{\partial g_2}{\partial g_3}+\lambda_{13} \right)+\lambda_{11} v'(G_1)\frac{\partial g_1}{\partial g_3} &=& 0,\nonumber\\ \left(\lambda_{22}g_2v''(G_2)+v'(G_2)\right)\left(\lambda_{21}\frac{\partial g_1}{\partial g_3}+\lambda_{22}\frac{\partial g_2}{\partial g_3}+ \lambda_{23}\right)+\lambda_{22} v'(G_2)\frac{\partial g_2}{\partial g_3} &=& 0 .\nonumber \end{eqnarray} 将其整理之后得到 \begin{eqnarray} (2\lambda_{11}v'(G_1)+\lambda_{11}^2g_1v''(G_1))\frac{\partial g_1}{\partial g_3}+ \lambda_{12}\left(\lambda_{11}g_1v''(G_1)+v'(G_1)\right)\frac{\partial g_2} {\partial g_3} &=\\& -\lambda_{13}\left(\lambda_{11}g_1v''(G_1)+v'(G_1)\right) ,\nonumber\label{eq:g1g3}\\ \lambda_{21}\left(\lambda_{22}g_2v''(G_2)+v'(G_2)\right)\frac{\partial g_1}{\partial g_3}+(2\lambda_{22}v'(G_2)+\lambda_{22}^2g_2v''(G_2)) \frac{\partial g_2}{\partial g_3} &=\\& -\lambda_{23}\left(\lambda_{22}g_2v''(G_2)+v'(G_2)\right). \nonumber \end{eqnarray}
定义 \begin{eqnarray} r_1 &=& 1+\lambda_{11}g_1\frac{v''(G_1)}{v'(G_1)},\nonumber\\ r_2 &=& 1+\lambda_{22}g_2\frac{v''(G_2)}{v'(G_2)}. \nonumber \end{eqnarray} 以上的方程组可以转化为 \begin{eqnarray} \bigg(\lambda_{11}+\frac{\lambda_{11}}{r_1}\bigg)\frac{\partial g_1}{\partial g_3} + \lambda_{12}\frac{\partial g_2}{\partial g_3} &=& -\lambda_{13},\nonumber\\ \lambda_{21}\frac{\partial g_1}{\partial g_3} + \bigg(\lambda_{22}+\frac{\lambda_{22}}{r_2}\bigg)\frac{\partial g_2}{\partial g_3} &=& -\lambda_{23}.\nonumber \end{eqnarray}
解如上方程可得 \begin{eqnarray} \frac{\partial g_1}{\partial g_3} &=& - \frac{1}{\Delta_3}\left(\lambda_{22}\lambda_{13}\bigg(1+\frac{1}{r_2}\bigg)-\lambda_{12}\lambda_{23}\right)\label{eq:pg1pg3}\\(5) \frac{\partial g_2}{\partial g_3} &=& - \frac{1}{\Delta_3}\left(\lambda_{11}\lambda_{23}\bigg(1+\frac{1}{r_1}\bigg)-\lambda_{21}\lambda_{13}\right)\label{eq:pg2pg3}(6) \end{eqnarray} 其中 \begin{eqnarray} \Delta_3 = \lambda_{11}\lambda_{22}\bigg(1+\frac{1}{r_1}\bigg)\bigg(1+\frac{1}{r_2}\bigg)-\lambda_{12}\lambda_{21}. \nonumber \end{eqnarray}
定义如下矩阵 \begin{eqnarray} \Lambda = \left(\begin{array}{ccc} \lambda_{11} & \lambda_{12} & \lambda_{13} \\ \lambda_{21} & \lambda_{22} & \lambda_{23} \\ \lambda_{31} & \lambda_{32} & \lambda_{33} \end{array}\right).\nonumber \end{eqnarray}
注意到在靠近收益边界的时候,由于$v'(G)\rightarrow 0$, 于是可以假设$r_1=r_2=\infty$. 根据表达式(5)和(6),当选取 \begin{eqnarray} \Lambda = \left(\begin{array}{ccc} \lambda & \mu & \mu \\ \mu & \lambda & \mu \\ \mu & \mu & \lambda \end{array}\right)\label{eq:Lambda}(7) \end{eqnarray} 且$\lambda\neq \mu$时,可以得到 \begin{eqnarray} \frac{\partial g_1}{\partial g_3} &=& - \frac{\mu}{\lambda+\mu} <0 ,\nonumber\\ \frac{\partial g_2}{\partial g_3} &=& - \frac{\mu}{\lambda+\mu} <0. \nonumber \end{eqnarray} 这表明港口1和2的码头数量随着港口3的码头数量的增加而减少.
同样的,在$v''(G)=0$的条件下,也可以类似地导出如上的递减关系.
命题1说明,在港口资源趋于饱和的条件下, 港口的最优码头数量除了取决于自身码头数量以外, 还随着其他港口码头数的增加而递减. 这表明, 黄海地区各港口之间对岸线资源存在着竞争关系. 实际上,多增加的码头, 使得所有港口新建码头的决策所能带来的边际收益均有所减少.
命题2 纳什均衡下的总码头建设数量大于环渤海港口群整体最优码头建设数量.
观察最优化一阶条件可知,在每个港口的最优决策点上, 个体边际成本小于社会总体边际成本. 每个港口在决定建设新码头时, 仅考虑了新码头对本港口现有码头的负向影响, 并未考虑到它给整个黄海地区现存码头的负向影响, 即并未考虑外部性成本. 不考虑外部性成本的情况下, 每个港口单独决策建设码头数量后, 纳什均衡下的总的码头建设数量大于黄海港口群整体最优码头建设数量.
证明 在纳什均衡及耦合权矩阵满足(7)的条件下, 设最优码头数量为$G^*$. 考虑到耦合矩阵的对称性, 则$g_1^*=g_2^*=g_3^*=\frac{G^*}{3}$,将3 个一阶条件加总得 \begin{eqnarray} v\left(\frac{G^*}{3}\right) + \lambda\frac{G^*}{3}v'\left(\frac{G^*}{3}\right)=c \label{eq:11}(8) \end{eqnarray}
而整个黄海地区港口群的最优目标则是最大化群内港口总利润, 此时的耦合系数应是均衡的,即$\lambda=\mu=\frac{1}{3}$,于是可得 \begin{eqnarray} \max_{G} G\left(v\left(\frac{G}{3}\right) -c\right)(9) \end{eqnarray}
最优化一阶条件为: \begin{eqnarray} v\left(\frac{G^{**}}{3}\right) + \frac{G^{**}}{3}v'\left(\frac{G^{**}}{3}\right)=c(10) \end{eqnarray}
考虑到$\lambda<1$,比较式(8)与式(10)可知,$G^*>G^{**}$, 即证明海岸线资源被过度使用,这是港口无规划竞争造成的后果. 2.2 市场需求竞争
针对市场需求的竞争是港口竞争的另一方面.
港口所提供的产品主要是货物吞吐. 如果不考虑航线安排的差异, 港口所能提供的产品(这里是港口装卸及其配套服务)差异性不大, 对市场需求的竞争主要存在于空间位置的竞争和航线安排的竞争上. 航线安排需要整个航运产业链的协调配合,属于纵向竞争, 这里不进行探讨. 本部分主要探讨由港口空间差异导致的竞争与合作.
港口与普通生产厂商不同. 生产厂商可以通过确定生产计划从而控制产量, 而港口多是被动服务于进出港货物, 一般不会通过制定生产计划控制产量(即吞吐量),与普通厂商相比, 港口企业的产量控制能力很弱. 因此,假定竞争是主要通过定价来实现的.
Hotelling模型是处理两竞争者存在空间差异的经典博弈模型. 本文将经典Hotelling模型进行扩展,将一维空间差异扩展至二维, 以求更符合实际.
1)对于港口的假设: 仍以青岛港、日照港和连云港港为例. 假设青岛港位于$(0,0)$,日照港位于$(a,0)$,连云港港位于$(1,0)$上, 且位置不重叠,即$0<a<1$.
2)对于需求的假设: 假设货物从货源地到港口的成本与其陆上运输距离成比例, 单位距离陆上运输成本为$w$. 假定货源地为$(0,0)$、$(0,1)$、$(1,1)$、$(1,0)$所组成的矩形, 发货人均匀分布于矩形之中.
3)对于竞争机制的假设: 假定这三个港口通过定价和提供差异化服务进行竞争. 三个港口同时对其服务费用进行定价,令$p_i$为港口$i$的价格, $i=1,2,3$. $D_i(p_1,p_2,p_3)$为需求函数. 每个港口提供服务, 这里主要是装卸服务. 在地理位置相同的情况下,港口自然条件差异不大, 可近似认为港口提供服务所需成本无差异,令其为$c$.
存在这样两个横坐标$t_1,t_2$,使得当发货人位置横坐标$x<t_1$时, 货物将在青岛港$(0,0)$装卸; 当$x\geq t_2$时, 货物将在连云港港$(1,0)$装卸. 因此,两港的市场份额分别为: \begin{eqnarray} D_1&=& \int_{0}^{1}\int_{0}^{t_1}{\rm d}x{\rm d}y = t_1 \label{eq:14}(11)\\ D_2&=& \int_{0}^{1}\int_{t_1}^{t_2}{\rm d}x{\rm d}y = t_2-t_1 \label{eq:15}(12)\\ D_3&=& \int_{0}^{1}\int_{1}^{t_2}{\rm d}x{\rm d}y = 1-t_2 \label{eq:16}(13) \end{eqnarray}
这里,$t_1,t_2$满足: \begin{eqnarray} \begin{cases} t_1 = \frac{1}{2w}(aw+p_2-p_1) \\ t_2 = \frac{1}{2w}((1+a)w+p_3-p_2)(14) \end{cases}\label{eq:17} \end{eqnarray}
三个港口的需求份额分别为: \begin{eqnarray} \begin{cases} D_1= \int_{0}^{1}\int_{0}^{t_1}{\rm d}x{\rm d}y = t_1 = \frac{1}{2w}(aw+p_2-p_1)\\ D_2= \int_{0}^{1}\int_{t_1}^{t_2}{\rm d}x{\rm d}y = t_2-t_1 =\frac{1}{2w}(w+p_3-2p_2+p_1)\\ D_3= \int_{0}^{1}\int_{t_2}^{1}{\rm d}x{\rm d}y = 1-t_2= 1-\frac{1}{2w}((1+a)w+p_3-p_2)(15) \end{cases}\label{eq:18} \end{eqnarray}
三个港口的利润函数分别为: \begin{eqnarray} \begin{cases} R_1= (p_1-c)D_1 = (p_1-c)\left(\frac{1}{2w}(aw+p_2-p_1)\right)\\ R_2= (p_2-c)D_2 = (p_2-c)\left(\frac{1}{2w}(w+p_3-2p_2+p_1)\right)\\ R_3= (p_3-c)D_3 = (p_3-c)\left(1-\frac{1}{2w}((1+a)w+p_3-p_2)\right)(16) \end{cases}\label{eq:19} \end{eqnarray}
为达到利润最大化,三个港口分别确定自己的定价. 即在二阶条件满足的情况下,对利润函数分别求一阶最大化条件, 得港口的最优反应函数分别如下:\vspace{2mm} \begin{eqnarray} \begin{cases} \frac{\partial R_1}{\partial p_1} = \frac{1}{2w}(aw+p_2-2p_1+c)=0\\ \frac{\partial R_2}{\partial p_2} = \frac{1}{2w}(w+p_3-4p_2+p_1+2c)=0\\ \frac{\partial R_3}{\partial p_3} = 1-\frac{1}{2w}((1+a)w+2p_3-p_2-c)=0 \end{cases} \label{eq:20}(17) \end{eqnarray}
将三个最优反应函数联立求解,得博弈均衡解为: \begin{eqnarray} \begin{cases} p_1^* = c+\frac{(1+2a)w}{4}\\ p_2^* = c+\frac{w}{2}\\ p_3^* = c+\frac{(3-2a)w}{4} \end{cases}\label{eq:21}(18) \end{eqnarray}
三个港口的市场份额分别为: \begin{eqnarray} \begin{cases} D_1 = \frac{1+2a}{8}\\ D_2 = \frac{1}{2}\\ D_3 = \frac{1}{2} -\frac{1+2a}{8} \end{cases} \label{eq:22}(19) \end{eqnarray} \vspace{1mm}
在港口服务成本相同的条件下,三港的需求份额取决于港口位置.
港口的利润分别为: \begin{eqnarray} \begin{cases} R_1 = \frac{1}{4}w\frac{(1+2a)^2}{8}\\ R_2 = \frac{1}{4}w\\ R_3 = \frac{1}{4}w\frac{(3-2a)^2}{8} \end{cases}\label{eq:23}(20) \end{eqnarray} \vspace{1mm}
容易看出,在单位距离成本不变的情况下,港口的利润主要取决于:
1)货物从货源地运输至港口的单位成本. 如果从货源地至港口的单位运输成本越高, 相当于港口所提供的产品(货物吞吐)的差异性就越大, 每个港口对附近货源的垄断能力就越强,港口之间的竞争强度降低, 港口盈利能力越大.
2)港口位置. 港口服务成本区别不大的条件下, 港口位置决定货物运输的成本,也因此决定着港口对腹地资源的占有份额.
对黄海地区港口而言,其货源腹地包括华北至西北的大部分地区, 辽阔的腹地条件使得港口群内港口之间的空间差异非常小, 而相同的自然资源条件使得港口之间的服务成本差异也非常小, 所提供的产品(货物吞吐)差异性也因此非常小. 港口的自然垄断特性表现得不明显,更多地表现出竞争性市场的特征. 2.3 合作策略
假设山东省的青岛港与日照港展开合作关系.
1)对于港口的假设: 仍然假设青岛港位于$(0,0)$,日照港位于$(a,0)$, 连云港港位于$(1,0)$上,且位置不重叠,即$0<a<1$.
2)对于需求的假设: 仍然假设货物从货源地到港口的成本与其陆上运输距离成比例, 单位距离陆上运输成本为$w$. 货源地为$(0,0)$、$(0,1)$、$(1,1)$、$(1,0)$所组成的矩形, 发货人均匀分布于矩形之中.
3)对于竞争机制的假设: 令$p_i$为港口$i$的价格,$i=1,2,3$. 假定青岛港与日照港合作定价,从而与连云港港进行竞争,即$p_1=p_2$. 仍然认为港口提供服务所需成本无差异.
这样,青岛港、日照港的需求份额加总为: \begin{eqnarray} D_{12}(p_2,p_3) = \int_{0}^{1}\int_{0}^{t_2}{\rm d}x{\rm d}y = \frac{1}{2w}((a+1)w+p_3-p_2) \label{eq:24}(21) \end{eqnarray}
连云港港的需求与上小节一致: \begin{eqnarray} D_{3}(p_2,p_3) = 1- D_{12} = 1-\frac{1}{2w}((a+1)w+p_3-p_2) \label{eq:25}(22) \end{eqnarray}
港口利润函数分别为: \begin{eqnarray} \begin{cases} R_{12}(p_2,p_3) = (p_2-c)D_{12}(p_2,p_3) = (p_2-c)\frac{1}{2w}((a+1)w+p_3-p_2)\\ R_{3}(p_2,p_3) = (p_3-c)D_{3}(p_2,p_3) = (p_3-c)\left(1-\frac{1}{2w}((a+1)w+p_3-p_2)\right) \end{cases}\label{eq:26}(23) \end{eqnarray}
在二阶条件满足的情况下,对两个利润函数分别求一阶最大化条件, 得港口最优反应函数分别如下: \begin{eqnarray} \begin{cases} \frac{\partial R_{12}}{\partial p_2} = \frac{1}{2w}((a+1)w+p_3-2p_2+c)=0\\ \frac{\partial R_3}{\partial p_3} = 1-\frac{1}{2w}((a+1)w+2p_3-p_2-c)=0 \end{cases}\label{eq:27}(24) \end{eqnarray}\vspace{1mm}
将最优反应函数联立求解,得博弈均衡解为:\vspace{1mm} \begin{eqnarray} \begin{cases} p_2^* = c+\left(1+\frac{a}{3}\right)w\\ p_3^* = c+\left(1-\frac{a}{3}\right)w \end{cases}\label{eq:28}(25) \end{eqnarray}
三个港口的市场份额分别为: \begin{eqnarray} \begin{cases} D_{12} = \frac{1}{2}+\frac{a}{6}\\ D_2 = \frac{1}{2}-\frac{a}{6} \end{cases} \label{eq:29}(26) \end{eqnarray}
三个港口的利润分别为: \begin{eqnarray} \begin{cases} R_{12} = \frac{(3+a)^2}{18}w\\ R_3 = \frac{(3-a)^2}{18}w \end{cases}\label{eq:30}(27) \end{eqnarray}
命题3 港口合作将获得高于竞争的利润.
证明 将港口1、2合作后的利润比竞争条件下各自利润加总后易知 \begin{eqnarray} \frac{R_{12}}{R_1+R_2} = \frac{\frac{1}{18}(3+a)^2}{\frac{1}{4}(1+\frac{(1+2a)^2}{8})} >1 \label{eq:31} \end{eqnarray}
命题4 合作策略可提高整个港口群的利润水平.
证明 由于命题3已证,下面仅需证明在合作情况下, 未参加合作的港口连云港港的利润水平也比非合作情况下有提高. 在$0<a<1$ 的假设下, $\frac{(3-a)^2}{18}w>\frac{1}{4}w\frac{(3-2a)^2}{8}$ 是显然的, 后面我们会用数值模拟说明这一点.
命题5 港口合作收益,与合作港口之间的距离正相关. 容易看出,进行合作的青岛港、日照港的总利润同样取决于两部分, 即单位陆上运输成本$w$和日照港的地理位置$a$. 如前所述, 陆上单位运输成本是港口服务产品差异的来源,影响着港口的垄断特性. 在单位陆上运输成本$w$不变的情况下, 合作港口即青岛港和日照港之间的距离$a$越大,$R_{12}$ 越大, 那么港口合作的效益更大. 2.4 结果分析与数值模拟
为便于比较,将竞争以及合作的博弈均衡结果及相应的计算结果列表, 如表 1所示.
可以看出, 合作策略使得青岛港和日照港联合确定的价格明显高于港口群内非合作的连云港港. 另外, 基于空间差异的港口合作保证了提价行为并不会造成两港市场份额的减少. 因此,青岛港和日照港的合作显然可以给两个港口整体带来更多的收益. 为了更直观地说明这一点,进行一个数值模拟.
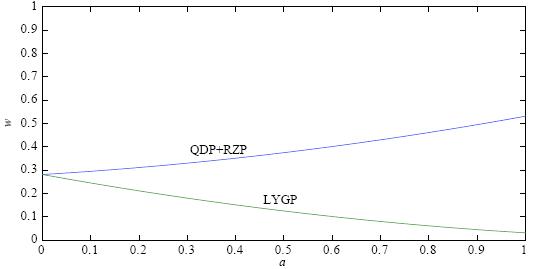
假设参数$a$(即中间港口的位置, 这里即日照港的位置)在单位面积内由$0$变到$1$. 以单位$w$计的港口利润计算结果如图. 为便于比较, 将竞争策略下的青岛港和日照港利润也进行加总. 采用竞争策略的青岛港、日照港及连云港港利润水平如图 1; 采用合作策略的青岛港、日照港及连云港港利润水平如图 2.
采用竞争策略的情况下(如图 1), 青岛港和日照港利润总和的最大值与采用合作策略的青岛港及日照港利润总和(如图 2)最小值相近. 由数值模拟直观地证明了命题3, 即合作策略比竞争策略可获得更大的利润. 另外可证, 合作的存在事实上提高了黄海地区港口群的整体利润水平, 港口群内部分港口合作不仅使得合作港口受益, 也可提高整个港口群的利润水平,命题5 得证.
 |
| 图 1 采用竞争策略的三港利润水平 |
如图 2,随着参数$a$的增加,即随着青岛港和日照港之间距离的扩大, 青岛港和日照港合作的利润水平上升,连云港港利润水平下降. 即命题4 得证.
 |
| 图 2 采用合作策略的三港利润水平 |
据调研, 青岛港目前有大港区、黄岛港区、前湾新港区和董家口港区四大港区, 目前有码头15 座,泊位82个. 日照港自有海岸线约100公里, 规划有石臼、岚山两大港区,占据岸线长度共32公里,拥有码头9 座, 未来规划吞吐能力6亿吨. 连云港港目前拥有主体连云港区、北翼赣榆和前三岛港区, 南翼徐圩和灌河港区,规划港口岸线100.7 公里,码头数目6个.
目前,黄海地区港口整合主要经历了如下几个阶段: 日照港于2003年与岚山港联合重组为日照港集团,改善了治理体制; 青岛港于2007 年与日照港合资成立日青集装箱公司, 与日照港两个集装箱泊位进行合作. 尽管该地区港口群已经进行了初步的港口资源整合,整合效果却差别很大, 急需进行更大范围、更深层次的战略合作. 3 结论与建议
本文通过建立黄海地区港口自然资源博弈模型以及市场竞争博弈模型, 说明过度竞争的出现,不但导致港口各自利益受损, 更重要的危害是过度使用不可再生的岸线资源. 资源的过度使用, 将恶化滨海生态环境,影响地区经济可持续发展. 而地理位置适当的两港口若能进行有效合作, 则不仅合作港口会获得高于非合作博弈的利益, 同时港口群整体的收益水平将有所提升. 针对以上结论, 提出政策建议如下:
1)建议成立"黄海港口群",尊重港口依据自然地理位置整合的需求, 打破行政区划.
据调研,连云港港不仅地理位置上与山东日照港极为接近, 货种货源也呈现较大同质性,更多表现出北方枢纽港口的特征. 但由于连云港港、日照港、青岛港分属江苏省、山东省不同行政区划, 给统一管理带来一定的困难. 建议黄海地区港口加强整合, 青岛港、日照港、连云港港进行统一规划,保护岸线资源.
2)政府要在更高的层面上对于港口的建设发展做出统一安排, 加强港口企业的协同合作. 港口企业需对目标形成共识, 发挥各自竞争优势,各自贡献能力形成合力.
黄海地区虽然有丰富的岸线资源,但港口群内呈现激烈的竞争. 另外, 这一地区服务于北方大部分省份,货源腹地高度重合. 港口企业需发挥各自的竞争优势,集中力量发展优势货种码头. 目前, 有必要对该地区港口功能定位进行重新规划, 使得各港口各自贡献能力而形成合力.
3)建立港口之间多边协调制度,加强港口联盟的制度约束机制.
港口行业属于自然垄断行业,容易形成寡头. 不合理竞争固然会损害港口利益,但寡头的形成也会干扰市场秩序. 必要时需要对港口合作做出一定限制, 防止操纵价格、干扰市场的行为出现. 合作港口要遵守行业规范, 加强自律,增进信任机制,协调利益分配. 4 致谢
感谢国家自然科学基金委员会(71373262,71390330, 71390331)对本文研究工作的支持.
本文是在汪寿阳教授指导下完成的. 2011年和2013年, 他两次带队赴我国东部沿海进行港口群调研, 引导科研团队研究世界名港的兴衰及其对中国港口发展的启示. 感谢中国科学院预测科学研究中心世界港口研究小组的老师和同学们对本文研究的建议.
| [1] | 肖钟熙. 港口群的概念与港口布局规划[J]. 水运管理, 2007, 29(6): 11-13.Xiao Zhongxi. The concepts of ports cluster and ports allocation layout[J]. Shipping Management, 2007, 29(6): 11-13. |
| [2] | 杨静蕾, 李欣. 港口群内港口间协调发展评价[J]. 上海海事大学学报, 2009, 30(3): 54-58. Yang Jinglei, Li Xin. Evaluation of coordination development among seaports in same port cluster[J]. Journal of Shanghai Maritime University, 2009, 30(3): 54-58. |
| [3] | 佟成权. 港口群的群体效应理论及其运量分配模型的研究[J]. 大连海事大学学报, 1993, 19(3): 319-326.Tong Chengquan. The study on the theory of population effect of ports cluster and its shipping distribution model[J]. Journal of Dalian Maritime University, 1993, 19(3): 319-326. |
| [4] | 董雷, 刘凯. 港口群的发展趋势与发展战略研究[J]. 综合运输, 2010(1): 33-35. Dong Lei, Liu Kai. Research on trends and development strategy of port group[J]. Comprehensive Transportation, 2010(1): 33-35. |
| [5] | Hoyle B, Charlier J. Inter-port competition in developing countries: An East African case study[J]. Journal of Transport Geography, 1995, 3(2): 87-103. |
| [6] | 陈双喜, 戴明华. 港口竞争力评价模型与东北亚港口竞争力的评价[J]. 大连海事大学学报(社会科学版), 2006, 5(4): 39-43. Chen Shuangxi, Dai Minghua. Ports competition evaluation model and application in Northeast Asia Ports[J]. Journal of Dalian Maritime University (Social Science Edition), 2006, 5(4): 39-43. |
| [7] | 刘颖, 姜泰元. 基于层次分析法的港口供应链管理的研究[J]. 生产力研究, 2012(2): 111-112. Liu Ying, Jiang Taiyuan. Research of port supply chain management based on AHP[J]. Productivity Research, 2012(2): 111-112. |
| [8] | Notteboom T, Yap W Y. Port competition and competitiveness[J]. The Blackwell Companion to Maritime Economics, 2012: 549-570. |
| [9] | Wu Y C J, Goh M. Container port efficiency in emerging and more advanced markets[J]. Transportation Research Part E: Logistics and Transportation Review, 2010, 46(6): 1030-1042. |
| [10] | Lin L C, Tseng L A. Application of DEA and SFA on the measurement of operating efficiencies for 27 international container ports[C]// Proceedings of the Eastern Asia Society for Transportation Studies, 2005: 592-607. |
| [11] | Verhoeff J. Seaport competition: Some fundamental and political aspects[J]. Maritime Policy & Management, 1981, 8(1): 49-60. |
| [12] | Jankowski W. The development of liner shipping conferences: A game theoretical explanation[J]. International Journal of Transport Economics, 1989, 16(3): 313-328. |
| [13] | Hansen M. Airline competition in a hub-dominated environment: An application of noncooperative game theory[J]. Transportation Research Part B: Methodological, 1990, 24(1): 27-43. |
| [14] | Zan Y. Analysis of container port policy by the reaction of an equilibrium shipping market[J]. Maritime Policy & Management, 1999, 26(4): 369-381. |
| [15] | Song D-W, Panayides P M. A conceptual application of cooperative game theory to liner shipping strategic alliances[J]. Maritime Policy & Management, 2002, 29(3): 285-301. |
| [16] | Imai A, Nishimura E, Papadimitriou S, et al. The economic viability of container mega-ships[J]. Transportation Research Part E: Logistics and Transportation Review, 2006, 42(1): 21-41. |
| [17] | Saeed N, Larsen O I. An application of cooperative game among container terminals of one port[J]. European Journal of Operational Research, 2010, 203(2): 393-403. |
| [18] | 章娴静. 港口竞争合作博弈分析——以上海港和宁波港为例[J]. 物流工程与管理, 2009(9): 13-15. Zhang Xianjing. Analysis of game theory for competition of ports[J]. Logistics Engineering and Management, 2009(9): 13-15. |
| [19] | 董岗. 基于Logit模型的集装箱港区合作博弈[J]. 现代管理科学, 2011(3): 40-42.Dong Gang. Container port cooperative game analysis based on Logit model[J]. Modern Management Science, 2011(3): 40-42. |
| [20] | 沐潮. 基于部分合作博弈的深圳集装箱港口策略选择[J]. 综合运输, 2009(3): 70-74. Mu Chao. Shenzhen's container ports strategy selection based on partially cooperative game theory[J]. Comprehensive Transportation, 2009(3): 70-74. |
| [21] | 王江, 罗宇源. 基于伯特兰德模型的深圳港与香港港港口定价博弈[J]. 水运管理, 2009, 31(3): 17-20.Wang Jiang, Luo Yuyuan. The pricing strategy of ports in Shenzhen and Hong Kong based on Bertrand's model[J]. Shipping Management, 2009, 31(3): 17-20. |
| [22] | 董岗. 基于豪泰林模型的港口竞合博弈分析[J]. 交通科技与经济, 2010, 12(2): 122-124. Dong Gang. Analyzing ports co-competition game based on Hotelling model[J]. Technology and Economy in Areas of Communications, 2010, 12(2): 122-124. |
| [23] | 周鑫, 沙梅, 郑士源, 等. 基于空间区位模型的港口企业合作定价策略[J]. 上海交通大学学报, 2011, 45(1): 125-129. Zhou Xin, Sha Mei, Zheng Shiyuan, et al. Pricing strategy of port enterprises under cooperation condition based on located spatial model[J]. Journal of Shanghai Jiaotong University, 2011, 45(1): 125-129. |



