0 引言
突发事件是指突然发生, 造成或者可能造成重大人员伤亡、财产损失、生态破坏和社会危害的公共事件; 应急救援是指突发事件发生后, 迅速展开的挽救人员生命、减少财产损失、恢复生态环境和稳定社会局面的各种紧急救助及处置活动[1]. 突发事件应急救援的调度问题, 研究如何合理地安排救援活动及配置应急资源, 并对应急救援的全过程进行协调与优化, 确保救援活动的有序实施及预期目标的高效实现[2]. 我国自经历了2003年"非典''事件以来, 对突发事件的应急管理给予了高度的重视. 2006年1月国务院发布了"国家突发公共事件总体应急预案'', 根据突发公共事件的发生过程、性质和机理, 将突发事件主要分为自然灾害、事故灾难、公共卫生事件和社会安全事件四大类[3].
近年来,随着我国经济的高速发展,企业生产规模也呈急速增长趋势, 然而与之相关的生产管理水平及安全设施却相对滞后, 导致重特大生产事故频繁发生,对人民生命、财产及环境造成了重大威胁. 对于重特大突发事件的处理,事前的应急预案制定极为重要; 而当事故发生后, 对事故的有效处理则是遏制其恶化或不良后果扩散的关键. 然而, 目前我国多数企业对重大突发生产事故处理还存在很多问题. 根据佘廉等[4]进行的一项调查发现,当突发事故发生后, 缺乏有效的应对方案占到了导致事故扩散原因的38.2%. 而现有的预案又存在诸多问题, 如可操作性不强、系统性不够、无法及时更新等等. 由此可见, 制定一个有效的应急预案并在执行过程中对其进行合理的调整对于减轻事故影响具有非常重要的作用.
本文基于上述现实情况,将前摄性调度与反应性调度两种方法相结合, 通过二者的集成优化,得到企业生产事故与突发事件的最优应急救援计划, 并在执行过程中实现对其的最优调整. 前摄性调度(proactive scheduling)是指在突发事件发生前,基于对未来不确定因素的预测和分析, 通过适当地设置时间冗余形成鲁棒性基准计划, 从而对应急救援的准备及实施提供指导[5, 6]. 反应性调度(reactive scheduling)是指在突发事件发生后, 基于对应急救援过程中实际变化情况的掌握, 借助合适的在线调度策略对基准救援计划进行动态调整, 以确保应急救援目标的有效实现[7, 8]. 就应对突发事件应急救援的不确定性来说, 前摄性调度和反应性调度之间存在着如下的权衡关系[9]: 如果在前摄性调度中增加时间冗余提高基准计划的鲁棒性, 那么在随后的反应性调度中对计划的调整次数便可减小, 从而使得救援过程能够更为平稳顺利地实施; 但是, 此时由于内嵌了较多的时间冗余,应急救援基准计划的效率通常会比较低. 相反,如果在前摄性调度中减少时间冗余, 那么基准计划的效率便可得到有效提高; 但是, 此时由于基准计划鲁棒性的下降,其在反应性调度中的调整次数便会增加, 而过多的变更和调整无疑会给救援的组织带来混乱, 并最终对救援目标的实现造成不良影响.
根据上述讨论, 本文以企业生产事故与突发事件为主要背景,将突发事件应急救援前摄性调度与反应性调度的集成优化问题定义如下: 在救援活动工期的随机变化条件下, 研究如何通过前摄性调度生成鲁棒性基准计划, 并在计划执行中通过反应性调度合理地对其进行动态调整, 以使救援过程能够顺利进行,从而最为有效地实现预定的救援目标. 在论文的后续部分,作者首先对所研究问题进行界定, 构建相应的优化模型; 随后,设计问题求解的禁忌搜索启发式算法, 通过一个实际案例对研究进行说明; 最后给出研究结论. 1 问题界定
企业生产事故等突发事件的应急救援从启动到结束, 具有明显的"一次性''特征. 因此, 在对其应急救援一般过程进行分析的基础上,可以借鉴项目网络的表述方式, 基于各救援活动之间的内在逻辑关系,将它们表示成一个AoN (Activity-on-Node)网络[10]. 现假定某一突发事件应急救援活动网络为$G=(N,A$),其中, $N$为网络节点的集合,表示活动; $A$ 为网络箭线的集合, 表示活动之间的逻辑关系. 集合$N$由$n$个活动构成, 活动1和$n$分别是因网络表示需要而添加的虚的开始和结束活动. 非虚救援活动$i$ ($i=2,3,\cdots,n-1$) 的完成需要投入$K$种资源, 其中,对第$k$ ($k=1,2,\cdots,K$)种资源需求量为$r_i^k$(虚活动1和$n$对任何一种资源的需求量均定义为0). 在 进行应急救援时,每种资源的总可用量是有限的, 第$k$种资源的可用量为$R^k$.
通常,为了在突发事件发生后能够快速高效地展开应急救援工作, 事先需要编制针对性的应急预案及应急基准计划,以便为突发事件应急救援的准备与实施提供指导. 应急基准计划的编制属于前摄性调度的范畴. 显然, 为了应对突发事件应急救援本身所固有的高度不确定性, 基准计划必须具有一定的鲁棒性,否则, 它将会由于频繁的调整失去其对应急救援的实际指导作用. 对于上述定义的活动网络$G=(N,A$),在给定的资源投入水平下, 考虑到应急 救援内外部环境的不确定性, 将活动$i$的工期定义为一个均值为${\mu}_i$、标准差为${\sigma}_i$的随机变量$\tilde{d_i}$.现实中, ${\mu}_i$ 和${\sigma}_i$可以基于同类救援活动的历史统计数据, 结合专家的分析判断进行估计. 现将活动$i$的基准开始时间表示为$s_i^b$,假定在编制应急基准计划时, 整个救援过程的期限设定为$D$,则前摄性调度问题可界定为: 在救援期限$D$的约束下合理地安排$s_i^b$, 以使时间缓冲在活动之间得到有效的分配,从而取得基准计划 鲁棒性的最大化.
由于突发事件应急救援的不确定性(在本文中用救援活动工期的随机性体现), 在应急救援过程中,基准计划不可避免地会发生调整, 而如何对基准计划进行调整即属于反应性调度的范畴. 现假定在反应性调度中,由于资源的限制, 各活动的开始时间不得早于其计划时间. 令救援活动$i$在执行过程中的实际工期为$d_i$ ($d_i$可视为随机变量$\tilde{d_i}$ (${\mu}_i$, ${\sigma}_i$)所形成总体中的一个样本),救援活动$i$ 的实际开始时间为$s_i$. 以活动$i$在应急计划中的开始时间$s_i^b$ 为基准,为其 定义一个权重系数${\omega}_i$, 用以测度$s_i$每延迟一个单位所造成损失的大小. ${\omega}_i$ 实质上反映了在反应性调度中各活动重要性次序,${\omega}_i$越大, 则活动的延迟损失也越大,越应该尽力保证其能够按计划开始. 在上述定义的基础上,将突发事件应急救援反应性调度问题定义为: 在给定应急基准计划和各活动权重系数的前提下, 基于活动的实际工期$d_i$确定其实际开始时间$s_i$, 以使由于活动开始时间延迟所引起的总损失最小化.
不难理解,在前摄性调度中救援期限$D$设置得越宽松, 则各活动上分配到的时间缓冲会越多, 因此越有能力吸收活动工期的随机变化, 进而减少在反应性调度中因活动开始时间延迟所引起的损失. 然而, 过度宽松的救援期限会降低应急基准计划的效率,延缓救援进程, 违背应急救援的基本原则. 反过来,如果为了追求效率, 在前摄性调度中将救援期限$D$设置得过紧,那么, 由于救援过程本身的不确定性, 应急基准计划在实施中便会发生大量的调整, 使得应急救援的组织和协调陷入混乱,反而导致救援效率的大幅下降. 所以,针对企业生产事故等突发事件的应急救援, 必须基于实际数据的统计及预测, 有效地协调前摄性调度与反应性调度之间的关系, 尽可能地实现二者的集成优化. 2 优化模型
根据上述对所研究问题的界定, 建立由前摄性和反应性两个子模型构成的突发事件应急救援调度集成优化模型, 表述如下.
前摄性调度优化模型 现假定在前摄性调度中, 基于活动工期均值${\mu}_i$将救援活动$i$ ($i=1, 2,\cdots,n$)的开始时间安排为$s_i^b$,则活动$i$ 所拥有的时间缓冲${\Delta}_i$ 可用下式计算:
$ {\Delta}_i=\min{(s_j^b)}-(s_i^b+{\mu}_i)\ \ \ \forall(i,j)\in A;\ \ \ i=1,2,\cdots,n. $
在救援过程中,如果活动$i$的实际工期$d_i$与${\mu}_i$发生偏离,只要其正的偏离幅度不超过 ${\Delta}_i$,则其紧后活动$j$的开始时间 $s_j^b$就无需进行延迟,从而确保基准计划实施的稳定性. 由于在$D$ 的约束下整个救援过程所拥有的总时间缓冲是有限的,为了将有限的时间缓冲合理地分配到各个活动上,基于工期标准差${\sigma}_i$为每个活动定义一个权重系数${\rho}_i$:$ {\rho}_i=\frac{{\sigma}_i}{\sum_{m=1}^{n}{\sigma}_m}, $
显然,${\rho}_i$ 越大,则活动的变化性越高, 其对基准计划的影响就越大. 所以, ${\rho}_i$也可理解为活动$i$上的单位时间缓冲对基准计划鲁棒性的贡献, 而时间缓冲${\Delta}_i$ 对基准计划鲁棒性的总贡献即为${\rho}_i{\Delta}_i$. 在此, 把整个基准计划的鲁棒性$Robu$ 定义为所有活动上时间缓冲的鲁棒性贡献的总和, 即$Robu=\sum_{i=1}^{n}({\rho}_i{\Delta}_i)$. 在上述讨论的基础上, 根据第1节中对所研究问题的界定, 建立突发事件应急救援的前摄性调度优化模型,表述如下:| \begin{equation} \mbox{Max} Robu=\sum_{i=1}^{n}{\rho}_i{\Delta}_i %max与s.t.是与公式不同的格式 \end{equation} | (1) |
| \begin{equation} \mbox{s.t.} s_1^b=0 \end{equation} | (2) |
| \begin{equation} s_i^b+{\mu}_i\le s_j^b \forall (i,j) \in A; i=1,2,\cdots,n \end{equation} | (3) |
| \begin{equation} s_n^b\le D \end{equation} | (4) |
| \begin{equation} \sum_{i \in P^t} {r_i^k}\le R^k t=0,1,\cdots,D; \quad k=1,2,\cdots,K \end{equation} | (5) |
| \begin{equation} s_i\mbox{为非负整数} i=1,2,\cdots,n \end{equation} | (6) |
反应性调度优化模型 由于救援活动$i$在执行过程中的实际工期$d_i$并不一定等于${\mu}_i$, 因而救援活动$i$ 的实际开始时间$s_i$可能会与其基准开始时间$s_i^b$ 不一致,亦即基准计划不可避免地会发生调整. 事实上, 在应急救援的实施过程中,各活动的工期是按照它们之间的逻辑关系, 依次由随机变量变成确定值的. 现假定在$T$时刻由于活动工期的变化, 不得不对基准计划进行调整. 将该时刻已经完成的活动集合定义为$F^T$, 正在进行的活动集合定义为$P^T$,尚未开始的活动集合定义为$U^T$. 定义该时刻活动的工期为$d_i^T$,对于$F^T$和$P^T$中的活动, 由于活动的实施已经变为现实,因此$d_i^T=d_i$; 对于$U^T$ 中的活动, 由于活动尚未开始,所以$d_i^T$ 仍取为$\tilde{d_i}$ 的均值${\mu}_i$, 即$d_i^T={\mu}_i$. 在上述讨论的基础上,根据第1节中对问题的界定, 可建立突发事件 应急救援的反应性调度优化模型表述如下:
| \begin{equation} \mbox{Min} Loss=\sum_{i=1}^{n}[{\omega}_i(s_i-s_i^b)] \end{equation} | (7) |
| \begin{equation} \mbox{s.t.} s_i=s_i^b i \in {F^T \cap P^T} \end{equation} | (8) |
| \begin{equation} s_j \ge s_i+d_i^T j\in U^T; \forall (i,j) \in A \end{equation} | (9) |
| \begin{equation} \sum_{i \in P^t} {r_i^k}\le R^k t=T,T+1,\cdots; \quad k=1,2,\cdots,K \end{equation} | (10) |
| \begin{equation} s_i\mbox{为非负整数} i=1,2,\cdots,n \end{equation} | (11) |
上述两个优化模型通过应急救援基准计划相关联,即前摄性调度优化模型生成内嵌有时间缓冲的活动基准开始时间,作为已知参数输入到反应性调度优化模型中,为活动实际开始时间的确定提供一个原始的基准. 在给定资源供给水平下,时间缓冲设置受到救援期限的限制,并决定了基准计划的鲁棒性高低,进而决定了反应性调度时基准计划可能的调整次数,以及每次调整时活动开始时间的延迟程度,最终决定了由于计划调整与活动延迟所引起的损失大小. 所以,通过上述两个模型对前摄性调度和反应性调度的集成优化,可以取得救援期限设定、计划鲁棒性水平及活动延迟损失控制之间的定量化协调与配合,确保救援目标的最有效实现. 3 禁忌搜索启发式算法
在上述前摄性和反应性调度优化模型中, 均存在着可更新资源约束(renewable resource constraint),所以, 它们可视为经典的资源约束项目调度问题RCPSP (resource-constrained project scheduling problem)在不同目标函数下的一种扩展. 由于RCPSP已被证明为NP-hard问题[11],因此, 本文所研究的问题也必然为NP-hard问题. 鉴于这一事实, 采用禁忌搜索启发式算法求解该问题. 之所以选择禁忌搜索, 是因为该种算法已被众多学者应用于各种调度问题的求解中, 且被证明为求解此类问题的最有效算法之一[12, 13, 14]. 下面首先针对前摄性调度优化模型设计禁忌搜索启发式算法, 随后说明如何对该算法进行调整,以求解反应性调度优化模型. 3.1 解的表示
基于所研究问题的特征,用如下两个列表表示问题的解:
● 活动次序列表$AL$: 该列表由$n$个活动代号构成, 各代号在列表中的位置即决定了其所对应活 动在计划安排时的优先次序. 基于$AL$,借助RCPSP中的SSGS (serial schedule generation scheme)[15], 便可将各活动安排在其满足资源及逻辑关系约束的最早时间开始, 从而生成一个可使救援过程尽早结束的基准计划.
● 时间裕量列表$SL$: 该列表由$n$个时间裕量${\varepsilon}_i \in [0, L_i-E_i$]构成,其中,$E_i$和$L_i$分别是活动$i$ 的最早和最晚开始时间,它们可基于活动网络及救援期限$D$通过CPM (critical path method)计算得到. 在编制基准计划时, ${\varepsilon}_i$ 被添加到相应的活动工期均值${\mu}_i$上,以便在 活动上形成所需的时间缓冲${\Delta}_i$. 注意,由于${\Delta}_i$ 是通过$s_i^b$ 的安排形成的,所以,${\varepsilon}_i$ 并不一定等于${\Delta}_i$.
给定一组$AL$和$SL$,基准计划可按照下述方式生成: 首先, 在$SL$所定义的${\varepsilon}_i$的基础上, 令${\mu}b_i={\mu}_i+{\varepsilon}_i$; 其次, 按照$AL$所定义的活动优先次序,基于${\mu}b_i$利用SSGS生成各 活动的开始时间,由此形成基准计划. 需要说明的是, 尽管${\varepsilon}_i$的取值被限制在[0,$L_i-E_i$]之内, 但上述解的表示方式仍有可能生成违反救援期限$D$ 约束的基准计划. 在算法的迭代过程中,当这种情况出现时,为使正常搜索不受影响, 算法不直接剔除不可行解而是将其目标函数惩罚为0. 在上述解的表示方式下,问题的初始可行解$(AL^{\rm ini},SL^{\rm ini})$可按照下述方式构造: 在不违反逻辑关系约束的前提下, 随机地给出一个活动次序列表$AL^{\rm ini}$; 同时, 在时间裕量列表$SL^{\rm ini}$上, 将所有的${\varepsilon}_i$都定义为0. 3.2 邻点生成机理
当前可行解$(AL^{\rm cur},SL^{\rm cur})$的邻点通过如下两个算子生成:
● 位置交换$(PS)$算子: 对于列表$AL^{\rm cur}$, 在不违反逻辑关系的前提下,选择两个活动并交换它们的位置, 从而生成当前解的一个邻点. 对列表$AL^{\rm cur}$上每一对满足上述条件的活动都独立地进行同样的处理, 由此得到一个邻点集合, 集合中每个邻点的$AL$列表上仅有两个位置与当前解不同.
● 裕量改变$(SC)$算子: 对于列表$SL^{\rm cur}$, 选择一个${\varepsilon}_i$并将其值改变为区间[0, $L_i-E_i$]中的另一值,从而生成当前解的一个邻点. 按照上述操作方式, 将所选择的${\varepsilon}_i$改变为区间[0, $L_i-E_i$]中的任何一个其他值,而且,对列表$SL^{\rm cur}$ 上除虚活动1 和$n$ 之外的每个${\varepsilon}_i$都独立地进行同样的处理, 由此得到一个邻点集合, 集合中每个邻点的$SL$列表上仅有一个${\varepsilon}_i$取值与当前解不同.
在由上述两个算子所得到邻点集合中, 选择目标函数值$Robu$最高的一个邻点记为$(AL^{\rm nei},SL^{\rm nei})$,将其作为算法迭代搜索的下一步移动方向. 3.3 禁忌列表及终止准则
对应于活动次序列表$AL$和时间裕量列表$SL$, 分别定义两个禁忌列表$TL^{AL}$和$TL^{SL}$,两个禁忌列表均采用 "先进先出FIFO (First-in-First-out)''的原则进行更新: 每当算法从当前解向选定的邻点移动时, 该移动的逆向移动从底部加入到禁忌列表中, 避免算法重新退回到当前解上; 与此同时, 最早进入列表的逆向移动从顶部移出列表, 列表中其余逆向移动向上递进一位. 所有位于禁忌列表中的逆向移动都是被禁止的,但是, 如果一个被禁止的逆向移动能够生成比当前最好解还要好的邻点时, 那么它的禁忌状态可以被激活,以使算法能够移动到该邻点上, 从而避免错失问题的最好解.
算法的终止准则设置为探测可行解的总数,即当算法搜索的可行解的总数达到某一设定值时,算法停止搜索并将保存的最好解输出为满意解. 3.4 搜索过程
由于问题的解由活动次序列表$AL$和时间裕量列表$SL$构成,所以, 采用两层禁忌搜索迭代嵌套的方式寻找问题的满意解. 内层迭代在给定的活动次序列表$AL$下搜索满意的时间裕量列表$SL^{\ast}$, 外层迭代在内层迭代返回的$SL^{\ast}$的基础上, 搜索满意活动次序列表$AL^{\ast}$. 为了便于算法的表述, 首先给出内层迭代Inner($AL$)的搜索步骤:
步骤1 输入初始$SL^{\rm ini}$及在$(AL,SL^{\rm ini})$下的目标函数值$Robu^{\rm ini}$. 定义内层迭代探测可行$SL$ 的总数$Num_{\rm stop}^{SL}$. 初始化禁忌列表$TL^{SL}$. 令内层迭代计数器$Num^{SL}=0$. 将当前解及当前最好解赋值为初始解: $SL^{\rm cur}=SL^{\rm ini}$,$Robu^{\rm cur}=Robu^{\rm ini}$; $SL^{\ast}=SL^{\rm ini}$,$Robu^{\ast}=Robu^{\rm ini}.$
步骤2 利用$SC$算子生成$SL^{\rm cur}$的一个邻点$SL^{\rm nei}$,计算在$(AL,SL^{\rm nei})$下的目标函数值$Robu^{\rm nei}$. 检查生成该邻点的移动是否位于禁忌列表$TL^{SL}$中,若是转步骤4; 否则,转步骤3.
步骤3 令$SL^{\rm cur}=SL^{\rm nei}$,$Robu^{\rm cur}=Robu^{\rm nei}$,$Num^{SL}=Num^{SL}+1$, 更新禁忌列表$TL^{SL}$. 如果$Robu^{\rm cur}> Robu^{\ast}$, 进一步令$SL^{\ast}=SL^{\rm cur}$,$Robu^{\ast}=Robu^{\rm cur}$, 转步骤5; 否则,直接转步骤5.
步骤4 如果$Robu^{\rm nei}>Robu^{\ast}$, 激活生成该邻点移动的禁忌状态,令$SL^{\rm cur}=SL^{\ast}=SL^{\rm nei}$,$Robu^{\rm cur}= Robu^{\ast}=Robu^{\rm nei}$, $Num^{SL}=Num^{SL}+1,$ 更新禁忌列表$TL^{SL}$,转步骤5; 否则, 转步骤2.
步骤5 判断$Num^{SL}$$\ge$$Num_{\rm stop}^{SL}$是否成立,若成立转步骤6; 否则,转步骤2.
步骤6 返回搜索到的满意$SL$及其对应的目标函数值, 即$SL^{\ast}$和$Robu^{\ast}$. 在Inner($AL$)的基础上,外层迭代可按下述步骤搜索问题的满意解:
步骤1 输入初始可行解$(AL^{\rm ini},SL^{\rm ini})$及其对应的目标函数值$Robu^{\rm ini}$. 定义外层迭代探测可行$AL$ 的总数$Num_{\rm stop}^{AL}$. 初始化禁忌列表$TL^{AL}$. 令外层迭代计数器$Num^{AL}=0$. 将当前解及当前最好解赋值为初始解: $AL^{\rm cur}=AL^{\rm ini}$, $SL^{\rm cur}=SL^{\rm ini}$,$Robu^{\rm cur}=Robu^{\rm ini}$; $AL^{\ast}=AL^{\rm ini}$,$SL^{\ast}=SL^{\rm ini}$, $Robu^{\ast}=Robu^{\rm ini}.$
步骤2 利用$PS$算子生成$AL^{\rm cur}$的一个邻点$AL^{\rm nei}$,调用Inner($AL^{\rm nei}$)并将返回的满意$SL$及其目标函数值记为$SL^{\rm nei}$和$Robu^{\rm nei}$. 检查生成该邻点的移动是否位于禁忌列表$TL^{AL}$ 中,若是转步骤4; 否则,转步骤3.
步骤3 令$AL^{\rm cur}=AL^{\rm nei}$,$SL^{\rm cur}=SL^{\rm nei}$,$Robu^{\rm cur}=Robu^{\rm nei}$, $Num^{AL}=Num^{AL}+1$,更新禁忌列表$TL^{AL}$. 如果$Robu^{\rm cur}> Robu^{\ast}$,进一步令$AL^{\ast}=AL^{\rm cur}$,$SL^{\ast}=SL^{\rm cur}$,$Robu^{\ast}=Robu^{\rm cur}$,转步骤5; 否则,直接转步骤5.
步骤4 如果$Robu^{\rm nei}>Robu^{\ast}$, 激活生成该邻点移动的禁忌状态,令$AL^{\rm cur}=AL^{\ast}=AL^{\rm nei}$,$SL^{\rm cur}=SL^{\ast}=SL^{\rm nei}$,$Robu^{\rm cur}= Robu^{\ast}=Robu^{\rm nei}$,$Num^{AL}=Num^{AL}+1,$ 更新禁忌列表$TL^{AL}$,转步骤5; 否则,转步骤2.
步骤5 判断$Num^{AL}$$\ge$$Num_{\rm stop}^{AL}$是否成立,若成立转步骤6; 否则,转步骤2.
步骤6 输出搜索到的满意解及其对应的目标函数值, 即$AL^{\ast}$、$SL^{\ast}$ 和$Robu^{\ast}$. 3.5 反应性调度优化模型的求解
需要特别说明的是, 上述算法是针对前摄性调度优化模型设计的. 算法通过如下调整后, 即可用于反应性调度优化模型的求解: 将目标函数由最大化$Robu$改为最小化$Loss$; 活动次序列表$AL$和时间裕量列表$SL$仅应用于集合$U^T$中的活动上, 在将$AL$ 和$SL$解码为救援计划时, 基于$F^T$和$P^T$中活动已经确定的开始时间,利用SSGS依次进行.
上述禁忌搜索算法采用Visual C++ 6.0语言编程,在CPU主频为1.6GHz、内存为768MB的个人计算机上运行. 禁忌列表的长度以及算法探测可行解总数通过实验法确定. 4 实际案例
用一个实际案例————KX 井喷事故的应急救援过程[16]对研究进行说明. KX井喷事故发生于 2003年12月23日,是中国石油天然气集团公司的一次代表性井喷事故. 通常, 井喷事故的应急救援过程包括事故报警及现场处置、救援资源调集、周边居民疏散及受害者搜救、事故现场监控及井喷处理、善后工作5个部分. 而一般事故造成的损失主要发生在点火之前,点火后井喷消失, 灾情得到极大缓解. 因此, 本文将研究重点限定于事故发生到点火之间的应急救援过程,图 1 以AoN网络的形式给出了各救援活动之间的逻辑关系.
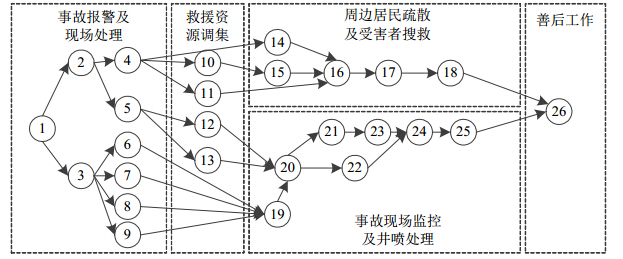 |
| 图 1 救援活动的AoN网络图 |
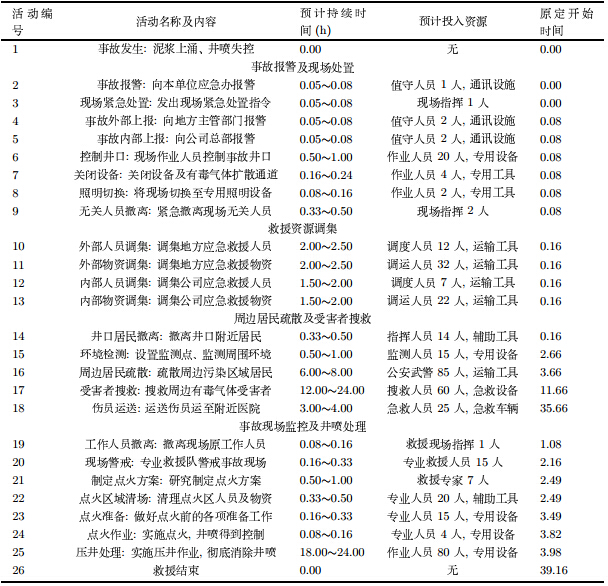
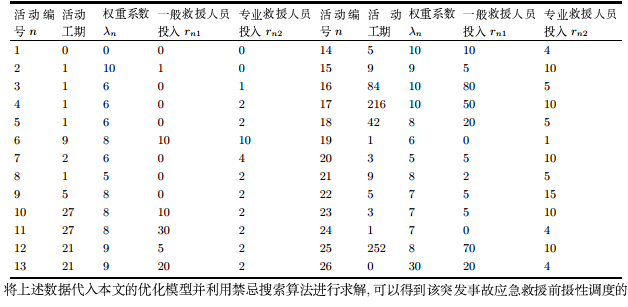
根据石油天然气行业应急管理的要求,相关单位根据气井所在地区井喷事故的历史数据以及该气井勘探情况,综合考虑企业的技术实力和当地政府的应急救援能力,对一旦发生井喷事故时,各救援活动的预计持续时间及投入资源进行了估算,结果列于表 1中. 同时,按照总救援时间最短的原则给出了原定的应急救援计划. 对表 1中数据进行整理,将活动工期的期望值取做预计持续时间的平均值,单位调整为按5分钟计算. 此外,由于此次事故主要是毒气泄露,因而活动权重根据该活动每延误一个时间单位对人员所造成的伤害程度进行估算,得到结果列于表 2中. 在应急救援过程中,将一般救援人员的可用量设定为150,专业救援人员的可用量设定为30,救援期限取为关键路径的1.3倍.
将上述数据代入本文的优化模型并利用禁忌搜索算法进行求解, 可以得到该突发事故应急救援前摄性调度的基准计划如下: $S=(0,0,0,1,1,1,1,1,1,2,2,2,2,2,29,139,226,442,202,203,206,206,234,237,238,490)$. 在该计划下的活动缓冲为: $\Delta_5=192$,$\Delta_{14}=101$, $\Delta_{15}=3$,$\Delta_{20}=19$,其余活动为0, 计划的鲁棒性$Robu=65.538$. 而表 1中所给出的原定应急救援计划为: $S=(0,0,0,1,1,1,1,1,1,2,2,2,2,2,29,38,122,388,10,23, 26,26,35,38,39,380)$,其鲁棒性$Robu=7.33152$. 由此可见, 与原定的救援计划相比, 前摄性调度方法得到的救援计划的鲁棒性提高了约794%.
在项目实施过程中,两种资源使用量的变化情况如图 2和图 3(图中, 资源1和资源2分别代表一般救援人员和专业救援人员)所示. 由图可见, 两种资源使用量均未超出资源可用量的限制. 其中, 专业救援人员在整个计划过程中基本上保持均衡, 而在最为紧迫的搜救时段$t$=206$\sim$210,使用量达到最大值25; 一般救援人员在$t$=29$\sim$137 时段都保持较低水平15, 而在疏散周围人员与搜救中毒人员时段$t$=238$\sim$441, 由于救援的范围大,需要投入大量的一般性救援人员, 所以该时段的此类资源的使用量达到最大值120.
 |
| 图 2 资源1使用量变化情况 |
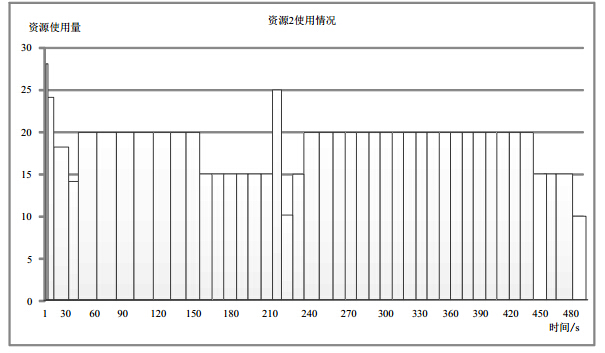 |
| 图 3 资源2使用量变化情况 |
在实际救援过程中,由于活动工期的随机变化,必然会使基准计划的执行发生调整. 该井喷事故的应急救援在实际执行中即发生了如下与计划不符的变化:
● 救援活动4 "事故外部上报"持续时间0.93小时, 比计划长0.85小时.
● 救援活动6 "井口控制''持续时间0.43小时,比计划短0.57小时.
● 救援活动12 "内部人员调集''持续时间2.43,比计划长0.43小时.
● 救援活动16 "周边居民疏散''持续时间9.67小时,比计划长1.67小时.
● 救援活动21 "制定点火方案''持续时间4小时,比计划长3小时.
● 救援活动24 "点火作业''持续时间0.67小时,比计划长0.51小时.
基于上述的随机变化,调用本文所构建的反应性调度模型对基准计划进行调整,得到的结果如表 3 所示. 由表 3可见,基准计划总共调整4次,损失值合计为 1844. 作为对比,若按照原定的应急救援计划进行反应性调整,则得到的结果见表 4. 由表 4 可见,基准计划需要调整 5 次,损失值合计为2956. 上述结果表明,采用本文所提出的方法对该事故的救援过程进行调度,可以有效降低基准计划调整所造成的损失,降幅达到60.3%.
上述结果的原因可以解释如下: 与救援时间最短的原定基准计划相比,鲁棒性最大的基准计划根据活动工期的随机变化性,适度地加入了一定的时间缓冲,从而对基准计划起到了有效的保护作用,提高了计划的鲁棒性并同时减少了调整所造成的损失. 但需要指出的是,鲁棒性的提高是有代价的,它使得应急救援的总时间有所延长: 鲁棒性最大的基准计划总救援时间为515,比原定基准计划的总救援时间494多了21个单位. 所以,在实际突发事故的应急救援中,基准计划鲁棒性高低的设置需要决策者慎重的考虑和权衡.
此外,从基准计划的调整过程还可以看出,反应性调度是一个动态过程,而且随着应急救援的推进,反应性调度时发生调整的活动数目会逐渐减少. 例如,在鲁棒性最大基准计划的调整过程中,第1次有4个活动发生调整,第2次为3个,第3次为4个,最后一次为2个; 而在救援时间最短基准计划的调整过程中,第1次有8个活动发生调整,第2次为6个,第3、4次均为3个,最后一次为1个. 这现象主要是由于活动之间的逻辑关系所造成的: 前期调整的活动一般位于AoN网络的前端,其后面跟有较多的尚未执行的后续活动,因此,此时的调整容易引起连锁反应,导致后续活动的时间安排随之同步发生调整; 相反,后期调整的活动通常位于AoN网络的后端,其后尚未执行的活动数目较少,所以,它们的调整造成的影响范围则较小,因而反应性调度时发生调整的活动数目相应就较少.
最后,将前摄性调度算法与反应性调度算法分别运行50次, 可以得到一组不同的鲁棒性与损失值之间变化关系的有趣结果(如图 4所示):当鲁棒值从61.8043变化到70.9948之间时, 损失值先下降而后上升,如此循环波动并沿着上升的总趋势向前发展; 在鲁棒值取为63.2228与65.538时,损失值达到两个极小值1944和1844; 随着鲁棒性继续上升到70$\sim$72之间时, 反应性调度的损失值稳定在2880左右, 接近于救援时间最短基准计划的损失值2956. 以上结果表明, 并不是基准计划的鲁棒值越高,反应性调度中的损失值就越小, 两者并不存在一个绝对的单调关系,可以通过反复多次的求解运算, 找到二者之间的平衡点,在保持前摄性调度鲁棒性较高的前提下, 获得较小反应性调度的损失值,达到两种调度方式的集成优化, 获得突发事件应急救援的最佳结果.
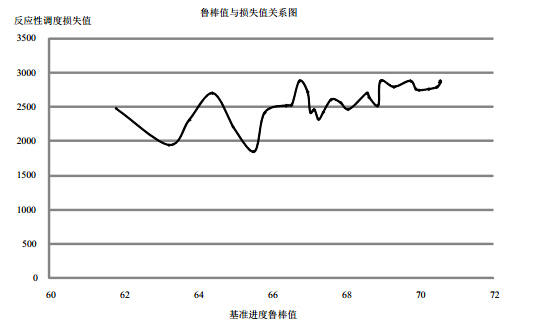 |
| 图 4 鲁棒值与损失值关系图 |
本文针对企业生产事故等突发事件的应急救援过程, 研究了前摄性调度与反应性调度的集成优化问题. 首先, 对所研究问题进行界定, 分别构建了基于鲁棒性最大的前摄性调度优化模型与损失值最小的反应性调度优化模型. 在前摄性调度模型中,借助随机活动工期的方差值, 为每个活动定义一个权重因子以反映活动的变化性程度; 而鲁棒性则定义为所有活动上的时间缓冲的鲁棒性贡献值总和; 目标是在救援期限与可更新资源约束条件下, 寻求鲁棒性最大化的应急救援基准计划. 在反应性调度模型中, 由于活动工期的变化性,忽略了救援期限的限制, 目标为最小化调整后的计划偏离基准计划的损失值. 其次, 根据问题的强NP- hard属性,分别针对前摄性调度模型和反应性调度模型, 设计了双环路禁忌搜索启发式算法, 通过对顺序列表与裕量列表的迭代搜索, 算法在可行邻域内寻找问题的满意解. 最后, 通过一个井喷事故应急救援实际案例对研究进行说明, 给出了该实际案例的满意的前摄性调度基准计划与反应性调度调整方案, 并结合实际情况对求解结果进行深入的讨论分析,得出如下结论: 利用本文方法所得到的基准计划的鲁棒性远远大于救援时间最短的基准计划, 同时反应性调度中的调整损失值也相对较小; 随着应急救援的向前推进, 反应性调度时发生调整的活动数目会逐渐减少; 随着前摄性调度的鲁棒性上升,反应性调度的损失值会先下降再上升, 如此循环并趋于一个稳定值,因而可通过反复多次的求解运算, 找到二者之间的平衡点,实现两种调度方式的集成优化. 本文的研究可为突发事件应急救援的计划制定与实时的动态调整提供定量化决策支持.
| [1] | 翟晓敏, 盛昭瀚, 何建敏. 应急研究综述与展望[J]. 系统工程理论与实践, 1998, 18(7): 80-87.Zhai Xiaomin, Sheng Zhaohan, He Jianmin. Recent developments of emergency study[J]. Systems Engineering——Theory & Practice, 1998, 18(7): 80-87. |
| [2] | 曹杰, 杨晓光, 汪寿阳. 突发公共事件应急管理研究中的重要科学问题[J]. 公共管理学报, 2007, 4(2): 84-95.Cao Jie, Yang Xiaoguang, Wang Shouyang. Key scientific problems in public emergency management[J]. Journal of Public Management, 2007, 4(2): 84-95. |
| [3] | 国务院应急管理办公室. 国家突发公共事件总体应急预案[EB/OL]. [2013-08-08]. http://www.china.com.cn/chinese /law/1086058.htm. |
| [4] | 佘廉, 吴国斌, 吕浩. 关于我国政府对重大突发事件管理现状的问卷调查与分析[J]. 中国安全科学学报, 2005, 15(7): 16-20.She Lian, Wu Guobin, Lü Hao, et al. Analysis on questionnaire investigation of the current government management status during severe accidental emergency in China[J]. China Safety Science Journal, 2005, 15(7): 16-20. |
| [5] | Lambrechts O, Demeulemeester E, Herroelen W. A tabu search procedure for developing robust predictive project schedules[J]. International Journal of Production Economics, 2008, 111(2): 493-508. |
| [6] | Van de Vonder S, Demeulemeester E, Herroelen W. Proactive heuristic procedures for robust project scheduling: An experimental analysis[J]. European Journal of Operational Research, 2008, 189(3): 723-733. |
| [7] | Van de Vonder S, Ballestin F, Demeulemeester E, et al. Heuristic procedures for reactive project scheduling[J]. Computers & Industrial Engineering, 2007, 52(1): 11-28. |
| [8] | Deblaere F, Demeulemeester E, Herroelen W. Reactive scheduling in the multi-mode RCPSP[J]. Computers & Operations Research, 2011, 38(1): 63-74. |
| [9] | Lambrechts O, Demeulemeester E, Herroelen W. Proactive and reactive strategies for resource-constrained project scheduling with uncertain resource availabilities[J]. Journal of Scheduling, 2008, 11(2): 121-136. |
| [10] | Elmaghraby S E. Activity nets——A guided tour through some recent developments[J]. European Journal of Operational Research, 1995, 82(3): 383-408. |
| [11] | Blazewicz J, Lenstra J K, Kan A. Scheduling subject to resource constraints——Classification and complexity[J]. Discrete Applied Mathematics, 1983, 5(1): 11-24. |
| [12] | Waligora G. Discrete-continuous project scheduling with discounted cash flows——A tabu search approach[J]. Computers & Operations Research, 2008, 35(7): 2141-2153. |
| [13] | Mika M, Waligora G, Weglarz J. Simulated annealing and tabu search for multi-mode resource-constrained project scheduling with positive discounted cash flows and different payment models[J]. European Journal of Operational Research, 2005, 164(3): 639-668. |
| [14] | Mika M, Waligora G, Weglarz J. Tabu search for multi-mode resource-constrained project scheduling with schedule-dependent setup times[J]. European Journal of Operational Research, 2008, 187(3): 1238-1250. |
| [15] | Kolisch R. Serial and parallel resource-constrained project scheduling methods revisited: Theory and computation[J]. European Journal of Operational Research, 1996, 90(2): 320-333. |
| [16] | 中国石油天然气集团公司工程技术与市场部. 中国石油天然气集团公司井喷事故案例汇编[M]. 北京: 石油工业出版社, 2006. |