0 引言
石油、化工、冶金、造纸、制糖、医药制剂等流程工业生产的显著特点,是连续性的生产过程,即物料连续不断地输入或输出设备,通过化 学反应或物理处理改变形状或属性. 以往,流程工业大多采用单一品种大量生产方式. 随着顾客需求日益多样化和个性化,现代流程工 业已开始转向广泛采用多品种成批轮番生产. 流程式的多品种成批轮番生产与以往单一品种大量生产相比较,存在着许多不同: 一是计 划期内要生产出多种产品而非一种产品,多种产品通常要共用一系列生产装置; 二是多种产品要在共用生产装置上组织成批轮番生产,而 同种产品相同批连续性加工,同批内物料不可分离和间断,这里的批是指在同一生产装置上使用同一生产配方在同一作业条件下被加工对 象的集合或总量; 三是多品种成批轮番生产中品种切换时,不仅有生产调整准备时间损失,而且还有物料损失,即输入物料并非百分之百 地转化为有效输出,生产过程各阶段都存在物料转化率的问题; 四是每种产品分批的批量大小又受到中间库存的约束. 由于存在着这些差 异和不同,使得流程工业企业由单一品种大量生产转向多品种成批轮番生产时,在其生产的计划、调度与控制上面临着诸多比以往更加 复杂而又急需解决的新难题.
然而,迄今为止,流程式多品种成批轮番生产的计划与调度问题仍然是制造性生产管理研究上探索较少的一个 领域,尤其是对多品种成批轮番地经过多阶段生产、共享装置(设备)、具有物料变动转化率和中间库存约束的分批计划与 调度问题,尚缺少适用有效的方式方法和手段[1]. 至今已有研究工作和成果主要集中在分批次数(批次)或每批数量(批量)固定 情形下,考虑三个生产阶段内的生产调度问题[2, 3, 4, 5, 6, 7]. 在围绕这些调度问题的求解方法上,以往文献主要是构造混合整数线性规 划模型和启发式算法[8, 9, 10, 11, 12, 13, 14, 15, 16, 17]. 但是,这些方法对求解大规模问题很难在有效时间内获得较好解,解的质量很难保证,而且问题的 微小变化也可能使算法失效.
本文紧密结合流程式多品种成批轮番生产实际环境及管理需求,在计划与调度决策方面考虑分批和调度的集成,采用连续 时间建模策略建立流程式多品种成批轮番生产的分批和调度集成决策的混合整数规划模型,并给出相应的求解策略和算法,旨在拓 展流程式多品种成批轮番生产分批及调度理论方法,为流程工业企业多品种成批轮番生产管理实践提供理论依据和方法支持. 1 问题描述及建模 1.1 问题描述
给定$p$种产品$P=\{1,2,\cdots,p\}$, 每种产品生产都要依次经过$r$个生产阶段$R=\{1,2,\cdots,r\}$. 产品$i \in P$的需求量记为$D_{i}$. 物料在各个阶段上进行化学反应, 反应物按照转化率得到生成物, 因此产品在各个阶段上的生产量不完全相等. 由于多种产品需要共用生产设备, 每种产品的需求量通常又都大于各阶段上设备的单次生产批量, 因此产品在各个阶段上都需要进行分批生产. 考虑到批量大小及品种切换次数对生产经济性和安全性的影响, 实际生产中一般都规定每次加工批量的下限和上限. 令$B^{ \max}_{ij}$和$B^{ \min}_{ij}$分别表示产品$i$在阶段$j$上的最大和最小生产批量. 由此, 流程式多品种成批轮番生产面临的第一层决策问题就是分批, 即确定产品$i$在阶段$j$ 上的批次和批量.
产品$i \in P$的一个批次在阶段$j \in R$上的生产时间包括两部分, 一部分是该批的额定加工时间$\alpha_{ij}$, 另一部分是与批量大小呈线性关 系的生产准备时间,记$\beta_{ij}$ 为与批量大小相关的生产准备时间系数. 如果在同一阶段$j \in R$上前后两个批是分别加工不同 的产品$i$和$i'$, 则需要有一个调整时间$\tau_{ii'j}$ 来清理设备(如化工反应器). 此外,对于流程式生产中的同一种产 品$i$,在其相邻两个生产阶段$j$ 和$j+1$之间都配置有存储设备,用以临时存储半成品和起到库存缓冲作用, 记存储设备的最大库 存能力为$E^{\max}_{ij}$. 由此, 流程式多品种成批轮番生产面临的第二层决策问题就是批调度, 即在满足设备能力、产品供料 关系和中间库存能力等约束条件下, 确定在每一阶段上不同产品各个批的开始加工时间. 1.2 数学模型
针对流程式多品种成批轮番生产同时面临分批和批调度的双层决策问题, 本文通过引入批及其在各阶段加工位置之间的分配关系来处理分批决策问题, 进而通过引入连续时间变量来处理批调度决策问题. 定义$Q_{ij}$产品$i$在阶段$j$上的需求量, 考虑到生产经济性、安全性和尽可能减少调整准备时间损失, 产品$i$在阶段$j$上的分批数显然在集合$\{\lceil Q_{ij}/B^{\max}_{ij} \rceil,\lceil Q_{ij}/B^{\max}_{ij} \rceil+1,\cdots,\lceil Q_{ij}/B^{\min}_{ij} \rceil \}$ 内. 这里,阶段$j$ 上最大的分批数为$\sum\limits_{i \in P} \lceil Q_{ij}/B^{\min}_{ij} \rceil $,所有阶段上最大可能分批数$n=\max\limits_{j \in R} \sum\limits_{i \in P} \lceil Q_{ij}/B^{\min}_{ij} \rceil $.为了建模需要,在任意阶段$j$上,可预先设定$n$个位置, 每个位置可能对应一个分批,称为实位,有些位置可能不对应任何分批, 称为空位. 令$N= \{1,2,\cdots,n \}$为预定位置集合.
定义$w_{ijk}=1$表示产品$i \in P$的一个分批被分配到阶段$j \in R$上的第$k \in N $个位置上,否则$w_{ijk}=0$. $b_{ijk}$表示 产品$i \in P$ 的被分配到阶段$j \in R$ 上的第$k \in N$个位置上的反应物批量,$y_{ijk}$表示生成物批量,$ b_{ijk}$ 与$y_{ijk}$的比值 是转化率,令$\delta^{\max}_{ij} $ 和$\delta^{\min}_{ij} $分别表示最大和最小转化率,$ z_{ijk}$表示$b_{ijk}$ 与$y_{ijk}$的差. $ts_{ijk}$表 示产品$i \in P$的被分配到阶段$j \in R$上的第$k \in N$个位置上的批开始加工时间, $E_{ijkk'}$表示产品$i$ 在阶段$j$的位置$k$加工完 输出物料,在阶段$j+1$的位置$k'$开始加工输入物料后的中间量, $h_{ijkk'}$表示中间量是否为非负,$g_{ijkk'}$表示中间量是否 不大于最大库存能力. $H$表示展望期,$A$为极大的正数, $B$为极小的正数. 设以最小化最大完工时间$F$为目标, 建立分批和调度集成决策 的混合整数规划模型如下: \begin{eqnarray} % \nonumber to remove numbering (before each equation) {\rm Min}~F=\max \{ts_{irn} + \alpha_{ir} w_{irn} + \beta_{ir} y_{irn}|i \in P \} \end{eqnarray}
(1) \begin{eqnarray} % \nonumber to remove numbering (before each equation) b_{ijk}=y_{ijk}+z_{ijk} , ~~~~\forall i \in P,j \in R,k \in N \end{eqnarray}
(2) \begin{eqnarray} % \nonumber to remove numbering (before each equation) \delta^{\min}_{ij} b_{ijk}\leq y_{ijk}\leq\delta^{\max}_{ij} b_{ijk},~~~~\forall i \in P,j \in R,k \in N \end{eqnarray}
(3) \begin{eqnarray} % \nonumber to remove numbering (before each equation) (1-\delta^{\max}_{ij}) b_{ijk}\leq z_{ijk}\leq(1-\delta^{\min}_{ij}) b_{ijk} ,~~~~\forall i \in P,j \in R,k \in N \end{eqnarray}
(4) \begin{eqnarray} % \nonumber to remove numbering (before each equation) w_{ijk} B^{\min}_{ij}\leq b_{ijk}\leq w_{ijk} B^{\max}_{ij}, ~~~~\forall i \in P,j \in R,k \in N \end{eqnarray}
(5) \begin{eqnarray} % \nonumber to remove numbering (before each equation) \sum_{i \in P}w_{ijk}\leq1,~~~~\forall j \in R,k \in N \end{eqnarray}
(6) \begin{eqnarray} % \nonumber to remove numbering (before each equation) \sum_{i \in P}w_{ijk}\geq\sum_{i \in P}w_{ij,k+1} ,~~~~\forall j \in R,k \in N:k\neq n \end{eqnarray}
(7) \begin{eqnarray} % \nonumber to remove numbering (before each equation) \sum_{k \in N}y_{ijk}=\sum_{k \in N}b_{i,j+1,k},~~~~\forall i \in P,j \in R:j \neq r \end{eqnarray}
(8) \begin{eqnarray} % \nonumber to remove numbering (before each equation) \sum_{k \in N}y_{irk}=D_{i},~~~~\forall i \in P \end{eqnarray}
(9) \begin{eqnarray} % \nonumber to remove numbering (before each equation) E_{ijkk'}=\sum_{0\leq d\leq k}y_{ijd}-\sum_{0\leq d\leq k'}b_{i,j+1,d} ,~~~~\forall i \in P,j \in R:j \neq r,k \in N,k' \in N \end{eqnarray}
(10) \begin{eqnarray} % \nonumber to remove numbering (before each equation) (h_{ijkk'}-1)A\leq E_{ijkk'}\leq h_{ijkk'}A+(h_{ijkk'}-1)B, ~~~~\forall i \in P,j \in R:j \neq r,k \in N,k' \in N \end{eqnarray}
(11) \begin{eqnarray} % \nonumber to remove numbering (before each equation) (g_{ijkk'}-1)A\leq (E^{\max}_{ij}-E_{ijkk'})\leq \end{eqnarray} \begin{eqnarray} g_{ijkk'}A+(g_{ijkk'}-1)B,~~~~ \forall i \in P,j \in R:j \neq r,k \in N,k' \in N \end{eqnarray}
(12) \begin{eqnarray} % \nonumber to remove numbering (before each equation) ts_{ij,k+1}\geq ts_{ijk}+\alpha_{ij} w_{ijk} + \beta_{ij} y_{ijk},~~~~ \forall i \in P,j \in R,k \in N:k \neq n \end{eqnarray}
(13) \begin{eqnarray} % \nonumber to remove numbering (before each equation) ts_{ij,k+1}\geq ts_{i'jk}+\alpha_{i'j} w_{i'jk} + \beta_{i'j} \end{eqnarray} \begin{eqnarray} y_{i'jk}-H(1-w_{i'jk})+\tau_{ii'j}w_{ij,k+1},~\forall i \in P,i' \in P,j \in R,k \in N:k \neq n \end{eqnarray}
(14) \begin{eqnarray*} % \nonumber to remove numbering (before each equation) ts_{i,j+1,k'}+H(1-w_{i,j+1,k'})+Hh_{ij,k-1,k'}+H(1-h_{ijkk'})\geq \end{eqnarray*} \begin{eqnarray*} ts_{ijk}+\alpha_{ij} w_{ijk} + \beta_{ij} y_{ijk}-H(1-w_{ijk}), \end{eqnarray*}
(15) \begin{eqnarray} % \nonumber to remove numbering (before each equation) \forall i \in P,j \in R:j \neq r,k \in N,k' \in N \end{eqnarray}
(16) \begin{eqnarray*} \beta_{ij} y_{ijk}+H(1-w_{ijk})+Hg_{ij,k,k'-1}+H(1-g_{ijkk'}), \end{eqnarray*} \begin{eqnarray*} \beta_{ij} y_{ijk}+H(1-w_{ijk})+Hg_{ij,k,k'-1}+H(1-g_{ijkk'}), \end{eqnarray*}
(17) \begin{eqnarray} % \nonumber to remove numbering (before each equation) \forall i \in P,j \in R:j \neq r,k \in N,k' \in N \end{eqnarray}
(18) \begin{eqnarray} % \nonumber to remove numbering (before each equation) ts_{ijk}\leq H,~~~~~~~~\forall i \in P,j \in R,k \in N \end{eqnarray}
(19) \begin{eqnarray} % \nonumber to remove numbering (before each equation) ts_{ijn}+\alpha_{ij} w_{ijn} + \beta_{ij} y_{ijn}\leq H,~~~~ \forall i \in P,j \in R \end{eqnarray}
(20) \begin{eqnarray} % \nonumber to remove numbering (before each equation) \sum_{i \in P}\sum_{k \in N}(\alpha_{ij} w_{ijk} + \beta_{ij} y_{ijk})\leq H,~~~~\forall j \in R \end{eqnarray}
(21)
2 模型求解的启发式粒子群算法(SPSO) 2.1 粒子群(PSO)算法由PSO算法生成$q$个粒子,粒子由位置和速度两种向量组成,速度向量表示粒子搜索的方向和步长,位置向量与问题的决策变量 对应,可以解码为问题的可行方案. 位置向量参照两个最好位置进行自我调整: 一个是粒子自身搜索到的最好位置,表示到当前代数 为止粒子找到的最好解; 另一个是$q$个粒子整体搜索到的最好位置,表示到当前代数为止种群找到的最好解. 评价粒子位置好坏用问题的目标函数衡量.
假设$m$维空间,问题解的构成可以用$m$维向量表示. 在算法的每一代, 粒子$u$自身找到的当前最好位置为$P_{u}=(p_{u1},p_{u2},\cdots,p_{um}) $,整个种群找到的当前最好位置为$G=(g_{1},g_{2},\cdots,g_{m}) $. 如果用向量$X_{u}=(x_{u1},x_{u2},\cdots,x_{um}) $和$V_{u}=(v_{u1},v_{u2},\cdots,v_{um}) $分别表示粒子$u$在算法的位置和速度, 下面两个等式描述了粒子速度与位置向量的更新过程: \begin{eqnarray*} % \nonumber to remove numbering (before each equation) v_{ui}'=wv_{ui}+c_{1}r_{1}(p_{ui}-x_{ui})+c_{2}r_{2}(g_{i}-x_{ui}), \end{eqnarray*} \begin{eqnarray*} % \nonumber to remove numbering (before each equation) x_{ui}'=x_{ui}+v_{ui}'. \end{eqnarray*} 其中,$w$为惯性系数; $c_{1}$和$c_{2}$为正的系数,是加速因子, 用来改变粒子追随自己最好位置和整体最好位置的寻优 方向时的移动距离, 合适的加速因子值可以实现增加算法的收敛速度同时跳出局部最优限制, 一般取$w$为$1$,$c_{1}$、 $c_{2}$为$2$. $ r_1$和$r_{2}$是$ [0, 1]$之间服从均匀分布的两个独立随机数. 算法的停止准则为最大的迭代次数或整体最好的位置达到指定值. 2.2 粒子的编码
对流程式多品种轮番生产分批和调度集成决策的混合整数规划模型的求解, 需要一并确定出每种产品的批次、批量、转化率以及在各阶段(设备)上的生产排序和开始生产时间. 为此,以$x_{ulk}$ 表示第$u$个粒子的批量和转化率. 定义$E =\{1,2, \cdots,e\}$为任务集合,$l \in E$,$l$的取值由产品$i$ 和阶段$j$ 决定,$l=i+p(j-1)$,$e= pr$; $k$的取值分为两部分:当$k\leq n$ 时, $x_{ulk}$表示批量; 当$ n<k\leq 2n$时,$x_{ulk}$表示转化率. 由于每个阶段上的一个位置只能生产一批产品,因而粒子$u $在位置$k$上的变量集合$B=\{x_{ulk}|l=1+p(j-1),\cdots,pj\}$, 且$B$中只能有一个非$0$变量. 为满足该限制条件, 这里采用如下修复策略:
Step 1 随机生成各产品的选择概率.
Step 2 比较概率,记录最大概率的产品编号$g$.
Step 3 集合$B$中$l\neq g$时,$x_{ulk}=0$.
此外,变量取值上须符合生产量和需求量之间的逻辑关系: 某阶段需要的输入物料量等于其之前阶段的批量与转化率乘积的总和; 因最后阶段生 产结束时不存在中间库存,所以最后阶段$r$的输出量等于相应产成品的需求量. 基于这种逻辑关系,提出以下批量修复策略:
Step 1 $l$表示产品和设备两种信息,$E_{l}$ 表示$l$的加工总量,$S_{l}$ 表示$l$的输出总量,$ D_{i} $表示产品$i $的需求量. 初始化这些变量,$ S_{l}$ 为$0$,$ D_{i}$根据实际需求量给出.
Step 2 令$j=r$.
Step 3 阶段$r$产品$i$的输出总量: $S_{l}=S_{i+p(r-1)}=\sum\limits_{k=1,2,\cdots,n}x_{u,i+p(r-1),k}x_{u,i+p(r-1),n+k}$.
Step 4 比较输出总量与需求量, 根据比较结果采用两种方式修复. 当输出总量大于需求总量,从$n$ 开始减少不为$0$的批,直到输出总量等于需求量. 当输出总量大于需求总量,从$n$ 开始减少不为$0$的批, 直到输出总量等于需求量. 当输出总量小于需求总量,从后向前增加为$0$ 的批,增加后的批量不能超过最大批量限制,直到输出总量与需求量相等.
Step 5 令$j=j-1$, 计算阶段$j$的输出量和需求量$S_{l}=S_{i+p(j-1)}=\sum\limits_{k=1,2,\cdots,n}x_{u,i+p(j-1),k}x_{u,i+p(j-1), n+k}$,$D_{i}=E_{i+pj}=\sum\limits_{k=1,2,\cdots,n}x_{u,i+pj,k}$. 比较输出量与需求量,根据比较结果修复.
Step 6 当$j>1$时,循环Step $5\sim6$, 完成所有产品在各阶段设备批量修复. 当$j=1$时,转到Step 7.
Step 7 结束. 2.3 单纯形搜索
由粒子群中各粒子的当前解可构成单纯形序列. 集合$SM$由$q$个不同的顶点组成$SM=\{X_{u}|u=1,2,\cdots,q\}$, $X_{u}$表示第$u$个顶点位置向量. 序列$\sum=(\sum_{1},\sum_{2},\cdots,\sum_{q})$ 表示目标函数值由小到大将顶点排序. 单纯形搜索通过反射、扩张和收缩等方法反复替换顶点, 直到满足停止准则跳出循环,得到更新的解. 这样搜索不仅能够加快对最优解的趋近, 还可跳出局域范围而增加得到最优解的可能性. 搜索流程如下:
Step 1 设置算法参数,反射系数$a(a\geq 1)$, 扩展系数$b(b\geq 1)$,正向收缩系数和反向收缩系数$d(0\leq d\leq 1)$、$g(0\leq g\leq1)$. 本文参照一般参数值, 取$a=1.0,~b=2.0,~d=0.5,~g=0.5$.
Step 2 获得$q$个单纯形的初始顶点, 建立集合$SM=\{X_{u}|u=1,2,\cdots,q\}$, 并计算$X_{u}$的目标函数值$y_{u}$.
Step 3 按升序排列目标函数值$y_{u}$,得到排序$\sum$, 表示顶点排序.
Step 4 计算集合$SN=\left\{X_{u}|X_{u}\in SM,u\neq \sum_{1}\right\}$中所有位置点的重心$X^{z}$. $SN$ 集合是在顶点集合$SM$中去除掉最好目标函数值的位置点, 该点是排序中第$1$个顶点. 重心按照如下公式计算: \begin{eqnarray*} % \nonumber to remove numbering (before each equation) x^{z}_{lk}=\sum_{X_{u}\in SN}x_{ulk}y_{u}\left/\sum_{X_{u}\in SN}y_{u}.\right. \end{eqnarray*}
Step 5 定义$5$个位置向量, 分别为新位置$X^{d}_{1}$、反射位置$X^{d}_{2}$、扩张位置$X^{d}_{3}$、正向收缩位置$X^{d}_{4}$、反向收缩位置$X^{d}_{5}$.
Step 6 计算反射向量$X^{d}_{2}$, 反射向量是以$X^{z}$为中心, 对顶点集合$SM$中最差目标函数值的位置点$X_{\sum_{q}}$进行反射$X^{d}_{2}=X^{z}+a(X^{z}-X_{\sum_{q}})$.
Step 7 计算反射向量$X^{d}_{2}$的目标函数值$Y^{d}_{2}$, 比较$Y^{d}_{2}$与集合$SM$中最好目标函数值$y_{ \sum_{1}}$. 如果反射向量的目标函数值$y^{d}_{2}$小于$y_{\sum_{1}}$,向下执行. 否则,转到Step $10$.
Step 8 计算扩张向量$X^{d}_{3}=X^{z}+b(X^{z}-X_{\sum_{q}})$.
Step 9 计算扩张向量$X^{d}_{3}$的目标函数值$y^{d}_{3}$, 比较$y^{d}_{3}$与$y^{d}_{2}$. 如果$y^{d}_{3}<y^{d}_{2}$, $X^{d}_{1}= X^{d}_{3}$; 否则$X^{d}_{1}= X^{d}_{2}$. 转到Step $16$.
Step 10 对于$y^{d}_{2}$大于$y_{\sum_{1}}$的情况, 如果$y^{d}_{2}$小于$y_{\sum_{q}}$,向下执行; 否则转到Step $13$.
Step 11 计算正向收缩向量$X^{d}_{4}=X^{z}+d(X^{z}-X_{\sum_{q}})$.
Step 12 计算正向收缩向量$X^{d}_{4}$的目标函数值$y^{d}_{4}$, 比较$y^{d}_{4}$与$y^{d}_{2}$. 如果$y^{d}_{4}<y^{d}_{2}$, $X^{d}_{1}= X^{d}_{4}$,否则$X^{d}_{1}= X^{d}_{2}$. 转到Step $16$.
Step 13 当$y^{d}_{2}$大于$y_{\sum_{q}}$时, 计算反向收缩向量$X^{d}_{5}=X^{z}-d(X^{z}-X_{\sum_{q}})$.
Step 14 计算反向收缩向量$X^{d}_{5}$的目标函数值$y^{d}_{5}$, 比较$y^{d}_{5}$与$y_{\sum_{q}}$. 如果$y^{d}_{5}\geq y_{\sum_{q}}$, 向下执行; 否则$X^{d}_{1}= X^{d}_{5}$,转到Step $16$.
Step 15 当反射向量不能优于最差顶点的解, 并且在进行反向收缩得到的解仍然不能优于最差顶点的解, 说明搜索区域不好,应该跳出, 将所有的顶点执行一次收缩操作:$X_{u}=g(X_{\sum_{1}}+X_{u}),~~\forall u=\sum_{2},\cdots,\sum_{q}$. 转到Step $17$.
Step 16 令$X_{\sum_{q}}=X^{d}_{1}$,转到Step $2$.\
Step 17 结束. 2.4 粒子解码
定义供应优先级如下: 对于产品$i$在阶段$j$加工的批$k$, $suc(i,j,k)$表示产品$i$在阶段$j+1$ 供应优先级关系的 被约束批,$pre (i,j,k)$表示产品$i$在阶段$j-1$供应优先级关系的约束批, 后阶段被约束批开始加工时间必须在前阶段约 束批结束加工时间后. 定义库存优先级如下: $suc'(i,j, k)$表示产品$i$在阶段$j-1$存在库存优先级关系的被约束批, $pre'(i,j,k)$表示 产品$i$在阶段$j+1$ 存在库存优先级关系的约束批, 前阶段的被约束批结束加工时间必须在后阶段约束批开始加工时间后.
命题1 供应物料优先级$l=pre(i,j,k)$必须满足以下条件: \begin{eqnarray*} % \nonumber to remove numbering (before each equation) l=\min \{d|E_{i,j-1,dk}\geq 0,d\in N\},~~~\forall i\in P,j\in \end{eqnarray*} \begin{eqnarray*} R:j\geq 2,k\in N:b_{ijk}>0. \end{eqnarray*}
证明 论题中的条件有两层意思, 第一层为批$l$的$E_{i,j-1,lk}\geq 0$, 第二层为$l$是$d$中第一个满足$E_{i,j-1,dk}\geq 0$. 先证明第一层. $ E_{i,j-1,lk}$表示$b_{i,j-1,l}$结束,$b_{ijk}$开始时中间库存量. 该值等于$j-1$ 阶段从第$1$批到$l$为止总的产出量减去$j$阶段从第$1 $批到$k $为止总的消耗量. 显然,必须有$E_{ij-1,lk}\geq0$. 否则$j $阶段的$k $批将因缺少物料输入而不能加工. 第一层得证.
对于第二层,采用反证法求证.
假设$l\neq \min \{d|E_{i,j-1,dk}\geq 0\}$则有两种可能的情况: $ l< \min \{d|E_{i,j-1,dk}\geq 0\}$ 和$l> \min \{d|E_{i,j-1,dk}\geq 0\}$. 针对两种情况,分别讨论如下:
$1)$ $l< \min \{d|E_{i,j-1,dk} \geq 0\}$时,则有$E_{i,j-1,lk}<0$,不满足条件第一层,所以这种情况$l=pre(i,j,k)$ 不成立.
$2)$ $l>\min\{d|E_{i,j-1,dk}\geq0\}$时,满足$l-1\geq \min\{d|E_{i,j-1,dk}\geq0\}$. 因为中间 库存量$E_{i,j-1,l-1,k}\geq 0$,则$l-1$ 批在$k $批之前可以保证生产,$ l$不是必须在$k$批之前. 因此,这种情况$l=pre(i,j,k)$也不成立.
由以上两种可能情况的分析,表明$l=\min \{d|E_{i,j-1,dk}\geq 0\}$.
综上,完成命题$1$的证明.
命题2 库存约束优先级$l=pre'(i,j,k)$必须满足以下条件: \begin{eqnarray*} % \nonumber to remove numbering (before each equation) l=\min \{d|E_{ijdk}\leq E^{\max}_{ij},d\in N\},~~~\forall i\in \end{eqnarray*} \begin{eqnarray*} P,j\in R:j< r,k\in N:b_{ijk}>0\wedge \sum_{d\in \{0,1,\cdots,k\}}b_{ijd}> E^{\max}_{ij}. \end{eqnarray*}
证明 论题中的条件有两层意思, 第一层为批$l$的$E_{ij}^{\max}-E_{ijkl}\geq0$,第二层为$l$是$d$中第一个满足$E_{ij}^{\max}-E_{ijkd}\geq0$. 先证明第一层. 为保证$b_{ijk}$有足够的空间可以释放输出物, 显然第一层成立.
第二层采用反证法. 假设条件$l\neq \min\{d|E_{ij}^{\max}-E_{ijkd}\geq0\}$,则有两种可能情况: $l< \min\{d|E_{ij}^{\max}-E_{ijkd}\geq0\}$ 和$l >\min\{d|E_{ij}^{\max}-E_{ijkd}\geq0\}$. 分别对两种情况讨论:
$1)$ 当$l<\min\{d|E_{ij}^{\max}-E_{ijkd}\geq0\}$时, 则$E_{ij}^{\max}-E_{ijkl}\leq0$. $E_{ijkl}$将超过最大库存限制, 因此这种情况$l=pre'(i,j,k)$不成立.
$2)$ 当$l>\min\{d|E_{ij}^{\max}-E_{ijkd}\geq0\}$时, 后阶段的$l$前一个批$l-1$能够满足$l-1\geq \min\{d|E_{ij}^{\max}-E_{ijkd}\geq0\}$则 中间库存量$E_{ij}^{\max}-E_{ijk,l-1}\geq0$, 批$l-1$在批$k$结束之前开始能够保证满足最大库存限制约束, 而$l$不需要在批$k$结束之 前开始. 因此, 这种情况$l=pre'(i,j,k)$不成立.
由以上两种可能情况的分析,表明$l=\min\{d|E_{ij}^{max}-E_{ijkd}\geq0\}$.
综上,完成命题$2$的证明.
根据上述命题分析得出批之间的优先级关系,采用序列策略、时间策略和修复策略可以将粒子解码为问题的可行解. 序列策略可 以产生一个所有批节点的调度序列. 按照此序列调度,能够保证得到的解满足每批头尾节点、同任务批间、不同生产工序间形成的 供应物料和最大库存限制约束. 建立调度序列的过程如下:
Step 1 根据任务及分批结果, 确定所有头节点的数量$m=m_{1}+m_{2}+\cdots+m_{l}+\cdots+m_{e}$, $m_{l}$表示第$l$个任务的批数. 所有节点的数量为所有头节点数量的$2$倍. 头节点都放在前面, 尾节点都放在后面,对各节点依次编号.
Step 2 根据资源约束项目网络图,建立优先级集合$P$.
Step 3 调度序列是将节点安排在序列 的位置上. 选择第一个位置$h=1$.
Step 4 建立已完成调度节点的集合$E$,令$E=\emptyset$.
Step 5 建立每个节点的紧前节点集合, 用$A_{j}$表示第$j$个节点的紧前节点集合.
Step 6 建立紧前集合为空的集合$B=\{j|A_{j}=\emptyset\}$, 表示对节点$j$有约束的节点都已经调度完.
Step 7 由于批的头节点和尾节点是分开调度的. 实际上批的头尾节点在相同设备上是紧邻调度的, 因此同一批的头节点安排完后,在同设备的其它批头节点不能开始加工. 在此,将其它头节点放到集合$C$,称为屏蔽集合.
Step 8 建立可以调度的节点集合$Y=B-C-E$, 在本次安排中可以选择.
Step 9 选择节点$k\in Y$,安排给$h$位置.
Step 10 判断$h$是否等于$2m$,如果等于向下执行; 如果不等于,令$h=h+1$,更新已调度完节点集合$E$. 转到Step $5$.
Step 11 结束.
时间策略是按照调度序列来安排批节点时间,产生批节点时间的步骤如下:
Step 1 设循环索引$i\in\{1,2,\cdots,2m\}$,令$i=1$. 用$s_{j}$表示阶段$j (j=1,2,\cdots,r)$上新节点可以安排的时间, $o_{i}$表示节点$i$对应批的加工时间. 因为一台设备每次只加工一个批, $s_{j}$是随着设备上安排的节点累积增加的,令$s_{j}=0$.
Step 2 $h=\sum_{i}$,$t_{h}$表示节点$h$的调度时间. 判断$h$为头节点还是尾节点. 如果是头节点,向下执行; 如果是尾节点, 转到Step $4$.
Step 3 找到其供料的紧前节点$k$,$t_{h}\geq t_{k} $. 找到节点$h$加工的设备$j$,$h$可以安排在设备上的最早时间$s_{j}$, $t_{h}\geq s_{j}$. 令$t_{h}=\max(t_{k},s_{j})$, 更新$s_{j}=t_{h}+o_{h}$. 转到Step $5$.
Step 4 找到其最大库存的紧前节点$k$,$t_{h}\geq t_{k} $. 计算调度对应的头节点编号$g=h-m$. $t_{h}\geq t_{g}+o_{g}$, $t_{h}=\max(t_{k},(t_{g}+o_{g}))$ ,找到节点$g$加工的设备$j$, 更新$s_{j}=t_{h}$.
Step 5 判断$i$是否等于$2m$. 如果不等于令$i=i+1$,转到Step $2$; 如果等于向下执行.
Step 6 结束.
通过上述步骤得到的批节点时间还需采用修复策略给予修正, 以使同一批头尾节点的时间差等于批加工时间. 所采用的修复策略是: 找到不满足要求的节点,移动该节点到符合要求的时刻; 根据时间策略重新安排在调度序列中该节点后面的节点. 2.5 算法实现过程
依据上述编码和解码原则, 将单纯形搜索和粒子群算法相结合的完整算法实现步骤如下:
Step 1 初始化参数,设置迭代次数、种群规模, 粒子的维数、位置和速度的范围.
Step 2 随机产生初始种群.
Step 3 利用分批和调度方法对粒子信息解码,得出调度方案, 计算目标函数值,记录个体最好解和全局最好解.
Step 4 用种群粒子当前位置生成单纯形搜索的顶点.
Step 5 执行单纯形搜索. 单纯形搜索产生的新解替换最坏的顶点,或进行所有顶点位置的收缩.
Step 6 将新的顶点信息赋给种群粒子当前位置.
Step 7 更新种群个体和全局信息.
Step 8 判断是否满足终止条件,如果满足向下执行, 如果没有满足则用粒子群迭代公式更新粒子的位置和速度,执行Step $3\sim8$.
Step 9 结束. 3 实例验证及分析
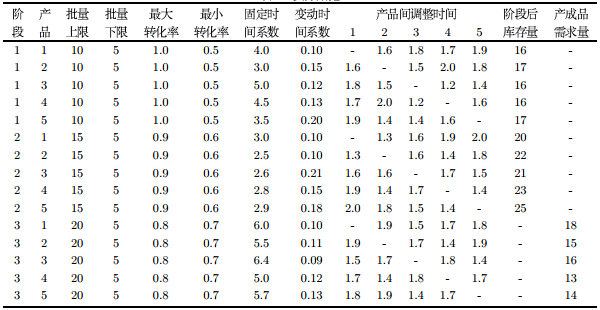
某石化企业拥有两条年产万吨和一条年产$1500$吨的多品种生产线. 以其中一条年产万吨聚酯产品的生产线为例,该生产 线包括第一脂化反应、第二脂化反应、缩聚反应这三个生产阶段. 生产线上每个反应釜的釜量有上下限要求: 上限是反应釜的 最大容量, 下限则由反应条件和技术要求决定. 因反应釜一直处于高温的状态下, 反应釜内的液体量若太少,会造成反应釜的空 烧, 对反应釜设备本身和成品的质量都有损害. 由于该生产线脂化反应釜与缩聚反应釜的容量不同,使其单次生产批量也不 等. 此外,当不同种产品进行切换生产时, 三个生产阶段的反应釜都需要清洗. 清洗过程会造成生产时间损失, 清洗所需用料又 会产生过度料的消耗费用, 因此该企业规定每周的产品切换不超过$5$种. 目前该企业是以每周为一个时间段来做调度 时间表, 有关实际数据见表 1. 表 2是基于实际数据的软件计算结果, 测试时最大时间限制在$3600$ 秒.
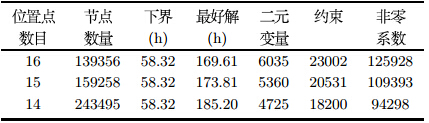
从表 2的计算结果可以看出,随着位置点数量不同,问题的求解规模在发生变化. 位置点的数量增加$15 \%$时,二元变量、约束条件、非零系 数的数量增加$30\%$以上,搜索的节点数量降低了$40\%$以上,这说明软件求解分批与调度混合整数规划模型的能力受到位置点和批次数量的 影响较大. 位置数量为$16$时软件得到最好解. 该位置数量介于最小值和最大值之间,原因在于位置数量若等于最少批次,批量的取值则为最 大批量或接近最大批量,这样就会导致缩小可行区域而影响解的质量,若位置数量等于最大批次,则因计算规模增加又会影响搜索解的速 度和质量. 图 1给出的是基于最好解的分批和调度甘特图.
 |
| 图 1 基于最好解的分批和调度甘特图 |
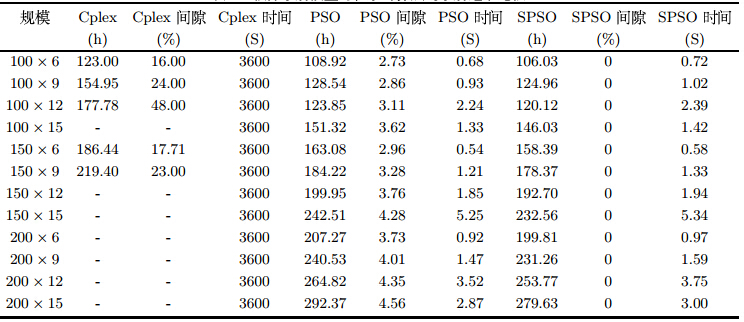
SPSO算法求解性能可从求解能力、求解质量和求解时间三个方面衡量: 求解能力是算法求解大规模复杂问题的能力; 求解质量 是算法求解值$S$接近最佳值(理想值)$ S^{*}$的程度, 可用偏差$gap=(S-S^{*})/ S^{*}$作为度量标准; 求解时间是算法求解所 花费时间的长短. 本文提出的SPSO算法与求解软件Cplex、 标准 PSO算法的计算结果的比较见表 3. 表 3中,问题规模是需求总 量和任务数的组合,任务数为阶段数与产品数的乘积,阶段数取$3$, 产品数取$2\sim5$,SPSO算法与PSO 算法参数取值相同,种 群规模取$500$,算法最大迭代次数为$10000$代. 从表 3可以看出: 软件求解的能力随着产成品需求量的增加而下降, 当需求量增至$200$吨时软 件求解在$3600$秒内都未能得到可行解, 其原因在于随着需求量和任务数量的增加, 约束条件和非零系数增加,模型求解难度加大. 可见,软件求 解只适合小规模问题求解,大规模问题求解时采用粒子群算法更加有效. 此外,求解结果表明,SPSO与PSO两种算法计算时 间相近, 但SPSO求解质量优于PSO.
适应市场需求多样化和个性化的发展趋势, 流程工业企业已由单一品种大批量生产转向多品种成批轮番生产, 与此同时,在其生产计划与调度上面 临着诸多比以往更加复杂而又亟待解决的新问题. 本文针对共享流程资源设备的多品种成批轮番生产的分批与调度集成问题, 构建的基于连续时间 和批次之间优先级关系的分批和调度集成决策模型, 以及给出的模型求解的二维编码改进粒子群算法, 拓展了流程式多品种成批轮番生产分批与 调度集成理论、决策模型及其智能算法, 而且实际背景算例验证所构建的模型和给出的改进粒子群算法, 克服了目前已有算法只适用于小规模 或模拟生产需要而解决不了大规模实际生产调度问题的缺陷, 从而为面向流程生产实际的大规模多品种成批轮番生产的分批和调度集成决策提 供了具有应用价值的智能优化算法和工具, 也为相关软件开发及生产实时调度与控制提供了应用参考.
| [1] | Garey M R, Johnson D S. Computers and intractability: A guide to the theory of NP-completeness[M]. San Francisco: Freeman, 1979. |
| [2] | Potts C N, Baker K R. Flow shop scheduling with lot streaming[J]. Operations Research Letters, 1989, 8(6): 297-303. |
| [3] | Chen J, Steiner G. Lot streaming with detached setups in three-machine flow shops[J]. European Journal of Operational Research, 1996, 96(3): 591-611. |
| [4] | Ghafari E, Sahraeian R. A two-stage hybrid flowshop scheduling problem with serial batching[J]. International Journal of Industrial Engineering and Production Research, 2014, 25(1): 55-63. |
| [5] | Shabtay D. The single machine serial batch scheduling problem with rejection to minimize total completion time and total rejection cost[J]. European Journal of Operational Research, 2014, 233(1): 64-74. |
| [6] | Trietsch D, Baker K R. Basic techniques for lot streaming[J]. Operations Research, 1993, 41(6): 1065-1076. |
| [7] | Liu S C. A heuristic method for discrete lot-streaming with variable sublots in a flow-shop[J]. International Journal of Advanced Manufacturing Technology, 2003, 22(9-10): 662-668. |
| [8] | Liu L L, Ng C T, Cheng T C E. Scheduling jobs with release dates on parallel batch processing machines to minimize the makespan[J]. Optimization Letters, 2014, 8(1): 307-318. |
| [9] | Bose S K, Bhattacharya S. A state task network model for scheduling operations in cascaded continuous processing units[J]. Computers and Chemical Engineering, 2009, 33(1): 287-295. |
| [10] | Shi B, Yan L, Wu W. Rule-based scheduling of single-stage multiproduct batch plants with parallel units[J]. Industrial and Engineering Chemistry Research, 2012, 51(25): 8535-8549. |
| [11] | Allahverdi A, Ng C T, Cheng T C E, et al. A survey of scheduling problems with setup times or costs[J]. European Journal of Operational Research, 2008, 187(3): 985-1032. |
| [12] | Behnamian J, Ghomi S M T, Jolai F, et al. Realistic two-stage flowshop batch scheduling problems with transportation capacity and times[J]. Applied Mathematical Modelling, 2012, 36(2): 723-735. |
| [13] | 霍满臣, 唐立新. 基于到达时间两台并行机上在线批调度[J]. 控制与决策, 2009, 24(12): 1826-1830.Huo Manchen, Tang Lixin. On-line batch scheduling with real time on two parallel machines[J]. Control and Decision, 2009, 24(12): 1826-1830. |
| [14] | Mathirajan M, Bhargav V, Ramachandran V. Minimizing total weighted tardiness on a batch-processing machine with non-agreeable release times and due dates[J]. International Journal of Advanced Manufacturing Technology, 2010, 48(9-12): 1133-1148. |
| [15] | 宫华, 唐立新. 并行机生产具有等待时间限制的成批运输协调调度问题[J]. 控制与决策, 2011, 26(6): 921-924.Gong Hua, Tang Lixin. Scheduling production on parallel machines and batch delivery with limited waiting time constraint[J]. Control and Decision, 2011, 26(6): 921-924. |
| [16] | Yang X, Xu Q, Li K. Flare minimization strategy for ethylene plants[J]. Chemical Engineering and Technology, 2010, 33(7): 1059-1065. |
| [17] | Wang I L, Yang T, Chang Y B. Scheduling two-stage hybrid flow shops with parallel batch, release time, and machine eligibility constraints[J]. Journal of Intelligent Manufacturing, 2012, 23(6): 2271-2280. |