2. 过程优化与智能决策教育部重点实验室, 合肥 230009
2. MOE Key Laboratory of Process Optimization and Intelligent Decision-Making, Hefei 230009, China
0 引言
Supply Hub也称为Vendor Hub,VMI (vendor managed inventory) Hub等[1].国内称作集配中心,它一般位于制造商附近,用于存储所有或部分供应原材料,根据协议,只有当原材料被消 耗时才支付相应的费用[2]. Supply hub处于供应商与制造商之间的流通环节,是一种适应制造商JIT生产的供应链管理战略手段,它将制造商的客户化活动延迟 至接到顾客需求订单,实现制造商原材料供应与JIT生产的无缝连接.实践中,由于市场的不确定性导致生产计划不连贯以 及供应链信息共享不充分引起的信息交互断层,导致从Supply Hub到制造商车间的原材料配送出现订单到达随机性强、配送计划变化快等特点,严重影响JIT生产原材料配送准时性, 甚至造成生产线缺货停工待料,这使得Supply Hub协同运作模式在降低供应链成本、提高供应链绩效等方面的效应没有得到很好的体现.
关于Supply Hub ``集"、``配"问题的研究,也引起了国内外许多学者的关注. Erenguc[3]对JIT生产的配送问题进行了研究,其研究指出JIT生产方式需要供应商通过小批量多批次的补货方式来保证. Kreng等\,[4]研究了制造商与装配车间的配送问题,提出了定时定量配送和经济批量配送的配送策略. Kim等[6] 研究了单供应商、单零售商供应链的JIT 配送协同问题,提出了lot-splitting(批量分割)的订单分解方式,降低供应链的配送成本. Kreng[4]研究了生产间隔与配送间隔相等条件下,单一产品和多种产品的多级供应链生产与配送调度问题. Kim等[5]研究了需求确定条件下供应商的生产和配送间隔优化问题,研究表明生产间隔为配送间隔的整数倍时,系统的平均总成本最小. Low等[6]在生产与配送协同的研究中将时间窗的概念引入模型,并设计了求解该模型的改进遗传算法.马士华等[7]以Supply Hub 运作模式为背景,研究同步物流下装配系统中各节点的生产与配送调度问题,建立了供应链各参与方的生产与配送模型. 马士华等[8]研究了一种基于Supply Hub运作模式,在供应商之间可以共享补货及库存信息的条件下,供应商协同补货策略.
以上文献多研究供应商到制造商间的``集"物流,研究供应商生产与配送的协同问题,未考虑订单的随机性对JIT生产的影响.本文以Supply Hub出库调度为研究对象,将延迟理论引入配送调度,建立基于Milk-run的延迟滚动调度模型,为解决Supply Hub 订单随机性强,准时性要求高问题提供了一种可借鉴的模型和算法,进一步丰富供应链生产和配送协同决策的理论研究,并为Supply Hub模式的JIT配送提供决策参考. 1 问题描述和参数定义 1.1 问题描述
某制造商采用基于Supply Hub的协同运作模式实施JIT生产和采购活动.生产计划滚动发布,各供应商结合生产计划和库存信息,为Supply Hub补货. Supply Hub 根据车间看板信息对各种原材料匹配成套,直送到各车间的生产线边,其活动关系如图 1所示.
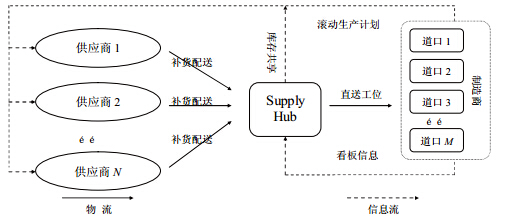 |
| 图 1 基于supply-hub的物流协同 |
设制造商共有$M$个车间,各车间根据生产线的生产进度向Supply Hub 发送原材料需求看板信息,Supply Hub根据看板信息,完成原材料的匹配、分拣,每隔时间$T$ 对分拣好的原材料调度一次,再由配送车辆直送到各车间生产线边.要求从Supply Hub接到看板信息到物料送达生产线边,时间必须控制在配送时间窗以内,否则,将引起生产线的停产,求配送成本最小的配送方案.
本文的研究做以下假设:
假设1 每批原材料的匹配、拣选具有固定的调整准备时间,因此调度模型中可以不考虑每批原材料的匹配、拣选时间;
假设2 Supply Hub一般位于制造商附近,忽略模型中的路径选择问题,车辆配送的时间成本只与一次配送道口的个数有关,而与距离无关.
假设3 从Supply Hub到车间采取Milk-run方式(循环取货)配送,调度间隔固定,调度批量为调度间隔内制造商对各种原材料的需求总量. 1.2 参数定义
$M$:制造商车间道口总数;
$k$:配送车辆序号;
${Q}_{k}$:车辆车载体积;
${v}_{i}$:订单物料箱的体积;
${c}_{0}$:配送车辆固定成本参数;
${c}_{1}$:配送车辆可变成本参数;
${c}_{2}$:时间成本参数;
${c}_{3}$:延迟成本参数;
${HT}_{i}$:订单{i}的要求到货时间(时间窗上限);
${AT}_{i}$:订单{i}到达Supply Hub的时间(时间窗下限);
${T}$:调度时间间隔,$2{T}\le{HT}_{i}-{AT}_{i}$;
${n}$:调度次序号,$n=1,2,\cdots$;
${y}_{ij}$:第{i}个订单为第{j}道口的订单;
${x}_{ik}$:第{k}辆车装载第{i}个订单. 2 基于延迟的出库调度模型
由于JIT生产对时间性和灵活性的高度要求,从Supply Hub到车间的``最后一公里"配送首先关心的是能否及时到货,其次才是节约的成本.各制造车间的看板信息以流的形式发送到Supply Hub,从Supply Hub到车间的配送采取Milk-run方式,调度周期为$T$,配送成本分为车辆成本、时间成本和延迟成本三部分.
1)车辆成本.车辆成本分为固定成本和变动成本.固定成本,即:由于Supply Hub的配送车辆循环利用,多使用一辆车就必须为这 辆车花费成本,包括车辆维护费用,车辆资产折旧,驾驶员工资等.设${p}$为本次调度使用的车辆数,则固定成本记为: \begin{equation} {c}_{0} * {p}\qquad \end{equation} \begin{equation} {p} = \sum_{k} \ {b}_{k} \end{equation} \begin{equation} {b}_{k} = \left\{ \begin{array}{ll} 1,& \sum_{i}\ \ textit{x}_{ik}>0\\ 0,& \sum_{i}\ \ textit{x}_{ik}=0\\ \end{array} \right. \end{equation}
变动成本是指与车辆满载相关的成本,车辆满载量越大,车辆的利用效率越高,配送成本越低;反之,如果车辆满载率越低, 成本也就越大.可变成本记为: \begin{equation} \bigg( 2{Q}_{k} - \sum_{i}{v}_{i}{x}_{ik}/{Q}_{k} \bigg){c}_{1}*{p} \end{equation}
因此,总车辆成本=固定成本+变动成本,其公式表示如下: \begin{equation} f(x_{ik}) = \sum_{k}\bigg[\bigg(2{Q}_{k} - \sum_{i}{v}_{i}{x}_{ik}/{Q}_{k} \bigg){c}_{1} + {c}_{0} \bigg]*{b}_{k} \end{equation}
2)时间成本.由于配送采用Milk-run模式,车辆是循环利用的,如果一次配送中车辆只配送一个道口,则车辆排队卸货的时间较短, 车辆重复利用率也就高.因此,调度方案中一辆车服务的道口越多,其成本就越大.时间成本表示如下: \begin{equation} \ {g}({x}_{ik}) = \sum_{k}\bigg[\sum_{j}\bigg(\sum_{i}\bigg){x}_{ik}{y}_{ij}\bigg]*{c}_{2} \end{equation}
3)延迟成本.由于配送采用Milk-run模式,调度采用滚动方式,每次调度时, Supply Hub 中的订单可以本次调度出库配送,也可以遗留下来等到下次调度出库,而遗留的订单产生延迟成本.延迟成本表示如下: \begin{equation} \ {h}({x}_{ik}) = \sum_{i}({n}*{T}-{A}{T}_{i})\bigg(1-\sum_{k}{x}_{ik}\bigg)*{c}_{3} \end{equation} 其中${n}*{T}$表示第${n}$次调度订单的出库时间.
以总配送成本最低为目标函数,建立基于延迟的出库调度模型:

约束条件中,式(8)每个订单不能超过其最大时间窗;式(9)车辆不能超载;式(10)车辆只能一对一配送;式(11)看板不能分拆,即:一个看板 所需原材料只能有一辆车配送.
以上模型为一个MKP (multidimensional 0-1 knapsack problem)模型,即:多维0/1背包问题模型.传统0-1背包问题仅考虑物品的一种约束,如装入背包的物品的总重量不能超过 背包的重量限制,而多维0/1背包问题需要同时满足两个或两个以上的约束. 3 调度模型算法
目前求解MKP问题的算法主要有两大类:精确算法和启发式算法.精确算法{[9, 10, 11, 12] }如隐枚举法、分枝定界法等;启发式算法{[13, 14, 15, 16]}主要包括:遗传算法、蚁群算法、免疫算法、禁忌搜索算法等,此类 算法具有框架灵活、与具体问题本身无关等优点,应用广泛.本文基于免疫学说,将目标函数和约束条件当做抗原,将抗体当 做问题的解集,模拟生物免疫系统的克隆和选择,求解目标的近似最优解. 3.1 算法流程
多目标优化模型在求解过程中要么求解时间过长要么很难得到最优解,本文设计了求解多目标滚动模型的免疫算法,其流程如图 2所示.
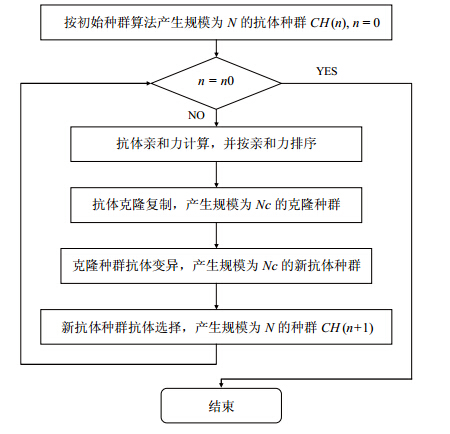 |
| 图 2 免疫克隆算法流程 |
首先要对MKP的解进行编码.对于{m}个车辆{n}个看板,其解空间为${m}*{n}$的矩阵.在这个矩阵中,当${x}_{ik} = 1$ 时,表示看板{i} 中需要的原材料放入车辆{k};当${x}_{ik} = 0$时,表示看板{i}中需要的原材料不放入车辆{k}.对于 这个基因就只存在这两种情况,使用长度为${m}* {n}$位的二进制字符串构成的矩阵表示一个抗体. 3.3 初始抗体群
首先,按道口分配车辆生成初始抗体,即:一辆车只装一个道口的订单;其次,初始抗体克隆复制生成初始抗体种群.免疫克 隆算法相比遗传算法没有个体交配环节,不存在近亲繁殖问题.设初始种群规模$N$,初始种群为$Ch(n)$, $n=0$,$n$为迭代次数,$n0$为最大迭代次数. 3.4 亲和力和相似度
亲和力是指抗体与抗原的相似程度,亲和力越高,抗体克隆的数量越多.本文的模型有三个子目标,三个子目标都是越少越好,即: $z = f(x_{ik})+g(x_{ik})+{h(x_{ik})}$. 3.5 克隆选择
定义克隆规模函数: \[{N}_{c} = \sum_{i} \lceil \beta*{N}/{No} \rceil(12)\] ${N}_{c}$ 是克隆后抗体种群的规模; $\beta$是克隆系数,用来控制抗体种群的规模; {No}是抗体在抗体种群的按亲和力由大到小的排序序号, ``$\lceil$\ $\rceil$" 表示向上取整.种群中第{No}个抗体克隆复制自身的数量是$\lceil \beta*{N}/{No} \rceil $.克隆复制后的种群按抗体亲和力大小进行赌轮盘选择,亲和力越大的抗体克隆复制自身的概率越大. 3.6 变异算子
变异是指生物体子代与亲代的遗传基因发生改变的现象.克隆选择保证了抗体的优秀基因得到继承,而免疫克隆算法高概率的变异 实现了抗体的多样性,本文采取基本位变异算子,即:随机选取抗体中的某位基因,发生突变. 4 算例分析 4.1 算例数据
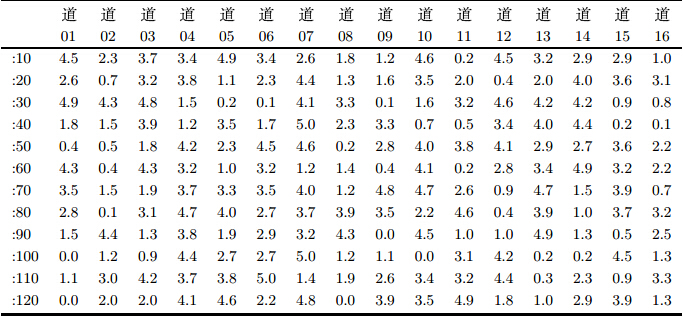
某集配中心为4个车间共16个道口配送原材料,设每辆车的车载为5单位,配送时间窗要求为集配中心接到订单后60单位时间 内将物料送达车间(道口).一般情况下,2${T} \le {HT}_{i}-{AT}_{i}$,否则,模型将退化为不带延迟的调度模型,本文选取的调度周期为10单位时间.另外,为方便 分析,假设同一个调度周期中的订单为调度周期的起始时间,随机提取一段时间内的看板数据,其详细数据如表 1所示.
1)最优结果,取$c_{0}$、$c_{1}$、$c_{2}$、$c_{3}$的参数都为1,通过本文设计的模型和算法求得计算结果如表 2所示.
2)各参数灵敏度分析
 代表调度模型的车辆成本因子.图 3中成本$c_{0}$、成本$c_{1}$为直线关系,图 4中$c_{0}$、$c_{1}$与满载率
成向上的凸线.意味着随$c_{0}$、$c_{1}$的增加,满载率越来越大,遗留的看板也就越多,最后趋于与$x$轴平行的直线,满载率最大.
代表调度模型的车辆成本因子.图 3中成本$c_{0}$、成本$c_{1}$为直线关系,图 4中$c_{0}$、$c_{1}$与满载率
成向上的凸线.意味着随$c_{0}$、$c_{1}$的增加,满载率越来越大,遗留的看板也就越多,最后趋于与$x$轴平行的直线,满载率最大.
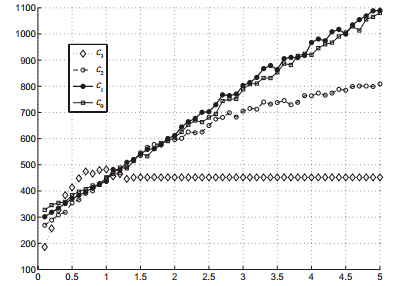 |
| 图 3 参数与成本的灵敏度分析 |
 代表调度模型的时间成本因子.图 3中成本$c_{2}$曲线随着$c_{2}$的增加向下偏移,图 4中$c_{2}$满载率呈向上凸曲线,
与$c_{0}$、$c_{1}$与满载率的曲线形状基本相同,也就是说随$c_{3}$的增加调度方案偏好于遗留订单等待下次调度,优先将满载
的订单调度出库.
代表调度模型的时间成本因子.图 3中成本$c_{2}$曲线随着$c_{2}$的增加向下偏移,图 4中$c_{2}$满载率呈向上凸曲线,
与$c_{0}$、$c_{1}$与满载率的曲线形状基本相同,也就是说随$c_{3}$的增加调度方案偏好于遗留订单等待下次调度,优先将满载
的订单调度出库.
 代表车辆调度模型的时间因子.成本$c_{3}$曲线随$c_{3}$的增加,先增加,后减少,最后与$x$轴平行,图 4中$c_{3}$满载率曲
线表明:随$c_{3}$ 的增加满载率逐渐减少,直至与$x$
轴平行.意味着随$c_{3}$的增加,调度方案偏好于调度方案,遗留的方案反而减少,最后随着$c_{3}$的增加,调度方案偏好于
全部将订单调度,变为全部调度的先到先服务调度策略.
代表车辆调度模型的时间因子.成本$c_{3}$曲线随$c_{3}$的增加,先增加,后减少,最后与$x$轴平行,图 4中$c_{3}$满载率曲
线表明:随$c_{3}$ 的增加满载率逐渐减少,直至与$x$
轴平行.意味着随$c_{3}$的增加,调度方案偏好于调度方案,遗留的方案反而减少,最后随着$c_{3}$的增加,调度方案偏好于
全部将订单调度,变为全部调度的先到先服务调度策略.
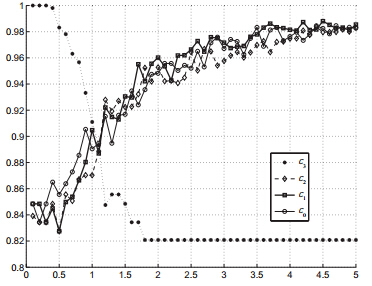 |
| 图 4 参数与满载率的灵敏度分析 |
先到先服务:即看板所需原材料出库调度时不延迟,当前批次的到达的看板全部调度;最大延迟:即不考虑车辆成本和时间成本,只考 虑时间成本,等时间成本最小时再调度的策略.延迟调度:即本模型的调度策略.通过表 3的对比结果,我们可以看到延迟调度的满 载率到达了93.25\%,明显高于最大延迟的85.72\%和先到先服务的78.58\%.一方面是由于通过延迟因子,将部分调度成本较 高的订单遗留下来,提高了车辆的满载率;另一方面,延迟又将能够调度的看板尽早出库,避免了看板扎堆调度、车辆运力不足 以及车辆排队装卸等问题.
本文在分析Supply Hub 出库调度的特点的基础上,将延迟理论引入出库调度,考虑Supply Hub 准时制配送的车辆成本、时间成本和延迟成本的基础上,建立Supply Hub 准时配送的滚动调度模型,它与传统调度模型的不同在于: 1)基于Supply Hub与制造商很近的实际情况,忽略车辆的路径问题,而着重优化订单的分配问题; 2)订单连续到达,且订单到达时间具有随机性,因此,调度模型具有滚动性,而非常规的一次调度模型; 3)因为调度模型具有滚动性的特点,因而,订单要具有取舍性,要么调度出库,要么留下下次调度,与常规调 度和订单全部调度有所不同.另外,由于本文多目标优化模型在求解过程中要么求解时间过长要么很难得到最优解,所以本 文设计求解该多目标滚动模型的免疫算法,使得求解时间和解的质量都得到很大程度的改变.从模型算例分析的决策结果可以看出, 模型能有效降低订单随机到达、配送准时性要求高的Supply Hub准时制配送的配送成本.
| [1] | Huang Q X, George Q. Supply hub in industrial park (SHIP): The value of freight consolidation[J]. Computers & Industrial Engineering, 2013, 65(1): 16-27. |
| [2] | Huang K, Ma S H. Coordinated Replenishment with information sharing between two suppliers based on supply-hub[C]// International Conference on Management Science and Engineering-Annual Conference Proceedings, Australia: IEEE, 2010: 403-409. |
| [3] | Agarwal A, Colak S, Erenguc S. A Neurogenetic approach for the resource-constrained project scheduling problem[J]. Computers & Operations Research, 2011, 38(1): 44-50. |
| [4] | Kreng B, Wang I C. Economical delivery strategies of products in a JIT system under a global supply chain[J]. International Journal of Advanced Manufacturing Technology, 2005, 26(1): 1421-1428. |
| [5] | Kim S L, Ha D. A JIT lot-splitting model for supply chain management enhancing buyer-supplierlinkage[J]. International Journal of Production Economics, 2003, 86(1): 1-10. |
| [6] | Low C, Li R K, Chang C M. Integrated scheduling of production and delivery with time windows[J]. International Journal of Production Research Forthcoming, 2013, 51(3): 897-909. |
| [7] | 马士华, 王青青. 同步物流系统下准时化生产与配送调度问题研究[J]. 中国管理科学, 2012, 20(6): 126-131.Ma Shihua, Wang Qingqing. Research on production and distribution scheduling in assembly system with synchronous logistics[J]. Chinese Journal of Management Science, 2012, 20(6): 126-131. |
| [8] | 马士华, 黄 妮, 何媛媛. 基于Supply Hub运作模式的供应商协同补货策略研究[J]. 管理工程学报, 2011, 25(1): 26-33.Ma Shihua, Huang Ni, He Yuanyuan. A coordinated replenishment policy between two suppliers based on the model of using supply-hub[J]. Journal of Industrial Engineering and Engineering Management, 2011, 25(1): 26-33. |
| [9] | 王军, 李端. 多项式0-1规划中隐枚举算法的改进及应用[J]. 系统工程理论与实践, 2007, 27(3): 21-27.Wang Jun, Li Rui. A new implicit enumeration method for polynomial 0-1 programming and applications[J]. Systems Engineering——Theory & Practice, 2007, 27(3): 21-27. |
| [10] | 白凤, 朱金福, 高强. 基于列生成法的不正常航班调度[J]. 系统工程理论与实践, 2010, 30(11): 2036-2045.Bai Feng, Zhu Jinfu, Gao Qiang. Disrupted airline schedules dispatching based on column generation methods[J]. Systems Engineering——Theory & Practice, 2010, 30(11): 2036-2045. |
| [11] | Watters L J. Reduction of integer polynomial problems to zero-one linear programming problems[J]. Operations Research, 1981, 15(6): 1171-1174. |
| [12] | Layeb A. A hybrid quantum inspired harmony search algorithm for 0-1 optimization problems[J]. Journal of Computational and Applied Mathematics, 2013, 253(1): 14-25. |
| [13] | Liu F H, Shen S Y. The fleet size and mix vehicle routing problem with time windows[J]. Journal of the Operational Research Society, 1999, 50: 721-732. |
| [14] | Pundoor G, Chen Z L. Joint cyclic production and delivery scheduling in a two-stage supply chain[J]. International Journal of Production Economics, 2009, 119(1): 55-74. |
| [15] | Xu J, Nelson B L, Hong L. An adaptive hyper-box algorithm for high-dimensional discrete optimization via simulation problems[J]. Informs Journal on Computing, 2013, 25(1): 133-146. |
| [16] | Sedghi M, Aliakbar-Golkar M, Haghifam M. Distribution network expansion considering distributed generation and storage units using modified PSO algorithm[J]. International Journal of Electrical Power & Energy Systems, 2013, 5(2): 221-230." |