0 引言
为了抑制住房价格快速上涨、增加住房供给, 政府采取了增加土地供给、提高企业融资限制等多项调控政策, 督促房地产开发企业加快住房开发与销售. 然而, 住房供给的形成过程包含了开发企业多个复杂决策环节. 政府的调控政策能否有效增加市场供给?开发企业如何做出土地购买、住房开发与销售决策, 又受到哪些因素影响?为了回答这些问题, 需要针对房地产开发企业供给决策行为进行深入研究.
目前,关于开发企业供给行为的学术研究, 主要以单一项目或决策环节为分析对象, 以项目或决策环节的利润最大化为目标. 如: 在土地储备决策研究中, 刘洪玉等[1]以土地储备收益最大化为目标构建理论模型, 指出开发企业的土地储备规模主要受到持有成本和预期收益两项因素影响. 在住房开发决策研究中,Titman[2], Somerville[3]和Quigg[4]以单一地块为研究对象, 应用实物期权理论分析了地块"等待的价值",指出由于存在市场风险, 开发企业往往会推迟项目的开发时间以获得更高的投资回报; Sirmans等[5],Suen等[6], Ott等,[7]研究了大宗土地项目中企业的分期开发行为. 在住房销售决策研究中,Ooi等[8], Ott等[7]针对大宗项目的销售环节, 分析了开发企业分期销售的动机与影响因素; 此外, Lai等[9]研究了开发企业的最优预售时点选择以及最优合同策略, Chan等[10], Chan等[11]运用博弈论方法研究了最优预售策略及其影响因素.
虽然上述研究已经对开发企业的主要决策环节进行了详细分析, 但我们常常可以观测到开发企业的实际供给行为与这些研究提出的最优策略不完全一致. 比如, 开发企业出于巩固市场地位、垄断区域市场、维持企业开发活动的连续性等目的, 可能以超常价格竞地或者过量储备土地; 再如, 一些刚刚进入市场的新兴企业,为了尽早占领市场、扩张势力, 可能将仍然具备储备潜力的地块提早开发并销售以回笼资金.
以往研究对上述现象的解释能力不足, 其中一个重要原因就在于这些理论模型是以单一项目或决策环节为研究对象的, 没有充分考虑各个决策环节之间的相互影响. 为了弥补以往学术研究的不足,提高理论模型对开发企业行为的解释能力, 本文提出了综合考虑房地产开发企业主要决策环节的理论分析模型, 通过理论模型与实证检验对开发企业的供给决策行为进行分析. 需要指出的一点是, 本文涉及的决策环节仅包含开发企业正常经营过程中的主要决策环节, 而不包含进入和退出市场的决策. 1 开发企业主要决策环节描述与模型建立
总结开发企业经营目标与经营活动中的主要决策环节如图 1所示. 开发企业具有保持企业持续经营以及追求企业长期总经营利润最大化的目标要求, 在经营活动中主要通过土地购买、住房开发、住房销售以及融资活动对土地储备量、可售住房持有量、现金持有量 以及融资总额四部分资产进行管理.
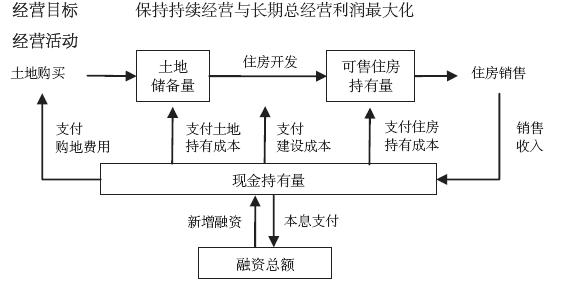 |
| 图 1 开发企业经营目标与经营活动中的主要决策环节 |
假设开发企业的决策可以离散化到每一个决策期$t$(半年或一年), 在任一决策期$t$ (=1,2,$\cdots$)内, 开发企业都要做出土地购买量$B_t$、住房开发量$D_t$、住房销售量$S_t$与融资数量$U_t$的经营决策, 使得第$t$期末的现金持有量、土地储备量、可售住房持有量与融资总额分别达到$K_t$, $L_t$,$H_t$,$SK_t$.
在土地管理方面,土地购买与住房开发活动决定了企业土地储备的规模, 其动态关系为$L_t=L_{t-1}+B_t-D_t$. 考虑到住房开工前需要完成规划设计及其他审批, 假设当期购地不能用于当期开发建设, 即第$t$期可以进行开发的土地规模上限为期初土地储备量,$D_t\leq L_{t-1}$.
在住房管理方面,住房开发与销售活动决定了可售住房的持有数量, 假设土地平均容积率为$\eta$, 可售住房持有量的动态关系为$H_t=H_{t-1}+D_t\eta-S_t$. 由于存在建设周期,假设当期开发的住房不能在当期销售, 需要经历一期的时间达到可售要求, 即第$t$期住房销售量的上限为期初可售住房持有量,$S_t\leq H_{t-1}$.
在融资管理方面, 认为所有外部资金来源为开发企业提供了一个备用的现金池, 融资额度上限不与单一地块或项目挂钩,而与开发企业的总资产挂钩, 即需要满足$SK_t\leq\beta$$V_{t-1}$. 其中,$\beta$为融资限制程度, 越低表示融资限制越严格, $V_{t-1}=K_{t-1}+L_{t-1}P_{L(t-1)}+H_{t-1}P_{H(t-1)}$代表开发企业第$t-1$期末的总资产. $P_{Ht}=\theta_t(1+\lambda)P_{H0}$为住房价格, 价格因子$\theta_t$服从几何布朗运动, 满足d$\theta_t/\theta_t=\alpha_\theta$d$t+\beta_\theta$d$z$, $\alpha_\theta$表示价格增长的长期趋势,$\beta_\theta$表示价格风险, $P_{H0}$为价格初值,$\lambda$表示开发企业的定价势力; $P_{Lt}=\eta(\theta_tP_{H0}-(1+\mu_C)^tC_{C0})(1+\delta)$为土地价格, $\mu_C$表示平均建设成本增长率,$C_{C0}$为平均建设成本初值, 此外由于土地市场和住房市场的供求关系相对独立, 引入土地价格风险系数为$\delta$,假设$\delta$是一个均值为0, 标准差为$\delta_0$的正态分布. 第$t$期开发企业需要支付总本息$rSK_{t-1}$, 其中$\underline{r}SK_{t-1}$用于偿还本金. 由此, 融资总额的动态关系为$SK_t=SK_{t-1}+U_t-\underline{r}SK_{t-1}$.
在现金管理方面,开发企业现金使用去向包括支付购地费用$B_tP_{Lt}$、开发建设费用$C_{Dt}D_t$、本息偿还$rSK_{t-1}$以及 支付土地持有成本$C_{Lt}(L_{t-1}-D_t)$和可售住房持有成本$C_{Ht}(H_{t-1}-S_t)$,现金来源包括住房销售收入 $S_tP_{Ht}$以及融资$U_t$,现金持有量的动态关系为$K_t=K_{t-1}+U_t+S_tP_{Ht}-rSK_{t-1}-B_tP_{Lt}-C_{Dt}D_t- C_{Lt}(L_{t-1}-D_t)-C_{Ht}(H_{t-1}-S_t)$. 其中,$C_{Dt}=(1+\mu_D)^tC_{D0}$、$C_{Lt}=(1+\mu_L)^tC_{L0}$与 $C_{Ht}=(1+\mu_H)^tC_{H0}$分别为开发企业的单位土地的开发成本以及单位土地和住房的持有成本,$\mu_D$、 $\mu_L$和$\mu_H$分别表示各项成本的增长率,$C_{D0}$、$C_{L0}$和$C_{H0}$分别为各项成本的初值. 假设当期 销售收入发生在期末,不能用于当期购地与开发建设活动,并且当期融资于期末筹集到,不可用于支付当期购地与 开发费用. 则第$t$期土地购买量的约束上限为$B_tP_{Lt}\leq K_{t-1}-rSK_{t-1}-C_{Dt}D_t-C_{Lt}(L_{t-1}-D_t) -C_{Ht}(H_{t-1}-S_t)$.
假设开发企业以目标期(第$T$期末)总利润最大化为经营目标,即max $PRF_T=(V_T-SK_T)-(V_0-SK_0)$. 在给定初值$K_0,L_0,H_0,SK_0$的条件下,该目标函数等价于期末净资产最大化,即max $NA_T=(V_T-SK_T)=K_T+L_TP_{LT}+ H_TP_{HT}-SK_T$. 此外,考虑到开发企业持续经营的目标要求,假设每一决策期开发企业销售总额都应不少于期初总资产的 一定比例$\omega$,即满足$S_tP_{Ht}\geq\omega$$V_{t-1}$. 综上所述,开发企业供给决策的理论模型如下. 目标函数: \begin{equation} \max NA_T=K_T+L_TP_{LT}+H_TP_{HT}-SK_T(1) \end{equation}
决策变量: $U_t,B_t,D_t,S_t,t=1,2,\cdots,T$.
边界条件约束: \begin{equation} \left \{ \begin{array}{ll} S_t\leq H_{t-1}\\ D_t\leq L_{t-1}\\ B_tP_{Lt}\leq K_{t-1}-rSK_{t-1}-C_{Dt}D_t-C_{Lt}(L_{t-1}-D_t)-C_{Ht}(H_{t-1}-S_t)\\ SK_t\leq \beta (K_{t-1}+L_{t-1}P_{L(t-1)}+H_{t-1}P_{H(t-1)})=\beta V_{t-1}\\ S_tP_{Ht}\geq\omega (K_{t-1}+L_{t-1}P_{L(t-1)}+H_{t-1}P_{H(t-1)})\\ U_t,B_t,S_t,D_t,K_t,L_t,H_t,SK_t\geq 0(2)\\ \end{array} \right. \end{equation}
动态关系约束: \begin{equation} \left \{ \begin{array}{ll} H_{t-1}+D_t\eta-S_t=H_t\\ L_{t-1}+B_t-D_t=L_t\\ SK_{t-1}+U_t-\underline{r}SK_{t-1}=SK_t\\ K_t=K_{t-1}+U_t+S_tP_{Ht}-rSK_{t-1}-B_tP_{Lt}-C_{Dt}D_t-C_{Lt}(L_{t-1}-D_t)-C_{Ht}(H_{t-1}-S_t)\\ \end{array}(3) \right. \end{equation}
关键参数动态变化: \begin{equation} \left \{ \begin{array}{ll} C_{Ht}=(1+\mu_H)^tC_{H0}\\ C_{Lt}=(1+\mu_L)^tC_{L0}\\ C_{Dt}=(1+\mu_D)^tC_{D0}\\ P_{Ht}=\theta_t(1+\lambda)P_{H0}\\ P_{Lt}=\eta(\theta_tP_{H0}-(1+\mu_C)^tC_{C0})(1+\delta)\\ \textrm{d}\theta_t/\theta_t=\alpha_\theta\textrm{d}t+\beta_\theta\textrm{d}z(4)\\ \end{array} \right. \end{equation} 2 模型优化求解与企业决策行为的理论分析 2.1 最优化问题求解与企业储备倾向指标构建
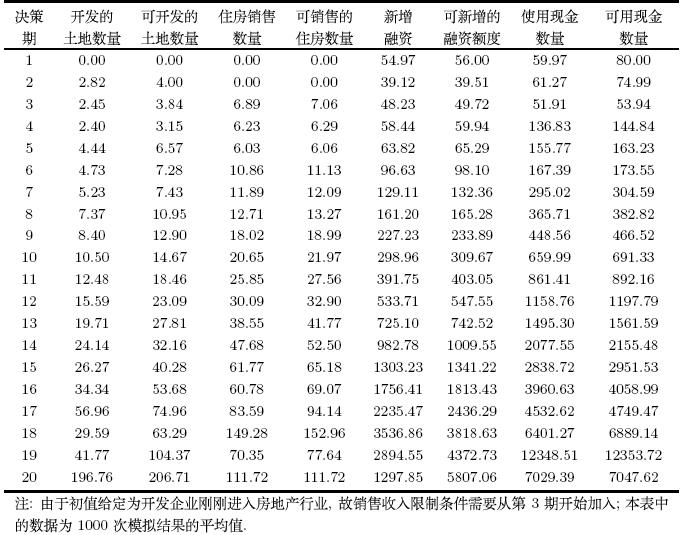
式(1)至(4)所示的理论模型是一个带有价格随机过程的随机优化问题, 可以借鉴文献[7]的方法对该模型进行数值模拟求解,假定初值如表 1所示.
数值模拟结果如表 2所示,反映出开发企业的决策特征如下: 第一, 开发企业具有储备土地的倾向, 不会将期初可开发的土地全部在当期开发建设, 而会根据市场环境与经营阶段,选择合适的储备和开发规模; 第二,类似的,开发企业具有储备可售住房的倾向, 会根据市场情况选择合适的销售进度; 第三, 开发企业具有储备融资额度的倾向, 通常将融资总额控制在低于融资额度上限的水平; 第四, 开发企业具有储备现金的倾向, 不会将所有现金全部用于当期购地与开发经营活动, 而会留存一定比例的现金备用.
数值模拟结果所观测到的开发企业的土地储备、分期开发与销售行为与以单一项目为研究对象所提出的最佳开发与销售策略不同; 观测到的资金管理行为也与以单一决策环节为研究对象的传统观点(最大限度使用融资额度以及最低限度持有现金)不同. 其主要原因在于本文模型中开发企业需要权衡全局, 为了实现持续经营和获取阶段性利润等目标,会牺牲掉部分项目的利益. 这些目标对于开发企业而言也是十分重要的,尤其是上市企业. 因而, 本文提出的供给决策理论模型更加符合开发企业的实际决策情景.
进一步,为了定量衡量开发企业储备倾向的大小,构建四项指标如下: 定义$LR_t=(L_{t-1}-D_t)/L_{t-1}$为土地储备倾向指标, 表示未被开发的土地数量占可开发土地数量的比例; 定义$HR_t=(H_{t-1}-S_t)/H_{t-1}$为可售住房储备倾向指标, 表示未被销售的住房数量占可销售住房数量的比例; 定义$SKR_t=1-(SK_t-SK_{t-1})/(\beta V_{t-1}-SK_{t-1})$为融资额度储备倾向指标, 表示未被使用的融资额度占可用融资额度的比例; 定义$KR_t=(K_t-U_t-S_tP_{Ht})/K_{t-1}$为现金储备倾向指标, 表示未被使用的现金数量占可用现金数量的比例. 基于表 1参数模拟得到各期四项储备倾向指标的均值如图 2所示.
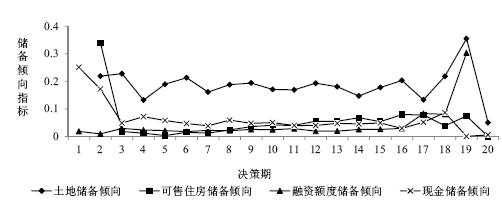 |
| 图 2 开发企业各期储备倾向 |
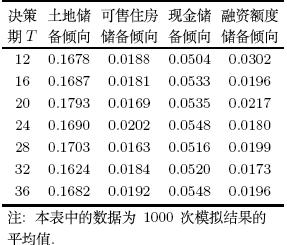
如果改变决策目标期限$T$, 开发企业的储备倾向会发生怎样的变化呢?表 3展示了不同决策目标期$T$下开发企业在稳定经营阶段第4$\sim$9期各储备倾向指标的平均值, 可以看出决策目标期限长短不会显著影响开发企业的储备倾向. 因此, 以持续经营和总利润最大化为目标的常规开发企业的决策行为是稳定一致的. 开发企业在追求更加长期维度的利润增长潜力时, 虽然会牺牲掉部分项目的短期利润, 但这种权衡取舍并不会显著影响到企业短期经营获利的目标. 而实际中, 还存在一些为了短期投机在市场繁荣阶段进入市场的开发企业, 他们以一宗或两宗土地经营的利润最大化为目标, 会具有更强的囤地捂盘倾向, 通过改变理论模型的目标函数也可以对这些投机开发企业的决策行为进行描述.
为了分析开发企业储备倾向的影响因素,本部分进行比较静态分析. 篇幅所限,主要讨论融资限制、融资成本、 房价增长预期和房价风险预期这4项因素的影响效果. 本部分将四个储备倾向指标分为两组,构建两个上级指标: 土地与可售住房储备代表了开发企业的存货储备, 反映开发企业对供给形成的直接影响,定义$SR_t=(L_{t-1}\eta+H_{t-1}- S_t-S_{t+1})/(L_{t-1}\eta+H_{t-1})$为存货储备倾向指标; 现金与融资额度储备代表了开发企业的资金储备,反映开 发企业经营的资金风险,定义资金储备倾向指标为$MR_t=(\beta V_{t-1}-SK_t+K_t-S_tP_{Ht}-U_t)/(\beta V_{t-1}- SK_{t-1}+K_{t-1})$. 汇总分析结果如图 3 所示.
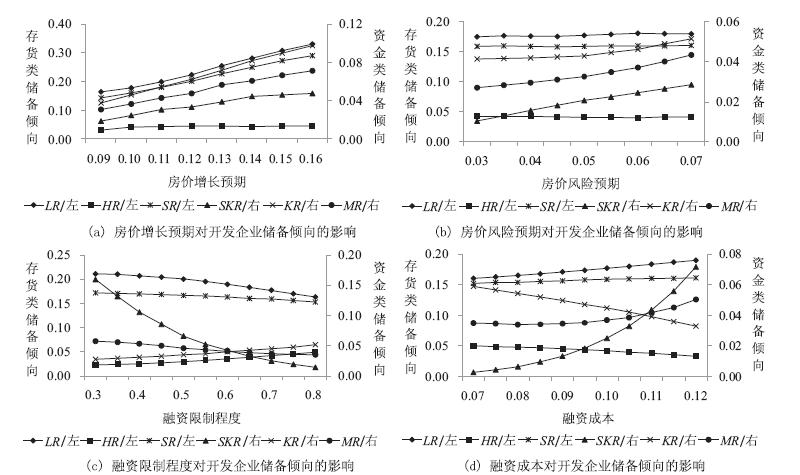 |
| 图 3 开发企业储备倾向的影响因素分析 |
当房价上涨预期增加时,在存货储备方面, 如果建设成本没有发生显著改变, 那么房价上涨预期会快速传导给土地市场, 开发企业在综合考虑多项决策环节的联合决策情境下, 土地储备倾向显著增加,而住房储备倾向几乎没有明显的改变, 总存货储备倾向增加. 在资金储备方面, 现金储备和融资额度储备倾向都有所提高, 企业需要为未来获取项目资源储备更多的资金,但与存货储备相比, 资金储备倾向的增长幅度非常小. 总体上看,如果房价上涨预期增加, 开发企业会更加偏好高存货的策略,市场上会出现更多的"捂盘惜售"现象.
当房价风险增加时, 开发企业对土地与可售住房的储备倾向没有发生显著改变. 而现金储备和融资额度储备倾向都有所提高. 这说明, 面临房价风险水平提高,如果开发企业对房价增长的预期没有发生变化, 那么开发企业的存货储备策略就不会发生显著改变, 即并不急于尽快处理存货资产、降价促销. 此时, 开发企业只要适当提高资金储备, 就足以灵活应对销售收入下降导致的资金短缺问题. 这体现了在市场风险增大时"现金"资产的重要作用, 高风险时期"现金为王"的应对策略, 在2008年金融危机影响过后已经被越来越多的开发企业所认可.
当融资环境趋紧、企业更难获得贷款时,或者当融资成本增加时, 开发企业会小幅减少住房储备, 加快销售、回笼资金,同时也会因为缺少资金而减少开工、提高土地储备, 总体上存货储备倾向小幅提升. 而在资金储备方面, 开发企业会增加现金的使用,减少融资额度的使用, 总体上对资金的储备倾向增强,减少购地和开发活动的资金支出. 这种策略调整行为说明,企业在面临更高融资限制或资金成本的情况下, 虽然为了回笼资金加快销售,短期内可能增加了市场供给, 但长期上却不利于市场上住房供给的形成, 因为开发企业会由于缺乏资金而减少购地和开工支出,增加存货储备, 放缓经营节奏. 3 实证检验
为了验证理论模型的有效性,本部分主要针对两个问题进行实证检验. 1)开发企业的储备行为之间具有显著的相互影响关系,即验证本文构建综合考虑开发企业主要决策环节及其联系的理论模型的必要性. 2)房价预期和融资环境变化对开发企业储备行为的影响效果, 即验证2.2小节比较静态分析结论的合理性. 考虑到2.2小节的分析结论是企业长期的策略调整结果, 并非短期的应急对策, 实证分析需要区分开影响因素的长期、短期影响效果. 综上, 本文选用结构向量自回归模型进行实证检验, 通过脉冲响应函数分析观测房价预期、融资环境变化对企业储备行为的影响以及企业储备行为之间的相互影响效果.
在开发企业储备行为变量选择方面,限于数据可得性, 无法将土地储备和可售住房储备行为分离开,因此选用存货价值率、现金持有比率和负债比率三项指标, 其中负债比率反映融资额度使用情况,与融资额度储备倾向相反. 指标计算方法如表 4所示,需要考虑企业预售行为的影响, 对存货规模、负债、总资产进行调整. 数据来源于Wind 数据库, 遴选企业的标准为证监会行业分类中房地产开发与经营类企业, 要求数据序列完整无误, 研究期内主营业务始终包含房地产开发与经营类业务, 最终选择样本企业30家. 考虑到企业开发经营的季节性变化, 采用4季度移动平均处理方法对原始数据进行季节调整, 最终使用数据时间跨度为2002年4季度至2013年3季度. 为了研究样本企业的总体特征,排除个体影响,实证研究使用30 家企业各项指标的平均数据. 在市场环境变量选择方面, 选用住房价格增长率、住房价格风险以及利率水平三项指标. 其中, 利率水平既反映企业的资金成本,也能够反映企业面临的融资约束情况, 因为当市场利率水平较高时,政府往往采取了紧缩的货币政策, 对企业的融资限制增加. 经过单位根与协整检验,模型系统可以进行回归.
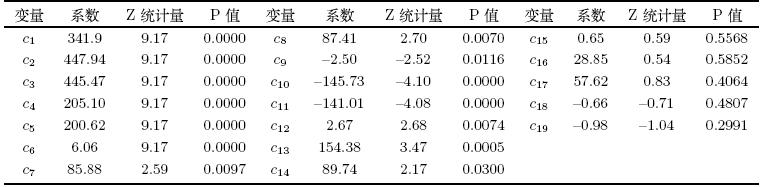
将模型的同期相关约束条件矩阵设定为式(5)形式. 其中,\textbf{\textit{B}}假设为单位矩阵,\textbf{\textit{A}}矩阵中, 三个市场环境变量具有先导性,对企业决策变量施加同期影响; 在三项决策变量中,假设企业的存货决策和现金决策更加主导, 能够对当期的融资决策施加同期影响; 在市场环境变量中,政府制定的利率政策具有先导性,会影响到当期的房价上涨率以及 房价风险. 式(5)约束矩阵总共施加了53个约束条件,大于至少需要设定51个约束条件的目标. 估计得到的矩阵\textbf{\textit{A}} 参数如表 5所示. \begin{equation} \textbf{A}{\varepsilon_t}=\textbf{B}{\mu_t}= \left[ \begin{array}{cccccc} c_1 &0 &0 &c_7 &c_8 &c_9\\ 0 &c_2 &0 &c_{10}&c_{11}&c_{12}\\ c_{16}&c_{17}&c_3 &c_{13}&c_{14}&c_{15}\\ 0 &0 &0 &c_4 &0 &c_{18}\\ 0 &0 &0 &0 &c_5 &c_{19}\\ 0 &0 &0 &0 &0 &c_6\\ \end{array} \right] \left[ \begin{array}{c} \varepsilon_t^{STOCK}\\ \varepsilon_t^{CASH}\\ \varepsilon_t^{LEV}\\ \varepsilon_t^{PRICEG}\\ \varepsilon_t^{PRICER}\\ \varepsilon_t^{RATE}\\ \end{array} \right]= \left[ \begin{array}{c} \mu_t^{STOCK}\\ \mu_t^{CASH}\\ \mu_t^{LEV}\\ \mu_t^{PRICEG}\\ \mu_t^{PRICER}\\ \mu_t^{RATE}\\ \end{array} \right](5) \end{equation}
其中,根据SC最小准则,确定滞后阶数为2; 模型过度识别的似然比检验Chi-2统计量为15.84,在99\%的置信水平下拒绝模型 过度识别假设,说明模型施加53个约束条件是合理的; 存货价值率、现金持有比率和负债比率方程的调整后R$^2$分别为0.99、 0.97和0.98,说明回归模型具有较强的解释能力; 模型稳定性检验中所有单位根的模都小于1,表明模型具有稳定性; 联合Granger因果 检验结果显示所有变量都在95\%的置信水平下显著,表明模型内生结构设置是恰当的; 残差自相关LM检验结果表明,在99\% 的置信 水平下,残差序列不存在自相关性; White异方差检验Chi-2统计量为547.75,P值为0.0868,可以认为模型不具有异方差性.
在以上模型的基础上,通过正交化脉冲响应函数分析, 对三个决策变量之间的相互影响效果以及房价预期、融资环境 变量对储备行为的影响效果进行分析. 图 4和图 5所示的结果表明, 开发企业储备行为之间存在显著的相互影响关系; 而 且面对房价预期和融资环境的变化, 开发企业储备行为的长期响应结果与2.2小节的比较静态分析结果基本一致. 因此,理论 模型的有效性得以验证.
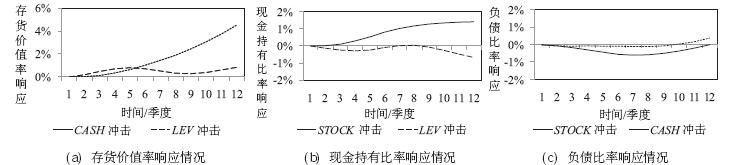 |
| 图 4 开发企业储备行为的相互影响效果 |
 |
| 图 5 开发企业储备行为的影响因素检验 |
本文提出了分析房地产开发企业供给决策的理论模型,该模型能够综合考虑开发企业土地购买与储备、住房开发与销售、现 金与融资管理的主要决策环节,而不限于单一项目或单一决策环节,更加符合开发企业的实际决策情景,具有更强的解释能力.
通过理论分析与实证检验发现: 第一,在一定的市场环境下, 开发企业具有稳定的土地、可售住房、现金和融资额度的储备倾向, 为了实现全局利润最大化与持续经营的目标, 开发企业可能在某一项目或决策环节选择次优策略; 第二, 随着市场环境发生变化,开发企业会对储备策略进行调整,例如, 当房价上涨预期增加时,企业的存货储备倾向显著增强, 当房价风险增加时,企业的资金储备倾向显著增强, 当企业的融资成本增加或受到的融资约束增强时, 开发企业会更多地使用现金并增加融资额度储备, 虽然在短期内为了回笼资金而加快销售, 但长期上开发企业的存货储备倾向增强.
研究结论具有如下实践含义:
对于开发企业而言: 为了谋求长远发展, 开发企业需要权衡项目经营利润与企业扩张能力, 对土地、住房等存货进行合理储备, 避免为了盲目追求项目利润率而过量过长储备存货,影响企业资金周转, 限制长期扩张的能力. 此外, 资金是房地产开发企业一切开发投资活动的基础, 为了应对市场风险、保证企业平稳经营, 开发企业需要持有充足的现金储备以及必要的融资额度储备, 尤其是在市场风险较大的时期.
对于政府调控政策而言: 第一, 由于开发企业具有土地储备与可售住房储备倾向, 政府单纯加大土地供给力度并不一定具有促进住房供给形成的效果, 尤其在房价上涨较快时,开发企业囤地捂盘的意愿更强. 如果想要增加住房供给,还要注意加强对开发企业开发和销售环节的监管. 第二, 政府在出台调控政策以前要注意分析政策对开发企业决策的作用效果, 防止调控结果与初衷背离. 例如, 在提高企业融资成本与融资限制的政策作用下, 虽然短期内开发企业为了缓解资金压力会加快住房销售, 但同时企业也会由于资金短缺而选择放慢开发、购地速度, 提高存货储备倾向. 因此,该政策削弱了企业的长期供给能力, 可能导致长期供求矛盾更加突出,与提高住房供给的政策初衷相违背.
最后需要指出的是,本文提出的理论模型为基础模型, 如果改变"开发企业总体利润最大化"的目标函数, 或对某一决策环节进行细化,或增加约束条件、增加比较静态分析维度, 都能够更加细致地分析开发企业的决策行为及其影响因素, 具有广泛的应用前景.
| [1] | 刘洪玉, 任荣荣. 开发商的土地储备与竞买行为解析[J]. 中国土地科学, 2008, 22(12): 11-16. Liu Hongyu, Ren Rongrong. Research on the behavior of land reserve and land biding of developers[J]. China Land Science, 2008, 22(12): 11-16. |
| [2] | Titman S. Urban land prices under uncertainty[J]. American Economic Review, 1985, 75(3): 505-514. |
| [3] | Somerville C T. Permits, starts, and completions: Structural relationships versus real options[J]. Real Estate Economics, 2001, 29(1): 161-190. |
| [4] | Quigg L. Empirical testing of real option-pricing models[J]. Journal of Finance, 1993, 48(2): 621-640. |
| [5] | Sirmans C F, Turnbull G K, Dombrow J. Residential development, risk, and land prices[J]. Journal of Regional Science, 1997, 37(4): 613-628. |
| [6] | Suen W, Tang B. Optimal site area for high-density housing development[J]. Habitat International, 2002, 26(4): 539-552. |
| [7] | Ott S H, Hughen W K, Read D C. Optimal phasing and inventory decisions for large-scale residential development projects[J]. The Journal of Real Estate Finance and Economics, 2012, 45(4): 888-918. |
| [8] | Ooi J T L, Sirmans C F, Turnbull G K. Government supply of land in a dual market[J]. Real Estate Economics, 2011, 39(1): 167-184. |
| [9] | Lai R N, Wang K, Zhou Y. Sale before completion of development: Pricing and strategy[J]. Real Estate Economics, 2004, 32(2): 329-357. |
| [10] | Chan S H, Fang F, Yang J. Presales, financing constraints, and developers' production decisions[J]. Journal of Real Estate Research, 2008, 30(3): 345-376. |
| [11] | Chan S H, Wang K, Yang J. Presale contract and its embedded default and abandonment options[J]. The Journal of Real Estate Finance and Economics, 2012, 44(1-2): 116-152. |