0 引言
存款保险制度作为维护金融业稳健经营、保护存款人利益的一种手段, 在欧美等发达国家早已实施多年,我国对于存款保险制度的 计划与准备虽已持续了十余年,但迄今为止, 我国仍实行隐性存款保险制度,即若金融机构破产, 央行和地方政府将负责偿还存款人存款. 这种模式不仅给各级财政带来数万亿的负担, 而且也会对金融系统的存款稳定性带来隐患. 正常经济形势下, 当存款人对一国政府保障其利益的程度具有较强信心时, 隐性存款保险制度类似于显性存款保险制度, 能够在一定程度上增强存款人信心,从而使金融系统吸引足够的存款. 当极端经济事件发生情况下,由于存款人利益有明确的保障, 显性存款保险制度能够在一定程度上抑制挤兑现象[1], 而隐性存款保险制度在应对极端经济事件时,表现出更多的不确定性, 如存款保障程度和责任主体的不明晰,因此一旦存款人产生恐慌情绪, 大量存款将可能流出银行系统,从而使金融系统陷入更大的危机. 历史上美国(Countrywide Bank,IndyMac Bank)、英国(Northern Rock Bank)及其他国家的多家银行都曾经历过显著的存款流失现象[2], 期间存款保险制度在一系列重要危机处置计划中发挥了积极作用.
关于银行系统存款流失现象的原因主要有两种观点. 一部分学者认为存款人预期的自我实现性导致了大量存款集中流出银行系统的现象(Postlewaite等[3]; Goldstein等[4]; Rochet等[5]), 即当存款人觉察到其他存款人开始将资金取出银行,会产生焦虑情绪, 进而采取同样的取款行为, 因此众多存款人悲观预期本身就会造成银行的挤兑现象. 另一种观点认为银行存款的流失现象源于存款人处于信息不对称的弱势地位(Jacklin等[6]; Chen[7]; Calomiris等[8]), 由于存款人不了解银行系统的真实运营状况, 一旦得到关于银行基本面的负面消息, 存款人便会质疑银行系统的偿付能力,进而将资金转移出银行系统. 从上述文献中不难看出,研究银行系统的存款稳定性, 存款人信心是需要被关注的重要因素. 存款保险制度在提升存款人信心、维护银行系统存款稳定方面起到了积极作用. Iyer等[2]使用实时更新的存款人提款数据,采用传染病学模型, 研究银行挤兑问题,认为存款保险能够在一定程度上抑制挤兑现象. Prean等[9]研究了金融危机期间增加存款保险保障范围对微观经济产生的影响, 认为在转型国家存款保险制度能够有效提高个人对存款安全和本国货币的信心. Angkinand[10]研究存款保险能否降低银行危机带来的成本, 发现存款保险保障范围较高的国家,具有相对较低的银行危机成本. 目前国外学者对存款保险稳定效应的研究从方法上来看多是实证分析, 而由于我国尚未实行存款保险制度,国内相关研究多停留在理论探讨, 缺少有效的建模及度量手段.
从存款人信念的角度研究存款保险制度的稳定效应, 不可避免要分析作为市场主体的存款人的行为模式, 越来越多的实证证据表明,传统的新古典金融理论并不 能正确反映投资者的实际决策行为和市场运行状况[11]. 正如Miller[12] 所言,未来是不确定和难以预测的, 假设所有人对资产价值有相同估计就不合情理, 不确定性意味着不同的人有不同估计才是合理的, 这种不同估计称为观点分歧(divergence of opinion), 又称异质信念(heterogeneous beliefs), 从而将异质信念引入金融学研究[13, 14]. 金融系统中数以亿计的资金持有者对未来不确定经济环境下银行系统的运行状况, 进而对其存款的期望效用存在认识上的差异, 因此在存款人异质信念前提下研究存款保险的稳定效应是合理的.
本文结合我国隐性存款保险制度的现状,以存款人存在异质信念为前提, 测算正常经济形势下存款保险制度的存款稳定效用, 以及极端事件发生后显性存款保险制度和隐性存款保险制度下银行系统的存款流失率, 进而测算显性存款保险制度相对于隐性存款保险制度在极端事件发生情况下的存款稳定效应. 1 模型的建立 1.1 模型的假设
本文从总量意义上研究存款保险的存款稳定效应, 即研究不同经济环境下总存款流出银行系统的程度与存款保险投保比例的关系, 因此将整个银行系统作为一家银行进行研究. 参考存款保险相关研究及行为金融学的若干模型, 为了降低模型推导的复杂性,本文作出下述简化银行资产/负债价值、市场条件和资金持有者行为的假定. ①银行总资产价值服从含有跳扩散过程的几何布朗运动[15, 16, 17],即
| ${\rm d}V(t)/V(t)=\mu {\rm d}t+\sigma {\rm d}w(t)+(\overline{\kappa}-1){\rm d}Q(t,\lambda)$ | (1) |
其中,$\mu $为正常经济形势下银行资产的即时收益率, $\sigma$为即时收益率的波动率,$w(t)$为布朗运动, $Q(t,\lambda)$是强度为$\lambda$的Possion过程,${\rm d}Q(t,\lambda)$代表极端经济事件引起的收益率跳变. 假设每 次极端事件引起的跳对银行资产价值的影响程度相同, 用$\overline{\kappa}-1$来衡量, $\overline{\kappa}>0$以保证资产价值非负.
②银行负债全部来源于存款,银行为其存款购买存款保险, 投保比例为$\beta$,保险期限与存款期限相同,为$0\sim T$时期;
③市场上仅有一种无风险资产作为银行存款的替代投资渠道, $T$年期存款利率为$r_{d}$,$T$年期无风险利率为$r_{f}$.
④市场上共有$M$个资金持有者, 所有资金持有者在期初0时刻持有相同数量的资金$C$, 并选择将全部资金$C$投资于无风险 资产或者银行存款,在$T$时刻变现.
⑤资金持有者具有相同的幂函数型效用函数$U(x)=x^{\rho}(0< \rho <1)$,资金持有者对于极端经济事件影响银行资 产价值的程度存在意见分歧,且所有资金持有者对极端事件影响参数$\kappa$的估计服从对数正态分布[18].
根据行为金融理论的研究发现, 同一时刻市场上不同资金持有者不仅拥有不同数量和质量的信息, 而且在形成后验信念时也分别受到种类不同、程度不同的认知偏差的影响, 因此同一时刻市场上资金持有者的信念必然存在众多状态, 且当认知对象的不确定性较强时,这种信念的异质现象可能更加显著. 金融系统发生极端经济事件对银行业的影响程度, 不仅受到银行系统内部各种因素的影响, 还与诸如政策因素、国际间风险传染程度等众多因素相关, 因此具有很强的不确定性. 考虑到资金持有者处于信息不对称的弱势地位, 本文对资金持有者对待极端经济事件的态度做出了异质信念的假设. 进一步, 根据大数定理,受到众多因素影响的资金持有者的后验信念应服从正态分布, 而由假设①知, 反映极端经济事件影响程度的参数$\kappa$需满足大于$0$的假设, 因此本文对不同资金持有者$i$的信念参数$\kappa_{i}$取自然对数, 并假设$\ln \kappa_{i}$服从均值为$\overline{\kappa}$、方差为$\theta^{2}$的正态分布.
这一假定是本文核心之处. 若资金持有者对未来不确定性具有同样的信念, 则所有资金持有者将选择同样的投资渠道. 本文认为不同资金持有者对极端经济事件的影响具有不同预期,且满足$\ln \kappa_{i}\thicksim N(\overline{\kappa},\theta)$, 这里$N(\cdot)$为标准正态分布的分布函数,$\theta$表示$\ln \kappa_{i}$的差异程度, 也代表资金持有者对极端经济事件影响程度的意见分歧程度. 在这一假设下,不同资金持有者将根据自己对未来的预期, 决定现在的投资渠道,而银行可以通过购买不同比例的存款保险, 影响资金持有者对银行存款的信心,进而在不同经济环境下稳定存款规模. 1.2 对存款保险保障情况的分析
银行在$0$时刻为其存款购买存款保险,确定投保比例为$\beta$, 如果$T$时刻银行系统出现存款本息的支付困难, 每个存款人可至少获得其存款本息的$\beta$倍. 在保险期末$T$时刻, 保险公司对银行系统的经营状况进行审查. $T$时刻银行资产价值的随机变量为$V(T)$, 银行应支付的存款本息和为$D_{0}\textrm{e}^{r_{d}T}$, 其中$D_{0}$为$0$时刻银行的存款价值. 如果$T$时刻$V(T)\geq D_{0}\textrm{e}^{r_{d}T}$,银行系统经营状况良好, 银行支付存款人$D_{0}\textrm{e}^{r_{d}T}$. 如果$T$ 时刻$V(T)<D_{0}\textrm{e}^{r_{d}T}$,银行出现存款支付困难, 由于未保险存款的偿还顺序优于被保险存款, 当$(1-\beta)D_{0}\textrm{e}^{r_{d}T}\leq V(T)<D_{0}\textrm{e}^{r_{d}T}$时,银行资产将足以偿还其未保险存款, 并能偿还部分被保险存款, 此时存款保险机构承担被保险存款的未被偿还部分, 存款人仍可以获得全部存款本息$D_{0}\textrm{e}^{r_{d}T}$; 当$V(T)<(1-\beta)D_{0}\textrm{e}^{r_{d}T}$时, 银行将只能以其资产价值$V(T)$ 为限偿还部分未保险存款, 而被保险的部分存款$\beta D_{0}\textrm{e}^{r_{d}T}$将全部由存款保险机构代银行偿还, 存款人需承担部分存款损失. 因此$T$时刻所有存款人得到的总存款本息支付额为 \begin{eqnarray}\label{eqn2} \quad \quad D(T)=\left \{ \begin{aligned} D_{0}\textrm{e}^{r_{d}T},\quad \quad \quad \quad &\quad \quad \quad V(T)\geq(1-\beta) D_{0}\textrm{e}^{r_{d}T}\\ \beta D_{0}\textrm{e}^{r_{d}T}+V(T),&\quad \quad \quad V(T)<(1-\beta) D_{0}\textrm{e}^{r_{d}T} \end{aligned}\right.(2) \end{eqnarray} 1.3 对资金持有者行为的分析
对于资金持有者$i$, 在$0$时刻进行投资决策的目的是最大化其$T$时刻收益的期望效用,即 \begin{eqnarray} \nonumber \max \quad E[U(x)]=E(x^{\rho}) \end{eqnarray} 在只有两种投资渠道情况下, 资金持有者在$0$时刻选择包括购买面值为$C$的无风险资产或将资金$C$全部存入银行. 下面将比较这两种投资渠道下$T$时刻的期望效用.
由式(2)知,如选择将资金$C$全部存入银行, 单个资金持有者在$T$时刻能够得到的银行存款本息支付额$d(T)=D(T)/H(\beta)$, 其中,$H(\beta)\leq M$为投保比例为$\beta$情况下, 选择银行存款的总人数,满足$D_{0}=C\cdot H(\beta)$. 由于异质信念的存在, 每个资金持有者对未来$T$时刻可能得到的存款本息存在不同的预期, 在资金持有者$i$信念下,$T$时刻银行对其存款本息的支付额满足 \begin{eqnarray}\label{eqn3} \quad \quad d_{i}(T)=\left \{ \begin{aligned} C\textrm{e}^{r_{d}T},\quad \quad \quad \quad \quad &\quad \quad \quad V_{i}(T)\geq(1-\beta) D_{0}\textrm{e}^{r_{d}T}\\ \beta C\textrm{e}^{r_{d}T}+\frac{V_{i}(T)}{H(\beta)},&\quad \quad \quad V_{i}(T)<(1-\beta) D_{0}\textrm{e}^{r_{d}T} \end{aligned}\right.\quad \quad \quad (i=1,2,\cdots,M)(3) \end{eqnarray} 其中,$V_{i}(T)$为资金持有者$i$信念下$T$时刻银行的资产价值. 为方便计算,以$T$时刻可确定获得的存款本息额$\beta C \textrm{e}^{r_{d}T}$作为参照点,则选择银行存款情况下,资金持有者$i$在$T$时刻的期望效用为 \begin{eqnarray}\label{eqn4} E[(d_{i}(T)-\beta C\textrm{e}^{r_{d}T})^{\rho}](4) \end{eqnarray} 而选择投资无风险资产情况下,资金持有者$i$在$T$时刻的期望效用为 \begin{eqnarray}\label{eqn5} E[(C\textrm{e}^{r_{f}T}-\beta C\textrm{e}^{r_{d}T})^{\rho}]=(C\textrm{e}^{r_{f}T}-\beta C\textrm{e}^{r_{d}T})^{\rho}(5) \end{eqnarray} 对于某些资金持有者满足$E[(d_{i}(T)-\beta C\textrm{e}^{r_{d}T})^{\rho}]\geq (C\textrm{e}^{r_{f}T}-\beta C \textrm{e}^{r_{d}T})^{\rho}$,这些资金持有者将选择将资金存入银行,而其余资金持有者将选择投资无风险资产. \newpage 1.4 均衡的推导
市场中异质信念的存在, 使得不同资金持有者对银行资产价值产生不同预期, 在资金持有者$i$的信念下,银行的资产价值服从 \begin{equation}\label{eqn6} {\rm d}V_{i}(t)/V_{i}(t)=\mu {\rm d}t+\sigma {\rm d}w(t)+(\kappa _{i}-1){\rm d}Q(t,\lambda)\quad \quad \quad \quad (i=1,2,\cdots ,M)(6) \end{equation} 由Dolease-Dade指数公式[19]得到式(6)的解为 \begin{equation}\label{eqn7} V_{i}(t)=V_{0}\cdot(\kappa_{i})^{Q(t,\lambda)}\exp [(\mu -\sigma^{2}/2)t+\sigma w(t)]\quad \quad \quad \quad (i=1,2,\cdots ,M)(7) \end{equation} 则$T$时刻在资金持有者$i$的信念下,银行资产价值满足$\ln V_{i}(T)\thicksim \Phi [\ln V_{0}+Q(T,\lambda)\ln \kappa_{i} +(\mu -\sigma^{2}/2)T,\sigma^{2}T]$,其中$\Phi$为正态分布. 进而在$Q(T,\lambda)=j$条件下,银行资产价值的密度函数为 \begin{eqnarray}\label{eqn8} \nonumber &&f_{j}[V_{i}(T)]=f[V_{i}(T)|Q(T,\lambda)=j]\\ &&\quad\quad\quad\quad=\exp\bigg\{-\frac{1}{2}\bigg[\frac{\ln V_{i}(T)-\ln V_{0}-j\ln \kappa_{i} -(\mu -\sigma^{2}/2)T}{\sigma\sqrt{T}}\bigg]^{2}\bigg\}\bigg/[V_{i}(T)\sqrt{2 \pi }\sigma \sqrt{T}](8) \end{eqnarray} 根据假设①,$Q(T,\lambda)$是强度为$\lambda$的Possion过程,满足 \begin{equation}\label{eqn9} Pr[Q(T,\lambda)=j]=\frac{\lambda^{j}}{j!}\textrm{e}^{-\lambda}(9) \end{equation} 则由全概率公式得到资金持有者$i$信念下,$T$时刻银行资产价值的密度函数为 \begin{equation}\label{eqn10} f[V_{i}(T)]=\sum_{j=0}^{+\infty}f[V_{i}(T)|Q(T,\lambda)=j]\cdot Pr[Q(T,\lambda)=j]=\sum_{j=0}^{+\infty}f_{j}[V_{i}(T)]\frac{\lambda^{j}}{j!}\textrm{e}^{-\lambda}(10) \end{equation} 因此,资金持有者$i$选择银行存款情况下,在$T$时刻的期望效用为 \arraycolsep 2pt \begin{eqnarray}\label{eqn11} \nonumber &&E[U(d_{i}(T)-\beta C\textrm{e}^{r_{d}T})]\\ \nonumber &=&\int_{0}^{(1-\beta) D_{0}\textrm{e}^{r_{d}T}}\bigg[\frac{V_{i}(T)}{H(\beta)}\bigg]^{\rho} f[V_{i}(T)]{\rm d}V_{i}(T)+[ (1-\beta)C\textrm{e}^{r_{d}T}]^{\rho}\int_{(1-\beta)D_{0}\textrm{e}^{r_{d}T}}^{+ \infty}f[V_{i}(T)]{\rm d}V_{i}(T)\\ \nonumber &=&\sum_{j=0}^{+\infty}\frac{\lambda^{j}}{j!}\textrm{e}^{-\lambda}\int_{0}^{(1-\beta) D_{0} \textrm{e}^{r_{d}T}} \bigg[\frac{V_{i}(T)}{H(\beta)}\bigg]^{\rho}f_{j}[V_{i}(T)]{\rm d}V_{i}(T)+\ nonumber &&[(1-\beta)C\textrm{e}^{r_{d}T}]^{\rho}\sum_{j=0}^{+\infty}\frac{\lambda^{j}}{j!}\textrm{e}^{-\lambda}\int_{ (1-\beta)D_{0}\textrm{e}^{r_{d}T}}^{+\infty}f_{j}[V_{i}(T)]{\rm d}V_{i}(T)\\ &=&\bigg[\frac{V_{0}}{H(\beta)}\bigg]^{\rho}\textrm{e}^{(\rho\mu-\frac{\rho-\rho^{2}}{2}\sigma^{2})T} \sum_{j=0}^{+\infty}\frac{\lambda^{j}}{j!}\textrm{e}^{-\lambda}\kappa_{i}^{\rho j}N(h_{j}-\rho\sigma \sqrt{T})+[(1-\beta)C\textrm{e}^{r_{d}T}]^{\rho}\sum_{j=0}^{+\infty}\frac{\lambda^{j}}{j!}\textrm{e}^{-\lambda}[1-N(h_{j})](11) \end{eqnarray} 其中,$h_{j}=[\ln (1-\beta) +r_{d}T-\ln (V_{0}/D_{0})-j\ln \kappa_{i} -(\mu -\sigma^{2}/2)T]/(\sigma\sqrt{T})$. 式(11)的推导见附录. 对于某些认为选择银行存款与无风险资产无差异的中立资金持有者, 存在式(11)与式(5)相等,即$E[U(d_{i}(T)-\beta C\textrm{e}^{r_{d}T})^{\rho}]=(C\textrm{e}^{r_{f}T}-\beta C\textrm{e}^{r_{d}T})^{\rho}$, 令$\kappa^{*}$代表中立资金持有者的信念,则存在 \begin{eqnarray}\label{eqn12} \nonumber &&\bigg[\frac{V_{0}}{H(\beta)}\bigg]^{\rho}\textrm{e}^{(\rho\mu-\frac{\rho-\rho^{2}}{2}\sigma^{2})T}\sum_{j=0}^{+\infty}\frac{\lambda^{j}}{j!}\textrm{e}^{-\lambda} (\kappa^{*})^{j}N(h_{j}^{*}-\rho\sigma \sqrt{T})+\\ &&\quad \quad [(1-\beta)C\textrm{e}^{r_{d}T}]^{\rho}\sum_{j=0}^{+\infty}\frac{\lambda^{j}}{j!}\textrm{e}^{-\lambda}[1-N(h_{j}^{*})]=(C\textrm{e}^{r_{f}T}-\beta C\textrm{e}^{r_{d}T})^{\rho}(12) \end{eqnarray} 其中,$h_{j}^{*}=[\ln (1-\beta) +r_{d}T-\ln (V_{0}/D_{0})-j\ln \kappa^{*} -(\mu -\sigma^{2}/2)T]/(\sigma\sqrt{T})$.
资金持有者$i$的信念值$\kappa_{i}$越大,反映其认为银行受极端事件的负面影响越小或正面影响越大,从而选择银行存款带来的期望效用值也就越大. 故当中立资金持有者信念为$\kappa^{*}$时,所有$\kappa_{i}\geq \kappa^{*}$的资金持有者将选择将资金存入银行. 由$\ln \kappa_{i}$ 服从正态分布,即$\ln \kappa_{i}\thicksim N(\overline{\kappa},\theta)$,得到选择存款保险的资金持有者人数$H(\beta)$占所有资金持有者人数$M$的比例 \begin{equation}\label{eqn13} \frac{H(\beta)}{M} =Pr(\kappa_{i}\geq \kappa^{*})=1-Pr(\kappa_{i}< \kappa^{*})=1-Pr(\ln \kappa_{i}< \ln \kappa^{*})=1-N[(\ln \kappa^{*}-\ln \overline{\kappa})/\theta](13) \end{equation} 联立式(12)、(13)可解得选择银行存款的资金持有者人数$H(\beta)$和中立资金持有者信念$\kappa^{*}$,其中银行在$0$ 时刻的总存款价值$D_{0}=C\cdot H(\beta)$,资产价值$V_{0}=E_{0}+C\cdot H(\beta)$,$E_{0}$为$0$时刻银行的股权价值.
由于每个资金持有者持有相同数量的资金$C$,在投保比例为$\beta$情况下,选择银行存款的资金持有者比例决定了银行存款的规模,即 \begin{eqnarray}\label{eqn14} \eta(\beta)=\frac{C\cdot H(\beta)}{C\cdot M}=\frac{H(\beta)}{M}(14) \end{eqnarray} 其中,$\eta(\beta)$代表银行的存款规模,即银行存款价值总额占市场上资金价值总额的比例. 1.5 存款保险稳定效应分析
我国目前实行的隐性存款保险制度, 在很大程度上依赖于存款人对一国政府的信心. 即虽然没有明确的存款保险合同,但存款人相信,若金融机构破产, 央行和地方政府将负责偿还其存款. 正常经济形势下, 存款人对政府信心较强,隐性存款保险制度与显性存款保险制度类似, 能够产生一定的存款稳定效应. 当极端经济事件发生情况下, 隐性存款保险制度由于没有权责明晰的存款保障措施, 一旦存款人信心动摇,产生恐慌情绪,大量存款将可能流出银行系统.
本节设定两种情境: 正常经济形势和极端经济事件发生后的情形. 分别在两种情境下研究显性存款保险制度和隐性存款保险制度的存款稳定效应. 设定银行对显性存款保险的投保比例为$\beta$, 即在两种情境下显性存款保险均对存款提供比例为$\beta$的保障. 假设正常经济形势下, 存款人认为隐形存款保险也能提供比例为$\beta$的存款保障, 而当极端经济事件发生后, 存款人预期的隐形存款保险保障比例调整为$\beta_{I}$, 且有$\beta_{I}<\beta$.
定义1 正常经济形势下, 存款保险制度(隐性或显性)对银行系统产生的存款稳定效应, 表现为投保前后银行系统存款规模的变化. 投保比例为$\beta$的存款保险的存款稳定效应定义为 \begin{eqnarray}\label{eqn15} \delta(\beta)=\frac{\eta(\beta)-\eta(0)}{\eta(0)}(15) \end{eqnarray} 其中,$\eta(0)$为没有存款保险(投保比例为$0$)情况下银行的存款规模.
假设在存款保险期间开始后极短的时间内发生一次极端事件,且由于极端事件发生频率较低,假设在存款保险期间不会发生第二次极端事件,即有$Q(T,\lambda)=1$. 以$0+$表示极端事件发生的时刻,在$0+$时刻已知$Q(T,\lambda)=1$的情况下,资金持有者将重新考虑是否将其存款取出投资于无风险资产. 由式(8)得到,当$Q(T,\lambda)=1$时,如果将资金继续留在银行,资金持有者$i$在$T$时刻的期望效用为 \begin{eqnarray}\label{eqn16} \nonumber &&E[U(d_{i}(T)-\beta C\textrm{e}^{r_{d}T})|Q(T,\lambda)=1]\\ \nonumber &=&\int_{0}^{(1-\beta) D_{0}\textrm{e}^{r_{d}T}}\bigg[\frac{V_{i}(T)}{H_{N}(\beta)}\bigg]^{\rho}f_{1}[V_{i}(T)] {\rm d}V_{i}(T)+[(1-\beta)C\textrm{e}^{r_{d}T}]^{\rho}\int_{(1-\beta)D_{0}\textrm{e}^{r_{d}T}}^{+\infty}f_{1}[V_{i}(T)]{\rm d}V_{i}(T)\\ &=&\bigg[\frac{V_{0}}{H_{C}(\beta)}\bigg]^{\rho}\textrm{e}^{(\rho\mu-\frac{\rho-\rho^{2}}{2}\sigma^{2})T}\kappa_{i}N(h_{1}-\rho\sigma \sqrt{T})+[(1-\beta)C\textrm{e}^{r_{d}T}]^{\rho}[1-N(h_{1})](16) \end{eqnarray} 其中, \begin{eqnarray}\label{eqn17} \nonumber &&f_{1}[V_{i}(T)]=f[V_{i}(T)|Q(T,\lambda)=1]\\ &&\quad\quad\quad\quad=\exp\bigg\{-\frac{1}{2}\bigg[\frac{\ln V_{i}(T)-\ln V_{0}-\ln \kappa_{i} -(\mu -\sigma^{2}/2)T}{\sigma\sqrt{T}}\bigg]^{2}\bigg\}\bigg/[V_{i}(T)\sqrt{2 \pi }\sigma \sqrt{T}](17) \end{eqnarray} 且$h_{1}=[\ln (1-\beta) +r_{d}T-\ln (V_{0}/D_{0})-\ln \kappa_{i} -(\mu -\sigma^{2}/2)T]/(\sigma\sqrt{T})$,$H_{C}(\beta)$为发生极端 事件情况下仍然选择银行存款的资金持有者人数. 式(16)的推导见附录. 与1.4节的均衡推导类似,首先根据中立资金持有者的效用关系, 即$E[(d_{i}(T)-\beta C\textrm{e}^{r_{d}T})^{\rho}|Q(T,\lambda)=1]=(C\textrm{e}^{r_{f}T}-\beta C\textrm{e}^{r_{d}T})^{\rho}$,得到 \begin{eqnarray}\label{eqn18} \bigg[\frac{V_{0}}{H_{C}(\beta)}\bigg]^{\rho}\textrm{e}^{(\rho\mu-\frac{\rho-\rho^{2}}{2}\sigma^{2})T}\hat{\kappa}N(\hat{h_{1}}-\rho\sigma \sqrt{T})+[(1-\beta)C\textrm{e}^{r_{d}T}]^{\rho}[1-N(\hat{h_{1}})]=[C(\textrm{e}^{r_{f}T}-\beta \textrm{e}^{r_{d}T})]^{\rho}(18) \end{eqnarray} 其中,$\hat{h_{1}}=[\ln (1-\beta) +r_{d}T-\ln (V_{0}/D_{0})-\ln \hat{\kappa} -(\mu -\sigma^{2}/2)T]/(\sigma\sqrt{T})$. $\hat{\kappa}$为此时中立资金持有者的信念. 得到极端经济事件发生情况下,选择银行存款的资金持有者比例为 \begin{equation}\label{eqn19} \frac{H_{C}(\beta)}{M} =Pr(\kappa_{i}\geq \hat{\kappa})=1-Pr(\kappa_{i}< \hat{\kappa})=1-Pr(\ln \kappa_{i}< \ln \hat{\kappa})=1-N[(\ln \hat{\kappa}-\ln \overline{\kappa})/\theta](19) \end{equation}
联立式(18)、(19),可得投保比例为$\beta$时, 极端事件发生后仍然选择将资金存入银行的资金持有者人数$H_C(\beta)$ 和边界信念$\hat{\kappa}$. 进而得到发生极端经济事件情况下银行的存款规模 \begin{equation}\label{eqn20} \eta_{\rm Crisis}(\beta)=\frac{H_{C}(\beta)}{ M}(20) \end{equation}
极端事件发生后银行系统的存款流失率可表示为极端事件发生后银行存款规模的减少比例. 显性存款保险制度下,极端事件造成银行系统的存款流失率可表示为 \begin{eqnarray}\label{eqn21} \xi_{E}(\beta)=\frac{\eta(\beta)-\eta_{\rm Crisis}(\beta)}{\eta(\beta)}(21) \end{eqnarray} 隐性存款保险制度下,极端事件造成银行系统的存款流失率可表示为 \begin{eqnarray}\label{eqn22} \xi_{I}(\beta)=\frac{\eta(\beta)-\eta_{\rm Crisis}(\beta_{I})}{\eta(\beta)}(22) \end{eqnarray}
定义2 极端事件发生情况下,显性存款保险制度的存款稳定效应, 定义为显性存款保险制度与隐性存款保险制度下银行系统存款流失率的差异, 即 \begin{eqnarray}\label{eqn23} \chi(\beta)=\xi_{I}(\beta)-\xi_{E}(\beta)(23) \end{eqnarray} 2 模拟分析 2.1 参数的确定
以我国银行系统作为研究对象,考虑数据的可得性, 选取了十家上市银行作为研究样本,研究期间为2011年度, 计算数据均取自瑞斯数据库.
确定参数的步骤如下:
①利用2011 年各上市银行每日股价及总股本计算出以十家银行为整体的银行系统的每日总股权价值, 进而估计银行系统的即时收益率和波动率;
②根据相关文献给出极端事件发生强度及其对银行影响程度等相关参数的赋值结果;
③以十家银行当前金融市场的均衡状态作为依据确定研究系统中总资金规模及每个资金持有者资金持有量.
由于仅考虑极端事件发生0 或1次的情形,以下计算中$j=0,1$.
1)银行资产收益率与波动率的确定
将$0\sim T$时期分为$n$段,$V_{k}(k=1,2,\cdots ,n)$代表第$k$个时段末银行的资产价值,由假设①知银行在$0\sim T$期间的资产价值满足$\ln V_{k}\thicksim \Phi[\ln V_{0}+(\mu -\sigma ^{2}/2)\sum ^{k}_{\tau=1}h_{\tau},\sigma ^{2}\sum ^{k}_{\tau=1}h_{\tau}]$,其中$h_{\tau}$代表单个时段的时长,$\sum ^{k}_{\tau=1}h_{\tau}$代表前$k$个时段 的总时间长度, 一般以年为单位,经推导可得$E_{k}[\ln (V_{k}/V_{k-1})]=[Q(\sum^{k}_{\tau=1}h_{\tau},\lambda)-Q(\sum ^{k-1}_{\tau=1}h_{\tau},\lambda)]\ln \kappa_{i}+(\mu -\sigma ^{2}/2)h_{k}$,$Var_{k}[\ln (V_{k}/V_{k-1})]= \sigma ^{2}h_{k}$. 由于2011年我国经济运行相对平稳, 没有显著的极端事件引起资产价值发生跳,即有$Q(\sum ^{k}_{\tau=1}h_{\tau},\lambda)-Q(\sum ^{k-1}_{\tau=1}h_{\tau},\lambda)=0(k=1,2,\cdots,n)$, 因此有$E_{k}[\ln (V_{k}/V_{k-1})]=(\mu -\sigma ^{2}/2)h_{k}$. $\ln (V_{k})$的 似然函数为 \begin{equation}\label{eqn24} L_{\ln (V_{k})}(\mu ,\sigma )=-\frac{n}{2}\ln (2\pi)-\frac{n}{2}\ln (\sigma ^{2})-\frac{1}{2}\sum ^{n}_{k=1}\ln (h_{k})-\sum^{n}_{k=1}\frac{[\ln (V_{k}/V_{k-1})-(\mu-\frac{\sigma ^{2}}{2})h_{k}]^{2}}{2\sigma ^{2}h_{k}}(24) \end{equation} 其中,$k=n$时有$V_{n}=V_{T}$. 由于每个时段末银行的资产价值$V_{k}$不可观测,需根据可观测的上市银行股权价值进行估计[20]. 设每时段末银行股权价值为 $S_{k}$,$S_{k}$可看作是一份标的资产为$V_{k}$,执行价格为$D_{T}$的欧式看涨期权的价值,$S_{k}$与$V_{k}$满足 \begin{equation}\label{eqn25} S_{k}=V_{k}N(d_{1,k})-D_{T}\textrm{e}^{-r(T-\Sigma ^{k}_{\tau=1}h_{\tau})}N(d_{2,k})(25) \end{equation} 其中,$d_{1,k}=[\ln (V_{k}/D_{T})+(r_{f}+\sigma ^{2}/2)(T-\sum^{k}_{\tau=1}h_{\tau})]/(\sigma \sqrt{T-\sum ^{k}_{\tau=1}h_{\tau}})$,$d_{2,k}=d_{1,k}-\sigma \sqrt{T-\sum^{k}_{\tau=1}h_{\tau}}$.
由式(25)可得$\partial S_{k}/\partial \ln (V_{k})=V_{k}N(d_{1,k})$,由似然函数式(24)的雅克比变换可得$S_{k}$的似然函数为 \begin{equation}\label{eqn26} L_{S_{k}}(\mu ,\sigma )=L_{\ln (V_{k})}[\hat{V}_{k}(\sigma );\mu,\sigma]-\sum ^{n}_{k=1}\ln \{N[\hat{d}_{1,k}(\sigma)]\}-\sum^{n}_{k=1}\ln [\hat{V}_{k}(\sigma)](26) \end{equation} 其中,$\hat{d}_{1,k}(\sigma )=[\ln (\hat{V}_{k}(\sigma)/D_{T})+(r_{f}+\sigma ^{2}/2)(T-\sum^{k}_{\tau=1}h_{\tau})]/(\sigma \sqrt{T-\sum ^{k}_{\tau=1}h_{\tau}})$,$\hat{V}_{k}(\sigma )$是给定$\sigma $初始值,根据式(25)由$S_{k}$ 反算出的资产价值[21].
计算步骤:
①对资产价值的波动率进行初始赋值$\overline{\sigma }$, 将$\overline{\sigma }$代入式(25)得到$S_{k}$与$V_{k}$的关系式, 根据可测得的$S_{k}(k=1,2,\cdots ,n)$, 得到资产价值的估计值$\hat{V}_{k}(\sigma)(k=1,2,\cdots ,n)$.
②将$\hat{V}_{k}(\sigma)(k=1,2,\cdots ,n)$代入式(26), 进行优化计算,得到第一个波动率的估计值 $\hat{\sigma }_{1}$和收益率的估计值$\hat{\mu}_{1}$.
③再将$\hat{\sigma }_{1}$作为波动率的初始值代入式(25),重复上面过程直到$\hat{\sigma }$和$\hat{\mu}$收 敛.
文献[22]证明了上述估计的一致性和有效性. 由上述极大似然估计方法可知, 银行系统资产价值即时收益率与波动率的估计需要3方面的数据: 银行系统每个交易日的总股权价值、年末的总负债价值和当年的无风险利率. 其中,银行系统每个交易日的总股权价值等于单个银行股权价值之和, 单个银行每日股权价值等于该银行股本与当日股票收盘价的乘积; 总负债价值取各银行每年年末总存款的账面价值之和, 无风险利率取$r_{f}=0.0225$[23]. 具体测算结果见表 1、表 2.
2)其他参数的确定
由于2011年一年期定期存款利率经过三次调整, 一年中共经历四个不同存款利率,分别以不同利率持续时间为权重, 得到加权平均存款利率$r_{d}=0.0287$. 本文借鉴文献[24] 对极端事件及投资者异质信念的研究, 假设银行受极端事件的影响程度$\overline{\kappa}=0.64$, 极端事件发生的强度为$\lambda=0.1$, 资金持有者信念异质程度为$\theta=0.5$. 假设投资者效用函数的幂次$\rho=0.9$. 赋值结果见表 3.
3)总资金规模及资金持有量的确定
当金融体系内部不存在显性存款保险制度时,存款人普遍认为政府会为其存款提供最后保障,即金融系统存在隐性存款保险制度[25]. 由于我国尚未实行显性存款保险制度,且2011年一年期定期存款利率为$0.0287$,略高于无风险利率$0.0225$,这里假设我国当前隐性存款保险制度下,存款保障程度$\overline{\beta}=90\%$. 2011年1月1日银行系统总资产价值$\overline{V}=489472.06$亿元,总存款价值为$\overline{D}=386420.73$亿元,总权益价值$E_{0}=103051.33$亿元. 取总资金持有者人数为当前我国总人口数,即$M=13.5$亿人. 由式(13)、(14)可得目前均衡状态下选择银行存款的资金持有者人数$\overline{H}=13.465$亿人,由$\overline{H}=\overline{D}/C$得到单个资金持有者持有资金$C=\overline{D}/\overline{H}=28697.76$元. 各参数的赋值及计算结果见表 4. 各参数的赋值及计算结果见表 4.
将2.1节确定的各参数代入式(12)、(13), 分别计算得到正常经济环境的均衡状态下, 投保比例分别为0、0.4、0.6和1情况 下对应的银行存款规模, 进而得到不同投保比例下存款保险的存款稳定效应,具体结果见表 5. 正常经济环境下,$\beta=0$时,银行存款完全没有保险, 银行能够吸引的存款规模为$48.76\%$; $\beta=0.4,0.6$时, 银行投保部分存款保险, 银行能够吸引到的存款规模分别为$78.82\%$和$95.01\%$, 存款保险的存款稳定效应分别为$61.65\%$和$94.85\%$; $\beta=1$ 时, 银行存款完全被保险,银行可吸引全部存款,存款稳定效应达到最大, 为$105.09\%$.
取$\beta=0.9$(正常经济形势下存款人默认的隐性存款保险制度下的承保比例, 见表 4),其他参数不变,由式(14)得到正常经济 形式下显性存款保险制度和隐性存款保险制度对应的银行存款规模. 分别把$\beta=0.9$和$\beta_{I}=0.6,0.4,0$代入式(18), 联立式(18)和式(19),得到极端事件发生后, 显性存款保险制度和隐性保险制度下对应的银行存款规模, 进而由式(21)、(22) 计算得 到两种存款保险制度下存款的流失率, 由式(23)得到极端事件发生后, 显性存款保险制度相对隐性存款保险制度的存款稳定效应,具体结果见表 6. 极端事件发生后存款人对其存款保障程度的预期反应了存款人的恐慌程度, 即$\beta_{I}$越小恐慌程度越高. 显性存款保险制度下, 由于有明确的存款承保比例, 极端事件发生后银行系统不会出现大量的存款流失现象, 投保比例为$90\%$情况下,存款流失率仅为$0.01\%$ (当投保比例逐渐下降情况下, 极端事件发生后显性存款保险制度同样保证了较低的存款流失率, 具体结果见2.3节). 隐性存款保险制度下, 即使正常经济形势下存款人对存款保障程度具有良好信心(保障程度$90\%$), 极端事件发生后,一旦出现恐慌,存款人可能将其存款转移出银行体系, 造成较高的存款流失率. 在恐慌程度分别为一般、较强和极强情况下, 对应的存款流失率分别为$7.36\%$、$23.64\%$和$51.60\%$. 显性存款保险制度相对与隐性存款保险制度的存款稳定效应分别为$7.35\%$、$23.63\%$和$51.59\%$.
令$\beta$在$0\sim 1$之间变化, 其他参数不变, 得到正常经济环境下存款保险的存款稳定效应与存款保险投保比例之间的反应趋势, 如图 1所示. 随着存款保险投保比例的增加, 存款保险的存款稳定效应逐渐增加,当投保比例达到$0.8$以上时, 存款保险的稳定效应接近最大并趋于稳定. 同样令$\beta$在$0\sim 1$之间变化(显性存款保险制度下意味着投保比例由小变大, 隐性存款保险制度下意味着存款人在正常经济形势下对银行系统的信心逐渐增强), 假设极端事件发生后存款人产生极度恐慌,即令$\beta_{I}=0$, 其他参数保持不变,得到发生极端事件后, 显性存款保险制度和隐性存款保险制度下银行系统存款流失率的反应趋势, 以及显性存款保险制度相对于隐性存款保险制度存款稳定效应的反应趋势, 如图 2所示. 在不同投保比例下, 极端事件发生后显性存款保险制度均保证了银行系统较低的存款流失率(图 2菱形图标曲线); 当出现极度恐慌时, 隐性存款保险制度下银行系统可能出现明显的存款流失现象(图 2方形图标曲线); 虽然在正常经济形势下, 银行的存款规模随存款人对银行系统信心的增强而增大, 但这可能埋下更大的隐患,即极端事件发生情况下银行系统的存款流失率, 随正常经济形势下存款人信心(隐性存款保险制度下的$\beta$值)的增加而增加; 在各种存款保障比例下, 显性存款保险制度相对与隐性存款保险制度具有较明显的存款稳定效应(图 2三角形图标曲线), 且随投保比例的增加,这种稳定效应更加明显.
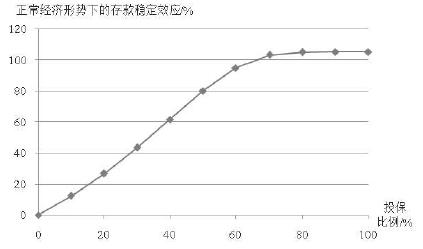 |
| 图 1 正常经济环境下存款保险的存款稳定效应对存款保险投保比例的反应趋势 |
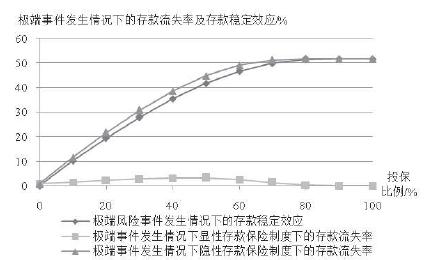 |
| 图 2 极端事件发生情况下显性存款保险制度的存款稳定效应对存款保障比例的反应趋势 |
取存款保险投保比例$\beta=0.6$, 令极端事件发生的强度$\lambda$在$0.05\sim 0.15$之间变化, 其他参数不变, 得到正常经济形势下存款保险制度存款稳定效应的反应趋势, 以及极端事件发生后显性存款保险制度相对于隐性存款保险制度存款稳定效应的反应趋势, 如图 3、4所示. 正常经济环境下,当极端事件发生强度较低时, 存款保险的存款稳定效应维持在$40\%\sim 50\%$之间, 当极端事件发生强度足够大时, 无存款保障情况下银行系统将损失大部分存款, 存款保险的稳定效应出现突然增加,并保持在很高水平; 在极端事件发生强度的各个水平上,极端事件发生后, 显性存款保险制度下银行系统的存款流失率均保持在较低水平(小于$6\%$), 而隐性存款保险制度下银行系统的存款流失率维持在较高水平($50\%$左右), 极端事件发生后显性存款保险制度相对隐性存款保险制度的存款稳定效应保持在较高水平(大于$45\%$).
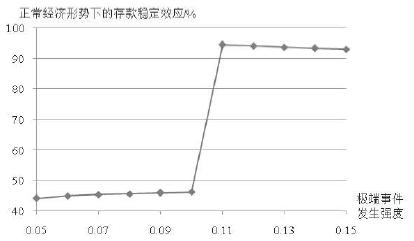 |
| 图 3 正常经济环境下存款保险的存款稳定效应对极端事件发生强度的反应趋势 |
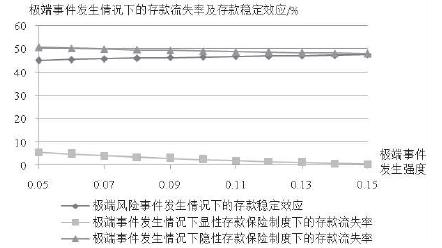 |
| 图 4 极端事件发生情况下显性存款保险制度的存款稳定效应对极端事件发生强度的反应趋势 |
同样取存款保险投保比例$\beta=0.6$, 令资金持有者信念异质程度逐渐增加, 即资金持有者信念的标准差$\theta$在$0.1\sim 1$之间变化, 其他参数不变, 得到正常经济形势下存款保险制度存款稳定效应的反应趋势, 以及极端事件发生后显性存款保险制度相对于隐性存款保险制度存款稳定效应的反应趋势, 如图 5、6所示. 随资金持有者信念异质程度的增加, 正常经济形势下存款保险的存款稳定效应, 以及发生危机后显性存款保险制度相对隐性存款保险制度的存款稳定效应均有一定程度的减少. 由于银行系统的信息透明度在一定程度上会影响资金持有者的信念异质程度, 从而影响存款保险制度的危机稳定效应, 因此增加银行系统的信息公开程度, 有利于存款保险制度发挥存款稳定效应.
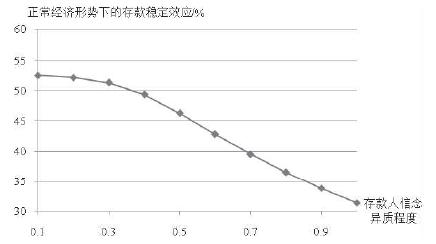 |
| 图 5 正常经济环境下存款保险的存款稳定效应对投资者信念异质程度的反应趋势 |
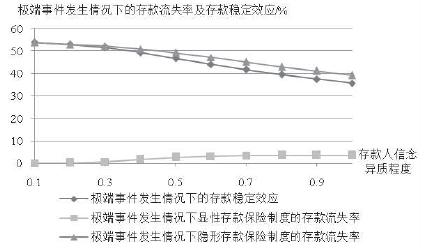 |
| 图 6 极端事件发生情况下显性存款保险制度的存款稳定效应对投资者信念异质程度的反应趋势 |
综合以上,投保比例越高存款保险制度的稳定效应越强; 经济形势越不稳定(极端事件发生强度越大), 存款保险制度的稳定效应越明显;银行系统信息透明度越高, 越利于存款保险制度存款稳定效应发挥作用. 3 结束语
对存款保险制度稳定效应的定量分析有助于更准确地了解存款保险制度在维护金融业稳健发展中所起的作用, 有助于监管机构确定最优的存款保险投保比例及更合理的保险费率. 因此, 本文基于银行资产价值的跳扩散过程, 在存款人异质信念下提出了一种度量存款保险制度的存款稳定效应模型. 模拟分析和灵敏度分析表明: 存款保险的稳定效应与投保比例正相关; 经济形势越不稳定、银行系统信息透明度越高,存款保险的存款稳定效应越显著.
本文研究的问题还存在许多可以继续深入探讨之处. 首先, 模拟分析部分参数的确定参考了国外相关文献, 随着我国存款保险制度的发展及相关数据的完善, 将可能得到更符合我国实际情况的参数,从而增强本文模型的现实意义; 其次, 本文从整个银行系统的角度以总存款规模的变化度量了存款保险的存款稳定效应, 如何在异质信念的市场中,构建不同银行之间的存款竞争模型, 进而在固定利率以及利率市场化的环境下度量存款保险对于单个银行产生的存款稳定效应, 是进一步的研究方向. 另外,除了存款稳定效应外, 存款保险对金融系统产生的稳定效应还有抑制银行破产风险传导等多方面的效应, 本文仅从银行存款规模及存款流失率等角度考察存款保险的存款稳定效应, 其他效应将另文进一步分析.
| [1] | Bruche M, Suarez J. Deposit insurance and money market freezes[J]. Journal of Monetary Economics, 2010, 57: 45-61. |
| [2] | Iyer R, Puri M. Understanding bank runs: The importance of depositor-bank relationships and networks[R]. Cambridge: NBER Working Paper 14280, 2008. |
| [3] | Postlewaite A, Vives X. Bank runs as an equilibrium phenomenon[J]. Journal of Political Economy, 1987, 95: 485-491. |
| [4] | Goldstein I, Pauzner A. Demand deposit contracts and the probability of bank runs[J]. Journal of Finance, 2005, 60: 1293-1327. |
| [5] | Rochet J C, Vives X. Coordination failure and the lender of last resort[J]. Journal of European Economic Association, 2005, 2: 1116-1147. |
| [6] | Jacklin C, Bhattacharya S. Distinguishing panics and information-based bank runs: Welfare and policy implications[J]. Journal of Political Economy, 1988, 96: 568-592. |
| [7] | Chen Y. Banking panics: The role of the first-come, first-served rule and information externalities[J]. Journal of Political Economy, 1999, 107: 946-968. |
| [8] | Calomiris C, Kahn C. The role of demandable debt in structuring optimal banking arrangements[J]. American Economic Review, 1991, 81: 497-513. |
| [9] | Prean N, Stix H. The effect of raising deposit insurance coverage in times of financial crisis——Evidence from Croatian microdata[J]. Economic Systems, 2011, 35: 496-511. |
| [10] | Angkinand A. Banking regulation and the output cost of banking crises[J]. Journal of International Financial Markets, Institutions and Money, 2009, 19: 240-257. |
| [11] | 龚朴, 陈睿. 投资者异质信念下可转换债券赎回策略[J]. 系统工程理论与实践, 2012, 32(3): 656-662. Gong Pu, Chen Rui. Call strategies of convertible bonds under investors heterogeneous belief[J]. Systems Engineering——Theory & Practice, 2012, 32(3): 656-662. |
| [12] | Miller E M. Risk, uncertainty and divergence of opinion[J]. Joumal of Finance, 1977, 32(4): 1151-1168. |
| [13] | 马健, 刘志新, 张力健. 异质信念、融资决策与投资收益[J]. 管理科学学报, 2013, 16(1): 59-73. Ma Jian, Liu Zhixin, Zhang Lijian. Heterogeneous beliefs, corporate financing and investment return[J]. Journal of Management Sciences in China, 2013, 16(1): 59-73. |
| [14] | 陆静, 曹国华, 唐小我. 基于异质信念和卖空限制的分割市场股票定价[J]. 管理科学学报, 2011, 14(1): 13-27. Lu Jing, Cao Guohua, Tang Xiaowo. Stock pricing between segmented capital markets under heterogeneous beliefs and short sale constraint[J]. Journal of Management Sciences in China, 2011, 14(1): 13-27. |
| [15] | Duan J C, Yu M T. Assessing the cost of Taiwan's deposit insurance[J]. Pacific-Basin Finance Journal, 1994, 2: 73-90. |
| [16] | Pennacchi G G. Bank deposit insurance and business cycles: Controlling the volatility of risk-based premiums[R]. Conference Series, Federal Reserve Bank of Boston, 2002. |
| [17] | Mbarek L, Hmaied D M. Deposit insurance and bank risk-shifting incentives: Evidence from the Tunisian banking system[J]. Journal of Money, Investment and Banking, 2011, 20: 41-53. |
| [18] | 张维, 张永杰. 异质信念、卖空限制与风险资产价格 [J]. 管理科学学报, 2006, 9(4): 58-64. Zhang Wei, Zhang Yongjie. Heterogeneous beliefs, short-selling constraints and the asset prices[J]. Journal of Management Sciences in China, 2006, 9(4): 58-64. |
| [19] | 严加安. 鞅与随机积分引论[M]. 上海: 上海科学技术出版社, 1981: 333-343.Yan Jiaan. The introduction of martingale and stochastic integral[M]. Shanghai: Shanghai Scientific and Technical Publishers, 1981: 333-343. |
| [20] | Duan J C, Simonato J G. Maximum likelihood estimation of deposit insurance value with interest rate risk[J]. Journal of Empirical Finance, 2002, 9: 109-132. |
| [21] | 刘海龙, 杨继光. 基于银行监管资本的存款保险定价研究[J]. 管理科学学报, 2011, 14(3): 73-82.Liu Hailong, Yang Jiguang. Study of deposit insurance pricing based on the regulatory capital of commercial banks[J]. Journal of Management Sciences in China, 2011, 14(3): 73-82. |
| [22] | Duan J C. Maximum likehood estimation using price data of the derivative contract[J]. Mathematical Finance, 1994, 4(2): 155-167. |
| [23] | 孙晓琳, 秦学志, 陈田. 监管宽容下资本展期的存款保险定价模型[J]. 运筹与管理, 2011, 20(1): 150-156.Sun Xiaolin, Qin Xuezhi, Chen Tian. Deposit insurance pricing model with capital extension under regulatory forbearance[J]. Operations Research and Management Science, 2011, 20(1): 150-156. |
| [24] | Dieckmann S, Gallmeyer M. Rare event risk and emerging market debt with heterogeneous beliefs[J]. Journal of International Money and Finance, 2013, 33: 163-187. |
| [25] | Angkinand A, Wihlborg C. Deposit insurance coverage, ownership, and banks' risk-taking in emerging markets[J]. Journal of International Money and Finance, 2010, 29: 252-274. |








