Vibration suppression in main drive of rolling mill based on LADRC
0 引言
金属轧制过程中的机电共振、负荷周期性变化以及负载突变产生的系统振荡统称为轧机主传动系统的机电振荡现象.
机电振荡现象 不仅对轧制材料的品质有所影响,
而且会影响控制系统的稳定性[1, 2]. 对于机电振荡的抑制,
控制策略通常是在传统的电流与速度双闭环调节器的基础上进行改进[3, 4, 5].
但是传统控制方法很难在抑制轧制负荷变化带来的扰动和减小连接轴扭矩两方面同时取得良好的控制效果;
且PID直接取目标和实际行为之间的误差,
调节器参数的整定很大程度上依赖于工程经验,难以实现最优[6].
在保证系统调速控制性能的前提下如何有效抑制机电振荡现象,
研究人员在机电模型、控制算法等方面做了许多工作.
文献[7]提出了卡尔曼滤波器极 点配置增强型控制,
改善了系统的瞬态行为,显著降低了系统连接轴冲击扭矩,
但是负载突变时系统动态速降没有得到改善; 文献[8]
提出的神经网络扭矩估计器在系统参数发生变化时能够通过自学习性能调节滤波器的时间常数来获得更好的性能;
文献[9]总结了各类 状态观测器的控制方法,
较好地抑制了扭振和轧制负荷扰动 引起的动态速降,
但是状态观测器对模型参数的依赖性很强,
且参数存在着很大的不确定性和随机的变化. 作为近年来一项热门的技术,
文献[10]将 非线性自抗扰控制系统引入到轧机振动的抑制当中.
非线性控制器由非线性跟踪微分器、非线性ESO和非线性误差反馈控制率构成,
取得了较好的控制效果. 但是非线性的自抗扰控制器设计过程复杂,
需要调节的参数过多,为系统的设计和调节带来很大不便.
相对于非线性控制系统,线性自抗扰控制器设计简单,
控制器参数调节有相对确定的方法,
所以本文将线性自抗扰控制器引入到主传动机 电振荡抑制中.
首先建立从轧机主传动系统两惯性模型中得到系统的微分方程,
然后运用扩张状态观测器重构系统状态变量并实现闭环控制,
最后通过仿真实验 比较了线性自抗扰与传统方法的控制效果.
1 机电系统模型
研究轧机主传动系统的机电振荡问题,多采用文献[5]
中提出的两惯量弹性系统.
轧机主传动两惯量弹性系统的示意图和结构框图分别如图 1和图 2所示.
其中: $T_M$:电机输出电磁转矩; $T_L$:负荷转矩;
$T_{SH}$:轧机连接轴扭矩; $K_{SH}$:联结轴弹性系数;
$\omega_M$:电机旋转角频率; $\omega_L$:轧辊旋转 角频率;
$J_M$:电机转动惯量; $J_L$:轧辊转动惯量; $\theta_M$:电机旋转角 度;
$\theta_L$:轧辊旋转角度.
根据现代控制理论,
可以由传递函数写出轧机两惯量模型的状态方程和输出方程:
| \begin{equation}\label{eq:1}
\begin{cases}
\ \dot{X}=AX+BT_M+ET_L\\
\ Y=CX
\end{cases}
\end{equation} | (1) |
其中$X=[\begin{array}{cccc} \omega_M & \omega_L & T_{SH}
\end{array}]^{\rm T}$,$Y=\omega_M$,
$A=\left[\begin{array}{cccc} 0 & 0 & -\frac{1}{J_M} \\
0 & 0 & \frac{1}{J_L} \\ K_{SH} & -K_{SH} & 0
\end{array}\right]$,$B=\left[\begin{array}{cccc} \frac{1}{J_M}
\\ 0 \\ 0 \end{array}\right]$,$C=[\begin{array}{cccc} 1 & 0
& 0\end{array}]$,$E=\left[\begin{array}{cccc} 0 \\
-\frac{1}{J_L} \\ 0 \end{array}\right]$.
2 线性扩张状态观测器设计
对于式(1),定义$y$为被控对象的输出,$u$为输入且$u=T_M$,
扰动为$w=T_L$,将各个变量代入,就可以得到如式(2)所示的微分方程.
| \begin{equation}\label{eq:2}
\ y'''=-a\dot{y}+bu+c\ddot{u}+dw
\end{equation} | (2) |
其中$a=\frac{K_{SH}}{J_M}+\frac{K_{SH}}{J_L}$,
$b=\frac{K_{SH}}{J_M J_L}$,$c=\frac{1}{J_M}$,
$d=-\frac{K_{SH}}{J_M J_L}$.
式(2)可以改写为
| \begin{equation}\label{eq:3}
\ y'''=-a\dot{y}+(b-b_0)u+b_0 u+c\ddot{u}+dw
\end{equation} | (1) |
令扰动$f=-a\dot{y}+(b-b_0)u+c\ddot{u}+dw$,
包括未知的内扰$-a\dot{y}+(b-b_0)u+c\ddot{u}$和 外扰$w$.
则式(3)可以简写为
| \begin{equation}\label{eq:4}
\ y'''=f+b_0 u
\end{equation} | (4) |
其中$b_0$为$b$的估计参数,是对扰动进行补偿强弱的系数,
在控制器中可以作为一个调节参数使用
[12].
式(4)所代表的被控对象与图 2所示结构框图代表的被控对象是一致的.
前者的表现形式为积分串联,如图 3所示.
令图 3中的输出$y=\omega_M$为状态$x_1$,由图 3写出如下的状态方程组:
| \begin{equation}\label{eq:5}
\begin{cases}
\ \dot{x_1}=x_2 \\
\ \dot{x_2}=x_3 \\
\ \dot{x_3}=x_4+b_0 u \\
\ \dot{x_4}=h \\
\ y=x_1
\end{cases}
\end{equation} | (5) |
其中状态$x_2=\dot{y}$与$x_2=\ddot{y}$分别为轧辊旋转角频率$\omega_L$
和联结轴弹性系数$K_{SH}$; 扩张状态 $x_4=f$为未知扰动,
并用$h=\dot{x_4}=\dot{y}$ 来进行观测和通过状态观测器来进行估计.
则(5)式的状态空间模型为:
| \begin{equation}\label{eq:6}
\begin{cases}
\ \dot{x}=Ax+Bu+Eh\\
\ y=Cx
\end{cases}
\end{equation} | (6) |
其中
$A=\left[\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array}\right]$,
$B=\left[\begin{array}{cccc} 0 \\ 0 \\ b_0 \\ 0
\end{array}\right]$,$E=\left[\begin{array}{cccc} 0 \\ 0 \\ 0 \\
1 \end{array}\right]$,$C=[\begin{array}{cccc} 1 & 0 & 0 & 0
\end{array}]$.
在式(6)的基础上用现代控制理论构造扩张状态观测器,得
| \begin{equation}\label{eq:7}
\begin{cases}
\ \dot{z}=(A-LC)z+Bu+Ly\\
\ \widehat{y}=Cz
\end{cases}
\end{equation} | (7) |
其中被控对象的控制量$u$和输出量$y$都是LESO的输入项,
$L=[\begin{array}{cccc} \beta_1 & \beta_2 & \beta_3 & \beta_4
\end{array}]^{\rm T}$为观测器增益矢量.
由于(7)式的特征多项式为
| \begin{equation}\label{eq:8}
\ s^4+\beta_1 s^3+\beta_2 s^2+\beta_3 s+\beta_4
\end{equation} | (8) |
其中$\omega_o$是状态观测器的带宽. 为了更好地估计状态变量,
应该选取参数$\beta_1$,$\beta_2$,$\beta_3$,
$\beta_4$使得上述特征方程有比较理想的稳定性. 一般来说,
具有形式为$(s+\omega_o)^4$的特征方程具有更好的稳定性,
于是使参数满足公式(9),即可以通过极点配置的方法来获得
[12],
将观测器所有极点均配置在$-\omega_o$处,且$\omega_o$越大时,
观测器越接近于被观测值. 至于取什么样的$\omega_o$
是根据系统带宽的要求确定或在线整定.
| \begin{equation}\label{eq:9}
\ (s+\omega_o)^4=s^4+\beta_1 s^3+\beta_2 s^2+\beta_3 s+\beta_4
\end{equation} | (9) |
所以$\beta_1=4\omega_o$,$\beta_2=6\omega_{o}^{2}$,
$\beta_3=4\omega_{o}^{3}$,$\beta_4=\omega_{o}^{4}$.
经过选择合适的增益参数之后,观测器就能跟踪到各个状态:
\begin{eqnarray*}
\ z_1 (t)\to y(t),z_2 (t)\to \dot{y}(t),z_3 (t)\to \ddot{y}(t),
z_4 (t)\to f(t,y,\dot{y},\cdots,y''',u,\dot{u},\cdots,u''',w).
\end{eqnarray*}
3 线性自抗扰控制律设计
式(4)中被控对象的控制量$u$包含误差反馈量$u_0$和扰动的补偿量两部分,
当观测所得的扰动补偿量基本能够补偿扰动 $f$时,
$y'''$就与$u_0$近似相等,则式(4)又可写为
| \begin{equation}\label{eq:10}
\ y'''\approx u_0=(f-\widehat{f})+u_0
\end{equation} | (10) |
令式(4)和(10)相等,得到控制量
| \begin{equation}\label{eq:11}
\ u=\frac{-\widehat{f}+u_0}{b_0}
\end{equation} | (11) |
因为$x_4=f$,所以式(11)可以改写为
| \begin{equation}\label{eq:12}
\ u=\frac{-z_4+u_0}{b_0}
\end{equation} | (12) |
由式(10)可见,经改造后的控制对象为典型的积分串联型系统,
此类系统在经典PD控制下会达到很好的控制效果. 误差反馈的表达式为
| \begin{equation}\label{eq:13}
\ u_0=k_p(r-z_1)-k_{d1}z_2-k_{d2}z_3
\end{equation} | (13) |
其中$r$为设定值.
注意这里用$-k_{d1}z_2$来代替$k_{d1}(\dot{r}-z_2)$,
用$-k_{d2}z_3$来代替$k_{d2}(\ddot{r}-z_3)$,
以此来避免设定值的微分项,
让闭环传递函数成为无零点的纯三阶形式
[13].
参数$K$可以通过闭环特征方程极点配置的方式来获得,
将极点均配置在$-\omega_c$处,可得
| \begin{equation}\label{eq:14}
\ (s+\omega_c)^3=s^3+k_{d2}s^2+k_{d1}s+k_p
\end{equation} | (14) |
其中$\omega_c$为控制器带宽,$\omega_c$越大时,系统的稳定性越好.
所以$k_p=\omega_{c}^{3}$,$k_{d1}=3\omega_{c}^{2}$,
$k_{d2}=3\omega_{c}$.
根据以上设计结果,系统的线性自抗扰控制器的结构如
图 4所示.
因为被控对象为3阶系统,所以线性扩张状态观测器LESO为4阶,
所扩张的状态为扰动项; 控制器用的是线性PD控制.
系统调节参数主要为$\omega_o$、$\omega_c$和$b_0$.
由经典控制理论可知,若观测器(7)和控制器(10)是稳定的,
则其组成的线性自抗扰系统就是一个有界输入有界输出(BIBO)的稳定闭环系统.
将式(12)和式(13)结合为新的状态反馈:
| \begin{equation}\label{eq:15}
u=(1/b_{0})\left \lfloor -k_{p} -k_{d} -1 \right \rfloor z =Fz
\end{equation} | (15) |
其中$F=(1/b_{0})\left \lfloor -k_{p} -k_{d} -1 \right \rfloor$.
因此闭环系统可以表示为式(16)所示的状态空间方程.
| \begin{equation}\label{eq:16}
\begin{bmatrix}\dot{x}\\ \dot{z}\end{bmatrix}
=\begin{bmatrix}A &\bar{B} \\ LC &A-LC+\bar{B}F\end{bmatrix}
+\begin{bmatrix}
\begin{bmatrix}
\bar{B} & E
\end{bmatrix}\\
\begin{bmatrix}
\bar{B} & 0
\end{bmatrix}
\end{bmatrix}\begin{bmatrix}
r\\ h
\end{bmatrix}
\end{equation} | (16) |
其中$\bar{B}=B/b_{0}$,如果式(16)的特征根在左半平面,
则式(16)为稳定的有界输入有界输出系统(BIBO).
对特征矩阵进行基本行列式变换如式(17)所示.
由式(17)可知所有特征根均位于左半平面. 一般情况下,
系统输入$r$为有界值,
因此仅当系统的不确定量$h=\dot{x_4}=\dot{y}$为有界值时,
系统为稳定系统.
| \begin{equation}
\label{eq:17}
%\begin{split}
{{\rm eig}\bigg(\begin{bmatrix}A &\bar{B} \\ LC &A-LC+\bar{B}F\end{bmatrix}\bigg)} \\
%= eig(\begin{bmatrix}A+\bar{B}F &\bar{B}F \\ 0 &A-LC\end{bmatrix}) \\
%= eig(A+\bar{B}F) \cup eig(A-LC)
%\end{split}
\end{equation} |
| \begin{equation}
= (\mbox{roots of}\ s^{3}+ k_{d2}s^{2}+k_{d1}s+k_{p})\cup(\mbox{roots of}\ s^{4}+ \beta_{1}s^{3}+\beta_{2}s^{2}+\beta_{3}s^{3}+\beta_{4})
\end{equation} | (17) |
4 系统仿真与实验验证
4.1 Simulink仿真
验证所设计控制器性能的系统仿真在Matlab/Simulink 平台上完成.
轧机主传动系统的主要参数 $J_M=0.1766$kg$\cdot $m$^2$,
$J_L=0.1746$kg$\cdot $m$^2$,$K_{SH}=695.567$N$\cdot $m/rad,
$\omega_c=150$rad/s,$\omega_o=500$rad/s.
按照图 4所示的线性自抗扰的原理图在Simulink中建立起控制模型.
0.5s时给定单位阶跃输入; 2.5s时加入负载扰动.
负载扰动用单位阶跃扰动加周期性扰动
的方式$1+0.2\sin(2{\pi}t)$来表示,如图 5中的"负荷扰动"曲线.
图 5中"转速输出值"即为被控对象的输出————电机转子的转速$\omega_M$,
它的调节时间为0.337s(响应到达并保持在终值2%误差内),无超调,
无静态误差; 阶跃扰动时动态速降为2.2%,恢复时间为0.06s;
周期性扰动基本得到完全抑制.
"转速观测值"为扩张状态观测器对于转速输出值的 观测,
从图中可以看出,转速的观测值能够很好地跟随转速输出值,
说明状态观测器重构的各个状态可以很好地复现生产过程中一般情况下不易测得
的状态量.
为了验证线性自抗扰的控制效果,
图 6是与之相比较的传统双闭环控制系统和全维观测器控制系统控制方法的原理框图,
图中SCR为转速调节器,采用 PID控制; CCR为电流调节器,
简化为一阶惯性环节.
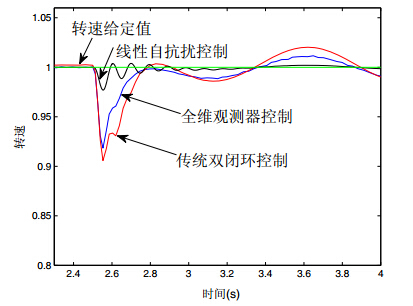
图 7为传统双闭环控制系统、全维观测器控制与自抗扰控制的转速阶跃响应.
传统双闭环控制和全维观测器 控制的PID系数都经过4:1衰减法整定.
传统双闭环控制曲线经过衰减法整定后,
超调量超过了一般工程超调25%的最大限度,手动优化将超调量降至 25%.
全维观测器控制曲线经过参数整定后超调量同样超过了25%,
手动优化参数降低超调,
并保证调节时间与传统双闭环控制调节时间相近以便比较.
经优化后的传统双闭环控制调节时间为0.323s,超调为25%,无静差,
动态速降为8.5%,恢复时间为0.2s. 对于周期性扰动抑制效果一般;
全维观测器 控制的调节时间为0.305s,超调为13.5%,动态速降为4.7%,
恢复时间为0.07s,对于周期性扰动比较好.
发生负载扰动时三种控制策略的动态速降放大 图如图 8所示.
由图 7和图 8中的对比可以看到三种控制方法的调节时间相差不多,
而超调和动态速降方面则有很大差别:
传统闭环控制的动态速降与恢复时间较大,且有明显的周期性波动;
全维观测器在扰动抑制方面有了一定的改进;
而线性自抗扰的阶跃响应无超调,
受到扰动时的动态速降最小,恢复时间最短.
除了转速的动态响应与稳态效果,
连接轴扭矩也是反映轧机主转动机电振荡控制效果的重要指标之一.
图 9所示为三种控制策略下的连接轴上的扭矩$T_{SH}$.
从图 9中可知与双闭环控制相比,
阶跃响应时全维观测器控制引入了更大的负向扭矩,
自抗扰控制则大大减小了此时的尖峰扭矩力; 突加负载时,三种控制
方法下的扭矩变化相差不大,自抗扰控制略有振荡;
对于周期性扰动三种控制方法下扭矩变化也基本相同.
4.2 实验结果
基于以上的设计与仿真结果,
在以TMS320F2812为核心的异步电机调速实验平台上对自抗扰控制系统和传动双闭环控制的性能进行了对比研究,
平台示意图如图 10所示[14].
实验对象电动机的额定功率为2.2KW,额定电压为380V,
额定转矩为15N$\cdot$m,额定频率50Hz,极对数为2,额定转速为1430r/m,
电动机在恒转矩调速区 内,
在2.5s时加入恒定负载转矩和周期性负载转矩$0.4\sin(2{\pi}t)$,
模拟机电振荡. 则传统双闭环控制转速及扭矩响应结果如图 11所示;
自抗扰控制转速及扭矩 响应结果如图 12所示. 图 11(a)和12(a)为转速响应,
图 11(b)和12(b)为连接轴扭矩响应. 电机转速给定经过了斜坡函数作用,
防止冲击 电流对电机造成损害. 速度给定值0.5为标幺值,即为额定转速.
从图中可以看出,与传统闭环控制相比,
线性自抗扰控制在受到扰动时明显减小了动态速降
与恢复时间及连接轴扭矩值.
5 结论
轧机主传动的振荡抑制涉及到多学科诸如轧钢机械、电机、自动化和电力系统等,
因此振荡产生的原因非常复杂. 本文在由主传动机电系
统模型推导的两惯性系统微分方程中引入线性自抗扰控制器,
将扰动项纳入扩张状态观测器重构的系统状态变量,并通过动态误差反馈
控制率实现机电振荡的抑制. 仿真和实验的结果证明,
与传统双闭环控制及全维观测器控制相比,
线性自抗扰控制器能够有效地抑制机电振 荡,
并且改善负载扰动造成的影响,
尤其是显著改善了突发扰动时的动态性能和减低了连接轴上的尖峰扭矩,
同时避免了传统闭环控制和 全维观测器控制中PID调节器本身的缺陷,
具有一定的实用推广价值.