2. 威斯康辛大学密尔沃基分校 工程和应用科学学院 土木工程系, 威斯康辛州 WI 53201
2. Department of Civil Engineering and Mechanics, College of Engineering and Applied Science, University of Wisconsin-Milwaukee, Milwaukee 53201, USA
0 引言
复杂网络是数量巨大的节点及节点间错综复杂的关系共同构成的网络, 复杂网络广泛存在于自然界、生物界、工程界[1, 2, 3, 4, 5, 6]. 较大规模的网络如交通网、航空运输网、电力网以及计算机网等这些表面上形态结构迥异的网络都具有``小世界"、 ``无标度"等复杂网络特征[7, 8, 9], 如网络的平均路径长度较小、聚类系数较大、节点度分布服从幂律分布等, 但又具有各自的动态特性. 目前对复杂网络的研究多集中在网络的拓扑结构、网络博弈[10]、网络同步[11]以及病毒传播等领域. 复杂网络的拥塞问题是一种具有动态特性的复杂现象,随着网络的发展, 网络规模越来越大,网络的应用模式日渐丰富, 计算机网络的拥塞控制问题也日趋复杂. 拥塞控制算法的分布性、网络的复杂性使拥塞控制算法的设计具有很高的难度. 拥塞导致分组丢失率的大幅度提高,端到端的延时急剧加大, 甚至导致整个系统崩溃[12]. 经常出现拥塞且不能及时恢复的网络难以实现良好的QoS保证, 实施拥塞控制是保证信息高效传输以及网络其它QoS 机制正常工作的必要条件[13]. 网络传输能力主要与网络的拓扑结构和路由策略有关, 研究发现网络的连接方式及节点的处理能力、路由方案等对网络的吞吐量有着重要的影响. 但多数通信网络的拓扑结构已经固定了, 对网络拓扑结构的改动几乎是不可能的,因此采用好的路由策略, 提高网络的吞吐量,改善网络拥塞,增强网络的传输能力是比较可行的. 解决网络拥塞的主要方法是通过相应的路由策略在降低数据包时延的同时提高网络的吞吐量. 目前路由策略分为三类: 全局型、局部型与混合型. 全局路由策略需要整个网络的拓扑信息, 局部路由策略只关注临近节点信息,混合路由策略既需要整个网络的信息, 又需要邻近节点信息.
全局路由策略的典型代表是最短路径路由, 数据包从起始节点沿着最短路径到达终止节点, 数据包在一般网络中能很快到达目 的地,但在复杂网络中, 因为最短路径路由算法没有考虑网络的状态, 数据包容易在中心节点处出现拥塞,这些节点的相对介数较大, 是多条最短路径的交汇处, 因此最短路径路由算法将导致介数较大的中心节点处拥塞加剧, 从而导致网络性能的急剧下降[14, 15]. Yan[16] 等提出了改进的最短路径策略,计算最短路径时考虑了节点的度, 有效避免通过度大的节点最短路径过多, 减少了拥塞在这些节点处发生的概率. Slivkins等[17]提出了搜索最邻近节点的 Rings of Neighbors 方法, 提出了基于环的距离近似算法. 刘刚等[18] 提出了一种具有引力约束的路由算法,引入了时间引力和空间引力, 为路由策略优化提供了新思路. 陈华良等[19]提出对网络的每一条边加权的路由策略, 权值与该边的端节点的度相关,该策略提高了网络的传输能力.
由以上分析知,在最短路径路由算法中,中心节点的介数大, 是多条最短路径的交汇处,大量的数据包滞留在介数大的中心节点, 极易导致拥塞. 介数(betweenness)反映了网络中节点的作用和影响力, 比度更能很好地衡量节点在网络中的重要程度. 文献[20] 研究指出分析网络数据流量控制时,节点介数比节点度更重要. 因此, 本文提出一种加权路由策略, 该策略用复杂网络节点的介数作为节点边的权重,将网络变成加权网络. 减少网络在介数大的节点产生拥塞的概率,提高网络的传输效率. 1 网络流量模型及加权路由策略 1.1 网络流量模型
本文采用常见的网络模型: 对于给定的复杂网络,假设网络从无负载开始, 网络上的节点都具有路由、收包、发包等功能, 每一时间步产生的数据包为$R$,源节点和目标节点随机选择, 假设节点的传输能力是相同的,设节点的传输能力为${C_i}$, ${C_i}$是单位时间内每个节点能传递数据包的最大值, 即单位时间内每个节点最多只能发送${C_i}$个数据包, ${C_i}$个数据包自动添加到源节点队尾. 节点的缓存队列长度假设是无限的, 节点传递数据包时首先在邻节点内搜索,如果邻节点中有目标节点, 直接传递给目标节点,同时删除该数据包,如果邻节点中没有目标节点, 数据包根据给定的路由策略传递到下一个节点. 当数据包到达目标节点后, 则删除该数据包. 1.2 加权路由策略
在最短路由策略中数据包从起始节点到终止节点沿着距离最近的路径传输, 经过的节点或边数最少,因此只要起始节点与终止节点确定, 则传输路径是确定的, 通常情况这种策略下的数据包能以最快的速度到达终止节点, 但特别容易在度大的节点上产生拥塞. 原因是最短路由策略下的数据包总是沿着离终止节点最近的路径传输, 没有考虑网络流量分布,也没有考虑网络的状态及网络的吞吐量. 为此本文提出一种基于加权路由策略的拥塞控制机制, 将网络中的边附上权值,权值的大小与该边两端节点介数相关, 通过节点的介数权值达到分流的目的.
对复杂网络中节点的重要度进行评估是非常关键的, 由节点重要度评估出重要的核心节点, 通过重点保护这些核心节点提高整个网 络的可靠性. 节点的度是节点重要度的衡量标准之一[21], 与节点相连的边越多则该节点越重要. 研究表明, 有些重要的``核心节点"并不具有较大的度, 如只有两条边的``桥节点"就是其一. 因此用度评估网络中节点重要度的方法具有片面性. Freeman等[22] 提出介数能更好地衡量节点的重要度, 即经过该节点的最短路径越多则该节点越重要. 因此介数能很好地刻画节点在网络中的重要程度, 但因为早期计算节点的介数较为复杂, 计算节点的介数需要计算节点之间的最短路径, 同时还要记录这些最短路径的路线, 介数计算需要时间复杂性为${O(n^3)}$, 计算的复杂度极大地制约了可计算的网络大小. 节点的介数采用文献${[23]的基于区域中心点近似估算法, 该算法大幅度降低了节点介数的计算复杂度,复杂度降为${O(e+n\log n)}$,${n}$为节点数,${e}$为边数,因此本文采用近似估算法, 该算法在较大的网络中能很快完成计算.
在本文给定的网络模型中, 对源节点${s}$到目标节点${d}$的任意节点${i}$, 其节点介数定义如公式(1)所示.
| \begin{equation} C_B(i)=\sum_{s\neq d\neq i}\partial_{sd}(i), \partial_{sd}(i)= \frac{\partial_{sd}(i)} {\partial_{sd}} \end{equation} | (1) |
公式(1)中,$\partial_{sd} $为节点${s}$到节点${d}$的最短路径数目, $\partial_{sd}(i)$为节点${s}$到节点${d}$的最短路径中经过节点${i}$的最短路径数目.
计算任意节点之间的最短路径的算法复杂度非常高, 因此本文采用文献[23]的CDZ近似算法,对任意节点对${s}$,${d}$, 设${s}$的中心节点为${c_s}$,${d}$ 的中心节点为${c_d}$,则${s}$, ${d}$之间的最短路径可以近似等于由${s}$经 过${c_{s}c_{d}}$到节点${d}$ 的一条路径. 利用该路径即可近似得到$\partial_{sd}$,如公式(2)所示.
| \begin{equation} \partial_{sd}\approx\partial_{sc_{s}}\cdot\partial_{c_{s}c_{d}}\cdot\partial_{c_{d}d}\end{equation} | (2) |
由公式(2)可近似得到$\partial_{sd}(i)$,如公式(3)所示.
| \begin{equation} \partial_{sd}(i)\approx\partial_{sc_{s}}(i)\times\partial_{c_{s}c_{d}} +\partial_{sc_{s}} \times\partial_{c_{s}c_{d}}(i)\times\partial_{c_{d}d}+\partial_{sc_{s}} \times\partial_{c_{s}c_{d}} \times\partial_{c_{d}}(i) \end{equation} | (3) |
由公式(1)、(2)、(3)可近似得到节点${i}$的介数,如公式(4).
| \begin{equation} c_{B}(i)\approx\sum_{s\neq d\neq i}\bigg(\frac {\partial_{sc_{s}}(i)} {\partial_{sc_{s}}}+ \frac{\partial_{c_{s}c_{d}}(i)} {\partial_{c_{s}c_{d}}} +\frac {\partial_{c_{d}d}(i)} {\partial_{c_{d}d}}\bigg)= \sum_{s \in v}\sum_{d \in v}(\partial_{sc_{s}}(i)+\partial_{c_{s}c_{d}}(i)+\partial_{c_{d}d}(i)) \end{equation} | (4) |
设${c}$为中心节点的个数,${n}$为实际节点的个数, 假设每个区域大小基本相同,即$${\partial^{'}_{cs}*(i)}=\sum_{s\in Z(c_{s})}\partial_{sc_{s}}(v)$$
因此只需要计算任意区域${\partial^{'}_{cs}*(i)}$的值,任意两个中心节点之间的最短路径可以进一步简化介数的计算复杂度, 由此近似得到从${s}$到${d}$的任意一点${i}$ 的介数$C_{B}(i)$, 如公式(5)所示.
| \begin{equation} C_{B}(i)\approx \bigg(\frac{n} {c}\bigg)^{2}\sum_{c_{i} \in C}\sum_{c_{j} \in C}\partial_{c_{s}c_{j}}(i)+2n\sum_{c \in C}\partial_{c}*(i) \end{equation} | (5) |
根据文献[23]的仿真估算, 该算法得到的介数的值符合复杂网络的实际计数值,因为复杂网络中节点的 度分布具有幂律特性,网络的中心节点是少量的, 而一般的普通节点占大多数,即$c\ll n$, 算法时间的复杂度仅为$o(e+n\log(n))$.
假设数据包从源节点${s}$到目标节点${d}$的任意一条路径$ p(s,d)$为${s=(\chi_{0},\chi_{1},\cdots,\chi_{n})}$, 该路径上直接连接的节点${i}$,${j}$的介数为${c_{i}}$,${c_{j}}$, 设节点${i}$到节点${j}$的边${e_{ij}}$ 的权重为${w_{ij}}$, ${w_{ij}}$的定义如公式(6)所示.
| \begin{equation} w_{ij}(\alpha,\beta)=c_{i}^{\alpha}\times c_{j}^{\beta}\end{equation} | (6) |
公式(6)的参数${\alpha}$,$\beta $为可调的. 则节点${s}$到${d}$的任一路径${p(s,d)}$的长度为
| \begin{equation} L(P_{j}(s,d))^{(\alpha,\beta)}=\sum_{i=0}^{n-1}w_{i(i+1)}^{(\alpha,\beta)} = \sum_{i=0}^{n-1} (c_{i}^{\alpha} \times c_{i+1}^{\beta}) \end{equation} | (7) |
使公式(7)中$ L(P_{j}(s,d))^{(\alpha,\beta)} $ 最短的路径就是节点${s}$到${d}$的该最短加权路径, 从${s}$到${d}$的数据就沿着最短加权路径传输. 当参数${\alpha=0}$, ${\beta=0}$时,本文的加权最短路径就是传统的最短路径路由策略.
研究表明,在传统最短路径下,网络数据流量较大时, 复杂网络的传输能力较差,因为大量的数据包流向最短路径的交汇处, 直接导致网络的性能急剧下降. 本文基于加权路由拥塞控制策略在网络数据量急剧增大时, 将节点的介数作为连接边的权重考虑在路径里, 这种的路径策略较为均匀地经过各个节点, 尤其在网络拥塞时能及时避免大量的数据涌向介数较大的核心节点. 避免部分重要中心节点的流量过大导致网络拥塞, 该算法充分利用了各个节点的发送能力,有效地提高了网络的吞吐量. 2 仿真与分析
本文的仿真实验选择BA网络模型,其中节点数${N=1000}$, ${m_{0}=m=5}$每次运行5000步, 取50次平均根据最后1000步的平均值确定网络的${R_{c}}$. 网络的负载为${R}$,用状态参数${H}$描述网络拥塞的转变[24]:
| \begin{equation} H(R)=\lim_{t\rightarrow\infty} \frac{1} {R} \frac{P(t)} {t} \end{equation} | (8) |
公式(8)中,$ {P(t)} $是$ {t} $时刻网络中数据包的总个数,使$ {H(R)=0}$的最大$ {R}$是网络的吞吐量,用$ {R_{c}}$表示.
图 1显示了不同的${\alpha}$,${\beta}$策略下网络的吞吐量与节点数${N}$的关系,由实验结果可知${\alpha=0.3}$,${\beta=0.5}$ 时网络的吞吐量是最大的,这与文献[19]基于度的加权策略相一致,即${\alpha=0.3}$,${\beta=0.5}$时路由策略明显优于\\ ${\alpha=0}$,${\beta=0}$以及${\alpha=1}$,${\beta=0}$,此路由策略下网络的吞吐量最大且随着${N}$值的增大一直保持. ${\alpha=0}$,${\beta=0}$ \\ 的传统最短路径,网络的吞吐量随着${N}$的增大变化比较小.
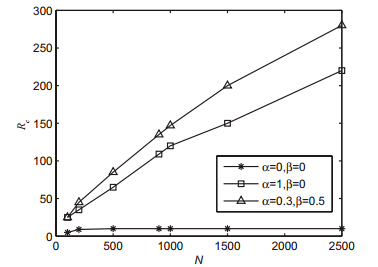 |
| 图 1 ${\alpha,\beta}$取不同值时网络吞吐量与$ {N} $ 的关系 |
原因是传统最短路径下,网络中某些节点的度、介数非常大, 由文献[25]知,网络的传输能力受限于介数最大的节点. 本文采用基于节点介数的加权路由策略,减少最大中心节点的介数值, 充分发挥网络中所有节点的发送能力,充分利用 网络资源, 尤其当网络流量大趋于拥塞时能有效、及时分流, 减少流经介数大的节点的信息流,避免网络核心节点 由于流量大而导致拥塞.
图 2是本文基于介数加权路由策略的吞吐量策略与文献[19]的加权路由策略下网络的吞吐量与${N}$的关系的比较, 取${\alpha=0.3}$,${\beta=0.5}$.
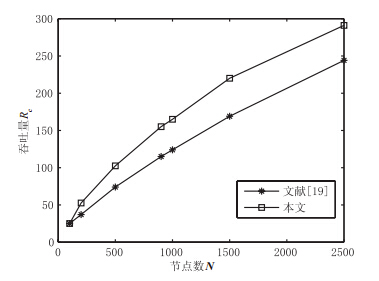 |
| 图 2 不同路由策略下网络吞吐量与$ {N} $的关系 |
由图 2可知,当网络节点数${N}$不太大时, 本文路由策略下的吞吐量与文献[19]基本一致,优势不太明显. 当网络节点数较大时,本文的吞吐量明显大于文献[19], 而且这种优势能持续保持. 原因是文献[19]用度评估网络中节点重要性方法具有片面性, 介数更能体现网络中节点的重要度, 尤其网络节点数较大时对节点重要度的准确衡量更加重要, 基于介数的路由策略能准确挖掘出网络中的``繁忙"节点, 在网络流量急剧向这些节点集中时,将节点的介数权重考虑在路径里, 及时避免了大量的数据流经过``繁忙"节点,避免数据包在这些节点的拥堵, 极大减少网络拥塞的概率,提高了网络的吞吐量.
图 3是本文加权路由策略下当取不同值时平均路径长度与网络节点数的关系.
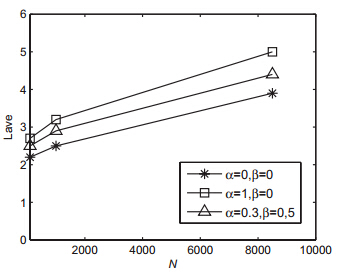 |
| 图 3 ${\alpha}$,${\beta}$取不同值时平均路径与$ {N} $ 的关系 |
由图 3可以看出,加权路径(${\alpha}$, ${\beta}$不全为0)策略下的平均路径长度大于传统的最短路径(${\alpha=0}$, ${\beta=0}$)的平均长度, 本文基于介数的加权策略将节点的介数作为边的权重考虑在路径里, 数据包在传递过程中避开部分拥塞严重的最短路径, 因而平均路径要比传统的最短路径的平均长度增加了一点, 但本文加权路由策略极大提高了网络的传输能力.
图 4是本文与文献[19]不同路由策略下平均路径长度与$ {N} $的关系比较.
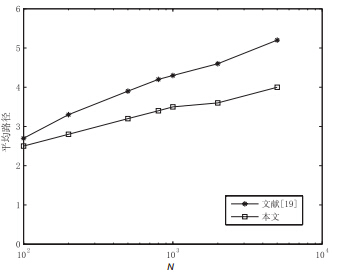 |
| 图 4 不同路由策略下平均路径与$ {N} $ 的关系 |
由图 4知本文的平均路径长度比文献[19]略低一点, 原因是介数能更好地衡量节点的重要度. 节点的介数越大, 经过该节点的最短路径越多, 网络趋于拥塞时本文的路由策略将节点的介数权重考虑在路径里, 避免大量的数据流经网络中真正的``繁忙"节点, 但数据包传递的路径仍是最优的. 当网络中数据流量较大时优势较明显.
图 5是状态参数${H}$随${R}$的变化情况,由仿真结果可以看出,当${R_{c}<R}$,${\alpha}$,${\beta}$取不同值时都 有${H\approx0}$,网络处于平稳状态. 当${R_{c}<R}$时,${\alpha=0.3}$,${\beta=0.5}$的路由策略明显优于${\alpha=0}$, ${\beta=0}$、${\alpha=1}$,${\beta=0}$,其状态参数${H}$的值也在增大,但较为平稳,网络仍处于平衡状态. 而${\alpha=0}$,${\beta=0}$的状态参数迅速增大,网络出现拥塞. 原因是${\alpha=0}$,${\beta=0}$时的 路由策略就是传统最短路径路由,数据包遵循路径长度最短原则,尽管某些节点已经处于严重拥塞,但数据包仍集中 涌向这里,网络中的数据包个数急剧增长,导致这些节点的拥塞情况更加恶化,网络拥塞程度加剧. 当${\alpha=1}$, ${\beta=0}$时,${H}$居于两者中间,${H}$增大较快,但比${\alpha=0}$,${\beta=0}$时增加缓慢.
 |
| 图 5 ${\alpha}$, ${\beta}$取不同值时状态参数${H}$随${R}$的变化情况 |
图 5显示当${\alpha=0.3}$,${\beta=0.5}$时数据包在传递过程中能及时避开拥塞较为严重的关键节点,减轻最短路由算 法中易拥塞的节点的拥塞程度,网络的吞吐量最大,网络的拥塞程度明显降低,这与前面的实验结论一致. 由以上的仿真实 验可以看出,采用基于节点介数的加权路由策略,能避免在介数较大的节点处拥堵,显著提高网络的吞吐量,网络的吞吐 量大于文献[19],路径平均长度稍稍大于传统的最短路径的平均长度,但略小于文献[19],且这种优势能一直保持.
图 6是本文基于介数加权路由策略的吞吐量与文献[19] 在不同规模的无标度子网中的丢包率的仿真实验,取${\alpha=0.3}$, ${\beta=0.5}$.
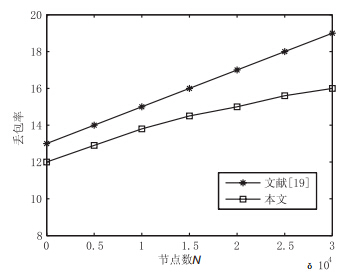 |
| 图 6 不同规模子网中网络的丢包率变化 |
由图 6可知,当网络规模扩大后, 两种算法的丢包率都随着网络规模的扩大而增加,但本文基于介数加权 路由策略的丢包率略低于文献[19]. 原因是本文算法采用中心节点的近似估算,不需要多次划分区域避 免结果的偏置,仅需要选择较少的中心节点,因此网络扩大后, 该算法在BA网络中仍然能较有效避免网络数据拥堵在一些度大的节点上,虽然有丢包现象但整个网络状态稳定. 3 结论
本文提出了一种基于节点介数的加权路由策略, 加权路由策略将节点的介数作为边的权重,将网络变成加权网络. 分析仿真结果,本文的加权路由策略的吞吐量比传统最短路径高几十倍, 并优于文献[19]的路由策略. 平均路径比 传统最短路径大一点, 优于文献[19]. 文献[19]用度评估网络中节点重要性具有片面性, 因为节点的介数比度能更 好地衡量节点的重要度, 早期介数计算由于时间复杂性为${O (n)}$,制约了可计算的网络大小. 本文介数计算采用基 于区域中心点近似估算,计算复杂度大幅度降低, 能够在较大的网络中很快完成计算.
基于加权路由策略优于传统最短路径策略,能有效避免网络数据包集中在个别介数大的繁忙节点而发生拥塞, 网络的传输效率和吞吐量都得到极大提高. 当网络规模扩大后, 该算法在无标度网络中仍然能有效避免大量数据包在关键节点处因拥塞而导致的丢包.
| [1] | Albert R, Barab A L. Statistieal mechanics of complex networks[J]. Reviews of Modern Physics, 2002, 74: 48-94. |
| [2] | 周涛, 柏文洁, 汪秉宏,等. 复杂网络研究概述[J]. 物理, 2005, 34(1): 31-36.Zhou Tao, Bai Wenjie, Wang Binghong, et al. A brief review of complex networks[J]. Physics, 2005, 34(1): 31-36. |
| [3] | 汪秉宏,周涛,何大韧. 统计物理与复杂系统研究最近发展趋势分析[J].中国基础科学, 2005, 7(3): 37-43. Wang Binghong, Zhou Tao, He Daren. The trend of recent research on statistical physics and complex systems[J]. China Basic Science, 2005, 7(3): 37-43. |
| [4] | Wu X J, Lu H T. Generalized projective synchronization between two different general complex dynamical networks with delayed coupling[J]. Physics Letters A, 2010, 374(38): 3932-3941. |
| [5] | 卞秋香,姚洪兴. 复杂网络的线性广义同步[J]. 系统工程理论与实践, 2011, 31(7): 1334-1340.Bian Qiuxiang, Yao Hongxing. Linear generalized synchronization of complex networks[J]. Systems Engineering——Theory & Practice, 2011, 31(7): 1334-1340. |
| [6] | Erdos P, Renyi A. On random graphs[J]. Publications Mathmaticae, 1959, 6: 290-297. |
| [7] | Watts D J, Strogatz S H. Collective dynamics of "small-world" networks[J]. Nature, 1998, 393: 440-442. |
| [8] | Watts D J. Networks, dynamics and the small-world phenomenon[J]. American Journal of Sociology, 1999, 105: 493-527. |
| [9] | Barabasi A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286: 509-512. |
| [10] | Koo J H, Ji D H, Won S C. Synchronization of singular complex dynamical networks with time-varying delays[J]. Applied Mathematics and Computation, 2010, 217: 3916-3923. |
| [11] | Arneas A, Diaz-Guilera A, Kurths J, et al. Synchronization in complex networks[J]. Physics Reports, 2008, 469(3): 93-153. |
| [12] | Nagle J. Congestion control in IP/TCP internetworks[R]. RFC 896, 1984. |
| [13] | 林闯, 单志广, 任丰原. 计算机网络的服务质量[M]. 北京: 清华大学出版社, 2004.Lin Chuang, Shan Zhiguang, Ren Fengyuan. QoS of computer network[M]. Beijing: Tsinghua University Press, 2004. |
| [14] | Liu Z H, Ma W C, Zhang H, et al. An efficient approach of controlling traffic congestion in scale-free networks[J]. Physica A, 2006: 843-853. |
| [15] | 淮存来,裴文江. 一种应用于含权无标度网络的全局路由算法[J].物理学报, 2010, 59(6): 3841-3845.Pu Cunlai, Pei Wenjiang. A global routing method for weighted scale-free networks[J]. Acta Physica Sinica, 2010, 59(6): 3841-3845. |
| [16] | Yan G, Zhou T, Hu B, et al. Efficient routing on complex networks[J]. Physical Review E, 2006, 73: 046108. |
| [17] | Slivkins A. Distance estimation and object location via rings of neighbors[C]// Proceedings of the ACM Symp on Principles of Distributed Computing, Las Vegas: ACM, 2005: 41-50. |
| [18] | 刘刚, 李永树. 基于引力约束的复杂网络拥塞问题研究[J]. 物理学报, 2012, 61(10), 108901.Liu Gang, Li Yongshu. Study on the congestion phenomena in complex network based on gravity constraint[J]. Acta Physica Sinica, 2012, 61(10), 108901. |
| [19] | 陈华良, 刘忠信, 陈增强,等. 复杂网络的一种加权路由策略研究[J]. 物理学报, 2009, 58(9): 6069-6073. Chen Hualiang, Liu Zhongxin, Chen Zengqiang, et al. Research on one weighted routing strategy for complex networks[J]. Acta Physica Sinica, 2009, 58(9): 6069-6073. |
| [20] | 陈关荣.复杂网络及其新近研究进展简介[J]. 力学进展, 2008, 38(6): 653-662.Chen Guanrong. Introduction to complex networks and their recent advances in mechanics[J]. Advances in Mechanics, 2008, 38(6): 653-662. |
| [21] | Callaway D S, Newman M E J, Strogate S H, et al. Network robustness and fragility: Percolation on random graphs[J]. Physical Review Letters, 2000, 85(25): 5468-5471. |
| [22] | Freeman L C. A set of measures of centrality based upon betweenness[J]. Sociometry, 1977, 40(1): 35-41. |
| [23] | 唐晋韬, 王挺, 王戟. 适合复杂网络分析的最短路径近似算法[J]. 软件学报, 2011, 22(10): 2279-2290.Tang Jintao, Wang Ting, Wang Ji. Shortest path approximate algorithm for complex network analysis[J]. Journal of Software, 2011, 22(10): 2279-2290. |
| [24] | Arenas A, Diaz-Guilera A, Guimera R. Communication in networks with hierarchial branching[J]. Physical Review Letters, 2001, 86(14): 3196-3199. |
| [25] | Guimera R, Diaz-Guilera A, Vega-Redondo, et al. Optimal network topologies for local search with congestion[J]. Physical Review Letters, 2002, 89, 248701. |


