2. 南京航空航天大学 民航学院, 南京 210016;
3. 上海工程技术大学 航空运输学院, 上海 201620
2. College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
3. College of Air Transport, Shanghai University of Engineering Science, Shanghai 201620, China
0 引言
故障风险通常是用故障可能性(即故障发生概率)和故障严重性表示的. 风险评估(risk assessment)是根据故障发生的可能性及后果的综合评定. 故障风险评估是对故障带来的危险进行可能性与严重性分析, 然后确定危险的风险等级. 从以可靠性为中心的维修(reliability centered maintenance,RCM)的概念表明,系统故障的影响是多方面的, 因此对故障进行风险评价时,不应以单一因素作为评价目标, 应当同时考虑故障造成的多方面影响,整合多方面的信息, 这样才能使评估更为科学和全面. 开展故障风险评估方法研究不仅能对系统故障风险的可能性、严重性有较为直观的认识, 还能为系统的安全性分析提供支持.
在航空航天领域现有的故障风险评估方法中, 风险优先数法[1]和危害性矩阵法[2]作为较成熟的故障风险评估方法, 有着广泛的应用. 文献[3, 4, 5, 6, 7]也给出了风险评估的定量计算方法, 但是这些方法一方面采用的故障发生概率为长期统计平均值, 不能实时反映外部环境、运行工况对故障发生概率的影响, 使其在进一步实际应用中成为困难, 另一方面这些方法孤立地分析一个故障模式, 未考虑其可能后续故障的风险水平,致使评估结果缺乏系统性、准确性, 解决这两个问题的关键在于要求模型有较强的演变解释能力, 使得可以基于模型进行故障劣化趋势预测,明确故障模式的发展变化过程. 符号有向图(signed directed graph, SDG)模型\,[8]能根据运行工况实时调整, 为解决第一方面运行工况的问题提供了一个很好的平台, 而第二个方面的问题的改善主要在于辨识故障模式的传播发展过程, 并能系统地分析整个故障发展、演变过程中的风险. 因此, 对于一个故障模式,如何实现整体和部分相结合的风险评估, 形成民机风险评估方法体系,能更有效地提高故障风险能力, 是目前开展故障风险评估的重点也是难点.
民机系统运行过程中,由于各项指标或影响因素不断发生变化, 评估故障风险所需的各种指标不容易确定, 故障后果的严重度和风险因素大小更是难以量化. 在飞机故障风险评估过程中, 不仅存在着确定性因素,同时也具有很多不确定信息. 另外, 实际应用中往往无法获取完整的飞机系统状态信息, 也导致评估数据或评估依据不充分的问题. 上述这些情况都被称为"灰". 灰色系统模型对样本数据并无严格的要求或限制, 样本的分布情况也不是计算的必备条件,因而应用广泛,使用灵活. 针对民机系统往往信息缺乏、故障风险因素的灰色性和难以量化的问题, 本文在基于SDG模型隔离故障链和生成故障树的基础上, 提出一种灰色聚类决策的风险综合评估方法,通过将故障模式看作灰色系统, 采用灰色聚类决策方法实现了对故障模式的评估. 1 基于SDG的故障链隔离和故障树的生成
SDG模型[9]是一种典型的DG(有向图)模型. 虽然SDG模型只是定性而非精确的定量模型,然而SDG 通过变量的定向符号能有效地描述了系统的机理和关系. SDG的思想萌芽于20世纪70年代,但其理论与应用的研究是在Iri M等人提出SDG数学定义的70年代末才真正兴起的. 1979年, Iri等人[10, 11] }$首次定义了符号图并在化工领域运用基于深度优先的算法处理静态不完全的符号图样本. 30多年来,SDG模型及相关故障诊断方法日趋完善. SDG模型中的元素表示能力不断增强, 节点和有向边的状态不再局限于有限的几个状态, SDG承载的信息量逐渐增加. 国内SDG研究也获得了较大的发展, 杨帆等[12]对SDG建模及其应用进行了总结并深入研究了其中的热点问题. 南京航空航天大学的周虹[13]研究了基于TMSDG的民用飞机故障诊断隔离策略. SDG的优点在于它可以清楚地描述系统中的各局部、各变量间的因果关系, 能解释故障及危险的传播路径从而为故障诊断提供模型依据.
故障树分析法(fault tree analysis,FTA)是一种有效的系统可靠性分析方法. 对于复杂系统而言,开展故障树的生成研究至关重要. 本文在前人研究的基础上, 通过基于SDG模型隔离故障链和生成故障树,明确故障模式的发展变化过程, 然后以故障因果链为分析对象实现整体和部分相结合的故障风险评估. 1.1 基于SDG模型的故障链隔离
本文中的故障链由初始事件、延续事件及后果事件构成. 其中初始事件是指一个待评价的故障模式,是模型中的一个故障源节点, 延续事件是对初始事件发挥直接作用的节点, 而后果事件是对初因事件发挥间接作用、发生在延续事件之后的节点. 层次有向图描述了系统故障从高层节点传播到底层节点的层次结构,因此, 本文中的故障链是指故障的发展顺序, 故障节点从低层次到高层次依次排列. 为简化分析, 本文将故障链的传播规定为: 如果某节点发生后不能被监测或观测到, 则延续节点才有可能发生,如果某节点发生后能够被监测或观测到, 则本文假定该节点的故障影响一定能够通过某些措施加以控制, 阻止其进一步传播,故将该节点认为是故障链的终止节点. 在SDG模型中, 若一个节点有与之相关联的测试属于状态监测类型, 认为该节点是可监测的,否则认为该节点是不可监测的节点. 本文针对已识别的故障模式,隔离出以该故障模式为初始事件的故障链, 明确故障模式的发展变化,识别该故障可能导致的后果, 并以故障链作为评估对象, 用风险表示故障链中各故障发生的概率和后果的综合量度, 预测故障劣化趋势,系统化地分析故障模式的发展变化中的风险, 实现整体和部分相结合的故障风险评估. 1.2 基于SDG模型的故障树生成
本文用故障树分析故障链中初因事件和延续事件的原因, 计算这些事件的可能性. 故障树分析是一种反向推理过程, 把故障链中的延续事件(称为顶事件)作为分析起点, 将导致事故的原因事件按因果关系逐层列出. 基于SDG模型生成故障树具体步骤为:
1)找出模型中所有的回路并判断回路类型, 用单独一个节点来表示强连通部分而得到压缩有向图.
2)只取状态节点及其关联关系,构成层次SDG模型[14], 表示故障源的层次.
3)选取系统的故障事件,即顶节点. 对于图论模型来说, 这个顶事件也就是图模型中的某个取值为非0的节点.
4)以顶节点事件和边界发生的条件为瞬时样本, 通过反向推理在SDG模型中确定其导致事件发生的原因节点.
5)针对 SDG模型中的原因节点, 根据原因节点的类型选取对应的操作符连接原因节点, 并进一步对回路节点展开因果关系树. 2 灰色聚类的基本概念
灰色系统是指部分信息明确、部分信息不明确的系统, 即信息不完全的系统. 信息不完全是指系统因素、因素关系、系统结构及系统作用原理等方面信息的缺乏. 灰色系统理论是以"部分信息已知、部分信息未知"的"小样本"、"贫信息"的不确定性系统为研究对象[15], 主要通过对"部分"已知信息的生成和开发,提取有价值的信息, 实现对系统运行行为的正确认识和有效控制. 风险评估因素中有些是可以量化的,有些则不可以量化,有确定性信息, 也存在着许多不确定信息. 所有这些情况可归结为信息不完全, 即"灰"[16].
影响故障模式的风险因素有很多,如可靠性、安全性方面的因素. 这些因素都是定性的、模糊的、非数值的、很难进行量化. 通过提取系统中部分已知信息获取有价值的信息,进而确定系统蕴含的未知信息. 灰色聚类决策按照多个不同的决策指标对决策对象进行综合评价, 以便对决策对象进行分类和选优.
定义1 设有$n$个聚类对象,$m$个聚类指标,$s$个不同灰类, 决策对象$i$关于决策指标$j$量化评价值为$x_{ij}$ $(i = 1, 2,\cdots,n; {j}={1},{2},\cdots,{m} )$,$f_j^k (x_{ij} )(j=1,2,\cdots,m;k=1,2,\cdots,s)$为决策指标$j$关于$k$灰类的白化权函数, $w _j $为决策指标$j$的聚类权,$\sum_{j=1}^m {w _j } =1$, 则决策对象$i$在$k$灰类下的决策系数为
| \begin{equation} \label{eq1} \sigma _i^k =\sum\limits_{j=1}^m {f_j^k } (x_{ij} )w _j \end{equation} | (1) |
定义2 称$\sigma_i = (\sigma_i^1,\sigma_i^2,\cdots, \sigma_i^s) (i = 1,2,\cdots,n)$为决策对象$i$的决策系数向量, 则决策系数矩阵为
| \begin{equation} \begin{bmatrix} \sigma_1^1 & \sigma_1^2 & \cdots & \sigma_1^s \\ \sigma_2^1 & \sigma_2^2 & \cdots & \sigma_2^s \\ \vdots & \vdots & & \vdots \\ \sigma_n^1 & \sigma_n^2 & \cdots & \sigma_n^s\\ \end{bmatrix} \end{equation} | (2) |
故障风险评估的过程如图 1所示,以故障模式的故障链为分析对象, 首先确定分析指标,配置影响因素权重,采用灰色聚类算法计算风险度, 最后综合 故障链的风险度,得到风险等级.
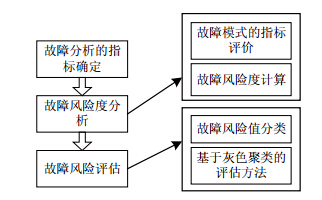 |
| 图 1 基于灰色聚类的故障风险评估过程 |
具体的故障风险评估步骤为:
步骤1 确定风险评估指标体系
民机产品的特殊性决定了民机故障模式风险的确定是一个考虑多因素的复杂决策过程, 传统 FME- A 风险分析用风险等级表示综合评定的风险值, 通常以故障后果的严重度及故障的发生概率来衡量风险等级, 本文选取发生度、影响度和难检度为影响故障风险度的一级影响指标, 其中发生度是指故障的出现频率或发生的概率, 影响度是指发生的故障对飞机系统的影响程度, 难检度是指在当前测量条件和手段下探测故障失效因素的机会或难易程度. 进一步选取故障率为发生度的二级影响指标, 环境安全性、维修费用、停运时间为影响度的二级影响指标, 状态突发性、状态测量费用为难检度的二级影响指标, 各二级影响指标的底层指标为故障模式, 最终形成的故障风险评估指标体系如图 2所示.
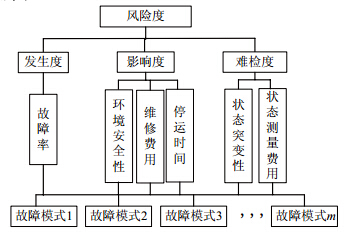 |
| 图 2 故障风险评估指标体系 |
步骤2 设定评估灰类及白化权函数
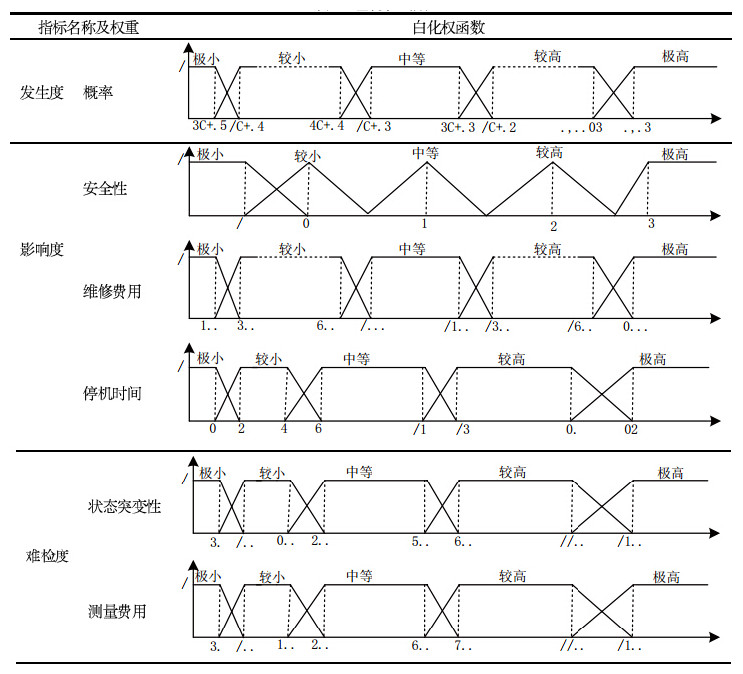
灰类数$s$的划分参照综合评价的要求, 将图 2故障风险评估指标体系中的二级影响指标的取值范围划分为对应的$s$个评估灰类, 假设对象$g$是第$i$个一级影响指标对应的二级影响指标$j$的样本值, $x_{igj}$是$k$灰类的白化权函数. $f_{ij}^k(x_{igj})(j=1,2, \cdots,m; k = 1,2,\cdots,s).$ 有四类典型的白化权函数(如图 3所示). 图中$A$、$B$、 $C$、$D$为转折点,分别是:
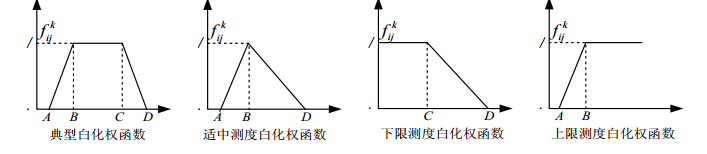 |
| 图 3 典型的白化权函数 |
典型白化权函数$f_{ij}^k[A,B,C,D]$: 当样本值$x_{igj}$在$B$与$C$之间时,对象$g$则完全属于$k$子类;
适中测度白化权函数$f_{ij}^k[A,B,-,D]$: 当样本值 $x_{igj} = B$时,对象$g$则完全属于$k$子类;
下限测度白化权函数$f_{ij}^k[-,-,C,D]$: 当样本值$x_{igj}$减少到$C$以下,对象$g$则完全属于$k$子类;
上限测度白化权函数$f_{ij}^k[A,B,-,-]$: 当样本值$x_{igj}$必须达到$B$以上,对象$g$则完全属于$k$子类.
步骤3 确定聚类指标权重
根据上文确定的故障风险评估指标体系,二级发生度聚类权向量 $w_1=[1]$,还需要确定一级指标聚类权向量$w$、二级影响度标聚类权向量 $w_2$和难检度聚类权向量 $w_3$. 由于各因素的衡量单位和尺度不一致, 同时鉴于风险度对权重的高敏感性, 可引入AHP法计算各因素的权重[17], 具体确定方法和过程不在本文的研究范围之内.
步骤4 确定故障链评估样本矩阵
设故障链中包含$m$个事件, 记第$g$个事件的$U_{ij}$指标(一级指标$i$下的二级指标$j)$值为$x_{igj}$, 对每个事件的指标进行统计或计算, 可得到三个一级影响指标的评估样本矩阵$X_i$.
| \begin{equation} X_i = \begin{bmatrix} x_{i11} & x_{i12} & \cdots & x_{i1n} \\ x_{i21} & x_{i22} & \cdots & x_{i2n} \\ \vdots & \vdots & & \vdots \\ x_{im1} & x_{im2} & \cdots & x_{imn} \\ \end{bmatrix} \end{equation} | (3) |
步骤5 计算灰色评估值
1) 计算事件$g$针对指标$U_{ij}$属于第$k$个灰类的灰色评估系数$f_{ij}^k(x_{igj})$, $g$事件灰色评估权向量计算公式如下:
| \begin{equation} f_{ij}(x_{igj}) = (f_{ij}^1(x_{igj}), f_{ij}^2(x_{igj}),\cdots,f_{ij}^k(x_{igj})) \end{equation} | (4) |
将$U_i$包含的下级指标$u_{ij}(i = 1 \sim 3; j = 1\sim n_i)$的灰色评估权向量$f_{ij}(x_{igj})$构成事件$g$对于指标$U_i$的灰色评估量矩阵
| $R_{ig}$: \begin{equation} R_{ig} = \begin{bmatrix} f_{i1}(x_{igj}) \\ f_{i2}(x_{igj}) \\ \vdots \\ f_{in}(x_{igj}) \\ \end{bmatrix} = \begin{bmatrix} f_{i1}^1(x_{ig1}) & f_{i1}^2(x_{ig1}) & \cdots & f_{i1}^k(x_{ig1}) \\ f_{i2}^1(x_{ig2}) & f_{i2}^2(x_{ig2}) & \cdots & f_{i2}^k(x_{ig2}) \\ \vdots & \vdots & & \vdots \\ f_{in}^1(x_{ign}) & f_{in}^2(x_{ign}) & \cdots & f_{in}^k(x_{ign})\\ \end{bmatrix} \end{equation} | (5) |
2) 对指标$U_i$所包含的二级指标进行综合评估,结果记作: \[ b_{ig} = w_iR_{ig}. \]
3)实现一级指标的评估: 基于总指标$U$中的一级指标$U_i$进行计算, 评估事件$g$的风险灰色聚类决策系数结果为:
| \begin{equation} \sigma_g = w \begin{bmatrix} b_{1g} \\ b_{2g} \\ b_{3g} \\ \end{bmatrix}=\begin{bmatrix} \sigma_g^1 & \sigma_g^2 & \cdots & \sigma_g^k \\ \end{bmatrix} \end{equation} | (6) |
4) 在风险灰色聚类评估结果向量$\sigma_g$计算故障链的综合风险值, 计算公式如下:
| \begin{equation} \eta_g = \sum^n P_k * \sigma_g^k \end{equation} | (7) |
以故障链的综合风险值 为划分依据,故障模式的取值范围如表 1所示.
民机发动机引气系统包含了若干故障模式, 本文选取其中的"PRSOV开在关位"、"PRSOV调节压力偏大"及"预冷器性能降低"三个故障模式为例, 应用本文提出的基于SDG和灰色聚类决策的故障风险评估方法.
1)首先,建立以三个故障模式为起因事件的故障链.
依据本文1.1节的方法将SDG模型隔离出三个故障模式的传播链. 三个故障模式属于引气调节与控制子模块, 重构引气调节与控制子模块及其可达模块---监控子模块的相关节点的有向图, 并进行分层,得到故障传播层次结构如图 4所示.
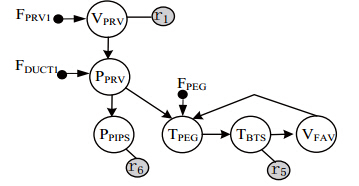 |
| 图 4 故障分层传播 |
图 4中用符号$\bigcirc$表示状态变量节点, 表示测试节点,
V表示阀门开度,F表示流量,P表示压力,T表示温度.
由于"PRSOV卡在开位"对应的状态节点V$_{\rm PRV}$可以被检测,
按照本文故障链传播假定,初始事件"PRSO-V
卡在开位"的故障链即为终节点,无延续节点,标记为故障链①.
表示测试节点,
V表示阀门开度,F表示流量,P表示压力,T表示温度.
由于"PRSOV卡在开位"对应的状态节点V$_{\rm PRV}$可以被检测,
按照本文故障链传播假定,初始事件"PRSO-V
卡在开位"的故障链即为终节点,无延续节点,标记为故障链①.
对于初因事件"PRSOV调节压力偏大",其对应状态节点P$_{\rm PRV}$不是可监测节点,该故障可传播至后续节点P$_{\rm PIPS}$和T$_{\rm PEG}$,T$_{\rm PEG}$状态同样无法监测,故障继续传播, 直至可监测状态节点T$_{\rm BTS}$. 初始事件可能发生的延续事件包括"引气出口压力偏大"和"预冷器出口温度高", 记为故障链②.
初始事件"预冷器性能降低" 延续节点为T$_{\rm PEG}$, 故障可传播至T$_{\rm BTS}$. T$_{\rm PEG}$可能引发"预冷器出口温度高",记为故障链③.
以三个故障模式为起因事件的故障链见图 5.
 |
| 图 5 以三个故障模式为初始事件的故障链 |
2)其次,确定各事件风险指标值
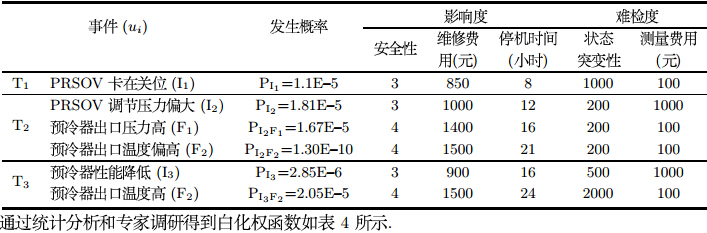
三个故障链中的初始事件并不复杂,其发生的概率通过统计即可得到. 然而故障链②和故障链③中初始事件的延续事件必须考虑事件发生的条件概率, 各事件发生概率如表 2所示.
为进一步计算这些事件发生的可能性,还需要分析导致该事件发生的原因. 以"引气出口压力高"为顶事件,(P$_{\rm PIPS} =+$)为瞬间样本值, 按照1.2节的方法,P$_{\rm PIPS}$为非控制节点, 其故障子树以相邻子节点通过"或"逻辑展开,如图 6所示. 以"引气出口温度高"为顶事件,(T$_{\rm BTS} =+$)为瞬间样本值, T$_{\rm BTS}$为负反馈回路节点,按照负反馈回路故障子树获取原因节点, 选择合适的操作符相连,最终得到故障子树如图 7所示.
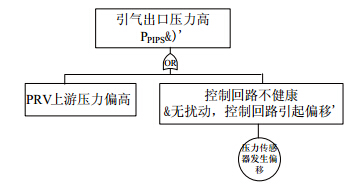 |
| 图 6 “引气出口压力低”故障子树 |
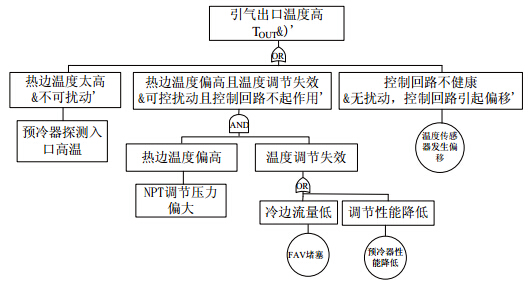 |
| 图 7 “引气出口温度高”故障子树 |
根据表 2相关的统计概率值、条件概率及图 6$\sim$7的故障树计算出各事件的发生概率: \[ \begin{array}{l} P({\rm I}_2{\rm F}_1) = P({\rm I}_2) \times P({\rm F}_1/{\rm I}_2),\\ P({\rm I}_2{\rm F}_2) = P({\rm I}_2) \times P({\rm F}_2)\times P({\rm F}_2/{\rm I}_2) \times(P({\rm A}) + P({\rm I}_3)),\\ P({\rm I}_3{\rm F}_2) = P({\rm I}_3) \times P({\rm F}_2/{\rm I}_3). \end{array} \] 式中,$P({\rm I}_2{\rm F}_1)$、 $P({\rm I}_2{\rm F}_2)$、 $P({\rm I}_3{\rm F}_2)$表示后果事件的发生概率. $P({\rm F}_1/{\rm I}_2)$、 $P({\rm F}_2/{\rm I}_2)$、$P({\rm F}_2/{\rm I}_3)$ 是条件概率.
通过统计分析和专家调研得到白化权函数如表 4所示.
得到一级指标权向量$w$、二级影响度标聚类权向量$w_2$和难检度聚类权向量$w_3$: \[ \begin{array}{l} w = [0.3~~0.5~~0.2],\\ w_2 = [0.45~~0.35~~0.2],\\ w_3 = [0.45~~0.55]. \end{array} \] 3)计算后果风险 由于篇幅限制,本文仅以故障链③为评估对象,计算初始事件及其后果风险. 故障链③评估样本矩阵为 \[ X_1 = \begin{bmatrix} 2.85{\rm E}-6 \\ 2.05{\rm E}-5 \\ \end{bmatrix},\qquad X_2 = \begin{bmatrix} 3 & 900 & 16 \\ 4 & 1400 & 24 \\ \end{bmatrix},\qquad X_3 = \begin{bmatrix} 500 & 1000 \\ 1000 & 100 \\ \end{bmatrix}. \]
两个故障的发生度、影响度和难测度向量矩阵分别为: \[ B_1 = \begin{bmatrix} b_{11} \\ b_{12} \\ \end{bmatrix} = \begin{bmatrix} w_1R_{11} \\ w_1R_{12} \\ \end{bmatrix} = \begin{bmatrix} (f_{11}(x_{111})) \\ (f_{11}(x_{121})) \\ \end{bmatrix} = \begin{bmatrix} 0.1 & 1.0 & 0.0 & 0.0 & 0.0 \\ 0.1 & 0.0 & 1.0 & 0.0 & 0.0 \\ \end{bmatrix}, \] \[ R_{21} = \begin{bmatrix} (f_{21}(x_{211})) \\ (f_{22}(x_{212})) \\ (f_{23}(x_{213})) \\ \end{bmatrix} = \begin{bmatrix} 0.0 & 0.0 & 1.0 & 0.0& 0.0 \\ 0.0 & 0.5 & 0.5 & 0.0& 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0& 0.0 \\ \end{bmatrix}, \] \[ R_{22} = \begin{bmatrix} (f_{21}(x_{221})) \\ (f_{22}(x_{222})) \\ (f_{23}(x_{223})) \\ \end{bmatrix} = \begin{bmatrix} 0.0 & 0.0 & 0.0 & 1.0& 0.0 \\ 0.0 & 0.5 & 0.5 & 0.5& 0.0 \\ 0.0 & 0.0 & 0.0 & 0.0& 1.0 \\ \end{bmatrix}, \] \[ b_2 = \begin{bmatrix} w_2R_{11} \\ w_2R_{22} \\ \end{bmatrix} = \begin{bmatrix} 0.0 & 0.175 & 0.625 & 0.2 & 0.0 \\ 0.0 & 0.0 & 0.175 & 0.625 & 0.2 \\ \end{bmatrix}, \] \[ R_{31} = \begin{bmatrix} (f_{31}(x_{311})) \\ (f_{32}(x_{312})) \\ \end{bmatrix} = \begin{bmatrix} 0.0 & 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.0 & 0.0 \\ \end{bmatrix}, \] \[ R_{32} = \begin{bmatrix} (f_{31}(x_{321})) \\ (f_{32}(x_{322})) \\ \end{bmatrix} = \begin{bmatrix} 0.0 & 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 1.0 & 0.0 & 0.0 & 0.0 \\ \end{bmatrix}, \] \[ b_3 = \begin{bmatrix} w_3R_{31} \\ w_3R_{32} \\ \end{bmatrix} = \begin{bmatrix} 0.0 & 0.0 & 0.45 & 0.55 & 0.0 \\ 0.0 & 0.55 & 0.0 & 0.45 & 0.0 \\ \end{bmatrix}. \]
故障链③中的两个事件的风险值为 \[ \begin{array}{l} \sigma_1 = w \begin{bmatrix} b_{11} \\ b_{21} \\ b_{31} \\ \end{bmatrix} = [0.3~~0.5~~0.2] \begin{bmatrix} 0.0 & 1.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 0.35 & 0.45 & 0.2 & 0.0 \\ 0.0 & 0.0 & 0.45 & 0.55 & 0.0 \\ \end{bmatrix} = [0.0~~0.475~~0.315~~0.21~~0.0], \\[5mm] \sigma_2 = w \begin{bmatrix} b_{12} \\ b_{22} \\ b_{32} \\ \end{bmatrix} = [0.3~~0.5~~0.2] \begin{bmatrix} 0.0 & 0.0 & 1.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.175 & 0.625 & 0.2 \\ 0.0 & 0.55 & 0.0 & 0.45 & 0.0 \\ \end{bmatrix} = [0.0~~0.11~~0.3875~~0.4025~~0.1]. \end{array} \]
由公式(7)得到各事件的综合风险值为: \[ \eta_1 = 2.735,\qquad \eta_2 = 3.4925. \]
对比故障模式取值范围表,可判断$\eta_2$为高风险,因此可得出本次评估故障链③属于高风险故障. 5 结论
本文针对已识别的故障模式, 根据SDG模型隔离故障链和生成故障树, 通过运用灰色聚类决策方法从定量的角度对故障风险进行辨识、 分析、量化、定级,为民机系统的安全性分析提供决策依据. 相比其他故障风险评估方法,该方法可以体现故障模式的发展变化过程,更 全面反映故障的发展特点及其对系统造成的危害, 使故障风险评估更具系统性和客观性. 所得结果不仅是故障模式的风险优先顺序,还包 括更具实用意义的中间过程详细分析结果, 为进一步开展根据不同故障的风险等级和其故障的特性合理地给出相应的辅助维修决策研究提 供建议.
| [1] | 康锐, 石荣德. FMECA技术及其应用[M].北京: 国防工业出版社, 2006. Kang Rui, Shi Rongde. FMECA technology and its application[M]. Beijing: National Defence Industry Press, 2006. |
| [2] | 曾声奎, 赵廷弟, 张建国, 等.系统可靠性设计分析教程[M].北京: 北京航空航天大学出版社, 2001.Zeng Shengkui, Zhao Tingdi, Zhang Jianguo, et al. Tutorial of system reliability design and analysis[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2001. |
| [3] | Bowlesj B. An assessment of RPN prioritization in a failure modes effects and criticality analysis[C]// Proceedings of the Annual Reliability and Maintainability Symposium, 2003: 380-385. |
| [4] | Pillay A, Wang J. Modified failure mode and effects analysis using approximate reasoning[J]. Reliability Ensinecfing and System Safety, 2003, 79: 69-85. |
| [5] | 戴荣, 康锐. RCM决断流程与风险评估[J].航空工程与维修, 2001(6): 10-11. Dai Rong, Kang Rui. The RCM process and risk assessment[J]. Aviation Engineering and Maintenance, 2001(6): 10-11. |
| [6] | 王品刚, 卓华.基于风险评估的设备维修方法的研究与应用[J].电力信息化, 2004, 2(11): 87-88.Wang Pingang, Zhuo Hua. Research and application of method for equipment maintenance based on risk assessment[J]. Electric Power Information, 2004, 2(11): 87-88. |
| [7] | 董玉亮, 顾煜炯, 杨昆.基于灰色理论和RCM分析的发电设备风险分析[J].动力工程, 2004, 24(6): 798-800.Dong Yuliang, Gu Yujiong, Yang Kun. Risk analysis of power plant equipment based on grey theory and RCM analysis[J]. Power Engineering, 2004, 24(6): 798-800. |
| [8] | Kokawa M, Shingai S. Failure propagating simulation and nonfailure paths search in network systems[J]. Automatica, 1982, 18(3): 335-341. |
| [9] | Kokawa M, Miyazaki S, Shingai S, et al. Safety analysis of boil off gas treatment system using failure propagation simulator[C]// Annual Conference Records of SICE of Japan, 1983: 361-362. |
| [10] | Iri M, Aoki K, O'shima E, et al. An algorithm for diagnosis of system failures in the chemical process[J]. Computer & Chemical Engineering, 1979, 3(1): 489-493. |
| [11] | Iri M, Aoki M, O'shima E, et al. A graphical approach to the problem of locating the origin of the system failure[J]. Journal of the Operations Research Society of Japan, 1980, 23(4): 295-311. |
| [12] | 杨帆, 萧德云. SDG建模及其应用的进展[J].控制理论与应用, 2005(5): 767-774. Yang Fan, Xiao Deyun. Review of SDG modeling and its application[J]. Control Theory & Applications, 2005(5): 767-774. |
| [13] | 周虹, 左洪福, 蔡景, 等.基于TMSDG的民用飞机故障诊断隔离策略研究[J].航空学报, 2012, 32(3): 479-486. Zhou Hong, Zuo Hongfu, Cai Jing, et al. Research on fault diagnosis and isolation strategy for civil aircraft based on TMSDG[J]. Acta Aeronautica et Astronautica Sinica, 2012, 32(3): 479-486. |
| [14] | 宋其江, 徐敏强, 王日新. 基于分层有向图的航天器故障诊断[J].航空学报, 2009, 30(6): 1058-1062. Song Qijiang, Xu Minqiang, Wang Rixin. Spacecraft fault diagnosis based on hierarchical digraphs[J] . Acta Aeronautica et Astronautica Sinica, 2009, 30(6): 1058-1062. |
| [15] | 邓聚龙.灰理论基础[M].武汉: 华中科技大学出版社, 2002.Deng Julong. Grey theory[M]. Wuhan: Huazhong University of Science and Technology Press, 2002. |
| [16] | 施国洪, 姚冠新.灰色系统理论在故障诊断决策中的应用[J].系统工程理论与实践, 2001, 21(4): 120-123.Shi Guohong, Yao Guanxin. Application of grey system theory in fault tree diagnosis decision[J]. Systems Engineering——Theory & Practice, 2001, 21(4): 120-123. |
| [17] | 余锋杰, 柯映林, 应征.飞机自动化对接装配系统的故障维修决策[J].计算机集成制造系统, 2009, 15(9): 1823-1830.Yu Fengjie, Ke Yinglin, Ying Zheng. Decision on failure maintenance for aircraft automatic join-assembly system[J]. Computer Integrated Manufacturing Systems, 2009, 15(9): 1823-1830. |