0 引言
无论是在民用或是军事领域,在保证设备正常运转方面, 备件维修供应系统起着重要的作用. 当系统中设备数量较大时, 可以假定故障件的到达服从泊松分布; 当维修机构利用率很低时, 可以假定维修渠道无限大. 基于这两个假设可以方便地使用帕尔姆定理, 易于处理,Sherbrooke以此为基本假设, 建立了著名的METRIC模型[1]. METRIC模型计算方便, 在一定条件下精度很高,故而得到广泛的应用[2, 3, 4, 5].
无限维修渠道的假设便于系统分析,但在维修机构利用率较高时, 会引起较大的误差. Diaz等[6]使用M/M/c模型和M/G/c模型对有限维修渠道两级库存系统进行了分析, 研究结果表明在维修机构利用率较高时$(> 0.6)$, Diaz的模型比经典的METRIC模型有更精确的结果. Kim等[7, 8]研究了由若干基层站点和一个后方站点构成的单类设备两级维修供应系统, 各站点的维修渠道有限,采用M/M/c模型分析各级站点维修队列. Jung等[9]研究了两级维修供应系统,基层库存之间可以横向供应, 基地站点不设库存,使用M/M/c模型描述各级站点的维修队列. Kim等[10]在文献[7, 8]的基础上放宽了对故障件维修时间概率分布的假设, 采用M/G/c模型分析了各站点的维修队列, 但该模型中依旧只包含一类故障件. Rappold等[11]在有限维修渠道条件下建立了单类备件库存的整数规划模型. Mirzahosseinian等[12]研究了基于性能的后勤保障策略, 为库存系统建立了有限顾客源的M/M/c排队模型. Park等[13]研究了带有零部件库存的两级维修供应系统, 将整个网络进行分解简化,并对子网建立了多类可修设备的BCMP 闭环排队网络模型. 在国内方面, 有限维修渠道条件下的多级维修供应模型较为少见, 张建军等[14]基于BCMP闭环排队网络建立了作战单元多级维修供应模型, 系统中有多类可修部件,各级站点的维修渠道可以根据实际设定. 阮#[29]智等[15]采用M/M/c模型分析各级维修队列, 对故障件的平均维修时间及备件供应渠道进行了修正, 根据保障点总备件需求量的差均比选择合适的分布来描述备件需求量的稳态分布.
本文在有限维修渠道条件下研究了两级维修供应系统, 对Kim模型[7, 8]中的系统性能评估部分进行了扩展, 建立了多类故障件条件下的维修供应能力评估模型. 第1节介绍了两级维修供应系统,并给出建模的基本假设. 第2节在给定的资源配置下,采用M/M/c模型分析各级站点维修队列; 对于运输队列,采用M/G/$\infty$模型进行分析, 求得各级站点备件申请量的稳态分布,从而计算备件缺货量、备件满足率, 用以评估系统的维修供应能力. 第3节举例介绍模型的使用, 给出了相同假设条件下的仿真结果、METRIC结果和本文模型结果, 通过结果对比来验证本文模型的有效性. 1 问题描述与基本假设
假定某区域有一个两级维修供应系统,如图 1所示, 负责供应该区域内的备件申请和故障件的维修,故障件有多种类别. 系统由若干基层维修保障点,一个基地维修保障点构成, 每个站点又分为备件库存和维修机构两部分. 在每个站点, 各类故障件均有对应的备件库存,各类故障件共用同一套维修机构, 维修渠道有限.每个基层站点负责一个子区域内故障件的维修和备件供应. 故障件到达基层站点后,如果该站点的库存有备件,则将该备件替换故障件,完成一次备件供应; 如果没有备件,该站点库存发生一次备件短缺. 基层站点的维修机构能修复一部分故障件,其余故障件送往基地站点, 同时向基地库存申请一个备件. 基层站点每获得一个完好备件(本级维修机构修复, 或从基地库存获得补充),则本站点库存增加一件备件或减少一件缺货. 基层库存减少一件缺货,意味着完成一次备件供应, 只是该次供应有后勤延误. 基层站点和基地站点之间有一定的距离, 运送故障件花费一定的时间. 基地站点的维修与供应与基层站点基本相同, 但基地维修机构能修复所有故障件; 对于任意故障件, 基地站点会记录是从哪个基层站点得到的.
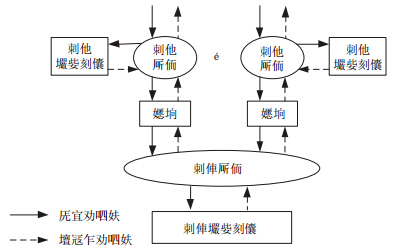 |
| 图 1 两级维修供应系统 |
本文模型包含如下几个基本的建模假设:
1)顾客源无限大,一定时间内,各类故障件的到达率服从泊松分布;
2)所有站点的库存施行连续检查的($S-1,S$)策略, 缺少一件立即送至本级维修机构;
3)故障件到达基层站点后立即检测是否能在基层站点修复, 检测时间忽略不计,不考虑各基层库存之间的横向供应;
4)各类故障件不分优先级, 在各场站按先到先服务、先申请先补充的规则进行维修和供应;
5)各级站点维修时间服从负指数分布,运输时间服从一般分布. 2 系统性能评估模型
本节在给定的维修资源和备件资源配置下, 计算备件满足率、平均缺货量等性能指标, 评估系统的备件维修及供应能力. 备件申请量的稳态分布是求解备件满足率、平均缺货量的关键. 无限维修渠道假设的METRIC模型采用M/G/$\infty$模型描述故障件的维修供应队列, 备件申请量服从泊松分布. 本文避免了无限维修渠道的假设, 采用M/M/c模型描述故障件在各级站点的维修队列, 采用M/G/$\infty$模型描述往返于基地站点和基层站点之间的运输队列, 并计算得到各个环节的稳态分布. 基地站点的备件申请量可以根据其维修队列的稳态分布直接得到. 基层站点的备件申请量分散于本站点维修队列、运输队列和基地站点维修队列中, 本文在各个环节稳态分布基础上, 采用卷积法计算各基层站点备件申请量的稳态分布.
在Kim[7, 8]的模型中,系统接受的故障件只有1类, 所以维修队列和运输队列可看作单类顾客排队系统, 可直接用M/M/c排队模型进行分析, 很容易计算顾客在各级站点维修队列和运输队列中的稳态分布. 如果假定有多类故障件,将大大增加顾客稳态分布的计算难度, 本文正是在这一方面进行研究,假定有多类故障件, 扩展了Kim[7, 8]的模型. 2.1 基层维修队列稳态分布
假定系统有$I$个基层站点,各基层站点接受的故障件有$J$类. 令$\lambda_{ij}$、$\mu_{ij}$分别表示第$i$个基层站点中第$j$类故障件到达速度和维修率 ($i=1,2,\cdots,I$; $j=1,2,\cdots,J$),各类故障件共用一套维修设备, $c_i$表示基层站点$i$的维修渠道数.
由于包含多类故障件, 各基层站点的维修机构可以看作一个多类顾客多服务台M/M/c排队系统, 基地站点维修机构也是如此. 为了便于分析, 将多类顾客多服务台M/M/c排队系统转化为单类顾客多服务台M/M/c排队系统[15, 16].
令$\alpha_{ij}$表示第$j$类故障件能在站点$i$得到修复的概率, 则进入各基层维修机构的故障件到达率为
| \begin{eqnarray} \lambda_B^i=\sum_{j=1}^J{\alpha_{ij}\lambda_{ij}} \end{eqnarray} | (1) |
令$\rho_{ij}$表示第$j$类故障件对基层站点$i$维修机构的占用率(即利用率), 总的利用率$\rho_{i}$为
| \begin{eqnarray} \rho_i=\sum_{j=1}^J{\rho_{ij}}=\frac{1}{c_i}\sum_{j=1}^J{\frac{\alpha_{ij}\lambda_{ij}}{\mu_{ij}}} \end{eqnarray} | (2) |
令$\mu_i$表示基层站点$i$维修机构的平均维修速度, 根据维修机构利用率的定义可得
| \begin{eqnarray} \mu_i=\frac{\lambda_B^i}{c_i\rho_i}=\frac{\lambda_B^i}{\sum_{j=1}^J{\frac{\alpha_{ij}\lambda_{ij}}{\mu_{ij}}}}= \bigg[\sum_{j=1}^J{\frac{\theta_{ij}}{\mu_{ij}}}\bigg]^{-1} \end{eqnarray} | (3) |
根据式(1)$\thicksim$(3), 可用单类顾客多服务台M/M/c模型描述各基层站点的维修队列, 故障件到达率为$\theta_{ij}\lambda_B^i$,维修率为$\mu_i$, 维修渠道利用率为$\rho_i$,且维修渠道仍为$c_i$. 令$X_B^i$表示稳态时基地站点维修队列中故障件的数量, $P(X_B^i=N)$表示各基地级维修队列中故障件数目为$N$的概率, 稳态分布为
| \begin{eqnarray} P(X_B^i=0)=\bigg[\sum_{l=0}^{c_i-1}{\frac{(c_i\rho_i)^l}{l!}}+\frac{(c_i\rho_i)^{c_i}}{c_i!(1-\rho_i)}\bigg]^{-1} \end{eqnarray} | (4) |
| \begin{eqnarray} P(X_B^i=n)= \begin{cases} \frac{(c_i\rho_i)^n}{n!}P(X_B^i=0),& n=1,2,\cdots,c_i\\ \frac{(c_i\rho_i)^n}{c_i!c_i^{n-c_i}}P(X_B^i=0),& n>c_i \end{cases} \end{eqnarray} | (5) |
令$X_B^{ij}$表示各基层站点维修队列中第$j$类故障件的数量. 在基层站点$i$维修机构的等待队列中, 第$j$类故障件所占的比例取决于故障件的到达速度,为$\theta_{ij}$; 稳定状态下,故障件的离去速度等于故障件的到达速度, 正在接受服务的故障件中,第$j$类故障件的平均队长为$c_i \rho_{ij}$, 所有故障件的总队长为$c_i\rho_i$, 所以在第$j$类故障件的所占的比例为$\gamma_{ij}=\rho_{ij}/\rho_i$.
当$X_B^i=N\leq c_i$时,所有故障件都在接受维修, $N$个故障件中有$n$个第$j$故障件的概率可以表示为:
| \begin{eqnarray} P(X_B^{ij}=n|X_B^i=N\leq c_i)={N \choose n}(\gamma_{ij})^n(1-\gamma_{ij})^{N-n}P(X_B^i=N) \end{eqnarray} | (6) |
当$X_B^i=N>c_i$时,正在接受维修的故障件数量为$c_i$, 正在排队等待维修的故障件数量为$N-c_i$, 于是$N$个故障件中有$n$个第$j$故障件的概率可以表示为:
| \begin{eqnarray}\begin{split} P(X_B^{ij}=n|X_B^i=N>c_i)= & \sum_{n_s+n_w=n}{{c_i \choose n_s}(\gamma_{ij})^{n_s}(1-\gamma_{ij})^{c_i-n_s}\times}\\ & {N-c_i \choose n_w}(\theta_{ij})^{n_w}(1-\theta_{ij})^{N-c_i-n_w}P(X_B^i=N) \end{split}\end{eqnarray} | (7) |
结合式(6)和式(7), 基层站点$i$的维修队列中有$n$个第$j$类故障件的概率为:
| \begin{equation}\begin{split} P(X_B^{ij}=n)=& \sum_{N=0}^{c_i}{{N \choose n}}(\gamma_{ij})^n(1-\gamma_{ij})^{N-n}P(X_B^i=N)+\\ & \sum_{N=c_i+1}^\infty {\sum_{n_s+n_w=n}{{c_i \choose n_s}(\gamma_{ij})^{n_s}\\(1-\gamma_{ij})^{c_i-n_s}{N-c_i \choose n_w}(\theta_{ij})^{n_w}(1-\theta_{ij})^{N-c_i-n_w}P(X_B^i=N)}} \end{split}\end{equation} | (8) |
如果各类部件的维修率相等,则有$\gamma_{ij}=\theta_{ij}$,于是
| \begin{eqnarray}\begin{split} P(X_B^{ij}=n)=&\sum_{N=0}^{c_i}{{N \choose n}}(\theta_{ij})^n(1-\theta_{ij})^{N-n}P(X_B^i=N)+\\ &\sum_{N=c_i+1}^\infty {\sum_{n_s+n_w=n}{{c_i \choose n_s}(\theta_{ij})^{n_s}(1-\theta_{ij})^{c_i-n_s}\\{N-c_i \choose n_w}(\theta_{ij})^{n_w}(1-\theta_{ij})^{N-c_i-n_w}P(X_B^i=N)}}\\ =&\sum_{N=0}^{c_i}{{N \choose n}}(\theta_{ij})^n(1-\theta_{ij})^{N-n}P(X_B^i=N)+\\ \sum_{N=c_i+1}^{\infty}{{N \choose n}}(\theta_{ij})^n(1-\theta_{ij})^{N-n}P(X_B^i=N)\\ =&\sum_{N=0}^{\infty}{{N \choose n}}(\theta_{ij})^n(1-\theta_{ij})^{N-n}P(X_B^i=N)\\ \end{split}\end{eqnarray} | (9) |
不能在基层站点修复的故障件立即进入运输队列,送往基地站点; 基地站点接申请后,库存中如有备件立即送往相应基层站点, 虽然送往基层站点的备件都是完好的,但由于尚未交付使用, 故而在计算基层站点的备件申请量时也要考虑在内. 令$X_t^{ij}$表示往返于基地站点和第$i$个基层站点之间的第$j$类设备数量, 各类故障件的运输时间都为$T_t^i$,使用M/G/$\infty$模型描述运输队列, 根据帕尔姆定理,$X_t^{ij}$服从泊松分布:
| \begin{eqnarray} P(X_t^{ij}=m)=\frac{[(1-\alpha_{ij})\lambda_{ij}T_t^i]^m\exp[-(1-\alpha_{ij})\lambda_{ij}T_t^i]}{m!} \end{eqnarray} | (10) |
基地维修队列建模方法同基层维修队列. 令$c_D$表示基地站点维修渠道数, $\mu_D^j$表示对第$j$类故障件的维修率,在基地站点, 第$j$类故障件的到达率和$J$类故障件的总到达率分别为
| \begin{eqnarray} \lambda_D^j=\sum_{i=1}^I{(1-\alpha_ij)\lambda_{ij}} \end{eqnarray} | (11) |
| \begin{eqnarray} \Lambda=\sum_{j=1}^J{\lambda_D^j}=\sum_{j=1}^J{\sum_{i=1}^I{(1-\alpha_{ij})\lambda_{ij}}} \end{eqnarray} | (12) |
基地站点维修机构的平均维修速度为
| \begin{eqnarray} \mu_D=\bigg[\sum_{j=1}^J\frac{\theta_D^j}{\mu_D^j}\bigg]^{-1} \end{eqnarray} | (13) |
令$X_D$表示稳态时基地站点维修队列中$J$类故障件的总数, $P(X_D=N)$表示基地维修队列中故障件数目为$N$的概率,则稳态分布为
| \begin{eqnarray} P(X_D=0)=\bigg[\sum_{l=0}^{c_D-1}{\frac{(c_D\rho_D)^l}{l!}}+\frac{(c_D\rho_D)^{c_D}}{c_D!(1-\rho_D)}\bigg]^{-1} \end{eqnarray} | (14) |
| \begin{eqnarray} P(X_D=N)= \begin{cases} \frac{(c_D\rho_D)^N}{N!}P(X_D=0),& N=1,2,\cdots,c_D\\ \frac{(c_D\rho_D)^N}{c_D!c_D^{N-c_D}}P(X_D=0),& N>c_D \end{cases} \end{eqnarray} | (15) |
在基地维修机构的等待队列中, 第$j$类故障件所占的比例取决于故障件的到达速度,为$\theta_D^j$; 正在接受服务的故障件中, 第$j$类故障件的所占的比例为$\gamma_D^j=\rho_D^j/\rho_D$. 基地站点维修队列中有$K$个第$j$类故障件的概率为:
| \begin{eqnarray}\begin{split} P(X_D^{j}=K)=&\sum_{N=0}^{c_D}{{N \choose K}}(\gamma_{D}^j)^K(1-\gamma_{D}^j)^{N-k}P(X_D=N)+\\ &\hspace{-6mm}\sum_{N=c_D+1}^\infty {\sum_{K_s+K_w=K}{{c_D \choose K_s}(\gamma_{D}^j)^{K_s}(1\!-\!\gamma_{D})^{c_D-K_s} {N\!-\!c_D \choose K_w}\\(\theta_{D})^{K_w}(1\!-\!\theta_{D}^j)^{N\!-\!c_D\!-\!K_w}P(X_D\!=\!N)}} \end{split}\end{eqnarray} | (16) |
本文考虑了各类设备在基地站点的备件库存, 令$s_D^j$表示基地库存中第$j$类设备的备件存储量. Kim[7]的模型没有考虑基地库存,且只有1类设备; 在Kim[8]的模型中,考虑了基地库存,但依旧只有1类设备. 基地库存对第$j$类故障件的备件满足率$f_D^j$和平均缺货数$EBO_D^j$分别为
| \begin{eqnarray} f_D^j=\sum_{K=0}^{s_D^j-1}{P(X_D^j)=K} \end{eqnarray} | (17) |
| \begin{eqnarray} EBO_D^j=\sum_{K=s_D^j}^\infty{(K-s_D^j)P(X_D^j=K)} \end{eqnarray} | (18) |
计算各基层站点备件满足率和平均缺货数时, 需要先得到各基层站点备件申请量的稳态分布. 前面已经指出基层站点的备件申请量分散于本站点维修队列、运输队列和基地站点维修队列中.
令$X_D^{ij}$表示基地维修队列的第$j$类故障件中, 来自第$i$个基层站点的数量,稳定状态下, 当基地站点的第$j$类故障件总数为$K$时,其中$k(0\leq k\leq K)$个来自第$i$个基层站点的概率为
| \begin{eqnarray} P(X_D^{ij}=k|X_D^j=K)={K \choose k}(\theta_D^{ij})^k(1-\theta_D^{ij})^{K-k} \end{eqnarray} | (19) |
| \begin{eqnarray} P(X_D^{ij}=k)=\sum_{K=0}^\infty{{K \choose k}(\theta_D^{ij})^k(1-\theta_D^{ij})^{K-k}}P(X_D^j=K) \end{eqnarray} | (20) |
从式(17)可知,当$s_D^j=0$时,基地站点的备件满足率$f_D^j=0$, 计算基层站点备件申请量时, 基地站点维修队列中的任一故障件均须考虑进去, 故而基层站点备件申请量的稳态分布为$X_B^{ij}$、$X_t^{ij}$与$X_D^{ij}$三个随机变量稳态分布的卷积. 但是当$s_D^j>0$时,有$f_D^j>0$,基层不能修复的故障件到达后, 不能立即得到补充的概率为$(1-f_D^j)$, 计算基层站点备件申请量在基地站点的分布时, 只需考虑在基地站点不能立即得到补充的部分,记为$Y_D^{ij}$, 基层站点的备件申请量的稳态分布为$X_B^{ij}$、$X_t^{ij}$与$Y_D^{ij}$的卷积.
当基地维修队列中第$j$类故障件总数$X_D^j=K<s_D^j$时, 来自基层站点的所有备件申请都已得到补充, 故有$P(Y_D^{ij}=0|X_D^j=K<s_D^j)=1$,$P(Y_D^{ij}\neq 0|X_D^j=K<s_D^j)=0$; 当$X_D^j=K\geq s_D^j$时, 有$K-s_D^j$个故障件还没有得到替换, 需要计算$K-s_D^j$个故障件中来自第$i$个基层站点的数量. 根据分析可知$Y_D^{ij}=k$的概率为 \begin{eqnarray}\begin{split} P(Y_D^{ij}=k)= & \begin{cases} \sum_{N=0}^{s_D^j-1}{P(X_D^j=K)}+\sum_{N=s_D^j}^{\infty}{{K-s_D^j \choose k}(\theta_D^{ij})^k(1- \theta_D^{ij})^{K-s_D^j-k}P(X_D^j=K)},& k=0\\ \sum_{N=s_D^j}^{\infty}{{K-s_D^j \choose k}(\theta_D^{ij})^k(1-\theta_D^{ij})^{K-s_D^j-k}P(X_D^j=K)},& k>0 \end{cases}\\ =& {0 \choose k}P(X_D^j\leq s_D^j-1)+\sum_{K=s_D^j}^{\infty}{K-s_D^j \choose k}(\theta_D^{ij})^k(1-\theta_D^{ij})^{K-s_D^j-k}P(X_D^j=K) \end{split}\end{eqnarray}
令$X_{ij}$表示基层站点$i$第$j$类设备的备件申请量, 其稳态分布为$X_B^{ij}$、$X_t^{ij}$与$Y_D^{ij}$稳态分布的卷积, 可以表示为
| \begin{eqnarray} P(X_{ij}\!=\!Z)\!=\! \!\sum_{n+m+k}\!\!\!{P(X_B^{ij}\!=\!n)P(X_t^{ij}\!=\!m)P(Y_B^{ij}\!=\!k)} \!=\! \\\sum_{n=0}^Z{\sum_{m=0}^{Z-n}\!P(X_B^{ij}\!=\!n)P(X_t^{ij}\!=\!m)P(Y_B^{ij}\!=\!Z\!-\!n\!-\!m)} \end{eqnarray} | (22) |
\qquad 令$s_{ij}$表示基层站点$i$的库存中第$j$类设备的备件存数量, 基层站点$i$对第$j$类设备的备件满足率$f_B^{ij}$和平均缺货量$EBO_B^{ij}$分别为
| \begin{eqnarray} f_B^{ij}=\sum_{Z=0}^{s_{ij}-1}P(X_{ij}=Z) \end{eqnarray} | (23) |
| \begin{eqnarray} EBO_B^{ij}=\sum_{Z=s_{ij}}^\infty{(Z-s_{ij})P(X_{ij}=Z}) \end{eqnarray} | (24) |
本节举例介绍模型的应用, 在给定的各类故障件到达率、资源配置、维修能力等条件下, 计算各级站点的备件满足率和平均缺货量. 对于图 1所示两级维修供应系统, 假设有2个基层站点$M_1$和$M_2$,1个基地站点$M_D$,故障件共有2类, $S_1$和$S_2$,各级站点的相关参数如表 1所示, 表中与时间相关的量没有指明时间的单位,但不妨碍进行分析. 故障件从$M_1$到$M_D$的往返运输时间为10个单位; 从$M_2$到$M_D$的往返时间为8个单位.
在想定的情景下, 使用第3节评估模型计算了各级站点的备件满足率和平均缺货量, 如表 2所示. 为了验证本文模型的有效性,在相同的情景想定下, 采用离散事件仿真方法对图 1所示两级维修供应系统进行仿真分析, 得到了各级站点备件满足率和平均缺货量的统计结果,如表 2所示. 表 2还给出了本文模型结果相对于仿真结果的误差.
在想定情景下,$M_D$、$M_1$和$M_2$等站点的资源利用率分别为0.80, 0.79,0.73. 前面已经指出,在实际的维修渠道利用率较高时, 无限维修渠道假设的METRIC模型会产生较大的误差. 本文模型避免了无限维修渠道的假设, 为了验证本文评估模型相对于METRIC模型的优势,在相同情景想定下, 采用METRIC模型计算了系统的备件满足率和平均缺货量, METRIC结果及其相对于仿真结果的误差如表 2所示.
从表 2可知,本文模型与仿真结果的误差较小, 备件满足率的最大误差为1.56\%,大部分都在1\%以内; 平均缺货量的最大误差为$-3.27\%$,其它都在3\%以内. 无限维修渠道假设的METRIC计算结果与仿真结果的误差很大, 原因在于维修渠道利用率较高,故障件到达后有一定的等待时间, 而METRIC模型忽略了等待时间.
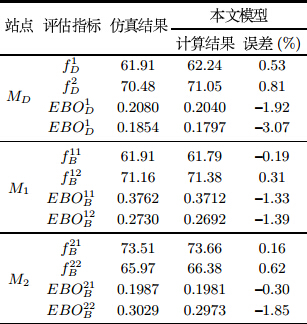
在维修渠道充足(其它参数同表 1)条件下, 本文模型和仿真方法的结果对比如表 3所示,结果对比显示, 本文模型结果与仿真结果的误差最大为$-3.07\%$,其余都在2\%以内. 在维修渠道充足条件下,故障件进入维修机构后不需等待, 能立即得到维修,与METRIC模型的假设一致. 不论实际的维修渠道是否充足,METRIC模型均按维修渠道无限来计算, 所以在维修渠道充足(其它参数同表 1)条件下的METRIC结果即为表 2中METRIC结果. 结合表 2、表 3可知,在维修渠道充足时, METRIC模型计算结果与仿真结果误差很小, 与本文模型的计算结果基本吻合. 表 2和表 3中计算结果的对比验证了本文模型的有效性, 以及在维修渠道利用率较高时相对于METRIC模型的优势.
本文基于排队理论研究了两级维修供应系统, 改进了Kim[7, 8]的评估方法, 从系统中只有单类故障件扩展到有多类故障件, 以备件满足率和平均缺货量为评估指标, 建立了两级维修供应系统性能评估模型, 适用于评价顾客源规模较大的备件维修供应系统. 与METRIC模型相比, 本模型避免了无限维修渠道的假设,使模型有更强的适应性. 使用M/M/c模型分析各级站点的维修队列,在维修渠道充足时, 本文模型与METRIC模型结果一致,与仿真结果的误差也很小;维修渠道有限, 且维修渠道利用率较高时(本文算例中三个站点的维修渠道利用率均在0.8左右), METRIC模型结果与仿真结果的误差很大, 而本文模型结果与仿真结果误差很小. 相同条件下的结果对比验证了本文模型的有效性, 以及在维修渠道利用率较高时相对于METRIC模型的优势.
本文两级维修供应系统性能评估模型是一个通用模型, 可用于民用、军用保障系统备件供应能力的评估. 对于库存优化问题, 本文没有进行研究,但是在本文评估模型基础上, 可以使用边际分析等常用算法很方便地对库存进行优化.
| [1] | Sherbrooke C C. METRIC: A multi-echelon technique for recoverable item control[J]. Operations Research, 1968, 16(1): 122-141. |
| [2] | Patten M P. Forecasting carrier air-wing operational availability with event step simulation[D]. Monterey: Naval Postgraduate School, 1999: 9-23. |
| [3] | 付兴方, 李继军, 李宗值.基于两级供应关系的可修复航材存储策略模型研究[J].系统工程理论与实践, 2004, 24(1): 111-115.Fu Xingfang, Li Jijun, Li Zongzhi. A stock strategy model for restoring air materiel based on the two-level providing condition[J]. Systems Engineering——Theory & Practice, 2004, 24(1): 111-115. |
| [4] | Sun L, Zou H F. Multi-echelon inventory optimal model of civil aircraft spare parts[C]// Proceedings of 2010 Chinese Control and Decision Conference, Xuzhou, China, 2010: 824-828. |
| [5] | 聂涛, 盛文, 王晗中.装备备件两级闭环供应链库存优化与分析[J].系统工程理论与实践, 2010, 30(12): 2309-2314. Nie Tao, Sheng Wen, Wang Hanzhong. Optimizing and analyzing tow-echelon closed loop supply chain storage system for equipment spare parts[J]. Systems Engineering——Theory & Practice, 2010, 30(12): 2309-2314. |
| [6] | Diaz A, Fu M C. Models for multi-repairable item inventory systems with limited repair capacity[J]. European Journal of Operational Research, 1997, 97(3): 480-492. |
| [7] | Kim J S, Shin K C, Yu H K. Optimal algorithm to determine the spare inventory level for a repairable-item inventory system[J]. Computers & Operations Research, 1996, 23(3): 289-297. |
| [8] | Kim J S, Shin K C, Park S K. An optimal algorithm for repairable-item inventory systems with depot spares[J]. Journal of the Operational Research Society, 2000, 51(3): 350-357. |
| [9] | Jung B R, Sun B G, Kim J S, et al. Modeling lateral transshipments in multi-echelon repairable item inventory systems with finite repair channels[J]. Computers & Operations Research, 2003, 30(9): 1401-1417. |
| [10] | Kim J S, Kim T Y, Hur S. An algorithm for repairable item inventory system with depot spares and general repair time distribution[J]. Applied Mathematical Modeling, 2007, 31(5): 795-804. |
| [11] | Rappold J A, Van Roo B D. Designing multi-echelon service parts networks with finite repair capacity[J]. European Journal of Operational Research, 2009, 199(3): 781-792. |
| [12] | Mirzahosseinian H, Piplani R. A study of repairable parts inventory system operating under performance-based contract[J]. European Journal of Operational Research, 2011, 214(2): 256-261. |
| [13] | Park C W, Lee H S. A multi-class closed queueing maintenance network model with a parts inventory system[J]. Computers & Operations Research, 2011, 38(11): 1584-1595. |
| [14] | 张建军, 刘芳, 张涛, 等.基于BCMP排队网络的作战单元备件保障度评估模型[J].兵工学报, 2009, 30(1): 110-113.Zhang Jianjun, Liu Fang, Zhang Tao, et al. The model of combat unit spares availability based on BCMP queueing network[J]. Acta Armamentarii, 2009, 30(1): 110-113. |
| [15] | 阮旻智, 李庆民, 黄傲林, 等.有限维修渠道约束下多级维修供应系统库存控制[J].航空学报, 2012, 33(11): 2018-2027.Ruan Minzhi, Li Qingmin, Huang Aolin, et al. Inventory control of multi-echelon maintenance supply system under finite repair channel constraint[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2018-2027. |
| [16] | Sleptchenko A, van Heijden M C, van Harten A. Effects of finite repair capacity in multi-echelon multi-indenture service part supply systems[J]. International Journal of Production Economics, 2002, 79(3): 209-230. |