2. 海军航空工程学院 基础实验部, 烟台 264001;
3. 海军装备部 军械保障部, 北京 100841
2. Basic Experiment Department, Naval Aeronautical Engineering Academy, Yantai 264001, China;
3. Ordnance Support Department of Naval Equipment Ministry, Beijing 100841, China
0 引言
战备完好性是指装备在接到作战训练命令时响应作战训练任务的能力[1]. 它是部队装备在编实力、装备可用性、训练等因素综合作用的结果, 是系统综合保障的总体指标,也是衡量导弹系统战斗力的重要指标之一. 战备完好率是战备完好性的概率度量,表示当要求装备投入作战训练时, 装备准备好能够执行任务的概率[2]. 导弹战备完好率是导弹保障部队常用的描述导弹装备可用状态的统计量, 是衡量导弹战备完好性的重要数值指标之一. 文献[3, 4, 5]对装备的战备完好性进行了有意义的研究, 但这些研究都是基于装备的概率模型和统计模型, 数据来源多为时间概率的统计值,对部队保障工作指导意义不强. 据此, 笔者结合现役导弹部队实际保障情况,开展导弹战备完好率评估模型研究, 结合导弹服役的相关数据,对导弹装备战备完好率进行评估验证, 对于实现导弹战备完好性评估与维修保障资源优化配置具有重要意义. 1 战备完好率参数
装备类型、任务范围和使用特点的不同, 决定了其战备完好性参数也不同. 常用的战备完好性参数有战备完好率、 使用可用度、能执行任务率、出动架次等. 根据导弹装备的特点, 战备完好率是度量其战备完好性的重要参数之一. 战备完好率 是针对下一次任务而言,即下次要求系统使用时,系统可用的概率. 当装备在上次任务中没有发生需修理 的故障, 则装备立即投入下次任务使用; 当装备在上次任务中发生需修理的故障, 但在下次任务来临之前可以修好,装备仍可投入下次任务使用. 这种情况下,战备完好率可表示为:
| \begin{equation}\label{1} P_{OR}=R(t)+Q(t)\times P(t_{m}<t_d) \end{equation} | (1) |
设故障修理时间概率密度函数为$f(t_m)$, 下一任务到达时间概率密度函数为$g(t_d)$,维修从上次任务结束开始, 则故障修理时间比下一任务到达时间短的概率为:
| \begin{equation}\label{2} P({t_m} < {t_d}) = \int_0^\infty {f({t_m})\left[ {\int_{{t_m}}^\infty {g({t_d})} } \right]} {\rm d}{t_m} \end{equation} | (2) |
如果故障修理时间和下一任务到达时间都服从指数分布, 故障平均修复时间为${M_1}$,下一任务到达平均时间为$M_2$,则:
| \begin{equation}\label{3} P({t_m} < {t_d}) = \frac{{{M_2}}}{{{M_1} + M{}_2}} \end{equation} | (3) |
从而可得:
| \begin{equation}\label{4} {P_{OR}} = R(t) + Q(t) \cdot \frac{{{M_2}}}{{{M_1} + M{}_2}} \end{equation} | (4) |
由战备完好率定义可知, 导弹装备战备完好率与任务通知时刻或上一任务结束时刻导弹装备状态及其维修能力有关, 是影响导弹装备持续作战能力和完成任务能力的重要指标之一. 从任务角度考虑,其可表示为: 在规定的使用及维修保障方案下, 能够执行任务的导弹数量与导弹总数量之比,其表达式为:
| \begin{equation}\label{5} {P_{OR}}=X \end{equation} | (5) |
1) 任务通知时刻处于完好状态的导弹在任务准备阶段不会发生故障;
2) 每枚导弹故障仅由一个LRU(现场可更换单元)故障引起, 即故障LRU数量与故障导弹数量是一一对应;
3) 所有SRU(车间可更换单元)修理时间均服从指数分布(对于故障定位来说指数分布比较合理);
4) 备件更换时间可忽略不计;
5) LRU的一次备件获取时间服从一般分布;
6) 任务通知时刻,导弹处于战备完好状态,则战备完好率为1;
7) 导弹因某一LRU故障处于不完好状态,且该LRU不可修复, 则导弹战备完好率为备件获取时间小于任务开始时间的概率;
8) 导弹因某一LRU故障处于不完好状态,且该LRU可修复, 则导弹战备完好率为该LRU的修复时间小于任务开始时间的概率. 2.2 单枚导弹战备完好率评估模型
设某型导弹包括$L$类LRU,第$l$类LRU故障率为$\lambda$, 在单枚导弹中的数量为${n_l}$,不可修复或报废的概率为${p_r}$,$1 \le l \le L$. 所有LRU的一次备件获取时间${t_g}$服从概率密度函数为$g(t)$ 的一般分布,则任务准备阶段可获得所需备件的概率为:
| \begin{equation}\label{6} {P_g} = P({t_g} \le {T_s}) = \int_0^{{T_s}} {g(t){\rm d}t} \end{equation} | (6) |
设第$l$类LRU的修复时间为${T^l}$,其修复过程分$r$ 个阶段进行,如图 1所示. 设第$l$($1 \le i \le r$)修复阶段的时间${T_i}$ 服从参数为${\mu _i}$的指数分布,在第$i$ 次故障定位后,底层故障SRU有备件可更换概率(即备件满足率)为${p_i}$.
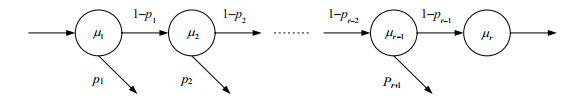 |
| 图 1 LRU的修复过程 |
当修复该LRU所需的所有SRU均无备件时, 该LRU的修复时间为所有修理阶段时间之和,其概率为:
| \begin{equation}\label{7} P\bigg({T^l} = \sum\limits_{i = 1}^r {{T_i}} \bigg) = \prod\limits_{i = 1}^{r - 1} {(1 - {p_i})} \end{equation} | (7) |
当修复LRU的第$k$层SRU有备件时,该LRU的修复时间为前$k$ 个故障定位阶段的时间,其概率为:
| \begin{equation}\label{8} P\bigg({T^l} = \sum\limits_{i = 1}^r {{T_i}} \bigg) = \prod\limits_{k = 1}^{k - 1} {(1 - {p_i})} {p_k},k = 1,2,\cdots, r \end{equation} | (8) |
由此可见,单个LRU修复过程服从库克斯分布. 根据库克斯分布的拉普拉斯变换, 某一LRU修复时间分布的拉普拉斯展开式为:
| \begin{equation}\label{9} \hat F(s) = \sum\limits_{i = 1}^r {\prod\limits_{j = 1}^i {(1 - {p_{j - 1}})} } {p_j}\frac{{{\mu _j}}}{{{\mu _j} + s}} \end{equation} | (9) |
利用反拉普拉斯变换得到修复时间的分布密度函数${f_l}(t)$. 通常LRU修理过程包括两阶段故障定位阶段与故障SRU修理阶段. 此时, LRU的修复时间分布的概率密度函数为:
| \begin{equation}\label{10} {f_l}(t) = {p_1}{\mu _1}{{\rm e}^{ - {\mu _1}t}} + (1 - {p_1}){\mu _1}{\mu _2}\frac{{{{\rm e}^{ - {\mu _1}t}} - {{\rm e}^{ - {\mu _2}t}}}}{{{\mu _2} - {\mu _1}}} \end{equation} | (10) |
设任务通知时刻导弹由于第$l$类LRU故障而处于不完好状态,且缺少第$l$ 类LRU备件的情况下,给定任务开始时间${T_s}$, 该LRU在任务开始时刻可修复好的概率为:
| \begin{equation}\label{11} P_t^l = P({T^l} \le {T_s}) = \int_0^{{T_s}} {{f_l}(t){\rm d}t} \end{equation} | (11) |
由此可得该导弹在任务开始时刻$T_s$的战备完好率为:
| \begin{equation}\label{12} {P_e}({T_s}) = {P_0} + (1 - {P_0})\bigg(\sum\limits_{l = 1}^L {P_c^l(P_r^l{P_g} + (1 - P_r^l)P_t^l)} \bigg) \end{equation} | (12) |
| \begin{equation}\label{13} P_c^l = {n_l}{\lambda _l}\bigg/\sum\limits_{l = 1}^L {{n_l}{\lambda _l}} \end{equation} | (13) |
设某部队有某型导弹总数为$M$枚,任务通知时刻故障导弹数量为$m$,包括$L$ 类LRU. 任务通知时刻$m$枚故障导弹中有$m_1$ 枚是因某LRU不可修复故障引起的,有$m_2$枚是可修复故障引起的,$m=m_1+m_2$,则 $m$枚故障导弹在任务开始时刻的战备完好率为$m_1$枚故障导弹备件获取时间与$m_2$ 枚故障导弹修复时间均小于任务开始时间$T_s$的概率. 对于$m_1$ 枚故障导弹备件获取时间小于任务开始时间的概率${P_g}$可根据公式(6)获得.
设$m_2$枚故障装备是由$m_2$个第$l$类LRU可修复故障引起的, 修复一个第$l$ 类LRU时间服从独立同分布的一般分布${F_l}(t)$, 其修理组数量为$c$.
当$1 < {m_2} \le c$时,$m_2$个第$l$类LRU修复时间为:
| \begin{equation}\label{14} {T^{({m_2},l)}} = \max \{ T_1^l,T_2^l,\cdots ,T_{{m_2}}^l\} \end{equation} | (14) |
| \begin{equation}\label{15} {F_{{m_2},l}}(t) = P({T^{({m_2},l)}} \le t)= \prod\limits_{i = 1}^{{m_2}} {P(T_i^l \le t) = {F_l}{{(t)}^{{m_2}}}} \end{equation} | (15) |
当${m_2} > c$时,设 ${\theta _i}(1 \le {\theta _i} \le {m_2}) $为${T^{({m_2},l)}}$ 时间内修理组$i$ ($1\le i\le c$)修复的故障件数量,且满足条件 ${m_2} = \sum_{i = 1}^c {{\theta _i}}$,$T_{{\theta _i}}^l$为修理组 $i$修复完第${\theta _i}$ 个故障件的时间,则有:
| \begin{equation}\label{16} {T^{({m_2},l)}} = \max \{ T_{{\theta _1}}^l,T_{{\theta _2}}^l, \cdots,T_{{\theta _c}}^l\} \end{equation} | (16) |
每个修理组修理过程是一个更新过程,则 ${T^{({m_2},l)}}$的分布为:
| \begin{equation}\label{17} {F_{{m_2},l}}(t) = P({T^{({m_2},l)}} \le t)= \sum\limits_{({\theta _1},{\theta _2},\cdots ,{\theta _c}) \in {S_{{m_2}}}} {P(\max \{ T_{{\theta _1}}^l,T_{{\theta _2}}^l,\cdots,T_{{\theta _c}}^l\} \le t)} =\\ \sum\limits_{({\theta _1},{\theta _2},\cdots ,{\theta _c}) \in {S_{{m_2}}}} {\prod\limits_{i = 1}^c {F_l^{{\theta ^*}}(t)} } \end{equation} | (17) |
当$m_2$ 枚故障装备是由不同的LRU(可修)故障引起时,修复时间的分布函数.
令 $J = \{ j|{m^j} \ne 0,1 \le j \le L\} $ 为所有故障LRU的类型, 有$1 \le \left| J \right| \le m$. 设 $m_2^j$ 是第$j$ 类LRU可修复故障的数量,且满足$0 \le m_2^j \le {m_2},\sum_{j = 1}^L {m_2^j} = {m_2}$,所有故障LRU的修复时间 ${T^{({m_2},J)}} = \mathop {\max }\limits_{j \in J} \{ {T^{(m_2^j,j)}}\}$, ${T^{(m_2^j,j)}}$ 为$m_2^j$ 个第$j$ 类LRU的修复时间,${T^{({m_2},J)}}$ 分布函数表示为:
| \begin{equation}\label{18} {F_{m,J(t)}} = P({T^{({m_2},J)}} \le t)= P\bigg(\mathop {\max }\limits_{j \in J} \{ {T^{(m_2^j,j)}}\} \le t\bigg)= \prod\limits_{j \in J} {{F_{m_2^j,j}}(t)} \end{equation} | (18) |
给定任务开始时间 $T_s$条件下,根据 ${T^{({m_2},l)}}$ 和${T^{({m_2},J)}}$的分布函数,可得到在任务开始之前修复 $m_2$个第$l$ 类LRU的概率为:
| \begin{equation}\label{19} P_t^{({m_2},l)} = P({T^{({m_2},l)}} \le {T_s}) = \int_0^{{T_s}} {{\rm d}{F_{{m_2},l}}(t)} \end{equation} | (19) |
修复$m_2$个不同类型LRU的概率为:
| \begin{equation}\label{20} P_t^{({m_2},l)} = P({T^{({m_2},J)}} \le {T_s}) = \int_0^{{T_s}} {{\rm d}{F_{{m_2},J}}(t)} = \prod\limits_{j \in J} {P_t^{(m_2^j,j)}} \end{equation} | (20) |
由此某型一批导弹在任务通知时刻有$m$ 枚处于故障状态条件下, 任务开始${T_s}$时刻可修复好的概率为:
| \begin{equation}\label{21} P({T_s}|m) = \sum\limits_{\left| J \right| = 1}^m {\sum\limits_{{m^j} \in S_m'} {\prod\limits_{j \in J} {{{(P_c^j)}^{{m^j}}}} } } {\sum\limits_{{m_2} = 0}^m {\sum\limits_{m_2^j \in S_{{m_2}}''} {\prod\limits_{j \in J} {{{(P_r^j)}^{{m^j} - m_2^j}}P_g^{{m^j} - m_2^j}{{(1 - P_r^j)}^{m_2^j}}P_t^{(m_2^j,j)}} } } } \end{equation} | (21) |
由此可得该批导弹在任务开始${T_s}$ 时刻的战备完好率:
| \begin{equation}\label{22} {P_e}({T_s}) = {P_0} + \sum\limits_{m = 1}^M {P({T_s}|m){P_m}} \end{equation} | (22) |
设导弹中某LRU故障间隔时间与修复时间分别服从均值为$1/\lambda$ 及$1/\mu $,变异系数平方为$C_a^2$、$C_r^2$的一般分布时, 可利用扩散过程求出系统的近似解.
在修LRU的数量 用连续变量 $x$代替,$f(x,t)$为$t$ 时刻扩散过程的位置的概率密度函数. 设$f(x) = \mathop {\lim }\limits_{t \to \infty } f(x,t)$, 根据扩散过程Fokker-Planck稳态方程可得:
| \begin{equation}\label{23} 0 = - \frac{\delta }{{\delta x}}[a(x)f(x)] + \frac{1}{2}\frac{{{\partial ^2}}}{{\partial {x^2}}}[b(x)f(x)] \end{equation} | (23) |
| \begin{equation}\label{24} f(x) = \frac{c}{{b(x)}}\exp \left[{2\int_0^c {\frac{{b(x)}}{{a(x)}}{\rm d}x} } \right] \end{equation} | (24) |
| \begin{equation}\label{25} a(x) = \left\{ {\begin{array}{*{20}{c}} {M\lambda - x\mu },& {0 \le x \le c} \\ {M\lambda - c\mu },& {c \le x \le S} \\ {(M - x + S)\lambda - c\mu },& {S < x \le S + M} \\ \end{array}} \right. \end{equation} | (25) |
| \begin{equation}\label{26} b(x) = \left\{ {\begin{array}{*{20}{c}} {M\lambda C_a^2 - x\mu C_r^2},& {0 \le x \le c} \\ {M\lambda C_a^2 - c\mu C_r^2},& {c \le x \le S} \\ {(M - x + S)\lambda C_a^2 - c\mu C_r^2} ,& {S \le x \le S + M} \\ \end{array}} \right. \end{equation} | (26) |
根据式(24)$\sim$(26)可得到$f(x)$,同理可求出 $S<c$情况下的$f(x)$. 系统中有$n$ 个故障件的概率为:
| \begin{equation}\label{27} {P_n} = \int_{n - 0.5}^{n + 0.5} {f(x){\rm d}x} ,n = 0,1,\cdots ,S + M \end{equation} | (27) |
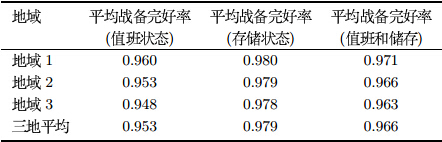
以我军现有代表性某型反舰导弹作为调研对象,选取三个典型储存地域进行调研, 包括检测记录、故障记录、修理记录和调动记录等信息,经过对调研数据整理分析, 得到该型导弹战备完好率统计数据如表 1所示,根据统计数据, 得到该型导弹战备完好率与服役年限的关系如图 2所示.
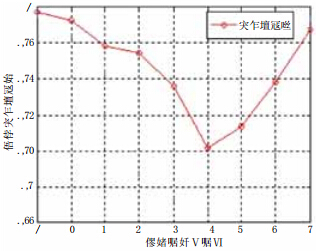 |
| 图 2 海军导弹战备完好性变化趋势图 |
根据图 2可以看出,导弹战备完好率变化趋势. 在服役1$\sim$4年内均能保持较高水平; 服役年限5$\sim$6年, 导弹在温、湿、振动等综合环境应力影响下,质量状态变差,完好率降低; 在经过5$\sim$7年期间的大中修之后,服役8$\sim$9年的导弹完好率增加. 3.2 调战备完好率评估验证
以现役某型典型反舰导弹为研究对象,来说明多级维修保障的导弹战备完好率模型. 该型导弹组成包括弹体、 制导系统、引战系统、动力系统、电气系统,从部队调研结果和前期导弹预防性维修研究看,弹体、引战、 电气系统故障率较低. 为简化求解,这里仅考虑故障率相对较高的雷达和自动驾驶仪两种设备.
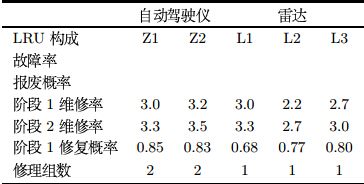
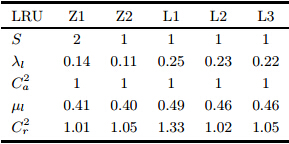
通过故障数据分析,自动驾驶仪主要故障单元为舵机与高度表, 分别记为Z1、Z2; 雷达主要故障单元为天线、晶体与电源, 分别记为L1、L2、L3. 雷达和自动驾驶仪的LRU修复过程均分为两个阶段, 即故障定位阶段与SRU修理或更换阶段. 两种设备的LRU构成、 两个阶段的修复率、SRU备件满足率及修理组数如表 2所示. 备件获取时间均服从参数为(1.5,2)的厄尔兰分布. 两种设备当前任务通知时刻前所有LRU的修复时间与任务准备阶段修复时间的分布相同, 故障间隔时间服从指数分布,所有LRU备件数量、 故障间隔时间与修复时间分布的均值与变异系数的平方见表 3. 不考虑上级维修保障资源时,根据上述的状态分析模型可以得到当前任务结 束时两种设备完好状态的概率分布见表 4. 假设当前任务结束时保障装备始终处于完好状态, 给定任务准备时间为1小时,求下一个任务开始 时导弹的战备完好率.
根据表 3数据以及公式(25)、(26),可得 $a(x),b(x)$, 通过归一化公式求出$f(x)$ 的值,进而得到 表达式, 利用式(27)得到计算结果如表 4所示.
假设对部件的维修分成两层,第一阶段是基层维修, 第二阶段是修理所维修,将表 2的阶段1维修率, 阶段2维修率和阶段1修复概率代入式(9),可得每种部件的维修时间分布.
将每种部件的维修时间分布,表 3的数据和表 4的结果数据代入到式(27)中, 得到下一个任务开始时雷达的战备完好率为98.68\%, 自动驾驶仪的战备完好率为97.36,根据模型(22),得 到下一个任务开始时该型号导弹的战备完好率为95.21\%.
该战备完好率计算结果与调研统计数据结果基本相符,如果考虑到具体设备维修等因素影响,此计算方法准确度更高,对于研究通过改进维修等方法提高导弹战备完好性水平具有借鉴意义. 4 结束语
本文对影响导弹装备战备完好性的重要参数战备完好率进行了研究,给出了战备完好率参数的定义,构建了基于扩散过程的导弹装备战备完好率评估模型, 并结合实际导弹装备服役信息的相关统计信息,有效地对该模型进行了评估验证, 证明了该方法评估导弹装备战备完好率的效果,为后续如何提出改进导弹装备战备完好率提供了借鉴.
| [1] | 李院生, 时和平. 装备战备完好性及其影响因素分析[J]. 电子产品可靠性与环境试验, 2007, 25(1): 38-41. Li Yuansheng, Shi Heping. Military equipment operational readiness and analysis of a affecting factors[J]. Electronic Product Reliability and Environmental Testing, 2007, 25(1): 38-41. |
| [2] | 花兴来, 刘庆华. 装备管理工程[M].北京: 国防工业出版社, 2002.Hua Xinglai, Liu Qinghua. Equipment Management Engineering[M]. Beijing: National Defense Industry Press, 2002. |
| [3] | 李刚, 陈国通, 蔡金燕,等. 电子装备战备完好性预测模型研究[J]. 现代电子技术, 2002(8): 62-64. Li Gang, Chen Guotong, Cai Jinyan, et al. The research of readiness argument method on surface to air missile[J]. Modern Electronic Technique, 2002(8): 62-64. |
| [4] | 刘冰, 朱小东, 王小魏. 装备战备完好性的模型预测研究[J]. 兵工自动化, 2005, 24(3): 8-9.Liu Bing, Zhu Xiaodong, Wang Xiaowei. Research on readiness simulation model of missile weapon system[J]. Ordnance Industry Automation, 2005, 24(3): 8-9. |
| [5] | 程文鑫, 陈立强, 龚沈光,等. 基于蒙特卡洛法的舰船装备战备完好性仿真[J].兵工学报, 2006, 27(6): 1090-1094.Cheng Wenxin, Chen Liqiang, Gong Shenguang, et al. Readiness simulation of ship equipment based on Monte-Carlo method[J]. Acta Armamentarii, 2006, 27(6): 1090-1094. |
| [6] | 魏勇, 徐廷学.基于任务的舰炮装备战备完好性建模与仿真研究[J]. 火炮发射与控制学报, 2010, 25(12): 15-18.Wei Yong, Xu Tingxue. Modeling and simulation research on operational readiness of naval gun weapon equipment based on mission[J]. Journal of Gun Launch & Control, 2010, 25(12): 15-18. |