0 引言
区域反导目标分配是针对大规模战术弹道导弹(tactical ballistic missile, TBM)进攻,按照一定的准则将一定数量的来袭TBM合理分配到区域部署的拦截系统以 实现拦截系统"高效分工"地拦截TBM,采取怎样的目标分配策略, 以达到最大的目标分配效果,是区域反导指控系统的核心模型之一[1, 2],其模型的科学与否直接决定了反导效能的高低.
武器目标分配问题是NP问题[3],模型的合理性及算法的Anytime特性[4]是影响区域反导目标分配的主要影 响因素.近年来,国内外学者从数学模型 及其求解算法进行不同的改进:从单一层防空扩展到多层防空,从仅考虑拦截效能到考虑时间、空间资源等方面的约束;从 静态目标分配到动态目标分配;求解 方法集中在群智能优化算法[5, 6, 7],其他智能优化算法[8, 9].目前常见的目标分配策略追求最大拦截效能,对于传 统的高炮,地空导弹武器系统数量 占优的防空作战,能达到较为理想的效果;对于部署有限的区域弹道导弹防御系统而言,容易导致所有火力单元的集中拦截 一枚TBM,容易占用甚至浪费宝贵的拦 截资源.为此,本文综合考虑作战效能和反导作战费用,尝试着建立综合拦截概率和最大化拦截效费比的目标分配模型,给出快 速收敛的克隆选择算法,深入探讨其 模型及算法设计与实现过程,并进行了仿真实验分析,力求为区域反导目标分配提供了科学参考. 1 区域反导目标分配问题描述
区域反导目标分配实质是在高实时,空域约束,拦截系统资源约束等多约束条件下,以来袭TBM相对区域保卫要地的威胁度为输入, 按照预定的分配准则,以实现 对TBM的期望拦截概率和拦截效能为目标,以来袭TBM分配到合适的高低两层拦截系统为输出的一种动态循环分配的过程,是区 域反导指控系统指挥控制高低两层 拦截系统实施拦截的核心环节.详细的目标分配循环流程见图 1.
 |
| 图 1 目标分配流程 |
由于弹道导弹进攻的突然性、高速性留给目标分配的时间极为有限,如图 1目标分配必须在时间区间$\left[ {t_1 ,t_2 } \right]$完成,这就对目标分配方案的精确性和求解的实时性提出了很高的要求,本文探讨基于目标分配流程构建的目标分配 模型及实时性强的模型求解算法.
防空目标分配常采取如下的目标分配准则:最大毁伤概率、最小消耗拦截弹、最大化拦截数目、上级指定等准则,分析以上目标分 配准则的适用情况以及单一 准则可能出现的资源浪费、准则失效、范围有限等不足,本文给出综合拦截概率和最大化拦截效费比的分配准则,具体描述如下:
1)总的原则是在一定期望拦截概率的条件下,最大化区域反导体系的作战效能,最小化拦截系统因发射拦截弹而消耗的费用; 2)优先保证威胁度大的目标分配给具有较大拦截概率的拦截系统,尽可能多次拦截,以达到期望的拦截概率; 3)保留一定的拦截弹资源用于后续的反导作战. 2 区域反导目标分配模型 2.1 符号说明
本模型采用的符号及其意义见表 1.
拦截决策变量,见式(1).
| \begin{equation} \label{eq10} \begin{array}{l} X_{p,i,t} =\left\{ {\begin{array}{l} 1 , ~p\in P~\mbox{层第}~i~\mbox{个拦截系统拦截第}~t~\mbox{个}~TBM\\ 0 ,~ p\in P~\mbox{层第}~i~\mbox{个拦截系统不拦截第}~t~\mbox{个}~TBM\\ \end{array}} \right. \\ \end{array} \end{equation} | (1) |
1) 威胁度更新
由于TBM每次遭到拦截后的威胁度都会降低,本文采用威胁度更新机制,当被某一拦截系统拦截后,第$t$个TBM的威胁度$value_m^t $按照式(2)更新.
| \begin{equation} value_m^t (new)=value_m^t (old)\cdot \prod\limits_{p\in P,i\in force_p } \end{equation} |
| \begin{equation} {(1-S_{p,i,t} X_{p,i,t} Pk_{p,m} )} ,\ \forall t\in \sum\limits_{m\in M} {missile_m } \end{equation} | (2) |
${\small 1}$ 目标函数
区域反导作战既要追求最大化地消耗来袭TBM的威胁度,又追求最小化的作战费用;为此采取拦截效能与作战代价的比值作为目标函数. ${\small 2}$ 约束条件
目标分配的约束条件主要有4个:
• 区域高低两层每个拦截系统可发射拦截弹的数量约束;
• 上级对每枚TBM期望拦截概率;
• 射击有利度小于阈值$\varepsilon $的拦截系统不具备拦截条件,不能发射拦截弹;
• 保证每枚TBM都被拦截.
具体的目标分配模型见式(3).
| \begin{equation} \begin{array}{l} \max \left\{ {\frac{\sum\limits_{t\in \sum\limits_{m\in M} {missile_m } } {value_m^t \cdot \prod\limits_{p\in P,i\in force_p } {(1-S_{p,i,t} X_{p,i,t} Pk_{p,m} )} } }{\sum\limits_{p\in P} {\left( {cost_p \cdot \sum\limits_{i\in force_p } {\sum\limits_{t\in \sum\limits_{m\in M} {missile_m } } {X_{p,i,t} } } } \right)} }} \right\} \\ \\ \mbox{s.t. }\left\{ {\begin{array}{l} \sum\limits_{t\in \sum\limits_{m\in M} {missile_m } } {X_{p,i,t} } \le anti\mbox{-}missle_{p,i} \mbox{ }\forall p\in P,i\in force_{p,c} \\ 1-\prod\limits_{p\in P,i\in force_p } {(1-S_{p,i,t} X_{p,i,t} Pk_{p,m} )} \ge Ph_t \mbox{ }\forall t\in \sum\limits_{m\in M} {missile_m } \\ \mbox{if}\ \mbox{ }S_{p,i,t} <\varepsilon ,\mbox{ }X_{p,i,t} =0\mbox{ }\forall p\in P,i\in force_{p,c} ,t\in \sum\limits_{m\in M} {missile_m } \\ \sum\limits_{p\in P} {\sum\limits_{i\in force_p } {X_{p,i,t} >0\mbox{ }\forall t\in \sum\limits_{m\in M} {missile_m } } } \\ P\mbox{=}\left\{ {\left. {1,2} \right\} } \right.,M\mbox{=}\left\{ {1,2} \right\} \\ \end{array}} \right. \\ \end{array} \end{equation} | (3) |
该模型的决策变量是$X_{p,i,t} $,只能取0或1,该模型实质是三维上扩展的0-1规划模型.为了提高模型的适应性和方便求解问题,可将三维数的0-1规划转化为二 维的0-1规划,分为以下两步进行操作:
首先,认为同一TBM可以分配给不同拦截系统,则目标分配方案$Y$表示为式(4).
| \begin{equation} \label{eq4} \begin{array}{lll} Y&\hspace{-4mm}=\left[{y_{ij} } \right]_{( {\sum\limits_{m\in M} {missile_m } } )\times ( {\sum\limits_{p\in P} {force_p } } )} \\ &\hspace{-4mm}=\left[{{\begin{array}{*{20}c} {y_{11} } \hfill & {y_{12} } \hfill & \cdots \hfill & {y_{1( {\sum\limits_{p\in P} {force_p } } )} } \hfill \\ {y_{21} } \hfill & {y_{22} } \hfill & \cdots \hfill & {y_{2( {\sum\limits_{p\in P} {force_p } } )} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {y_{( {\sum\limits_{m\in M} {missile_m } } )1} } \hfill & {y_{( {\sum\limits_{m\in M} {missile_m } } )2} } \hfill & \cdots \hfill & {y_{( {\sum\limits_{m\in M} {missile_m } } )\times ( {\sum\limits_{p\in P} {force_p } } )} } \hfill \\ \end{array} }} \right] \\ \end{array} \end{equation} | (4) |
| \begin{equation} \label{eq5} 0\leq y_{ij} \leq anti\mbox{-}missle_{p,i} \end{equation} | (5) |
| \begin{equation} \label{eq6} 0\leq \sum\limits_{i=1}^{( {\sum\limits_{m\in M} {missile_m } } )}{y_{ij} } \leq anti\mbox{-}missle_{p,i} \end{equation} | (6) |
然后,为转化为基本0-1规划,可将同一拦截系统的所有可发射拦截弹看成部署在同一位置具有相同性能但相互独立的拦 截弹,目标分配方案$Y$可表示为式(7).\newpage \topskip -5mm
| \begin{equation} \label{eq7} \begin{array}{l} Y=\left[{y_{ij} } \right]_{( {\sum\limits_{m\in M} {missile_m } } )\times ( {\sum\limits_{p\in P} {\sum\limits_{i\in force_p } {anti\mbox{-}missle_{p,i} } } } )} \\ =\left[{{\begin{array}{*{20}c} {y_{11} } \hfill & {y_{12} } \hfill & \cdots \hfill & {y_{1( {\sum\limits_{p\in P} {store_p } } )} } \hfill \\ {y_{21} } \hfill & {y_{22} } \hfill & \cdots \hfill & {y_{2( {\sum\limits_{p\in P} {store_p } } )} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {y_{( {\sum\limits_{m\in M} {missile_m } } )1} } \hfill & {y_{( {\sum\limits_{m\in M} {missile_m } } )2} } \hfill & \cdots \hfill & {y_{( {\sum\limits_{m\in M} {missile_m } } )\times ( {\sum\limits_{p\in P} {store_p } } )} } \hfill \\ \end{array} }} \right] \\ \end{array} \end{equation} | (7) |
此时拦截决策变量是$y_{ij} \in \left\{ {0,1}\right\}$, 0表示第$j$个拦截弹不拦截第$i$个TBM, 1表示第$j$个拦截弹拦截第$i$个TBM.此时的目标分配方案$Y$与原来目标分配方案$X$一一映射, 从而将复杂三维的0-1规划问题转化为基本0-1规划问题. 3 快速收敛的克隆选择算法
由构建的模型可知,区域反导目标分配问题属于多个约束条件的非线性优化问题,该类问题的求解算法以智能优化算法为主.克隆选择算法 (clonal selection algorithm, CLONALG)作为简单模拟免疫效应的智能优化算法已经广泛应用于组合优化等领域,然而基本的克隆选择算法 容易出现早熟收敛的情况,因此本文结合生物免疫系统抗体多样性和免疫记忆的特征,深入分析免疫记忆机制,克隆机制,自适 应策略,免疫抑制 机制,种群更新机制,从增加种群多样性的角度,改进CLONALG,提出了快速收敛于全局最优解的快速收敛的克隆选择算法(fast convergence clonal selection algorithm,FCCSA),力求提高算法的多模态优化问题的求解能力,提高解的精度和求解速度. 3.1 FCCSA设计
下面从以下几个方面改进CLONALG.
1) 克隆算子
抗体受抗原的侵入刺激被激活,克隆增值;同时抗体之间的竞争抑制作用维持免疫平衡.传统的比例克隆不能体现此机制,改进 的克隆算子对其进行模拟, 克隆规模依据抗体-抗原的亲和力、抗体-抗体的亲和度自适应的调整.为此,先定义抗体$i$与其他抗体的亲和度$\Phi_i $,见式(8).
| \begin{equation} \label{eq8} \Phi _i =\min \left( {\exp \left( {\left\| {\left. {X_i -X_j } \right\|} \right.} \right)} \right),i\ne j,i,j=1,2,\cdots,n \end{equation} | (8) |
| \begin{equation} \label{eq9} k_i ={\rm Int}\left[{k\ast \Phi _i \ast \frac{f\left( {X_i } \right)}{\sum {f\left( {X_i } \right)} }} \right] \end{equation} | (9) |
2) 云自适应变异算子
CLONALG用于求解复杂优化问题时,变异算子在该算法中显得尤其重要[10].对克隆扩增后的抗体群中每个抗体进行变异可提 高抗体的多样性,扩大搜索的范围,以寻找更优秀的抗体.云模型用期望值$Ex$、熵$En$和超熵$He$表征定性概念,将概念的模糊 性和随机性集成在一起,为定性与定量相结合的信息处理提供了有力手段.期望值$Ex$反映了云层的重心位置; $En$反映了云层的 陡峭程度, $En$越小越陡峭;超熵$He$反映了云层的厚度, $He$越大云层越厚[11, 12],见图 2.
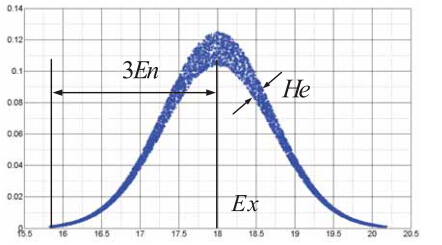 |
| 图 2 正态云模型的3个数字特征示意图 |
当$x>Ex$时,确定度随$x$的增大而减小,云模型中云滴集中在区间$\left[{Ex-3En,Ex+3En}\right]$,具有随机性和稳定倾向, 把云模型的这一特征应用于抗体变异的控制.亲和力小的抗体进行较大的变异,以求生成亲和力大的抗体,反之,要求变异 较小,以保护优良抗体.
令$Ex=f_{{\rm avg}} $,$En=\frac{\left( {f_{\max } -f_{{\rm avg}} } \right)}{e}$,$He=\frac{En}{h}$,$En'=randn\left( {En,He} \right)$.
对于抗体$X=\left[{x_1 ,x_2 ,\cdots,x_n } \right]$经过变异后得到$X^\prime=\left[{x^\prime_1 ,x^\prime_2 ,\cdots,x^\prime_n } \right]$,则新抗体$X^\prime$的组成元素见式(10).
| \begin{equation} x^\prime_i =x_i +\alpha _i N_i \left( {0,1} \right)\varphi \left( f\right),i=1,2,\cdots,n \end{equation} |
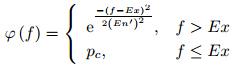 | (10) |
$e$、$h$为控制参数, $e$用来控制云的陡峭程度,根据"$3En$"规则,一般去3, $h$用来控制云层的厚度,一般去10,$\alpha _i $、$p_c $为特定的参数,实验中根据具体情况调整.
3)抗体重组算子
抗体在亲和度成熟的过程中,抗体重组也是增加抗体多样性的主要方式,借鉴遗传算法交叉的思想,引入抗体重组算 子.设三个独立的父代抗体$s_1 $、$s_2 $、$s_3 $杂交生成子代抗体$s_c $,其中$s_c $满足式(11)
| \begin{equation} \label{eq11} s_c =\frac{k_1 \cdot s_1 }{k_1 +k_2 +k_3 }+\frac{s_2 \cdot k_2 }{k_1 +k_2 +k_3 }+\frac{s_3 \cdot k_3 }{k_1 +k_2 +k_3 } \end{equation} | (11) |
云自适应变异算子、抗体重组算子的共同作用,实现了抗体间的信息交流、协同进化,使得克隆后的抗体群在亲 和力高的抗体周围分散开,大大增加了抗体群的多样性,使得算法在已有优良抗体的基础上,通过亲和度成熟过程, 以较高的概率找到更优秀的抗体,提高算法的收敛速度.
4)精英抗体保存算子
为减少冗余计算,建立记忆种群,将多个优良抗体直接放在记忆种群中,启发抗体群收敛的方向,为快速收敛得到全局最优解提供保障. 3.2 求解流程
下面给出算法求解模型的执行步骤:
Step 1 启发式方法生成规模为$q$的初始抗体群$X\left( 0 \right)=\left\{ {X_1 ,X_2,\cdots,X_q } \right\}$;
Step 2 精英抗体保存算子:在抗体群$X\left( t \right)$中选择$m$个抗体-抗原亲和力最大的抗体,加入记忆种群$X_m \left( t \right)$;
Step 3 克隆算子:对记忆种群$X_m \left( t \right)$依据式(9)实施克隆后的抗体群为$X^c\left( t \right)=\left\{ {X^c_1 ,X^c_2 ,\cdots,X^c_q } \right\}$,$X^c_i $ 为个体$X_i $的克隆子群;
Step 4 云自适应变异算子:对抗体群$X^c\left( t \right)$依据式(10)对抗体的每个基因进行云自适应变异,生成抗体群$X^\ast \left( t \right)$;
Step 5 随机选取三个抗体按照抗体重组算子进行操作,最后生成抗体群$X^r\left( t \right)$;
Step 6 合并抗体群$X^\ast \left( t \right)$和$X^r\left( t \right)$,生成抗体群$X^l\left( t \right)$;
Step 7 抗体群更新操作:随机产生$d$个新抗体,替换抗体群$X^l\left( t \right)$中亲和力较小的抗体;
Step 8 终止判断.若不满足迭代次数,则更新迭代代数记数器$t\to t+1$,并选取抗体群$X^l\left( t \right)$的$m$个亲和力较大的抗体组成下一代抗体群$X_m \left( t \right)$,然后转入到Step 3;否则,输出结果,算法结束.
算法结束后,记忆种群中的抗体即为所求问题的解. 4 仿真分析 4.1 仿真条件
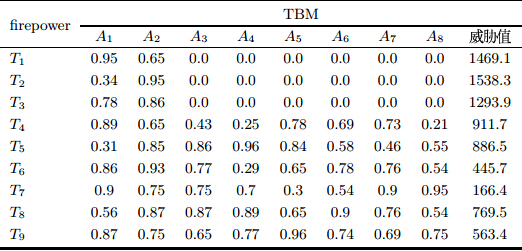
要求某波次共9批TBM被摧毁的最低概率为0.9.区域各拦截系统 (firepower)及来袭TBM相关参数见表 2、表 3,表中缩写含义:中程弹道导弹 (middle-range ballistic missile,MRBM)、近程弹道导弹(short-range ballistic missile,SRBM).
表 3中的参数说明如下: $A_i $: 第$i$个拦截系统,其中,$A_1 \sim A_2 $、$A_3 \sim A_8 $分别是区域高层、低层拦截系统; $T_i $: 第$i$个来袭TBM,$T_1 \sim T_3 $是MRBM,$T_4 \sim T_9 $是SRBM. 仿真参数设定$cgmax=300$,$G=30$,$m=10$,$n=150$,$p_{c\max }\mbox{=0.9}$,$ p_{m\max } \mbox{=0.4}$,$p_{c\min } \mbox{=0.1}$,$p_{m\min } \mbox{=0.01}$,$d\mbox{=10}$, $Penalty=10^{-6}$,$L=3$. 4.2 仿真结果
基于Matlab语言编程实现,分别用混沌克隆选择算法 (chaos clonal selection algorithm,CCSA)、\\ CLONALG仿真,每种算法运行30次, 每次迭代300次,取10组最好的作为样本,仿真结果见图 3,其中横坐标表示迭代次数 (iterationtimes),纵坐标表示10组样本各迭代次数下的所得种群的最大适应度 (fitness)的平均.
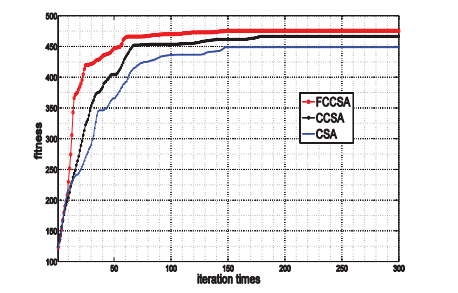 |
| 图 3 最大适应度随着迭代次数的变化 |
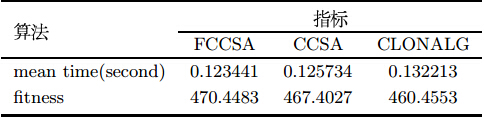
按照如下操作修改源程序,调用Matlab中的计时器函数tic、toc,三种算法收敛时跳出循环,得到计算10组样本数据平均时间 (mean time)和适应度值,见表 4.
为了更直观地反映算法的寻优效果,借鉴文献[13]中种群多样性指标来衡量优化算法的寻优能力,种群 多样性是指种群中个体的差异性,多样性缺失的直接结果就是搜索可能陷入一个不含全局最优点的区域 难以逃离,这就是早熟问题.定义如式(12)的种群多样性指标.
| \begin{equation} PDM=\frac{f\left( {A_{m,n} } \right)_{{\rm avg}} }{f\left( {A_{m,n} } \right)_{\max } } \end{equation} | (12) |
式(12)中$f\left( {A_{m,n} } \right)_{{\rm avg}} $、$f\left( {A_{m,n} } \right)_{\max } $分别表示当代种群个体的平均适应度值和最大适应度值. $PDM\in \left[ {0,1} \right]$,当算法收敛时,其值趋于1.
此三种算法的种群多样性结果如图 4.
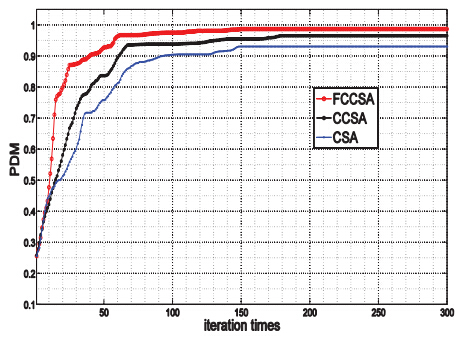 |
| 图 4 种群多样性随着迭代次数的变化 |
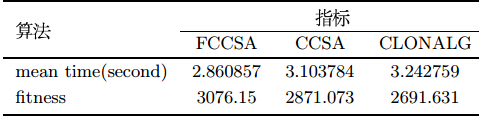
增加目标分配的规模:设置来袭15批MRBM,45批LRBM,分别在[1100 1500]、[400 1000]之间随机生成MRBM、LRBM的威胁估计值,区域高层、低层拦截系统的数量分别为6、30,在$\left[ {0.5,0.9} \right]$之间随机生成各拦截系统对TBM的射击有利度,其他仿真参数不变.基于三种算法进行仿真得 到种群多样性结果如图 5;算法收敛时的平均时间和适应度值见表 5.
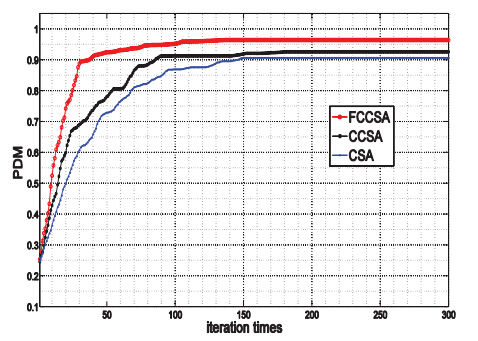 |
| 图 5 增加目标分配规模时的种群多样性比较 |
图 3$\sim $图 5、表 4$\sim $表 5的结果表明, FCCSA求解精度和求解速度均高于CCSA、CLONALG,种群多样性大大增加,收敛速度较快,当目标分配规模较大时, FCCSA不容易陷入局部最优,这种全局搜索能力、时间性能尤为突出.由于区域反导作战过程时间很短暂,从而目标分配对实时性 要求极高, FCCSA作为一种寻优速度高和寻优能力强的优化算法,不失为区域反导目标分配模型较为理想求解算法.
TBM进攻的突然性、高速度等特性留给目标分配的时间极为短暂,因而探索实时性更强的智能优化算法是目 标分配模型求解的必然需求之一, 本文旨在目标分配时间区间$\left[{t_1 ,t_2 }\right]$之内探索寻优能力强的优化算法,一旦超出目标分配时 间区间,超出前的目标分配方案 即使不是最优,也作为最终的目标分配方案分配下去,以满足后续拦截规划的时间约束需求.
| [1] | 肖金科,王刚,付强,等.反导C2BM技术体系结构研究[J].飞航导弹, 2012, 9: 57-61.Xiao Jinke, Wang Gang, Fu Qiang, et al. Research on technology requirement of C2BM in anti-missile system[J]. Aerodynamic Missile Journal, 2012, 9: 57-61. |
| [2] | 肖金科,王刚,刘昌云,等. DoDAF的末段反导C2BM系统需求分析[J].火力与指挥控制, 2013, 38(8): 13-17.Xiao Jinke, Wang Gang, Liu Changyun, et al. Research on requirement analysis of C2BM in terminal anti-missile system based on DoDAF[J]. Fire Control & Command Control, 2013, 38(8): 13-17. |
| [3] | Hosein P A, Athans M. Some analytical results for the dynamic weapon-target allocation problem[R]. Cambridge, MA: Massachu-setts Institute of Technology, 1990: 1-28. |
| [4] | 吴玲,卢发兴. WTA问题的截止期定义及Anytime算法分析[J].武汉理工大学学报, 2010, 32(6): 140-143.Wu Ling, Lu Faxing. Analysis of deadlines and anytime algorithms for weapon-target allocation problem[J]. Journal of Wuhan University of Technology, 2010, 32(6): 140-143. |
| [5] | 黄峰,陈中起,冯金富,等.基于半约束随机搜索的空舰导弹目标分配方法[J].系统工程与电子技术, 2013, 35(8): 1676-1680.Huang Feng, Chen Zhongqi, Feng Jinfu, et al. Target assignment algorithm for air-to-ship missile based on semi-restraint stochastic searching[J]. Systems Engineering and Electronics, 2013, 35(8): 1676-1680. |
| [6] | 王一川,单甘霖,童俊.基于协同memetic PSO算法的传感器-目标分配问题求解[J].系统工程与电子技术, 2013, 35(5): 1000-1007.Wang Yichuan, Shan Ganlin, Tong Jun. Solving sensor-target assignment problem based on cooperative memetic PSO algorithm[J]. Systems Engineering and Electronics, 2013, 35(5): 1000-1007. |
| [7] | 刘晓,刘忠,侯文姝,等.火力分配多目标规划模型的改进MOPSO算法[J].系统工程与电子技术, 2013, 35(2): 326-330.Liu Xiao, Liu Zhong, Hou Wenshu, et al. Improved MOPSO algorithm for multi-objective programming model of weapon-target assignment[J]. Systems Engineering and Electronics, 2013, 35(2): 326-330. |
| [8] | 杨晓凌,邱涤珊,彭黎,等.改进类电磁算法在武器目标分配问题中的应用[J].国防科技大学学报, 2011, 33(6): 150-153.Yang Xiaoling, Qiu Dishan, Peng Li, et al. Application of modeling electromagnetism-like algorithm in weapon-target assignment problem[J]. Journal of National University of Defense Technology, 2011, 33(6): 150-153. |
| [9] | 罗江锋,朱承,崔婧,等.舰艇防空火力规划与调度方法研究[J].国防科技大学学报, 2013, 35(2): 40-45.Luo Jiangfeng, Zhu Cheng, Cui Jing, et al. Planning and scheduling for the air defense of warship[J]. Journal of National University of Defense Technology, 2013, 35(2): 40-45. |
| [10] | 陈乃建,张进华,王孙安,等.基于克隆选择的小世界优化算法[J].中南大学学报(自然科学版), 2012, 43(8): 3091-3098.Chen Naijian, Zhang Jinhua, Wang Sunan, et al. Small-world optimal algorithm based on clone selection[J]. Journal of Central South University (Science and Technology), 2012, 43(8): 3091-3098. |
| [11] | 吴立锋,程林辉.基于云自适应遗传算法的改进BP算法[J].中南民族大学学报(自然科学版), 2011, 30(4): 98-101.Wu Lifeng, Cheng Linhui. An improved BP algorithm based on cloud self-adaptive genetic algorithm[J]. Journal of South-Central University for Nationalities (Natural Science Edition), 2011, 30(4): 98-101. |
| [12] | 董丽丽,龚光红,李妮,等.基于云模型的自适应并行模拟退火遗传算法[J].北京航空航天大学学报, 2011, 37(9): 1132-1136.Dong Lili, Gong Guanghong, Li Ni, et al. Adaptive parallel simulated annealing genetic algorithms based on cloud models[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(9): 1132-1136. |
| [13] | 韩飞,杨春生,刘清.一种改进的基于梯度搜索的粒子群优化算法[J].南京大学学报(自然科学版), 2013, 49(2): 196-201.Han Fei, Yang ChunSheng, Liu Qing. An improved particle swarm optimization based on gradient search[J]. Journal of Nanjing University (Natural Sciences), 2013, 49(2): 196-201. |