2. 中国船舶工业系统工程研究院, 北京 100094;
3. 中国科学院 数学与系统科学研究院, 北京 100190
2. Systems Engineering Research Institute, China State Shipbuilding Corporation, Beijing 100094, China;
3. Academy of Mathematics and Systems Science, ChineseAcademy of Sciences, Beijing 100190, China
0 引言
机群保障是指在各种保障技术工艺约束下, 对多批次、多架次飞机同时进行保障,从而快速形成作战能力. 机群保障资源配置优化问题涉及到多架飞机、多种资源在多个作业阶段的有效协调, 是一个超大规模且具有多约束的优化问题. 其约束包括保障装备、资源、业务逻辑、工艺顺序等. 通过产生满足约束的优化调度解, 机群保障资源配置优化旨在高效地辅助制定从现在起至未来一段时间内的详细的机群保障计划, 即对机群保障的工序流程进行合理安排, 确定各飞机执行保障的工序任务、各保障工序使用的资源、开工及完工时间信息等.
传统的机群资源配置调度大多基于人工经验. 但随着保障工艺过程愈加复杂、需要保障的机群规模增大, 对调度的实时性、鲁棒性要求提高, 人工调度在实际机群保障中面临着越来越多的瓶颈和挑战. 具体而言, 人工调度很难科学、合理地实现现场多工序、多资源的生产调度; 缺乏在前期接收任务时对调度问题的整体评估; 无法了解某资源在某个时段是否会产生瓶颈, 无法为计划安排、计划协调提供决策依据; 任务的多样性、复杂性、紧迫性以及较大的调度规模也使得人工调度很难保证解的次优性, 甚至可行性[1].
国内学者已在车辆调度、卫星成像调度、集装箱码头调度、侦察任务调度、火力在线调度、天基预警调度方法等领域做了不少研究工作. 李妍峰等[2]研究了节点行驶时间与距离和所处时段相关的时变车辆调度问题, 提出了一种满足先入先出准则的跨时段方法,构造了动态规划启发式算法,数值结果表明该算法能较好地平衡求解质量和运行时间. 针对成像 侦察卫星应急调度问题,贺川等[3]构建了多星调度的约束满足模型,采用周期驱动与事件驱动相结合的调度优化策略,并将滚动优化调度算法 和启发式算法结合用于求解多星应急调度问题. 孙彬等[4]考虑了不确定性环境下的集装箱码头调度问题,将该问题分解为泊位和岸桥联合实时调度两部分,分别采用ASAP(As soon as possible)策略和MAS(multi-agent system)技术,利用CNP(contract-network-protocol)求解实时调度问题,仿真结果表明提出的调度策略更具鲁棒性. 针对不确定环境下UAV侦察任务调度问题,王小乐等[5]建立了任务执行过程的状态转移模型来反映任务调度顺序对代价和收益的影响,并推导出了任务降序排列调度策略的最优性. 仿真结果表明,该算法比遗传算法和穷举搜索算法更高效. 罗江锋等[6]构建了连续多目标来袭的舰艇防空火力调度模型,通过在线仿真验证了基于重调度模型的有效性. 姜维等[7]研究了面向天基预警过程的复杂多传感器跟踪任务调度问题,建立了基于信息增益的多目标预警优化调度模型,设计了基于免疫克隆选择算法的分布式并行调度求解算法,基于HLA的仿真结果表明了该模型和算法的有效性和鲁棒性.
作为一类非常重要的资源约束调度问题[8, 9],机群保障资源配置建模与优化研究也得到了国内 相关学者的关注并取得了一定进展. 针对机群面向作战任务的实时动态综合保障需求, 冯强等[10]分析了机群使用保障与维修保障的基本过程, 探讨了有限资源约束下的动态调度特征, 建立了三层混合控制的多主体模型架构, 给出了机群动态保障的有限资源调度算法. 以飞机的战备完好性指标、单位时间出动架次为优化目标, 选取飞机的典型任务模式对模型进行了验证. 林华等[11]考虑机群回收过程中的飞行甲板跑道容量瓶颈问题, 对三种常见的排序算法, 即先来先服务、基于最早到达时刻、滑动窗算法进行了比较, 仿真结果表明滑动窗排序法排序结果最好. 杨炳恒等[12]分析了机群调运作业时序, 提出了一种机群调运作业流程交通网模型, 为机群调运作业时序提供了优化建议.
本文系统分析了机群保障的基本流程,厘清了保障过程中的各类约束条件, 明确了机群保障资源配置的优化目标, 构造了机群保障资源配置的数学优化模型. 针对机群保障资源配置问题的大规模性与NP-hard性,采取滚动调度思想, 将大规模优化问题分解为若干子问题,进而提高了求解的效率. 最后以4架飞机6批次连续出动作为典型任务模式, 基于优化平台验证了模型和算法的有效性和高效性. 本研究从数学建模的角度对多波次多架飞机的保障全工艺流程进行了建模. 同时, 本研究为机群保障资源配置优化问题提供了一种有效的解决思路. 1 机群保障资源配置问题 1.1 问题描述
机群保障中,需要对多架飞机同时执行保障,而每架飞机涉及到上百道工序, 需要诸多消耗性资源与相应的保障设备. 由于资源有限, 为了使机群能够快速执行任务,形成作战能力, 需要对资源进行合理的分配与调度,从而实现对机群的高效保障. 机群保障资源配置问题是指在满足诸多约束条件下, 以最晚完工保障工序时间最小化为优化目标, 确定各飞机各保障工序执行的时间及所需要的资源等. 从数学角度而言, 机群保障资源配置问题属于一类大规模的NP-hard问题. 我们也注意到实际保障过程中存在不确定因素, 比如飞机战损、设备故障等. 本文只考虑确定性情况下的多机保障资源配置问题. 1.2 主要约束 1.2.1 资源约束
由于受多种因素限制, 资源(人员、设施、设备与物资等)成为机群保障的重要制约因素. 通常可将资源划分为三类,即: 可更新资源、消耗性资源和双重限制资源[13, 14]. 可更新资源指的是在保障过程中不会损耗的资源, 也就是数量不会减少的资源,比如人员和设备等. 尽管人员通过休息可以具备继续工作的能力, 设备通过计划检修也可以维持工作状态, 但可更新资源在每个时刻的数量是有限的. 消耗性资源指的是保障过程中不断被消耗的资源, 如弹药、备件、电燃气液等. 使用该类资源不能超出其初始供应总量的限制. 双重限制资源, 是指那些既可以作为可更新资源亦可作为消耗性资源的资源. 不失一般性, 模型中通常只考虑可更新资源和消耗性资源. 此外, 部分保障工序加工需要多类资源,部分工序加工则不需要资源等. 1.2.2 飞机约束
机群保障作业流程复杂,涉及到起飞、降落、调运、电燃气液保障、弹药保障等专项作业. 在执行各项保障任务时,飞机需要在不同的保障站位之间移动, 此时需要考虑飞机在不同保障站位之间的移动时间约束. 由此可得: 同一架飞机后续工序开工时间应该大于或等于前继工序的完成时间与飞机在这两个保障站位间的移动时间之和. 1.2.3 业务逻辑约束
不同类型的飞机具有不同的保障作业流程, 且提炼出来的保障工序前后继关系包括串行、入树和出树. 除此之外, 保障工序还受特殊的时间窗约束条件制约[15],包括: 1)头尾方式, 即前继工序完工一定时间内,其后续工序才能开工; 2)头头方式, 即前继工序开工一定时间内,其后续工序才能开工; 3)尾尾方式, 即前继工序完工一定时间内,其后续工序必须完工. 2 机群保障资源配置调度数学模型 2.1 符号描述
通过上述的对机群保障资源配置问题的约束分析,定义如下符号:
• $I$: 飞机集合;
• $m=|I|$: 飞机数量;
• $J_{i}$: 第$i$架飞机所需进行的保障工序总数; %
• $J_{i}^{+}$: 第$i$架飞机包含保障开始和结束的两个虚任务的任务集合;
• $P$: 工位集合;
• $n=|P|$: 工位数量;
• $p_{ij}$: 第$i$架飞机第$j$道工序所在的工位;
• $d_{ij}$: 第$i$架飞机第$j$道工序的工期;
• $T=\sum\limits_{i \in I}\sum\limits_{j \in J_{i}^{+}}d_{ij}$;
• $P_{ij}$: 第$i$架飞机第$j$道工序的前驱任务集合;
• $S_{ij}$: 第$i$架飞机第$j$道工序后继任务集合;
• $J(t)$: 在时刻$t$处于执行状态的工序集合;
• $NR$: 可更新资源的种类数;
• $NR_{k}$: 可更新资源$k$的数量;
• $r_{ijk}$: 第$i$架飞机第$j$道工序所需可更新资源$k$的数量;
• $NN$: 消耗性资源的种类数;
• $NN_{l}$: 消耗性资源$l$数量;
• $n_{ijl}$: 第$i$架飞机第$j$道工序所需消耗性资源$l$的数量;
• $dist(p_{1},p_{2})$: 工位$p_1$与$p_2$之间的距离;
• $\nu_{i}$: 第$i$架飞机的标准移动速率;
• $p_{ij}^{FS}$: 第$i$架飞机第$j$道工序的最小完成-开始滞后时间;
• $x_{ijt}=\left\{ \begin{matrix} 1,& \mbox{第$i$架飞机第$j$道工序在时刻$t$完成},\\ 0,& \mbox{否则}. \\ \end{matrix} \right.$ 2.2 机群保障资源配置数学模型
| \begin{eqnarray} \min && \max\limits_{i\in I,j\in J_{i}} \sum\limits_{t=0}^{T}tx_{ijt} \end{eqnarray} | (1) |
| \begin{eqnarray} \mbox{s.t.} && \sum\limits_{i\in I}\sum\limits_{j\in J(t)} r_{ijk}\le r_{k},\forall k \in NR,t\in [0,T] \end{eqnarray} | (2) |
| \begin{eqnarray} \sum\limits_{i\in I} \sum\limits_{j\in J_{i}} n_{ijk}\le n_{l},\forall l \in NN \end{eqnarray} | (3) |
| \begin{eqnarray} && \sum\limits_{t=0}^{T} x_{ijt}=1,\forall i\in I,j\in J_{i} \end{eqnarray} | (4) |
| \begin{eqnarray} \sum\limits_{t=0}^{T}t x_{iht}+\frac{dist(p_{ih},p_{ij})}{v_{i}} \le \sum\limits_{t=0}^{T}(t-d_{ij}) x_{ijt},\forall h\in P_{ij},i\in I,j\in J_{i} \end{eqnarray} | (5) |
| \begin{eqnarray} \sum\limits_{t=0}^{T} t x_{iht}+p_{ij}^{FS}\le \sum\limits_{t=0}^{T}(t-d_{ij}) x_{ijt}, \forall i\in I,j\in J_{i},h\in P_{j} \end{eqnarray} | (6) |
| \begin{eqnarray} x_{ijt}\in \{0,1\},\forall i\in I,j\in J_{i},t\in [0,T] \end{eqnarray} | (7) |
目前关于优化求解的软件有很多,代表性的有: Cplex,Xpress,Gurobi,GAMS,LINGO,LINDO,CONOPT等.
本研究所针对的机群保障资源配置优化调度问题是典型的NP-Hard问题, 不存在精确求解该类问题的多项式算法. 很多学者都在寻求求解这类问题的有效方法, 如Maher对约束可满足问题的求解方法进行了综述[16], Hooker综述了将局部约束转化为全局约束的方法[17], Liu等[18]对基于群体的metaheuristic算法(population-based metaheuristics,PBMH)进行了数学化描述, 提出了PBMH算法的统一框架,阐述了统一框架与特定算法间的关系, 同时给出了基于统一框架设计高效PBMH算法的若干指导原则, 并将统一框架扩展到基于PBMH的混合算法(memetic algorithm,MA), 最后基于Markov链理论分析了统一框架所描述算法的渐进收敛性. 鉴于机群保障资源配置问题的约束高度非线性且种类繁多、逻辑关系复杂等特性, 本研究基于POEM优化计算平台[19]求解该问题.
POEM求解的基本机制为: 首先尽量用约束切削解空间. 每当切削(cutting)的过程终止时, 如果存在某个查询变量的值域并非单元集(即解尚未被确定), 分枝(branching)的求解机制将被启动. 分枝的方法是将一些变量的值域一分为二, 将问题变为对应两个子域的子问题. 因为对所有变量的值域的二次分割都是有限性的, 所以随着切削及分枝的推进,系统对各子问题必将找到解或证明无解. 在无解的情况下,系统将回溯到其它分枝求解. 基本算法框架图如图 1所示.
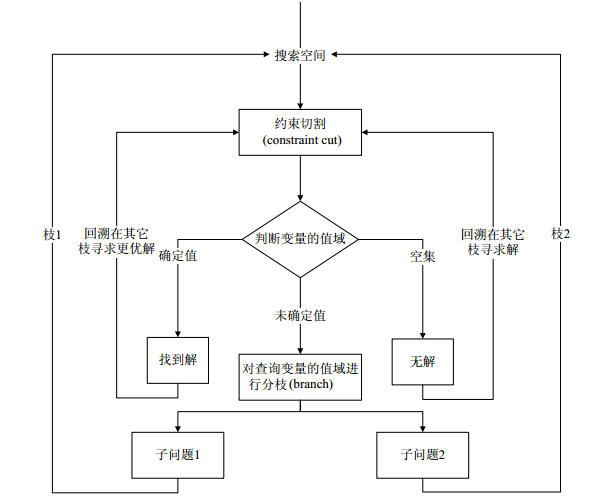 |
| 图 1 POEM求解机制 |
1)输入基础信息数据. 机群保障资源配置涉及的约束种类多,规模庞大, 数据量较大. 基础数据包括出动任务、机群保障的计划开始时间及结束时间、在分阶段滚动调度时资源占用情况、 保障业务工艺、各类资源数量、飞机在各保障位之间移动时间等.
2)给出模型的约束条件. 主要是可更新资源在每个时刻的供应量有限、消耗性资源消耗量不能超出其总量限制、 飞机保障工序不同需考虑移动时间约束、飞机前后继保障工序之间存在滞后时间的约束关系等. 具体参见公式(2)$\sim$(7).
3)制定搜索策略. 通过设计或者使用合适的启发式求解规则(如最小松弛度、最小遗憾度、贪婪性搜索等), 并在优化求解中引入问题信息,有助于高效求解调度问题. 为工序选择使用资源时考虑如下求解规则: ① 顺序性准则: 可开工时间最早的工序; ② 最小松弛度准则: 候选资源数最少的工序、可加工时间段最少的工序; ③ 尽量选可加工工序最少的资源; ④ 工序的平均候选资源数最少的资源; ⑤ 工序的时间松弛度最小的资源. 确定工序的开工时间时考虑如下求解规则: ① 顺序性准则: 最早开工工序、最早完工工序; ② 可选加工时间段最少的工序; ③ 尽量先加工加工时间长的工序; ④ 尽量先加工后继工序多的工序. 3.2 滚动调度
由于机群保障资源配置问题规模较大,为了高效地对该问题进行求解, 本文采用滚动调度思想, 将大规模、长周期的调度问题分解为若干小规模的单阶段的调度问题. 针对这些小规模问题,POEM可以在较短时间内获得满意解. 进而, 将小规模单阶段问题的解进行有机的串联, 形成原问题的一个较优的可行解.
滚动调度的基本思路为: 若干飞机在某一保障阶段的所有保障工序的调度视为原问题的一个子问题. 对该子问题,以单阶段最大完成时间最小化为优化目标. 在满足约束条件情况下,通过对待调度飞机的工保障序进行优化排序, 确定各保障作业的开始执行时间、占用的工位及接受保障服务的资源信息. 本阶段的调度结束之后, 将该阶段的状态信息作为下一个阶段调度的输入信息, 对下一阶段进行优化调度,直至所有的子问题求解完毕. 4 案例分析 4.1 典型任务模式案例
机群保障是指在满足各类约束下,对飞机进行各项保障作业, 从而提高飞机出动能力和保障执行任务效果. 通常飞机的保障作业流程可划分为五个大的阶段: 飞行前准备(m1)、起飞(m2)、回收(m3)、再次出动准备(mr1)、飞行后检查(m4). 如果一架飞机执行完m3之后执行m4,则该飞机执行的是单周期任务,反之, 如果紧接着执行mr1,则是多周期任务.
接下来以连续出动典型任务模式设计案例,在本案例中,需保障两组共8架飞机持续出动24架次, 每次出动4架次,以6个批次连续出动. m1共包含32道保障作业、m2共包含31道保障作业、m3共包含13道保障作业、m4共包含21道保障作业、 mr1共包含30道保障作业. 各批次的时序见表 1.
实验计算环境为 Intel Core(TM)i7 2.66GZ,内存为DDR3 1066Hz,4G, 操作系统为Windows 7(32-bit). 该任务耗时521.125秒. 4.2 结果分析
基于第2节建立的机群保障资源配置调度数学模型,利用POEM优化平台, 以每次出动4架飞机、6批次连续出动作为典型任务模式, 对模型和算法进行验证. 该案例中, 完成4架飞机6波次连续突击任务的保障时间(makespan)为15时26分43秒. 而根据原有机群保障系统的保障时间(makespan)为16个小时, 保障时间缩短了近33分钟. 这就表明基于POEM平台的机群保障资源配置建模与优化研究提高了机群的保障效率, 进而提高了作战能力. 4.2.1 资源约束满足分析
资源因素限制在机群保障过程中具有举足轻重的作用. 某些作业之间不存在前后继关系,但因资源能力约束而不能同时进行. 例如,某类保障资源只能同时进行一项保障任务, 如果两架飞机的任意两个保障作业,使用同一资源, 则其必定不能同时开始保障.
如表 2所示, 5号飞机(Product5)和6号飞机(Product6)在m1阶段的第1道保障作业(process01) 都用 到了编号为Device-08的资源, 则6号飞机只有等编号为5的飞机执行完作业后,才能使用该资源. 其中, t1和t2分别为保障作业开始和结束时间. 从表 2可以看出调度结果满足资源约束.
保障过程中,飞机要在不同保障站位之间移动以获取相应的保障服务. 飞机移动时,需要满足移动时间约束. 表 3给出了飞机从P10位置到P1位置的移动时间为30秒.
在表 4中, 7号飞机(Product7)的第2、3道保障作业(Process02和Process03)分别在P10、P1位置执行, 飞机在这两个保障站位之间的移动标准时间为30秒, 通过分析第2道保障作业的完工时间、第3道保障作业的开工时间, 可知优化结果满足飞机移动时间约束.
具有前后继约束的保障作业, 后道作业的开工时间必须在前道保障作业结束之后才能进行. 机群保障过程中,需要满足前后继约束, 表 5给出了某飞机保障作业间前后继关系. 其中, duration代表完成该作业所需要的时间,IdPrec为该作业的前继, IdSucc为该作业的后继.
从表 6飞机保障作业约束满足分析可以得出, 第3道保障作业(IdTask)的后继是第4道保障作业, 第4道保障作业的后继是第5、6道保障作业, 则优化结果需要满足第3道保障作业结束之后才能开始第4道作业, 第4道作业结束之后,才能执行第5、6道作业. 查看表 6所示的优化结果, 满足前后继约束.
机群保障资源配置优化问题面临超大规模性、长周期性等难点, 属于NP-hard难题,不能用精确算法求解, 须寻求该问题的有效近似算法. 为了克服上述难点对优化调度的影响, 本文引入滚动调度思想.
滚动调度面临两个主要的问题: 1)前一保障阶段飞机所占用的保障站位与后一阶段所占用保障站位之间的关系; 2)前一保障阶段完工时间和后一阶段开始时间的关系. 针对同一飞机的前后保障阶段,保障站位和保障时间均具有继承性. 如果前后两个保障阶段占用的保障站位相同, 则不需要考虑站位移动时间约束; 否则需要考虑飞机在两个保障站位之间的移动时间.
针对前后阶段时间的继承关系,假定前一组所有任务完成的时间作为下一组的最先开工时间. 由表 7可知: 8号飞机在m2阶段继承了m1阶段的保障站位与保障时间, 满足滚动调度约束.
本文对机群保障资源配置问题进行了深入分析, 厘清了保障过程中的各类约束条件,明确了机群保障资源配置的优化目标, 构造了机群保障资源配置的数学优化模型. 针对机群保障资源配置问题的大规模性与NP-hard性,采取滚动调度思想, 将大规模优化问题分解为若干子问题,进而提高了求解的效率. 同时, 借鉴业务规则,设计了简洁高效的启发式搜索策略. 最后以4架飞机6批次连续出动作为典型任务模式, 基于优化平台验证了模型和算法的有效性和高效性. 本研究从数学建模的角度对多波次多架飞机的保障全流程进行了建模. 同时本研究为机群保障资源配置优化问题提供了一种有效的解决思路. 本文只考虑确定性情况下的多机保障资源配置问题, 今后我们将考虑实际保障过程中存在不确定因素, 比如飞机战损、设备故障等. 此外, 高效的启发式算法和基于智能的优化算法也是我们下一步研究的重点.
致谢感谢中国科学院数学与系统科学研究院汪寿阳研究员、刘克研究员、刘波副研究员、清华大学金以慧教授、王凌教授、范文慧教授的讨论和帮助.
| [1] | 王凌, 刘波. 微粒群优化与调度算法[M]. 北京: 清华大学出版社, 2008.Wang Ling, Liu Bo. Particle swarm optimization and scheduling algorithms[M]. Beijing: Tsinghua University Press, 2008. |
| [2] | 李妍峰, 李军, 高自友. 动态规划启发式算法求解时变车辆调度问题[J]. 系统工程理论与实践, 2012, 32(8): 1712-1718.Li YanFeng, Li Jun, Gao Ziyou. Dynamic programming heuristics for solving time dependent vehicle routing problem. Systems Engineering——Theory & Practice. 2012, 32(8): 1712-1718. |
| [3] | 贺川, 邱涤珊, 朱晓敏, 等. 基于滚动优化策略的成像侦察卫星应急调度方法[J]. 系统工程理论与实践, 2013, 33(10): 2685-2694.He Chuan, Qiu Dishan, Zhu Xiaomin, et al. Emergency scheduling method for imaging reconnaissance staellites based on rolling horzion optimization strategy[J]. Systems Engineering——Theory & Practice, 2013, 33(10): 2685-2694. |
| [4] | 孙彬, 孙俊清, 陈秋双. 基于鲁棒反应式策略的泊位和岸桥联合调度[J]. 系统工程理论与实践, 2013, 33(4): 1076-1083.Sun Bin, Sun Junqing, Chen Qiushuang. Integrated scheduling for berth and quay cranes based on robust and reactive policy. Systems Engineering——Theory & Practice, 2013, 33(4): 1076-1083. |
| [5] | 王小乐, 黄宏斌, 邓苏, 等. 基于状态转移的UAV单机侦察任务调度策略研究[J]. 系统工程理论与实践, 2013, 33(8): 2141-2147.Wang Xiaole, Huang Hongbin, Deng Su, et al. Task scheduling policy based on state transition for single UAV reconnaissance[J]. Systems Engineering——Theory & Practice, 2013, 33(8): 2141-2147. |
| [6] | 罗江锋, 朱承, 刘忠, 等. 连续多目标来袭下的舰艇防空火力在线调度[J]. 系统工程理论与实践, 2014, 34(11): 2929-2937.Luo Jiangfeng, Zhu Cheng, Liu Zhong, et al. On-line schedule of the warship firepower when suffering from the attack of multiple continuous incoming objects[J]. Systems Engineering——Theory & Practice, 2014, 34(11): 2929-2937. |
| [7] | 姜维, 李一军. 天基预警调度方法研究[J]. 系统工程理论与实践, 2012, 32(9): 2065-2077.Jiang Wei, Li Yijun. The scheduling model and algorithm of space-based early warning[J]. Systems Engineering——Theory & Practice, 2012, 32(9): 2065-2077. |
| [8] | Kolisch R, Hartmann S. Experimental investigation of heuristics for resource-constrained project scheduling: An update[J]. European Journal of Operational Research, 2006, 174(1): 23-37. |
| [9] | Hartmann S. A self-adapting genetic algorithm for project scheduling under resource constraints[J]. Naval Research Logistics, 2002, 49(5): 433-448. |
| [10] | 冯强, 曾声奎, 康锐. 基于多主体的舰载机综合保障过程建模方法[J]. 系统工程与电子技术, 2010, 32(1): 211-216.Feng Qiang, Zeng Shengkui, Kang Rui. Multiagent-based modeling method for integrated logistic support of the carrier aircraft[J]. Systems Engineering and Electronics, 2010, 32(1): 211-216. |
| [11] | 林华, 占明锋, 周丰. 舰载机回收任务的优化调度算法及仿真[J]. 海军工程大学学报, 2008, 20(1): 50-54.Lin Hua, Zhan Mingfeng, Zhou Feng. Optimization schedule algorithm and simulation to recycle planes on carrier[J]. Journal of Naval University of Engineering, 2008, 20(1): 50-54. |
| [12] | 杨炳恒, 毕玉泉, 徐伟勤. 一种舰载机调运作业流程优化模型[J]. 舰船科学技术, 2011, 33(1): 118-121.Yang Bingheng, Bi Yuquan, Xu Weiqin. A model of aircraft handling workflow optimization[J]. Ship Science and Technology, 2011, 33(1): 118-121. |
| [13] | 方晨, 王凌. 资源约束项目调度研究综述[J]. 控制与决策, 2010, 25(5): 641-650.Fang Chen, Wang Ling. Survey on resource-constrained project scheduling[J]. Control and Decision, 2010, 25(5): 641-650. |
| [14] | Blazewicz J, Cellary W, Slowinski R, et al. Scheduling under resource constraints-deterministic models[M]. Basel: JC Baltzer, 1986. |
| [15] | Bartusch M, Möhring R H, Radermacher F J. Scheduling project networks with resource constraints and time windows[J]. Annals of Operations Research, 1988, 16(1): 199-240. |
| [16] | Maher M J. A logic programming view of CLP[C]// International Conference on Logic Programming, 1993: 737-753. |
| [17] | Hooker J N. Logic, optimization and constraint programming[J]. INFORMS Journal on Computing, 2002, 14(4): 295-321. |
| [18] | Liu B, Wang L, Liu Y, et al. A unified framework for population-based metaheuristics[J]. Annals of Operations Research, 2011, 186(1): 231-262. |
| [19] | Zhou J. Introduction to the constraint language NCL[J]. The Journal of Logic Programming, 2000, 45(1): 71-103. |








