0 引言
近年来,由于城市化进程以及人才流动的不断加速, 二手房交易市场异常火爆. 值得注意的是, 随着收入水平的不断提高以及人们对提高生活质量和水平的渴望, 在二手房交易中不仅存在买方只购买一套房子的情形, 而且常常出现两个关系紧密的家庭同时购买二手房的情形,例如, 为了调和照顾父母与工作、生活的时间冲突,需要考虑购买两套二手房, 一套用于自己居住,一套用于父母居住. 还常常出现一个家庭同时选择购买两套二手房的情形,例如, 一套用于居住,另外一套用于商用. 在这些有意愿购买两套房子的买方中, 不仅要求所购二手房要尽可能满足自己的购房基本需求, 还要求所购两套二手房的距离越近越好. 而且有的买方只选择一次性购买两套房, 有的买方则根据关于单套房子的满意度和两套房子组合满意度来决定购买数量. 为了能买到满意的二手房或以一个满意的价格出售二手房,买方或卖方总是求助于房产中介. 具体地,买方或卖方分别向中介提供需求或供给信息, 中介依据这些信息,试图达成一个令双方尽可能满意的匹配方案. 然而, 由于现实生活中二手房屋交易市场需求的不确定性以及买卖双方需求的复杂性, 获得一个使得双方都满意的匹配方案是困难的.因此,在二手房交易匹配问题中, 如何确定使得买卖双方的满意度最大的匹配方案, 已经成为当前交易匹配领域中重要的一个研究热点.
二手房交易匹配问题的研究起源于婚姻匹配问题的研究. 2012年诺贝尔经济学奖获得者, Shapley等最早针对婚姻匹配决策问题,考虑男女双方针对对方给出的强偏好序信息, 给出了寻求稳定匹配的G-S算法\,[1]; 另一位诺贝尔经济学奖获得者Roth等随后对G-S算法进行了扩展应用, 并提出双边匹配的市场设计实践理论[2];近年来, 随着二手房需求量的不断增加, 一些国内外学者开始关注二手房及其相关交易匹配问题的研究,并取得了一些成果, 如: Jung等考虑多个买家与多个卖家的情况,以买方与卖方互为值域, 以双方的属性是否得到满足为约束,将其转化为约束满足问题进行求解, 开发了求解器,并在房产中介网站中进行应用[3]; 樊治平等针对二手房交易匹配问题, 给出了基于公理设计的分析方法[4];张振华等研究了二手房交易匹配问题, 给出了基于理想点的分析方法[5];蒋忠中等针对二手房交易匹配问题, 考虑了买卖双方的模糊需求信息,构建了以买卖双方交易匹配度最大和交易数量最大为目标的优化模型[6];蒋忠中等研究了电子中介中具有数量折扣的多属性商品交易匹配问题, 构建了以最大化买卖双方加权匹配度为目标的优化模型[7]; Kwang等直接连接每一个可能进行交易的买家与卖家, 按属性满足程度对该连接进行评价,并按评价值大小进行匹配[8]; Ragone等运用模糊描述逻辑及数据日志对买卖双方提出的模糊信息进行描述, 实现了一个买家与多个卖家商品交易的优化匹配[9]; Yang 等对商品交易匹配问题进行了研究, 并给出了基于CBR的系统架构方法[10]; Tankuya等研究了一对多的交易匹配问题, 并给出基于惩罚占优理念的稳定双边匹配算法\,[11]; Ohta等考虑了不确定环境下的双边交易匹配问题, 并提出了连续稳定算法[12]; Joshi 等研究了电子交易市场中的匹配问题, 给出了基于妥协匹配的分析方法[13].
以上成果的取得,虽然丰富了解决二手房交易匹配问题的理论和方法, 但从已有研究成果来看, 对于二手房及其相关交易匹配问题的研究还比较单一, 即大多单纯考虑买方和卖方买卖一套二手房, 主要采用优化建模技术和递归算法,分别从匹配方案的满意性和稳定性的角度求解交易匹配问题. 而对于二手房组合交易匹配问题的研究所见甚少. 为解决上述问题, 本文设计了基于匹配满意度的扩展H-R算法. 1 问题描述
在现实的二手房组合交易匹配决策过程中, 买方和卖方在中介提供的交易平台上分别提出购买二手房的请求和出售二手房的请求, 并分别提供相应的需求信息. 中介作为决策主体, 同时考虑买方和卖方的利益, 根据买方和卖方提供的需求信息,确定匹配方案并分别推荐给买方和卖方. 在考虑的二手房组合交易匹配问题中,设由$n$ 个买方构成的买方集合为$B=\{B_1,B_2,\cdots,B_n\}$,其中 $B_j$为第$j$个买方,$j=1,2,\cdots,n$; 由$m$个卖方构成的卖方集合为$S=\{S_1,S_2,\cdots,S_m\}$,其中 $S_i$为第$i$个卖方,$i=1,2,\cdots,m$. 设$m$个交易的二手房集合为$H=\{H_1,H_2,\cdots,H_m\}$,其中 $H_i$为卖方$S_i$出售的二手房,评价二手房的$k$ 个属性构成的集合为$C=\{C_1,C_2,\cdots,C_k\}$,其中 $C_l$为第$l$个属性,$l=1,2,\cdots,k$; 评价二手房的属性可以为房屋价格、面积、小区物业管理等等, 中介一般通过调研的方法,并考虑自身的实际需求,确定具体的评价属性. 买方$B_j$给出的属性权重向量$W^j=(w_1^j,w_2^j,\cdots,w_k^j)$, 其中$w_l^j$表示买方$B_j$ 对属性$C_l$ 重要程度的描述, $\sum\nolimits_{l=1}^k{w_l^j=1}$,$0\le w_l^j\le1$. 需要指出的是, 买方$B_j$既可直接给出$w_l^j$的数值, 也可提供属性重要程度的语言描述或者两两属性重要性比较等信息, 中介随后采用AHP等方法来确定$w_l^j$.
根据当前二手房交易市场的需求特点,本文考虑如下三种需求类型的买方:
1) 买方只购买一套二手房,没有购买两套二手房的意愿,为方便叙述, 记此种类型的买方集合为$B^1$;
2) 买方只购买两套二手房,对于一套二手房不予考虑, 记此种类型的买方集合为$B^2$;
3) 买方或者购买两套二手房,或者购买一套二手房, 购买的数量主要取决于买方关于单套二手房或 二手房组合的满意度大小. 如果买方关于单套二手房的满意度更高,则买方购买一套二手房, 否则购买两套. 记此种类型的买方集合为$B^3$,其中$B^1\cup B^2\cup B^3=B$,$B^1\cap B^2=B^1\cap B^3=B^2\cap B^3=\emptyset$.
记$E=(e_{jl})_{n\times k}$为买方$B_j$对二手房的期望水平矩阵, 其中$e_{jl}$为买方$B_j$对二手房的属性$C_l$给出的期望水平. 记$R=(r_{il})_{m\times k}$为卖方$S_i$对二手房$H_i$的评价矩阵, 其中$r_{il}$为卖方$S_i$对二手房$H_i$的属性$C_l$给出的评价值.
设$D=(d_{ig})_{n\times k}$为二手房的距离矩阵, 其中$d_{ig}$表示二手房$H_i$与$H_g$的距离,$d_{ig}>0$, $i,g=1,2,\cdots,m$. 如果买方有购买两套房子的意愿,通常给出关于所购二手房之间的距离的期望. 设$\beta_j$为买方$B_j$关于两套二手房之间距离的期望值,$\beta_j>0$, $ B_j\in B^2 \cup B^3$.
基于上面的描述,本文根据买方对二手房属性的期望水平矩阵$E$和$\beta _j$、二手房属性的评价矩阵$R$ 以及二手房的距离矩阵$D$,通过某种匹配算法, 获得买方和卖方的匹配方案, 使得买卖双方对二手房组合交易的匹配满意度最大. 2 二手房组合交易匹配相关概念分析
下面首先给出二手房组合交易匹配方案的数学表述.
定义1 二手房组合交易匹配$\mu$定义为映射$\mu: S\cup B \rightarrow S\cup B$. 对于$\forall S_i \in S $,$\forall B_j\in B $,$\mu$满足如下条件:
1) $\mu(S_i )\subseteq B\cup \{ S_i \}$,若$\mu(S_i)=S_i$, 则说明卖方$S_i$没能将二手房$H_i$出售出去;
2) $\mu(B_j)\subseteq S\cup \{ B_j\}$,若$\mu(B_j)=B_j$, 则说明买方$B_j$没能购买到二手房;
3) 若$\mu(S_i)=B_j$,$\mu(B_j)=S_i$, 此时称$(S_i,B_j)$为根据匹配$\mu$确定的一个匹配对;
4) 对于$ B_j\in B$,若$\mu(S_i)=B_j$,则$\mu(S_i)\ne B_k$,$k\ne j$;
5) 对于$ B_j\in B^1$,若$\mu(B_j)=S_i$,则$\mu(B_j)\ne S_l$,$i\ne l$;
6) 对于$ B_j\in B^2$,若$\mu(B_j)=\{S_i,S_l\}$,则$\mu(B_j)\ne S_v$,$v\ne i\ne l$;
7) 对于$ B_j\in B^3$,若$\mu(B_j)=\{S_i,S_l\}$,则$\mu(B_j)\ne S_v$,$v\ne i$,$v \ne l$;
根据二手房组合交易匹配$\mu$所有匹配对的集合称为匹配方案.
为了获得一个好的匹配方案,考虑卖方和买方对匹配对象的满意度是一个非常重要的因素,它将直接影响整个匹配的 最终质量和效率. 本文考虑的买方的匹配满意度是指二手房满足买方期望水平的满意程度,买方的满意度越大,其购 买的热情和决心就越大. 而卖方的匹配满意度则是通过交易价格优于其关于二手房价格评价值的程度衡量,卖方的满意 度越大,其出售动机越强烈. 此外,一个好的匹配方案还应该是稳定的,所谓稳定匹配方案是指匹配方案中形成 匹配对的任意买方或卖方,除当前匹配对象以外,无法找到新的匹配对象,使得该买方或卖方与新匹配对象的满意 程度同时超过对各自现有匹配对象的满意程度[14]. 可见,匹配方案的稳定性与买卖双方的满意度密切相关.
设$a_{ig}^j$买方$B_j$对于二手房组合$(H_i,H_g)$的满意度, $H_i,H_g\in H$,$a_{ig}^j=a_{gi}^j$,特别地, 当买方只购买一套二手房时, 买方$B_j$对于二手房$H_i$的满意度可以表示为买方对于二手房组合$(H_i,H_i)$的满意度$a_{ii}^j$; 设$\eta _{ij}$表示卖方$S_i$对其与买方$B_j$的交易价格$p_{ij}$的满意度. 设卖方或买方与自身匹配的满意度为0.
为了方便叙述,设$\mu(B_j)=\{S_i,S_g\}$,$S_i,S_g\in S$,若$ B_j\in B^1$,则$ i=g $; 若$ B_j\in B^2$,则$ i\ne g$; 若$ B_j\in B^3$, 则$ i$和$ g$可以相等,可以不等.
根据匹配满意度,下面给出组合交易匹配的稳定匹配方案的数学定义.
定义2 对于二手房组合交易匹配$\mu: S\cup B \rightarrow S\cup B$确定的匹配方案,对$\forall S_i,S_g,S_l,S_p,S_v\in S $, $\forall B_j,B_k$,$B_u\in B $,其中$\mu(S_i)=B_j$, $\mu(S_v)=B_u$,$\mu(B_j)=\{S_i,S_g\}$. 若任意匹配对$(S_i,B_j)$ 和$(S_v,B_u)$ 不满足以下条件: 1) $\eta _{ik}\ge \eta _{ij}$,$\eta _{vk}\ge \eta _{vu}$且$a_{iv}^k\ge a_{lp}^k$, $\mu(B_k)=\{S_l,S_p\}$,(若$ B_k\in B^1$,则$ v=i $; 若$ B_k\in B^2$,则$ v\ne i $; 若$ B_k\in B^3$,则$ v$ 和$ i$可以相等, 可以不等); 2) $\eta _{ik}\ge \eta _{ij}$,$\eta _{vk}\ge \eta _{vu}$且$a_{iv}^k>0$,$\mu(B_k)=B_k$,(若$ B_k\in B^1$,则$ v=i $; 若$ B_k\in B^2$,则$ v\ne i $; 若$ B_k\in B^3$,则$ v$和$ i$可以相等,可以不等); 3) $a_{pl}^j\ge a_{ig}^j$,$\eta _{pj}>0$, $\eta _{lj}>0$,$\mu(S_p)=S_p$,$\mu(S_l)=S_l$; 4) $\eta _{ij},\eta _{gj},\eta _{vu},a_{lp}^k,a_{ig}^j\le 0$, 则称该匹配方案为稳定匹配方案.
通常地,一个稳定匹配方案应该是个体理性、不浪费和公平的. 依据文献[15]中关于一对一匹配中个体理性、不浪费、公平的定义,下面分别给出个体理性、不浪费、公平二手房组合交易匹配的定义.
定义3 对于二手房组合交易匹配$\mu: S\cup B \rightarrow S\cup B$确定的匹配方案,对$\forall S_i,S_g\in S $,$\forall B_j\in B $,其中$\mu(S_i)=B_j$,$\mu(B_j)=\{S_i,S_g\}$,若任意匹配对 $(S_i,B_j)$ 和$(S_g,B_j)$均满足$\eta _{ij},\eta _{gj},a_{ig}^j>0$, 则称该匹配方案为个体理性匹配方案.
定义4 对于二手房组合交易匹配$\mu: S\cup B \rightarrow S\cup B$确定的匹配方案,对$\forall S_i$,$S_g$,$S_v\in S $, $\forall B_k,B_j,B_u\in B $,其中$\mu(S_i)=B_j$,$\mu(S_v)=B_u$, $\mu(B_j)=\{S_i,S_g\}$,若任意匹配对$(S_i,B_j)$ 和$(S_v,B_u)$满足如下条件: 1) $\eta _{ik}\ge \eta _{ij}$,$\eta _{vk}\ge \eta _{vu}$但$\mu(B_k)\ne B_k$或$a_{iv}^k \le 0$,$S_v\in S$; 2) $a_{pl}^j\ge a_{ig}^j$,但$\mu(S_p)\ne S_p$,$\mu(S_l)\ne S_l$,或者$\eta _{pj}\le 0$或$\eta _{pj}\le 0$,$S_p,S_l\in S$, 则称该匹配方案为不浪费匹配方案.
在不浪费匹配方案中,虽然买方或卖方可能有更偏爱的匹配对象,但对方或者已经与其它的匹配对象形成了匹配对, 或者对该买方或卖方不满意.
定义5 对于二手房组合交易匹配$\mu: S\cup B \rightarrow S\cup B$确定的匹配方案,$\forall S_i,S_g,S_l,S_p\in S $,$\forall B_j,B_k\in B $,其中$\mu(S_i)=B_j$,$\mu(B_j)=\{S_i,S_g\}$, $\mu(B_k)=\{S_l,S_p\}$(若$ B_k\in B^1$,则$l=p\ne i,g$; $ B_k\in B^2$,则$l\ne p\ne i,g$; 若$ B_k\in B^3$,则$l,p\ne i,g$). 若$(S_i,B_j)$满足以下两个条件: 1) 如果$\eta _{ik} \ge \eta _{ij}$, 则$a_{lp}^k\ge a_{iv}^k$ (若$ B_k\in B^1$,则$ i=v $;若$ B_k\in B^2$,则$ i\ne v$,$v=1,2,\cdots,m$;若$ B_k\in B^3$, 则$v=1,2,\cdots,m$); 2) 对于$\forall S_v,S_q\in S $,$ B_u,B_r\in B $,满足$\mu(S_v)=B_u$,$\mu(S_q)=B_r$,如果$a_{qv}^j\ge a_{ig}^j$,则$\eta _{qr} \ge \eta _{qj}$,$\eta _{vu} \ge \eta _{vj}$ (若$ B_j\in B^1$,则$ q=v $; 若$ B_j\in B^2$,则$ q\ne v$; 若$ B_k\in B^3$,则$ q=v $ 或$ q\ne v$ 均可),则称该匹配方案为 公平匹配方案.
从定义5来看,公平匹配方案具有两方面的含义: 第一,由条件1)可知, 二手房越被买方满意,越有竞争力,才能出售给期望价格更高的买方. 条件1)中$\eta _{ik} \ge \eta _{ij}$表示$S_i$对交易价格$p_{ik}$的满意度超过交易价格$p_{ij}$,说明买方$B_k$的期望价格高于买方$B_j$, 即$p_{ik}>p_{ij}$. 而 $a_{lp}^k\ge a_{iv}^k$表示买方$B_k$对当前二手房组合$(H_l,H_p)$的满意度超过二手房$H_i$或包含二手房$H_i$ 的任意组合的满意度,说明买方$B_k$不会选择购买二手房$H_i$. 第二, 由条件2)可知,买方给出的期望价格越高,越有竞争力, 才可能购买到满意的二手房. 条件2)中$a_{qv}^j\ge a_{ig}^j$表示买方$B_j$对二手房组合$(H_q,H_v)$的满意度超过$(H_i,H_g)$. 而$\eta _{qr} \ge \eta _{qj}$ 和$\eta _{vu} \ge \eta _{vj}$分别表示卖方$S_q$和$S_v$对交易价格$p_{qr}$和$p_{vu}$的满意度超过$p_{qj}$和$p_{vj}$, 说明买方$B_r$和$B_u$的期望价格高于买方$B_j$.
公平匹配方案可以有效避免买方和卖方的投机操作行为,即买方不会由于故意给出较低的期望价格而 获得更好的二手房; 同时卖方不会由于故意提升关于二手房的估价而获得更高的交易价格.
关于稳定匹配与个体理性匹配、不浪费匹配和公平匹配之间的关系,可通过如下定理进行证明.
定理1 对于二手房组合交易匹配$\mu: S\cup B \rightarrow S\cup B$确定的匹配方案,若$\mu$是稳定匹配方案, 则$\mu$必是个体理性匹配方案、不浪费匹配方案和公平匹配方案.
证明 首先,证明$\mu$是个体理性匹配. 从稳定匹配的定义来看, 若一匹配方案$\mu$ 为稳定匹配方案,则根据定义2中的条件4, 对于$\mu(B_j)=\{S_i,S_g\}$,满足$\eta _{ij}>0$ 和$a_{ig}^j>0$, 显然,根据定义3,$\mu$为个体理性匹配方案.
然后,采用反证法证明$\mu$是不浪费匹配. 假设$\mu$是浪费匹配, 不妨设$\mu(B_j)=\{S_i,S_g\}$,$\mu(S_v)=B_u$,一方面,假设$\eta _{ij} \ge \eta _{ik}$,$\eta _{vk} \ge \eta _{vu}$时, 满足$\mu(B_k)=B_k$且$a_{iv}^k>0$同时成立,显然满足定义2中的条件2; 另一方面,假设$a_{pc}^{j} \ge a_{ig}^{j}$时,满足$\mu(S_p)=S_p$, $\mu(S_l)=S_l$,$\eta _{pj}>0$,$\eta _{lj}>0$, 显然满足定义2中的条件3; 综上,与$\mu$是稳定匹配方案矛盾, 进而$\mu$是不浪费匹配方案.
进一步地,仍采用反证法证明$\mu$是公平匹配方案. 假设$\mu$是不公平匹配,不妨设$\mu(S_i)=B_j$. 根据定义5,一方面, 存在$\exists B_K\in B$ 时,使得$\mu(B_k)=\{S_l,S_p\}$,当$\eta _{ik} \ge \eta _{ij}$ 和$\eta _{vk} \ge \eta _{uv}$ 时, 均有$a_{iv}^k\ge a_{lp}^k$成立,显然满足定义2中的条件1, 与$\mu$为稳定匹配矛盾. 另一方面,$\exists S_v,S_q\in B$,$\exists B_u,B_r\in B$,$\mu(S_v)=B_u$,$\mu(S_q)=B_r$,当$a_{qv}^j\ge a_{ig}^j$ 时,使得$\eta _{qj}>\eta _{qr}$,$\eta _{vj}>\eta _{vu}$,显然满足定义2 中的条件1,与$\mu$为稳定匹配矛盾. 由此可见, $\mu$为公平匹配方案.
下面给出帕累托二手房组合交易匹配的定义.
定义6 对于任意的匹配方案$\mu$和$\mu '$, 如果满足如下两个条件,则称匹配$\mu$帕累托占优于匹配$\mu '$:
1) 对于$\forall S_i,S_l\in S$,设$\mu(S_i)=B_j$,$\mu '(S_i)=B_k$, $ B_j,B_k\in B $,$S_i$在$\mu$中的匹配对象均不劣于在$\mu '$中的匹配对象,即$\eta _{ij} \ge \eta _{ik}$; 同时至少存在一个卖方$S_l$,$\mu(S_l)=B_p$,$\mu '(S_l)=B_q$, $B_p,B_q\in B$,$S_l$在$\mu$ 中的匹配对象优于在$\mu '$中的匹配对象,即$\eta _{lp}>\eta _{lq}$;
2) 对于$\forall B_j\in B$,$\mu(B_j)=\{S_i,S_g\}$,$\mu '(B_j)=\{S_v,S_t\}$,$S_i,S_g,S_v,S_t\in S$, $B_j$在$\mu$中的匹配对象均不劣于在$\mu '$中的匹配对象, 即$a_{ig}^j\ge a_{vt}^j$; 同时至少存在一个买方$B_k$,$B_k\in B$, 设$\mu(B_k)=\{S_p,S_l\}$,$\mu '(B_k)=\{S_e,S_r\}$, $S_p,S_l,S_e,S_r\in S$,满足$B_k$在$\mu$ 中的匹配对象优于在$\mu '$中的匹配对象,即$a_{pl}^k > a_{er}^k$.
特别地,如果匹配方案$\mu$帕累托占优于其他所有可能的匹配方案, 则$\mu$称为帕累托最优匹配方案; 如果没有其他匹配方案帕累托占优于匹配方案$\mu$,则称$\mu$为 帕累托有效匹配方案. 3 匹配决策分析方法
基于以上分析,下面给出多需求类型的二手房组合交易匹配决策方法. 具体地,为了使得买卖双 方获得尽可能满意且稳定的匹配方案,首先,给出了买方和卖方匹配满意度的计算方法. 然后,在考虑 匹配方案稳定性的基础上,设计基于匹配满意度的扩展H-R算法. 通过运行扩展H-R算法,可以获得一个 最优的二手房组合交易匹配方案. 3.1 买方和卖方的匹配满意度计算方法
本文考虑买方关于属性$C_l$给出两种形式的期望: 硬约束和软约束. 其中硬约束是指买方要求二手房的某属性值必须符合其所提出的期望水平; 软约束分为三种:效益型、成本型和区间型, 效益型和成本型软约束分别要求二手房的某属性值在其期望水平的基础上越大越好和越小越好, 而区间型软约束要求二手房的某属性值在其期望水平的范围之内.
为了计算买卖双方关于交易价格的满意度, 需要首先确定买卖双方之间的交易价格. 为了公平起见,本文将交易价格定义为买方期望价格和卖方期望价格的中间值, 即若属性$C_l$表示交易价格, 则确定买方$B_j$与卖方$S_i$之间的交易价格$p_{ij}$为
| $p_{ij}=(r_{il}+e_{jl})/2,i=1,2,\cdots,m,j=1,2,\cdots,n$ | (1) |
设$a_{ijl}$为买方$B_j$对二手房$H_i$的属性$C_l$的满意度. 考虑买方给出不同类型的约束,$a_{ijl}$可由如下方法给出.
当属性$C_l$为交易价格时,则$a_{ijl}$的计算公式为
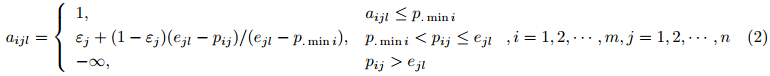
当属性$C_l$不表示交易价格时,则考虑如下形式的四种属性约束:
1) 当买方$B_j$关于属性$C_l$提出硬约束,则$a_{ijl}$的计算公式为
| $a_{ijl} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {r_{il} \in e_{jl} } \hfill \\ { - \infty ,} \hfill & {r_{il} \notin e_{jl} } \hfill \\ \end{array}} \right.,i=1,2,\cdots,m,j=1,2,\cdots,n$ | (3) |
2) 当买方$B_j$关于属性$C_l$提出效益型约束,则$a_{ijl}$的计算公式为
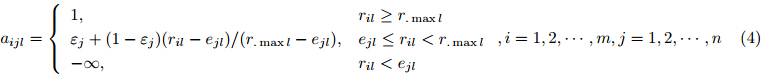
3) 当买方$B_j$关于属性$C_l$提出成本型约束,则$a_{ijl}$的计算公式为
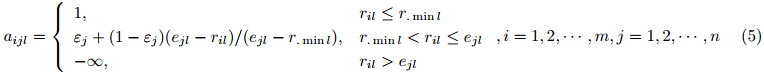
4) 当买方$B_j$关于属性$C_l$提出区间型约束,则$a_{ijl}$的计算公式为
| $a_{ijl} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {e_{jl}^L \le r_{il} \le e_{jl}^U } \hfill \\ { - \infty ,} \hfill & {r_{il} < e_{jl}^Lmbox{or}\ r_{il} > e_{jl}^U } \hfill \\ \end{array}} \right.,i=1,2,\cdots,m,j=1,2,\cdots,n$ | (6) |
之后,再考虑有购买两套二手房意愿买方的距离需求. 设$\lambda _{ig}^j$表示买方$B_j$关于二手房组合$(H_i,H_g)$距离的满意度, 这里$B_j \in B^2 \cup B^3$. $\lambda _{ig}^j$可由下式给出:
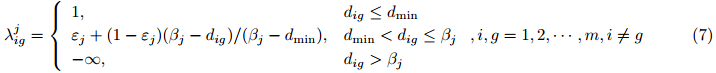
进一步地, 根据上述所得到的买方关于单套二手房多属性的满意度以及关于二手房组合距离的满意度,并考虑不同需求类型的买方, 可分别计算不同需求类型买方的匹配满意度.
情形1 若买方$B_j \in B^1$,则买方$B_j$关于二手房$H_i$多属性信息的满意度$a_{ii}^j$由下式给出:
| $a_{ii}^j = \sum\limits_{l = 1}^k {w_l^j a_{ijl} },i,g=1,2,\cdots,m$ | (8) |
情形2 若买方$B_j \in B^2$,那么, 买方$B_j$关于二手房$(H_i,H_g)$ 的满意度$a_{ig}^j$包括$B_j$关于二手房$H_i$和$H_g$ 多属性信息的满意度和关于二手房组合 $(H_i,H_g)$距离的满意度, 具体地,$a_{ig}^j$可由下式得到
| $a_{ig}^j = \omega _1^j {{(a_{ii}^j + a_{gg}^j )} / 2} + (1 - \omega _1^j )\lambda _{ig}^j,i,g=1,2,\cdots,m,i\ne g$ | (1) |
情形3 若买方$B_j \in B^3$, 由于买方$B_j$既可以接受一套二手房,也可以接受两套二手房, 主要取决于两者满意度的大小. 因此,由公式(8)和(9), 可分别计算买方$B_j$关于$(H_i,H_i )$$(i=1,2,\cdots,m)$和$(H_i,H_g)$$(i \ne g,i,g = 1,2,\cdots ,m)$的满意度 $a_{ii}^j$和 $a_{ig}^j$.
类似地,对于卖方而言, 交易时只需要考虑买方给出的价格是否在可接受的范围内. 因此,设$\xi _i $表示交易价格刚好为卖方价格时的满意度,$0<\xi_i\le 1$, 卖方的匹配满意度$\eta_{ij}$可由下式给出:
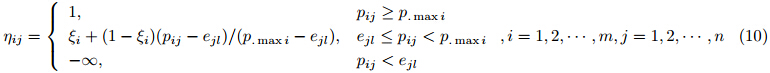
在现实的二手房组合交易匹配决策问题中, 卖方的匹配目标在于最大化其关于交易价格的满意度, 买方的匹配目标在于最大化其关于购买的二手房的满意度, 中介则总是希望他的组合收益可以最大. 由于买方和卖方的满意度越高, 形成交易的成功率就越高,中介的组合收益也就越大. 因此, 中介确定的匹配方案将尽可能贴近于卖方和买方的需求, 即买方关于二手房组合的满意度和卖方关于交易价格的满意度越大, 相应的匹配方案越优.
为尽可能达成卖方、中介和买方的目标, 求得买方和卖方获得尽可能满意且稳定的结果, 本文根据经典H-R算法的思想[15, 16], 给出基于匹配满意度的扩展H-R算法. 该算法的核心思想为: 买方首先向其最满意的二手房组合提出购买意向, 每个卖方在收到多个购买意向后, 选择出当前购买意向列表中最满意的买方, 如果符合其需求并且当前没有匹配对象, 则卖方暂时接受列表中最满意的买方;如果当前有匹配对象, 但卖方关于列表中最满意的买方的满意度更大, 则卖方暂时接受列表中最满意的买方. 对于买方来说, 只有当其提出意向的一个卖方接受或两个卖方同时接受他,才能达成匹配, 否则, 买方将当前最满意的二手房组合从符合其需求的集合中删除,生成新的符合买方需求的集合. 被拒绝的买方重复上述操作, 直到找到匹配对象或再也无法找到符合需求的二手房为止.
下面给出具体的算法,首先对算法中使用的变量进行描述.
设迭代变量$t$,$P_{B_j }^{(t)}$和$P_{S_i }^{(t)}$分别为在第$t$次迭代时符合买方$B_j$需求和符合卖方$S_i$需求的二手房组合集合; 设$U_{S_i }^{(t)}$为第$t$ 次迭代时卖方$S_l$收到购买意向集合, $B^{(t)}$和$V^{(t)}$为第$t$次迭代时未匹配的买方集合和已经匹配的买方集合, $V^{(t)} \cup B^{(t)} = B$,$ V^{(t)} \cap B^{(t)} = \emptyset$; $(H_{(t)1},H_{(t)2})$为满足$a_{(t)1(t)2}^j=\max \{a_{ig}^j ,(H_i,H_g)\in P_{B_j }^{(t)}\}$时的二手房组合,若$B_j \in B^1$,则$(t)1=(t)2$; 若$B_j \in B^2$,则$(t)1\ne (t)2$; 若$B_j \in B^3$,则$(t)1$和$(t)2$可以相等,可以不等,$(t)1,(t)2 \in \{1,2,\cdots,m\}$. 设$\mu ^{(t)}$为第$t$次迭代时得到的匹配方案.
关于扩展H-R算法描述如下:
Step 1 迭代变量初始化. 令迭代变量$t=1$,$U_{S_i }^{(1)}=\emptyset$,$V^{(1)}=\emptyset$,$B^{(1)}=B$,$P_{B_j }^{(1)}=\emptyset$,$P_{S_i}^{(1)}=\emptyset$,$\mu ^{(1)}(S_i)=\emptyset$,$\mu ^{(1)}(B_j)=\emptyset$;
Step 2 筛选符合$S_i$和$B_j$需求的集合. 若$a_{ii}^j>0$且$ B_j \in B^1 \cup B^3$,则$ P_{B_j }^{(t)} = P_{B_j }^{(t)} \cup \{ (H_i ,H_i )\}$; 若$ a_{ig}^j>0$,$i\ne g$且$ B_j \in B^2 \cup B^3$,则$ P_{B_j }^{(t)} = P_{B_j }^{(t)} \cup \{ (H_i ,H_g )\}$; 若$\eta_{ij}>0$,则$ P_{S_i }^{(t)} = P_{S_i }^{(t)} \cup \{ B_j \}$;
Step 3 买方$B_j$向最满意的二手房组合提出购买意向. 对于买方$ B_j \in B^{(t)}$,计算 $a_{(t)1(t)2}^j=\max \{a_{ig}^j,\\ (H_i,H_g)\in P_{B_j }^{(t)}\}$,令$U_{S_{(t)1} }^{(t)}=U_{S_{(t)1} }^{(t)} \cup \{ B_j \} $,$U_{S_{(t)2} }^{(t)}=U_{S_{(t)2} }^{(t)} \cup \{ B_j \} $. 当$ \mu ^{(t)} (S_{(t)1} ) =\emptyset$且$ \mu ^{(t)} (S_{(t)2} ) =\emptyset$时,则转Step 4; 当$\mu ^{(t)} (S_{(t)1} ) = B_{(t)y1} $ 且$\mu ^{(t)} (S_{(t)2} ) = B_{(t)y2} $时,$(t)y1,(t)y2 \in \{1,2,\cdots ,n\}$,则转Step 5; 当$\mu ^{(t)} (S_{(t)1} )= B_{(t)y1} $ 且$\mu ^{(t)}(S_{(t)2})=\emptyset$ 时,$(t)y1\in \{1,2,\cdots ,n\}$,则转Step 6; 当$\mu ^{(t)} (S_{(t)1} ) = \emptyset$ 且$\mu ^{(t)} (S_{(t)2} ) = B_{(t)y2} $时,$(t)y2 \in \{1,2,\cdots ,n\}$,则转Step 7;
Step 4 卖方$S_{(t)1}$和$S_{(t)2}$判断是否接受买方$B_j$. 当$ B_j\in P_{S_{^{(t)1}}}^{(t)}$,$ B_j\in P_{S_{^{(t)2}}}^{(t)}$,并且$\eta_{(t)1j}=\max\{\eta_{ij},B_j \in U_{S_{(t)1}}^{(t)}\}$, $\eta_{(t)2j}=\max\{\eta_{ij},B_j \in U_{S_{(t)2}}^{(t)}\}$,则$ \mu ^{(t)} (B_j)=\{S_{(t)1},S_{(t)2}\}$,$V^{(t)}=V^{(t)}\cup \{ B_j\}$,$B^{(t)}=B^{(t)}-\{ B_j\}$,转Step 8;
Step 5 卖方$S_{(t)1}$和$S_{(t)2}$判断是否放弃原匹配对象. 当$\eta_{(t)1j}=\max \{\eta _{ij},B_j\in U_{S_{(t)1}}^{(t)}\}$, $\eta_{(t)2j}=\max \{\eta _{ij},B_j\in U_{S_{(t)2}}^{(t)}\}$, 且满足$ \eta _{(t)1j}> \eta _{(t)1(t)y1}$和$ \eta _{(t)2j}> \eta _{(t)1(t)y2}$时,则$ \mu ^{(t)}(B_j )=\{ S_{(t)1},S_{(t)2}\}$, $V^{(t)}=V^{(t)}\cup \{ B_j\}$,$B^{(t)}=B^{(t)}-\{ B_j\}$, $P_{B_{(t)y1}}^{(t)}=P_{B_{(t)y1}}^{(t)}-\{(H_{(t)1},H_i),i\in \{1,2,\cdots,m\}\}$,$P_{B_{(t)y2} }^{(t)}=P_{B_{(t)y2} }^{(t)}-\{(H_{(t)2},H_i),i\in \{1,2,\cdots ,m\}\}$, $B^{(t)}=B^{(t)}\cup \{B_{(t)y1},B_{(t)y2}\}$,转Step 8;
Step 6 卖方$S_{(t)1}$判断是否放弃原匹配对象, $S_{(t)2}$判断是否接受买方$B_j$. 当$\eta_{(t)1j}=\max \{\eta _{ij},B_j\in U_{S_{(t)1}}^{(t)}\}$,$\eta_{(t)2j}=\max \{\eta _{ij},B_j\in U_{S_{(t)2}}^{(t)}\}$,且满足$ \eta _{(t)1j}> \eta _{(t)1(t)y1}$和$B_j\in P_{S_{^{(t)2}}}^{(t)}$时,则$ \mu ^{(t)}(B_j )=\{ S_{(t)1},S_{(t)2}\}$,$V^{(t)}=V^{(t)}\cup \{ B_j\}$,$B^{(t)}=B^{(t)}-\{ B_j\}$, $P_{B_{(t)y1}}^{(t)}=P_{B_{(t)y1}}^{(t)}-\{(H_{(t)1},H_i),i\in \{1,2,\cdots,m\}\}$,$B^{(t)}=B^{(t)}\cup \{B_{(t)y1}\}$,转Step 8;
Step 7 $S_{(t)1}$判断是否接受买方$B_j$,卖方$S_{(t)2}$判断是否放弃原匹配对象. 当$\eta_{(t)1j}=\max \{\eta _{ij},B_j\in U_{S_{(t)1}}^{(t)}\}$, $\eta_{(t)2j}=\max \{\eta _{ij},B_j\in U_{S_{(t)2}}^{(t)}\}$, 且满足$ \eta _{(t)2j}> \eta _{(t)2(t)y2}$和$B_j\in P_{S_{^{(t)1}}}^{(t)}$时,则$ \mu ^{(t)}(B_j )=\{ S_{(t)1},S_{(t)2}\}$,$V^{(t)}=V^{(t)}\cup \{ B_j\}$, $B^{(t)}=B^{(t)}-\{ B_j\}$, $P_{B_{(t)y2}}^{(t)}=P_{B_{(t)y2}}^{(t)}-\{(H_{(t)2},H_i),i\in \{1,2,\cdots,m\}\}$,$B^{(t)}=B^{(t)}\cup \{B_{(t)y2}\}$,转Step 8;
Step 8 判定算法是否终止. 令$t=t+1$, 若$B^{(t)}\ne\emptyset$且$ \forall B_j\in B^{(t)}$,$ P_{B_j }^{(t)}\ne\emptyset$,转Step 3; 否则转Step 9;
Step 9 结束程序.
定理2 扩展H-R算法获得的匹配方案为稳定匹配方案.
证明 设$\mu$为所获得的匹配,不妨设$\forall S_i,S_g,S_l,S_p,S_v\in S$,$B_j,B_k,B_u\in B$, 有$\mu(B_k)=\{S_l,S_p\}$,$\mu(B_j)=\{S_i,S_g\}$,$\mu(S_v)=B_u$. 采用反证法,现假设$\mu$为不稳定匹配,则存在如下情形之一: 1) $\eta_{ik} \ge \eta_{ij}$,$\eta_{vk}\ge \eta_{vu}$且$a_{iv}^k\ge a_{lp}^k$; 2) $\eta_{gk}\ge \eta_{gj}$,$\eta_{vk}\ge \eta_{vu}$且$a_{iv}^k\ge a_{lp}^k$; 3) $a_{ig}^k\ge a_{lp}^k$, $\eta_{ik} \ge \eta_{ij}$且$\eta_{gk}\ge \eta_{gj}$.
不失一般性,下面以3)为例进行证明.
根据扩展H-R算法的思想, 买方$B_k$总是先向更满意的二手房组合提出购买意向,若$a_{ig}^k\ge a_{lp}^k$,则买方$B_k$先对二手房组合$(H_i,H_g)$ 提出购买意向. 而$\mu(B_j)\ne \{S_i,S_g\}$,说明卖方$S_i$ 和$S_g$中至少一个拒绝了买方. 不失一般性,不妨设$S_i$在第$t$ 次迭代时拒绝$B_k$,并且设$\mu^{(t)}(S_i )=B_q$,则$\eta_{iq}> \eta_{ij}$.
但是,$\mu(S_i )=B_j\ne B_q$,说明卖方$S_i$一定拒绝了买方$B_q$, 并且选择了更为满意的买方$B_j$,即$\eta_{ij}> \eta_{iq}> \eta_{ik}$. 显然,与已知条件$\eta_{ik}\ge \eta_{ij}$矛盾, 进而所获得的匹配$\mu$为稳定匹配.
定理3 扩展H-R算法获得的匹配方案为稳定匹配方案.
证明 设$\mu$为所获得的匹配. 采用反证法, 现假设$\mu$不是帕累托有效匹配, 则一定存在某一匹配$\mu'$帕累托占优于匹配$\mu$,即$ \exists B_j \in B$,$S_i,S_v,S_g,S_t\in S$,$\mu(B_j)=\{S_i,S_g\}$, $\mu'(B_j)=\{S_v,S_t\}$,满足$a_{vt}^j>a_{ig}^j>0$.可见,采用扩展H-R算法时, 买方一定先向二手房组合$(H_v,H_t)$提出购买意向, 并且卖方$S_v$和$S_t$中至少一个拒绝了买方$B_j$, 否则$\mu(B_j)=\{S_v,S_t\}$.
另一方面,只有出现更满意的买方时, 卖方$S_v$和$S_t$才会拒绝买方$B_j$,不妨设$\mu(S_v)=B_l$ 和$\mu(S_t)=B_k$,满足$\eta_{vl}> \eta_{vj}$ 和$\eta_{ik}> \eta_{ij}$,显然卖方$S_v$和$S_t$认为匹配$\mu$优于$\mu'$. 这与$\mu'$帕累托占优于匹配$\mu$矛盾.
需要指出的是, 经典的H-R算法主要针对匹配双方给出个体偏好序信息的情形[15, 16], 而本文提出的扩展H-R算法不仅可以解决匹配双方给出个体偏好序信息的双边匹配决策问题, 还可以解决匹配双方给出组合偏好序信息或满意度信息的双边匹配决策问题. 4 实例分析
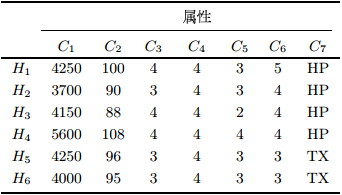
现有某市A房产中介机构收集了6个卖方的出售请求和4个买方的购买请求. 在二手房交易中,主要考虑6个属性: 房屋价格($C_1$,单位:元/平方米), 建筑面积($C_2$,单位:平方米),物业管理($C_3$),小区环境($C_4$), 交通便利性($C_5$),周边配套设施($C_6$)和位置($C_7$,单位:区). 对于定性属性$C_3$,$C_4$, $C_5$和$C_6$,卖方采用1-5标度进行评价,其中"1"表示很差, "5"表示很好.
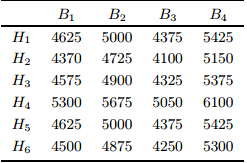
假设6个卖方提交卖房请求,并且提供给A中介的二手房评价信息, 如表 1所示. 6个卖方$S_1$,$S_2$,$S_3$,$S_4$, $S_5$和$S_6$给出的交易价格刚好为其期望价格时的满意度, 即当交易价格分别为4250,3700,4150,5600,4250 和4000时的满意度, $\xi_1=0.4$,$\xi_2=0.55$,$\xi_3=0.5$,$\xi_4=0.45$,$\xi_5 =0.5$和$\xi_6=0.4$.
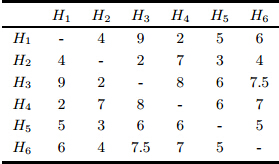
令'-'表示不存在,A中介经过实地考察和测量, 获得待出售的6套二手房之间的距离信息,如表 2所示.
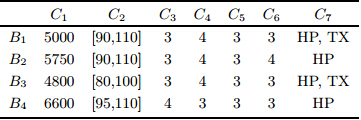
4个买方$B_1$,$B_2$,$B_3$和$B_4$关于二手房的多属性需求信息, 如表 3所示.
买方对于所购的二手房距离要求,如表 4所示.
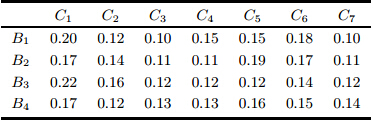
4个买方$B_1$,$B_2$, $B_3$和$B_4$给出的刚好满足其期望水平时的满意度,即$\varepsilon _1=0.4$,$\varepsilon _2=0.45$,$\varepsilon_3 =0.55$和$\varepsilon_4=0.5$. 假设中介根据买方关于属性重要程度的比较信息,采用AHP方法, 确定4个买方的权重信息,如表 5所示.
A中介根据买方的需求数量,确定了买方的需求类型,即$ B_3 ,B_4\in B^1$,$ B_1\in B^2$,$ B_2\in B^3$. 下面根据第2节中给出的匹配决策分析方法,确定最优匹配方案.
首先,根据式(1),确定买方和卖方之间的交易价格,如表 6所示.
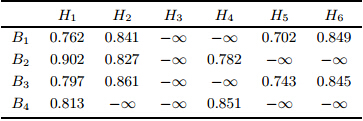
然后,根据式(2)$\sim$(6),计算买方关于二手房多属性信息的满意度, 如表 7所示.
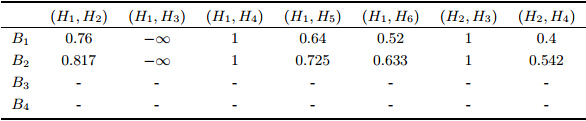
再根据式(7),计算买方关于二手房组合距离的满意度, 如表 8所示.
假设$B_1$和$B_2$给出的多属性信息满意度的权重分别为$\omega _1^1=0.5$和$\omega_1^2=0.4$. 根据式(8)$\sim$(9), 计算买方关于二手房组合的综合满意度,如表 9所示.
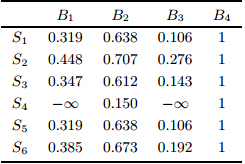
之后,根据式(10),计算卖方关于交易价格的匹配满意度,如表 10所示.
最后,根据表 9和表 10,采用扩展的H-R算法,得到最优的匹配方案,具体的迭代过程如表 11所示.
即最终的二手房组合交易匹配结果为$B_1\leftrightarrow \{ S_2 ,S_5 \}$,$B_2\leftrightarrow S_1$,${B_3\leftrightarrow S_6}$和${B_4\leftrightarrow S_4}$. 5 结束语
本文针对二手房组合交易匹配决策问题, 提出了二手房组合交易匹配方案的定义, 提出了个体理性、不浪费、公平、稳定、帕累托占优和帕累托有效匹配方案的定义, 给出了扩展的H-R算法. 该算法根据经典H-R算法的思想, 在综合考虑买方和卖方的匹配满意度基础上, 求得稳定且帕累托有效的匹配方案. 与已有研究成果相比, 所给出的二手房组合交易匹配决策方法, 弥补了已有单纯考虑单套二手房交易匹配问题的不足, 方便了买方更灵活的表达需求信息, 也使得关于二手房交易匹配问题的研究更贴近现实需求, 进一步完善了二手房交易匹配问题的理论和方法. 值得指出的是, 本文提出的二手房组合交易匹配决策方法, 还可以解决其他交易匹配决策问题, 如:二手房与车库组合交易匹配决策问题、雇主与家政人员组合交易匹配问题等等, 提供了理论和方法上的借鉴.
| [1] | Gale D, Shapley L. College admissions and the stability of marriage[J]. American Mathematical Monthly, 1962, 69(1): 9-15. |
| [2] | Roth A E. Common and conflicting interests in two-sided matching markets[J]. European Economic Review, 1985, 27(1): 75-96. |
| [3] | Jung J J, Jo G S. Brokerage between buyer and seller agents using constraint satisfaction problem models[J]. Decision Support Systems, 2000, 28(4): 293-304. |
| [4] | 樊治平, 陈希. 电子中介中基于公理设计的多属性交易匹配研究[J]. 管理科学, 2009, 22(3): 83-88. Fan Zhiping, Chen Xi. Research on multi-attribute trade matching problem in electronic broker based on axiomatic design[J]. Journal of Management Science, 2009, 22(3): 83-88. |
| [5] | 张振华, 汪定伟. 电子中介在旧房市场中的交易模型研究[J]. 系统仿真学报, 2006, 2: 492-495. Zhang Zhenhua, Wang Dingwei. Research on trading model of electronic broker in second-hand apartment market[J]. Journal of System Simulation, 2006, 2: 492-495. |
| [6] | 蒋忠中, 樊治平, 汪定伟. 电子中介中具有模糊信息且需求不可分的多属性商品交易匹配问题[J]. 系统工程理论与实践, 2011, 31(12): 2355-2366. Jiang Zhongzhong, Fan Zhiping, Wang Dingwei. Trade matching for multi-attribute exchanges with fuzzy information and indivisible demand in E-brokerage[J]. Systems Engineering —— Theory & Practice, 2011, 31(12): 2355-2366. |
| [7] | 蒋忠中, 袁媛, 樊治平. 电子中介中具有数量折扣的多属性商品交易匹配问题研究[J]. 中国管理科学, 2010, 18(6): 122-130. Jiang Zhongzhong, Yuan Yuan, Fan Zhiping. Multi-attribute trade matching with quantity discount in electronic brokerage[J]. Chinese Journal of Management Science, 2010, 18(6): 122-130. |
| [8] | Kwang M S, Raymond C. A brokering protocol for agent-based e-commerce[J]. IEEE Transactions on Systems, Man, and Cybernetics —— Part C, 2000, 30(4): 474-484. |
| [9] | Ragone A, Straceiab U, Noiaa T D, et al. Fuzzy matchmaking in e-marketplaces of peer entities using Datalog[J]. Fuzzy Sets and Systems, 2009, 160(2): 251-268. |
| [10] | Yang J, Jiao Y B. Case-based reasoning for semi-automatic trade matching for electronic commerce broker[J]. Service Systems and Service Management, 2012: 528-532. |
| [11] | Tankuya M. Punishment-dominance condition on stable two-sided matching algorithms[J]. Kyoto Joint Global Center of Excellence Program, 2012, 18: 1-15. |
| [12] | Ohta N, Iwamoto K, Kuwabara K. Changeable two-sided matching for changing environment[C]// IEEE 11th International Conference on Cognitive Informatics & Cognitive Computing, 2012: 24-32. |
| [13] | Joshi M, Bhavsar V C, Boley H. Compromise matching in P2P e-marketplaces: Concept, algorithm and use case[M]. Multi-disciplinary Trends in Artificial Intelligence. New York: Springer Berlin Heidelberg, 2011: 384-394. |
| [14] | 魏立佳. 弱偏好序下的最优单边匹配算法设计[J]. 系统工程理论与实践, 2011, 31(9): 1687-1695. Wei Lijia. Optimal mechanism design of weak preference orders one-sided matching[J]. Systems Engineering —— Theory & Practice, 2011, 31(9): 1687-1695. |
| [15] | Balinski M, Sönmez T. A tale of two mechanisms: Student placement[J]. Journal of Economic Theory, 1999, 84(1): 73-94. |
| [16] | Roth A E. On the allocation of residents to rural hospitals: A general property of two-sided matching markets[J]. Econometrica: Journal of the Econometric Society, 1986, 54(2): 425-427. |