2. 东南大学 经济管理学院, 南京 210096;
3. 中国科学院 虚拟经济与数据科学研究中心, 北京 100190
2. School of Economics and Management, Southeast University, Nanjing 210096, China;
3. Research Center on Fictitious Economy and Data Science, ChineseAcademy of Sciences, Beijing 100190, China
0 引言
随着供应链的规模日益扩大,供应链结构愈来愈复杂. 科技的发展、经济全球化的进一步深入 以及市场需求异质化,供应链中的企业所面临的风险和不确定性也越来越多. 例如雪糕、冷饮、冬装、空调等季节性产品的需求受气温、天气等诸多因素影响,导致需求不确 定. 因设备故障、供应流程的中断、运输过程中的破损以及由于自然灾难、恐怖活动和政治动荡等因素而导致供应不确定[1]. 在竞争日益激烈的商业环境中,企 业需要时刻衡量和应对不确定性风险. 因此,将需求风险和供应风险考虑到运营决策中显得非常必要.
文献[2]指出报童模型的决策是选择一个合适的订货量以实现期望利润最大化或者期望成本最小化. 此时,决策者被假定是风险中性的. 然而,现实中的许多决策者的最优决策与采用期望效用最大化准则或期望成本最小化准则所获得的最优决策不一致. 此种现象被称为报童问题中的决策偏差. 存在决策偏差的主要 原因是管理者的风险态度不仅仅是风险中性的,管理者还有其他不同的风险偏好[3]. 例如,在20世纪80年代早期,克莱斯勒汽车公司比它的竞争对手通用汽车公司和福特汽车公司拥有更多的库存[4],这就是文 献[3]所说的缺货避免行为. 在主要的风险偏好中,决策者普遍具有损失厌恶的偏好. 损失厌恶指人们在对同样大小数值进行比较时,相对于收益往往更加看重损失. 这一理论已经被经济学、金融学、市场营销学和组织行为学的大量文献所支持[5]. 对于大多数研究需求不确定性的文献而言,文献[3, 6, 7, 8, 9]引入损失厌恶偏好的研究较为新颖. 对短销售期和长生产期的服装产品的管理,供应风险对零售商而言是重要的影响因素. 因此,当决策者具有损失厌恶偏好时,考虑供应风险和需求风险下的最优决策具有非常重要的价值. 同时,研究这种情况下的决策偏差以及降低供应风险的策略显得非常重要.
本文研究与现有文献的关系体现在以下三个方面:1)具有风险厌恶成员的供应链决策; 2)需求不确定性和供应不确定性对决策的影响; 3)提前支付策略降低供应风险.
文献[6]最早将损失厌恶引入报童模型,发现损失厌恶报童的最优订货量小于风险中性报童的最优 订货量. 文献[9]研究面临市场需求信息更新时具有两次订货选择的损失厌恶零售商的订货决策. 文献[10]研究具有较长提前期的损失厌恶的按单生产企业面临的定制件采购决策问题. 文献[11]研究由一个风险中性制造商和一个损失厌恶零售商组成的供应链的协调问题. 文献[12]研究当损失厌恶零售商面临批发价格合同和具有现货采购机会时的零部件采购问题. 文献[13]将文献[7]的研究扩 展到考虑产品替代的情况. 文献[14]研究一个具有损失厌恶偏好的零售商面临供应不确定和需求不确定情况的订货决策. 上述文献中,考虑损失厌恶的文献多为针对供应链协调的研究. 在研究报童模型的相关文献中,较少考虑供应不确定性,而同时考虑需求不确定性和供应不确定性的文献则很少见.
文献[15]研究零售商同时进行营销决策和库存决策时,供应不确定性对零售商效益的影响. 研究发现降低供应不确定性的方差有利于提高企业利润. 文献[16]研究具有供应不确定和买家竞争的情况下的 供应商多元化策略. 文献[17]研究下游企业如何通过激励机制来激励上游供应商进行投资以降低产能波动,并将其与可靠供应但价格更高的情况进行了比较. 文献[18]分别研究在内部生产和外部采 购的情况下,供应不确定性对同时进行价格决策和订货量决策的零售商的影响. 文献[19]则研究同 时面临需求和供应不确定的决策者的提前销售策略. 文献[20]提出可以通过收益共享契约来实现供应和需求不确定环境下的供应链协调. 以上研究供应不确定性的文献中,部分文献没有考虑需求不确 定性,或者没有考虑决策者的损失厌恶风险态度.
文献[21]将商业信用对供应链的协调作用与数量折扣契约对供应链的协调作用进行对比,发现商业信用在一定条件下比 数量折扣契约更优. 文献[22]则分析由多个零售商和单个供应商组成的供应链协调中商业信用所发挥的作用. 文献[23]分析不对称信息条件下商业信用契约的设计,发现随着零售商的风险厌恶程度 的增大,商业信用的激励作用会减弱. 还有其它很多文献将商业信用作为协调激励机制改善供应链 的运营效率,这些文献主要是考虑基于延期支付的商业信用. 而只有极少数文献,如文献[24, 25, 26, 27] 考虑基于提前支付的商业信用. 仅有的考虑提前支付的商业信用文献中,提前支付量都没有作为决策变量进行研究. 此外,这些研究也没有考虑需求不确定性和决策者的风险偏好.
本文其余部分内容如下: 第1节主要对基础模型进行简单描述,并给出零售商的最优订货决策. 第2节研究提前支付策略降低供应风险及零售商的最优决策. 第3节给出论文的结论及未来进一步研究的方向. 1 基础模型描述
考虑由一个零售商和一个供应商组成的单周期两阶段供应链. 供应商的产品供应比例不确定,假定实际到货率为$Y(0 考虑零售商具有损失厌恶的风险偏好,我们采用文献[28]中的损失厌恶效用函数. 则具有损失厌恶风险偏好的零售商的效用函数$U(\Pi(Q; Y,D)) $可以表述为
令$EU(Q; \lambda)$对$Q$求导,可以证明最优订货量的存在性和唯一性,得到如下定理.
定理1 损失厌恶型零售商的期望效用函数$EU(Q; \lambda)$是关于$Q$ 的凹函数,且问题(5)存在唯一最优解,该最优解满足一阶条件$(w_0-w_1)\overline{y}-(w_0-s)\int_0^1yF(Qy){}G(y)-\lambda(w_1-s)\int_0^1yF(d(Q; y)){ d}G(y)=0$.
证明 对$EU(Q; \lambda)$求关于$Q$的一阶导数,得
$\frac{{}EU(Q; \lambda)}{{}Q}=(w_0-w_1)\overline{y}-(w_0-s)\int_0^1yF(Qy){}G(y)-\lambda(w_1-s)\int_0^1yF(d(Q; y)){ d}G(y). $ $(w_0-w_1)\overline{y}-(w_0-s)\int_0^1yF(Q^*y){}G(y)-\lambda(w_1-s)\int_0^1yF(d(Q^*; y)){ d}G(y)=0. $ 为了降低供应风险,零售商希望上游供应商能够采取措施降低供应不确定性. 但是,由于供应商在研发、原 材料采购、生产和运营等方面均需支出较多的资金,没有动力、更没有富余资金去改善供应可靠性. 假设零售商为了更好地满足市场需求,降低因供应不确定造成的损失,有比较大的动力去帮助供应商降低供应不确 定性. 零售商具有非常雄厚的资金实力和充足的现金流. 因此,假定零售商可以提前支付部分或全部货款给 供应商,让供应商用于改善供应可靠性. 另一方面,供应商为了维持与下游企业的良好合作关系,也愿意在有较充足资金的情况下投入资金改善供应可靠性,为下游企业提供更可靠的供应和更高质量的服务.
2.1 模型描述
假定提前支付比例为$\beta$,即零售商在收到货物之前就支付$\beta w_1Q$的货款给供应商. 供应商收到 提前支付的货款后,相当于得到了等量的无息贷款,并将之用于改善供应可靠性. 参考文献[26, 29],假定通过提前支付改善供应可靠性后的供应率满足$Y_{\beta}=(1-\beta)Y+\beta EY $. 因此,改善后供应比例$Y_\beta$的均值为$EY_{\beta}=EY=\mu$,方差为$VAR(Y_\beta)=E(Y_\beta)^2-(EY_\beta)^2=(1-\beta)^2VAR(Y)=(1-\beta)^2\sigma^2 $. 与改善前相比,改善后供应率均值不变且方差随$\beta$值增大而减小. 由此说明,零售商提前支付的比例越高,供应商 供应比例的均值不变,而供应比例的方差却越小. 即随机供应比例在均值不变情况下波动程度变小,从而供应 可靠性增加. 当$\beta=0$时,$Y_{\beta}=Y $; 当$\beta=1 $时,$Y_{\beta}=EY$.
对于零售商而言,提前支付货款降低了供应的不确定性而增加了收益,但同时也负担了一部分的资金成本. 假设零售商的无风险投资利率为$r$,参考文献[30]采用连续复利计息法,则在提前期$T$内的利息为$c={e}^{rT}-1 $. 需要说明的是,由于提前支付比例以全部到货为基础,因此有可能实际到达货物的货款小于提前支付的货 款,即$w_1QY_{\beta}<\beta w_1Q$. 在此情况下,供应商须在货物送达后立即将多余的款项还给零售商. 而由于零售商资金实力雄厚,为了保持与供应商的良好关系,多余的利息将不予追取. 其它假定条件不变,则零售商的利润函数$\Pi(Q,\beta)$可以表述为
令$\Pi_1(Q,\beta)=0$和$\Pi_2(Q,\beta)=0$,可得
$$d_1(Q,\beta)=\frac{(w_1-s)QY_{\beta}+\beta Qw_1c}{p-s}$$
和
$$d_2(Q,\beta)=\frac{-(w_0-w_1)QY_{\beta}+\beta Qw_1c}{p-w_0}. $$
与第1节中模型一致,零售商仍然具有损失厌恶的风险偏好. 因此,在有提前支付的情况下,零售商的期望效用函数可以表述为
定理2 提前支付下损失厌恶零售商的期望效用函数$EU(Q,\beta)$是关于订货量$Q$和提前支付比例$\beta$的联合凹函数,且问题(8)存在唯一最优解$(Q^*,\beta^*)$.
证明 根据假定市场需求$D$服从区间$[a,b]$上的均匀分布,可以进行化简得到
从上述公式可以得知,它是关于$Q$和$\beta$的联合凸函数. 利润函数中的其余项为关于$Q$或$\beta$的一次 函数. 因此,可以得知零售商的利润函数是关于$Q$和$\beta$的联合凹函数. 根据凹函数的定义,对于$E\Pi(Q,\beta)$上的任意两个点$(Q_1,\beta_1)$和$(Q_2,\beta_2)$,可以得到
$$E\Pi\bigg(\frac{Q_1+Q_2}{2},\frac{\beta_1+\beta_2}{2}\bigg)\ge \frac{E\Pi(Q_1,\beta_1)+E\Pi(Q_2,\beta_2)}{2}. $$
又由于${(\cdot)}^+=\max\{\cdot,0\} $是非减的凸函数,因此可以得到
以下通过分析给出$EU(Q,\beta)$关于$Q$和$\beta$的一阶导数方程组,将$\Psi(Q,\beta)$表达式进行化简得
在图 1中,上下两条虚线分别表示$QY_{\beta}$的下限$Q\beta \mu$(当$Y=0$时)和上限$Q(1-\beta+\beta \mu) $(当$Y=1$时). 三条直线$D=d_1(Q,\beta)=\frac{(w_1-s)QY_{\beta}+\beta Qw_1c}{p-s}$、$D=d_2(Q,\beta)=\frac{-(w_0-w_1)QY_{\beta}+\beta Qw_1c}{p-w_0}$与$D=QY_{\beta}$相 交于点 $(\frac{\beta Qw_1c}{p-w_1},\frac{\beta Qw_1c}{p-w_1})$. 在区域$R_1$,有$\Pi_1(Q,\beta)\le 0$; 在区域$R_2$,有$\Pi_2(Q,\beta)\le0$. 因此,区域$R_1$和$R_2$实际上取决于点$(\frac{\beta Qw_1c}{p-w_1},\frac{\beta Qw_1c}{p-w_1}) $的位置. 如果点$(\frac{\beta Qw_1c}{p-w_1},\frac{\beta Qw_1c}{p-w_1})$在$Q\beta \mu$和$Q(1-\beta+\beta \mu)$之间,则$D\le QY_{\beta}$和$D>$\noindent $QY_{\beta}$上各有一部分区域,使得零售商的利润小于零,此时有$\frac{w_1c}{p-w_1}>\mu$. 但在实际中这种情况发生的可能性非常小,因为在正常的利率水平以及正常的供应比例平均值情况下,只有当零售商的单位产品利 润率(即$\frac{p-w_1}{w_1}$)非常低的时候,此不等式才成立. 而在本节的模型中,我们假定零售商的资金实力非常雄厚,这在一定程度上说明单位产品利润率较高,且所有未满足的需求均需要通过紧急订货来满 足,这说明缺货成本高,同时也说明单位产品的利润较高. 因此,我们在假定$\frac{w_1c}{p-w_1}<\mu $时,此时点$(\frac{\beta Qw_1c}{p-w_1},\frac{\beta Qw_1c}{p-w_1}) $在$Q\beta \mu$下方. 综上所述,我们得到
$$\Psi(Q,\beta)=\int_0^1\int_0^{d_1(Q,\beta)}\Pi_1(Q,\beta){}F(x){ d}G(y) . $$
我们在本节中对模型的参数进行分析,研究其对决策者的决策和期望效用的影响.
2.2.1 损失厌恶的影响
考虑零售商损失厌恶程度分别为$\lambda$和$\lambda'$,其他假定不变,令$(Q_\lambda^*,\beta_\lambda^*)$为零售商损失厌恶程度为$\lambda$时的最优决策,$(Q_{\lambda'}^*,\beta_{\lambda'}^*)$为零售商损失厌恶程度为$\lambda'$时的最优决策. 通过分析零售商损失厌恶程度对最优决策的影响,得到如下性质.
性质1 1)最优订货量$Q^*$随着零售商的损失厌恶程度增加而减小; 2)如果$\frac{\partial \Psi(Q^*,\beta^*)}{\partial \beta}>0$,则最优提前支付比例$\beta^*$随着零售商的损失规避程度 增加而减小,反之则亦然.
证明 1)对于任意$\lambda <\lambda'$,有$$ \frac{\partial EU(Q^*_{\lambda},\beta^*_{\lambda}; \lambda')}{\partial Q}-\frac{\partial EU(Q^*_{\lambda},\beta^*_{\lambda}; \lambda)}{\partial Q}=(\lambda-\lambda')\frac{\partial \Psi(Q^*_{\lambda},\beta^*_{\lambda})}{\partial Q} . $$由式(11)得$$\frac{\partial \Psi(Q,\beta)}{\partial Q}=\int_0^1[(w_1-s)y_{\beta}+\beta w_1c] F(d_1(Q,\beta)){}G(y)>0,$$则$\frac{\partial \Psi(Q^*_{\lambda},\beta^*_{\lambda})}{\partial Q}>0$,因此$(\lambda-\lambda')\frac{\partial \Psi(Q^*_{\lambda},\beta^*_{\lambda})}{\partial Q}<0$,从而有$\frac{EU(Q^*_{\lambda},\beta^*_{\lambda}; \lambda')}{\partial Q}<0 $. 根据凹函数的特性,可以得知当损失厌恶程度$\lambda$增大时,最优订货量减小.
2)类似地有$\frac{\partial EU(Q^*_{\lambda},\beta^*_{\lambda}; \lambda')}{\partial \beta}-\frac{\partial EU(Q^*_{\lambda},\beta^*_{\lambda}; \lambda)}{\partial \beta}=(\lambda-\lambda')\frac{\partial \Psi(Q^*_{\lambda},\beta^*_{\lambda})}{\partial \beta}$. 当$\frac{\partial \Psi(Q^*_{\lambda},\beta^*_{\lambda})}{\partial \beta}>0$时,$\frac{\partial EU(Q^*_{\lambda},\beta^*_{\lambda}; \lambda')}{\partial \beta}<0$,根据凹函数的特性,此时最优提前支付比例随着损失厌恶程度的增大而减小. 反之则亦然. 证毕.
2. 2. 2 需求不确定性的影响
考虑随机市场需求为$D$和$D_1$,它们的概率分布函数分别为$F(\cdot)$和$F_1(\cdot)$. 其它假定不变,令$(Q_F^*,\beta_F^*)$为随机需求为$D$时的最优决策,$EU_F(Q_F^*,\beta_F^*)$为相应最优期望效用; $(Q_{F_1}^*,\beta_{F_1}^*)$为随机需求为$D_1$时的最优决策,$EU_{F_1}(Q_{F_1}^*,\beta_{F_1}^*)$ 为相应的最优期望效用. 本节将采用一阶随机占优和二阶随机占优的方法来比较需求风险对决策和效用的影响.
性质2 若随机需求$D$一阶随机占优于随机需求$D_1$时,则有1)最优期望效用增大,即 $EU_F(Q_{F}^*,\beta_{F}^*) \geq EU_{F_1}(Q_{F_1}^*,\beta_{F_1}^*)$; 2)最优订货量增大,即$Q_F^*\geq Q_{F_1}^*$; 3)若满足$(w_0-s)\int_0^1y_{\beta}[F_1(Qy_{\beta})-F(Qy_{\beta})]{}G(y)+\lambda\int_0^1[(w_1-s)y_{\beta}+\beta w_1c][F_1(d_1(Q,\beta))-$ 证明 根据文献[18]中定义可得: 若$D\succeq_{st}D_1$,则对于任意的$x$,$P\{D>x\}\geq P\{D_1>x\} $. 即,若随机需求$D$一阶随机占优于随机需求$D_1$时,则可得$F(x)\leq F_1(x)$.
1)由于$EU_F(Q,\beta)-EU_{F_1}(Q,\beta)=(w_0-s)\int_0^1\int_0^{QY_\beta}A{}x{ d}G(y)+\lambda(p-s)\int_0^1\int_0^{d_1(Q,\beta)}A{}x{ d}G(y)$,其中$A=(F_1(x)-F(x))$. 所以随机需求$D$一阶随机占优于随机需求$D_1$时,则由$F(x)\leq F_1(x)$得 $EU_F(Q,\beta)\geq EU_{F_1}(Q,\beta)$,进而可证$EU_F(Q_{F}^*,\beta_{F}^*) \geq EU_{F_1}(Q_{F_1}^*,\beta_{F_1}^*)$.
2)由随机需求$D$一阶随机占优于随机需求$D_1$,可以得到$F(Q^*_FY_\beta)\le F_1(Q^*_FY_\beta) $,并且$F(d_1(Q^*_F,\beta^*_F))\le F_1(d_1(Q^*_F,\beta^*_F))$,$F(d_2(Q^*_F,\beta^*_F))\le F_1(d_2(Q^*_F,\beta^*_F))$. 从而可以证明$\frac{\partial EU_F(Q_{F}^*,\beta_{F}^*)}{\partial Q}\geq \frac{\partial EU_{F_1}(Q_F^*,\beta_F^*)}{\partial Q}$,则可得$\frac{\partial EU_{F_1}(Q_F^*,\beta_F^*)}{\partial Q}\leq0$. 根据凹函数的特性即可得到$Q_F^*\geq Q_{F_1}^*$.
3)由于$\frac{\partial EU_F(Q^*_{F},\beta^*_{F})}{\partial \beta}-\frac{\partial EU_{F_1}(Q^*_F,\beta^*_F)}{\partial \beta}=(w_0-s)\int_0^1Q(\mu-y)[F_1(Qy_{\beta})-F(Qy_{\beta})]{}G(y)+\lambda\int_0^1[(w_1-s)(\mu-y)$ 性质2说明,在一阶随机占优条件下,需求越是随机大,最优订货量就越大,而相应的最优期望效用也越大. 这是因为,需求随机大的时候,零售商需要更多的库存来满足需求,从而订货量更大. 期望销售数量增加而增加了利润,进而增加了最优期望效用. 此外,市场需求一阶随机占优并不一定会使最优提前支付比例增大,也可能使其减小.
将一阶随机占优的条件放松至二阶随机占优时,可以得到如下性质.
性质3 若随机需求$D$二阶随机占优于随机需求$D_1$时,1)最优期望效用增大,即$EU_F(Q_F^*; \beta_F^*)\geq U_{F_1}(Q_{F_1}^*; \beta_{F_1}^*)$. 2)若$\lambda\int_0^1[(w_1-s)y_{\beta}+\beta w_1c][F_1(d_1(Q,\beta))-F(d_1(Q,\beta))]{ d}G(y)$满足,则零售商的最优订货量增大,即$Q^*_{F}> Q^*_{F_1}$; 否则有$Q^*_{F} 证明 根据文献[18]中定义可得: 若$D\succeq_{ssd}D_1$,则对于任意$t$,$\int_0^t(F_1(x)-F(x)){ d}x\ge 0 $. 即,随机需求$D$二阶随机占优于随机需求$D_1$时,则对于$t\in[0,+\infty)$,可得$\int_0^tF(x){ d}x\leq \int_0^tF_1(x){ d}x$.
1)$EU_F(Q,\beta)-EU_{F_1}(Q,\beta)=(w_0-s)\int_0^1\int_0^{QY_{\beta}}A{}x{ d}G(y)+\lambda(p-s)\int_0^1\int_0^{d_1(Q,\beta)}A{}x{ d}G(y)$,其中$A=(F_1(x)-F(x))$. 当随机需求$D$二阶随机占优于需求$D_1$时,则由$\int_0^tF(x){}x\leq \int_0^tF_1(x){ d}x$得$EU_F(Q,\beta)\geq EU_{F_1}(Q,\beta)$,进而可证明$EU_F(Q_{F}^*,\beta_{F}^*) \geq EU_{F_1}(Q_{F_1}^*,\beta_{F_1}^*)$.
2) $\frac{\partial EU_F(Q^*_{F},\beta^*_{F})}{\partial Q}-\frac{\partial EU_{F_1}(Q^*_F,\beta^*_F)}{\partial Q}$即等于性质3中第二条的判定条件,它既可能是正的也可能是负的,根据凹函数的特性,即可得到相应的结论.
3) $\frac{\partial EU_F(Q^*_{F},\beta^*_{F})}{\partial \beta}-\frac{\partial EU_{F_1}(Q^*_F,\beta^*_F)}{\partial \beta}$即等于性质3中第三条的判定条件,它既可能是正的也可能是负的,根据凹函数的特性,即可得到相应的结论. 证毕.
性质3说明,当市场需求二阶随机占优时,最优期望效用增大. 也就是说,需求风险降低导致最优期望效用增 大. 直观地理解,当需求分布的方差较小时,零售商的最优订货量和最优提前支付比例也会相应地减小. 但这一直观理解在有些情况下并不成立,正如性质3所示,需求风险降低时,最优订货量的变化是不确定的,可 能变大也可能变小. 同理,最优提前支付比例也可能变大或变小.
2. 2. 3 紧急订货价格的影响
紧急订货价格是影响最优决策和最优效用的重要因素. 通过模型分析可以很容易地发现,期望效用函数关于 紧急订货价格递减. 直观地理解,如果紧急订货价格比较高,零售商就会提高订货数量,以尽量避免或减少 紧急订货的数量. 以下性质也证实了我们的直观理解.
性质4 1)当紧急订货价格上升时,最优期望效用减小; 2)当紧急订货价格上升时,最优订货量增大; 3)当紧急订货价格上升时,最优提前支付比例增大.
证明 1)令$w_0'>w_0$,显然$\Psi(Q; \lambda)$不受$w_0$的影响,只需分析$w_0$对$\Pi(Q; Y; D)$的影 响. 当$D\le QY_{\beta}$时,则$\Pi(Q; Y; D)=\Pi_1(Q; Y,D)$不受$w_0$影响; 当 $D>QY_{\beta}$时,则$\Pi(Q; Y,D)=\Pi_2(Q; Y,D)$,显然$\Pi_2(Q; Y,D)$关于$w_0$递减. 由此可证期望效用 关于$w_0$递减.
2)由$$\frac{\partial EU(Q^*_{w_0},\beta^*_{w_0}; w_0)}{\partial Q}-\frac{\partial EU(Q^*_{w_0},\beta^*_{w_0}; w_0')}{\partial Q}=-(w_0'-w_0)\int_0^1y_{\beta}g(y)[1-F(Qy_{\beta})]{ d}y,$$令$w_0'>w_0$,则可得$$ \frac{\partial EU(Q^*_{w_0},\beta^*_{w_0}; w_0)}{\partial Q}-\frac{\partial EU(Q^*_{w_0},\beta^*_{w_0}; w_0')}{\partial Q}<0 ,$$因此有$\frac{\partial EU(Q^*_{w_0},\beta^*_{w_0}; w_0')}{\partial Q}>0 $. 根据凹函数的特性得$Q^*_{w'_0}>Q^*_{w_0}$.
3)由$$\frac{\partial EU(Q^*_{w_0},\beta^*_{w_0}; w_0)}{\partial \beta}-\frac{\partial EU(Q^*_{w_0},\beta^*_{w_0}; w_0')}{\partial \beta}=(w_0'-w_0)\int_0^1Q(\mu-y)F(Qy_{\beta}){ d}G(y) ,$$假定市场需求$D$服从区间$[a,b]$上的均匀分布,据此$\int_0^1Q(\mu-y)F(Qy_{\beta}){}G(y)=Q^2\frac{(\beta-1)\sigma^2}{b-a}\leq0 $. 令$w_0'>w_0$,则有$\frac{\partial EU(Q^*_{w_0},\beta^*_{w_0}; w_0')}{\partial \beta}>0$. 因此$w_0$增大时,$\beta^*$也增大. 证毕.
2. 3 提前支付策略分析
零售商通过提前支付来提高供应可靠性以降低供应风险,那么零售商的效用是否得到了提高是值得深入探讨的问题. 鉴于模型难以通过公式推导进行比较分析最优决策和最优效用,因此我们采用算例进行比较. 假定参数 如下: $p=10 $、$w_0=8 $、$w_1=4$、$s=2 $、$D\sim U(100,200)$、$Y\sim U(0,1)$、$\lambda=1 $. 令资金成本$r$变化,求出相应的最优订货量、最优提前支付比例和相应的最优效用,得到图 2、图 3和图 4.
图 2说明,随着资金成本的上升,零售商的最优提前支付比例随着资金成本的上升而降低. 直观地来看,当资金成本上升时,零售商进行提前支付所需要付出的额外成本变得越来越高,从而会减少提前支付比例. 如 果提前支付比例不作为决策变量时,我们可以很容易分析出最优订货量将随着资金成本的上升而增加. 而正如图 3所示,当零售商同时对订货量和提前支付比例进行决策时,资金成本的上升仍然导致了最优订货量的减小. 这是因为,资金成本对订货量有着两个不同方向 的影响,既增加了提前支付资金成本而导致订货量减小(提前支付以订货量为依据),又减小了提前支付 比例(如图 2所示)而导致供应可靠性降低,从而零售商会增加订货量. 但在本文模型背景下,前者的影响力明显地超过了后者的影响力,从而导致最优订货量的减小. 当资金成本到一定高度时,零售商就不再 进行提前支付,此时的订货量刚好等于第1节模型(即无提前支付的模型)中的最优订货量. 此外,图 4 说明最优期望效用也随着资金成本的增加而减小,当资金成本足够高时,零售商的最优期望效用刚好等于第1节模型中的最优效用. 由此可以得出,在资金成本相对较低时,通过提前支付,零售商的最优期望效用确实得到了改善.
3 结论与展望
在供应链日益复杂的今天,供应链企业不仅面临需求的不确定性,也面临供应的不确定性. 通过下游零售 企业的提前支付,供应商可以增强其供应的可靠性,降低供应链短缺的风险. 同时,零售商的偏好不仅仅 是风险中性,更可能是损失厌恶. 因而,在损失厌恶型零售商面临供应及需求不确定时,如何通过提前支付降低零售商的供应风险具有非常重要的作用. 本文在典型报童模型的基础上,在考虑需求不确定性、供应不确定性以及零售商具有损失厌恶风险偏好情况下,研究零售商通过提前支付改善供应可靠性的 决策问题. 结果表明,在需求服从均匀分布时存在最优解的订货量及提前支付比例. 本文同时还分析了零售商的损失厌恶程度、需求风险以及紧急订货价格对于最优解和相应的最优期望效用的影响. 通过数值算例分析,发现提前支付确实可以使零售商的最优效用得到改善. 然而,随着资金成本的上升,提前支付比例逐渐减 小,期望效用改善的程度逐渐减小. 本文在引入提前支付时仅考虑了提前支付对供应比例方差的影响而不考虑对均值的影响. 但在现实中,供应可靠性和提前支付的关系非常复杂. 提前支付并不只是影响方差,也 可能影响均值,对于两者的关系,需要深入地分析和研究. 此外,论文还可以扩展到研究提前支付商业信用如何影响到整个供应链绩效.
上式说明,当到货量大于需求时,即$D\le QY $时,零售商不需要进行紧急订货. 此时零售商的利润由销售收入$pD$、残值$s(QY-D)$和常规订货成本$w_1QY$三部分组成. 当到货量小于需求时,即$D> QY $ 时,则零售商需要进行紧急订货以满足缺货需求. 此时零售商的利润由销售收入$pD$、常规订货成本$w_1QY$和紧急订货成本$w_0(QY-D)$三部分组成. 当$D(Q; Y)=(w_1-s)QY/(p-s)$时,有$\Pi_1(Q; Y,D)\le 0$; 而当$\Pi_1(Q; Y,D)\le 0$时,$\Pi_2(Q; Y,D)>0$恒成立.
$\Pi(Q;Y,D)%=pD-w_1QY-w_2(D-QY)^++s(QY-D)^+\\
%&=&pD-w_1QY+w_2(QY-D)-(w_2-s)(QY-D)^+\\
=\left\{
\begin{array}{ll}
\Pi_1(Q;Y,D)=(p-s)D-(w_1-s)QY,& \hbox{if $D\le QY$}\\
\Pi_2(Q;Y,D)=(p-w_0)D+(w_0-w_1)QY,& \hbox{if $D>QY$}
\end{array}
\right.$
(1)
其中$\lambda>0$是损失厌恶系数,反映了决策者的损失厌恶程度. $\lambda$越大表示决策 者损失厌恶程度越大; 当$\lambda=0$时,零售商是风险中性的. $\pi_0 $是决策者目标利润,与文献[3, 9]一致,假定目标利润$\pi_0=0$,这表明零售商的决策目标是不亏损. 此时零售商的期望效用函数$EU(Q; \lambda) $可以表述为
U(Π(Q;Y,D)) = Π(Q;Y,D)−λ(π0−Π(Q;Y,D))+
(2)
EU(Q;λ)=E[Π(Q;Y,D)]−λE[−(Π(Q;Y,D)]+
(3)
其中,$E[\Pi(Q; Y,D)]=(p-w_0)\mu_d+(w_0-w_1)Q\mu-(w_0-s)\int_0^1\int_0^{Qy}F(x){}x{ d}G(y)$是零售商的 期望利润; $\lambda\Psi(Q; \lambda)=-\lambda(p-s)\int_0^1\int_0^{d(Q; Y)}{}x{ d}G(y) $是由于零售商的 损失厌恶态度而产生的负效用. 因此,该损失厌恶型零售商的决策是为问题(5)选择合适的订货量$Q$.
=E[Π(Q;Y,D)] +λΨ(Q;λ)
(4)
$\max\limits_{Q\ge 0}\ EU(Q;\lambda)$
(5)
$\Pi(Q,\beta)
%=(p-w_0)D+(w_0-w_1)QY+(w_0-w_2-c)q-(w_2-s)(QY-D)^+-(w_0-w_2)(QY+q-D)^+\\
=\left\{
\begin{array}{lll}
\Pi_1(Q,\beta)=(p-s)D-(w_1-s)QY_{\beta}-\beta Qw_1c,& \hbox{if $D\le QY_{\beta}$}\\
\Pi_2(Q,\beta)=(p-w_0)D+(w_0-w_1)QY_{\beta}-\beta Qw_1c,& \hbox{if
$D> QY_{\beta}$}
\end{array}
\right.$
(6)
其中$E\Pi(Q,\beta)=(p-w_0)\mu_d+(w_0-w_1)Q\mu-(w_0-s)\int_0^1\int_0^{QY_{\beta}}F(x){}x{ d}G(y)-\beta Qw_1c$ 是零售商的期望利润. $\lambda\Psi(Q,\beta)=-\lambda E(-\Pi(Q,\beta))^+$是由于零售商的损失厌恶 而产生的负效用. 因此,该损失厌恶零售商的决策就是为问题(8)选择合适的订货量$Q$和提前支付比例$\beta$.
$EU(Q,\beta)=E\Pi(Q,\beta)+\lambda\Psi(Q,\beta)$
(7)
为了简化分析,假定市场需求$D$服从区间$[a,b]$上的均匀分布. 此时,可以证明最优订货量和最优提前支付 比例的存在性和唯一性,得到如下定理.
$\max\limits_{Q\ge 0,1\ge \beta \ge 0}\ EU(Q,\beta)$
(8)
$\int_0^1\int_0^{QY_{\beta}}F(x){ d}x{
d}G(y)=\int_0^1\int_a^{Q[(1-\beta)y+\beta\mu]}\frac{x-a}{b-a}{
d}x{ d}G(y)
=\frac{Q^2(\mu^2+(\beta-1)^2\sigma^2)-2a\mu Q+a^2}{2(b-a)}$
(9)
由此说明$(-\Pi(Q,\beta))^+ $是关于$Q$和$\beta$的联合凸函数,从而得证$\Psi(Q,\beta)=-E(-\Pi(Q,\beta))^+$是关于$Q$和$\beta$的联合凹函数. 因此,零售商的期望效用$EU(Q,\beta)=E\Pi(Q,\beta)+\lambda\Psi(Q,\beta)$是关于$Q$和$\beta$的联合凹函数,从而问题(8)存在唯一最优解,且最优解由$EU(Q,\beta)$关于$Q$和$\beta$ 的联立一阶方程组给定. 证毕.
$\bigg(-\Pi\bigg(\frac{Q_1+Q_2}{2},\frac{\beta_1+\beta_2}{2}\bigg)\bigg)^+ \le\bigg(\frac{-\Pi(Q_1,\beta_1)-\Pi(Q_2,\beta_2)}{2}\bigg)^+\le\frac{(-\Pi(Q_1,\beta_1))^+}{2}+\frac{(-\Pi(Q_2,\beta_2))^+}{2}.$
其中,$R_1$和$R_2$分别表示$\Pi_1(Q,\beta)\le0$和$\Pi_2(Q,\beta)\le0 $的定义域. 结合式(6),通过图 1分析$R_1$和$R_2$所表示的区域.
$\Psi(Q,\beta)=\bigg[\int\int_{R_1}\Pi_1(Q,\beta){ d}F(x){}G(y)+\int\int_{R_2}\Pi_2(Q,\beta){ d}F(x){ d}G(y)\bigg]$
(10)
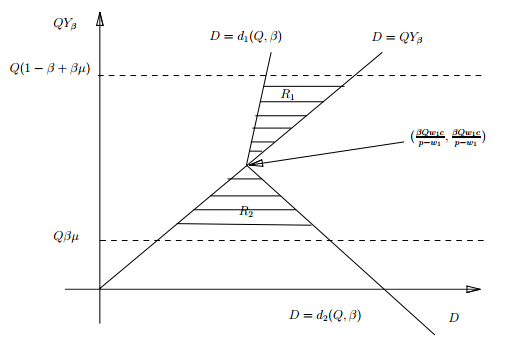
图 1 提前支付情况下零售商利润分析图
2.2 模型参数分析
$\left\{
\begin{array}{lll}
\frac{\partial EU(Q,\beta)}{\partial Q}&=&(w_0-w_1)\mu-\beta
w_1c-(w_0-s)\int_0^1y_{\beta} F(Qy_{\beta}){
d}G(y)\\
&&-\lambda\int_0^1[(w_1-s)y_{\beta}+\beta w_1c]
F(d_1(Q,\beta)){
d}G(y)=0\\
\frac{\partial EU(Q,\beta)}{\partial
\beta}&=&-Qw_1c-(w_0-s)\int_0^1F(Qy_{\beta})Q(\mu-y){
d}G(y)\\
&&-\lambda\int_0^1[(w_1-s)(\mu-y)+w_1c]QF(d_1(Q,\beta)){
d}G(y)=0
\end{array}
\right.$
(11)
$F(d_1(Q,\beta))]{ d}G(y)>0$,则最优提前支付比例增大,即$\beta_F^*\ge\beta_{F_1}^*$; 否则最优提前支付 比例减小.
$+w_1c]Q[F_1(d_1(Q,\beta))-F(d_1(Q,\beta))]{}G(y)$,上面式子可能大于零也可能小于零,从而可以得到性质2的第三部分. 证毕.
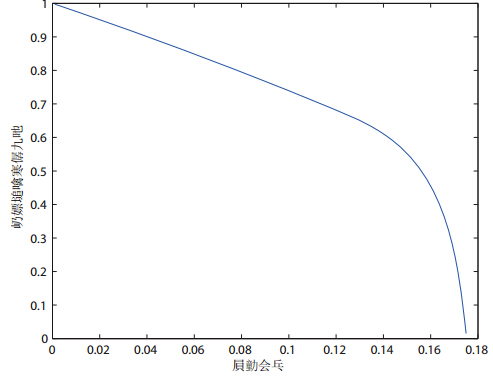
图 2 最优提前支付比例随资金成本变化图 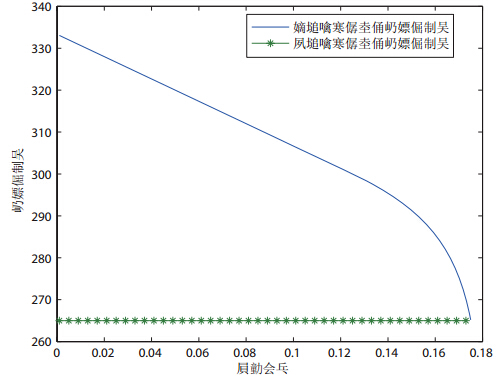
图 3 最优订货量随资金成本变化图 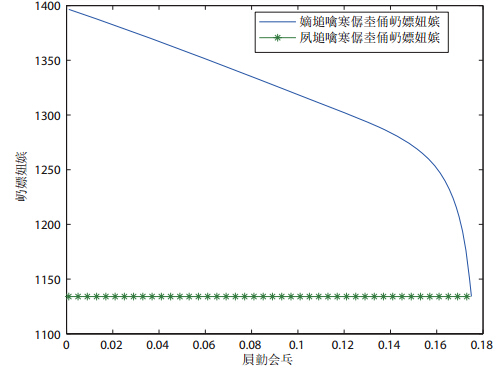
图 4 最优效用随资金成本变化图
| [1] | Kleindorfer P R, Saad G H. Managing disruption risks in supply chains[J]. Production and Operations Management, 2005, 14(1): 53-68. |
| [2] | Porteus E L. Foundations of stochastic inventory theory[M]. Stanford: Stanford University Press, 2002. |
| [3] | Wang C X, Webster S. The loss-averse newsvendor problem[J]. Omega, 2009, 37(1): 93-105. |
| [4] | Kahn J A. Why is production more volatile than sales? Theory and evidence on the stockout-avoidance motive for inventory holding[J]. Quarterly Journal of Economics, 1992, 107(2): 481-510. |
| [5] | Camerer C, Babcock L, Loewenstein G, et al. Labor supply of New York City cabdrivers: One day at a time[J]. The Quarterly Journal of Economics, 1997, 112(2): 407-441. |
| [6] | Schweitzer M E, Cachon G P. Decision bias in the newsvendor problem with a known demand distribution: Experimental evidence[J]. Management Science, 2000, 46(3): 404-420. |
| [7] | Wang C X. The loss-averse newsvendor game[J]. International Journal of Production Economics, 2010, 124(2): 448-452. |
| [8] | Ma L. Loss-averse newsvendor problem with general profit target[J]. International Journal of Information and Decision Sciences, 2008, 1(2): 145-163. |
| [9] | Ma L, Zhao Y, Xue W, et al. Loss-averse newsvendor model with two ordering opportunities and market information updating[J]. International Journal of Production Economics, 2012, 140(2): 912-921. |
| [10] | 沈厚才,徐进,庞湛.损失规避偏好下的定制件采购决策分析[J].管理科学学报, 2005, 7(6): 37-45.Shen Houcai, Xu Jin, Pang Zhan. Decision analysis for order-specific component procurement with loss-averse utility[J]. Journal of Management Sciences in China, 2005, 7(6): 37-45. |
| [11] | Wang C X, Webster S. Channel coordination for a supply chain with a risk-neutral manufacturer and a loss-averse retailer[J]. Decision Sciences, 2007, 38(3): 361-389. |
| [12] | Shen H, Pang Z, Cheng T C E. The component procurement problem for the loss-averse manufacturer with spot purchase[J]. International Journal of Production Economics, 2011, 132(1): 146-153. |
| [13] | Liu W, Song S, Wu C. Impact of loss aversion on the newsvendor game with product substitution[J]. International Journal of Production Economics, 2013, 141(1): 352-359. |
| [14] | Ma L J, Xue W L, Zhao Y X, et al. Loss-averse newsvendor under supply uncertainty, under review[J]. The Journal of Operational Research Society, 2014, 1: 29. |
| [15] | Liu S, So K C, Zhang F. Effect of supply reliability in a retail setting with joint marketing and inventory decisions[J]. Manufacturing & Service Operations Management, 2010, 12(1): 19-32. |
| [16] | Tang S Y, Kouvelis P. Supplier diversification strategies in the presence of yield uncertainty and buyer competition[J]. Manufacturing & Service Operations Management, 2011, 13(4): 439-451. |
| [17] | Hu X, Gurnani H, Wang L. Managing risk of supply disruptions: Incentives for capacity restoration[J]. Production and Operations Management, 2013, 22(1): 137-150. |
| [18] | Xu M, Lu Y. The effect of supply uncertainty in price-setting newsvendor models[J]. European Journal of Operational Research, 2013, 227(3): 423-433. |
| [19] | Cho S H, Tang C S. Advance selling in a supply chain under uncertain supply and demand[J]. Manufacturing & Service Operations Management, 2013, 15(2): 305-319. |
| [20] | 王晓立,马士华.供应和需求不确定条件下物流服务供应链能力协调研究[J].运筹与管理, 2011(2): 44-49.Wang Xiaoli, Ma Shihua. Research on capacity coordination in a logistics service supply chain with demand and supply uncertainties[J]. Operations Research and Management Science, 2011(2): 44-49. |
| [21] | Luo J. Buyer-vendor inventory coordination with credit period incentives[J]. International Journal of Production Economics, 2007, 108(1): 143-152. |
| [22] | Sarmah S P, Acharya D, Goyal S K. Coordination and profit sharing between a manufacturer and a buyer with target profit under credit option[J]. European Journal of Operational Research, 2007, 182(3): 1469-1478. |
| [23] | 于丽萍,黄小原,李丽君.非对称信息下供应链中商业信用激励契约研究[J].东北大学学报(自然科学版), 2008(1): 141-144.Yu Liping, Huang Xiaoyuan, Li Lijun. On the incentive contract to keep trade credit with asymmetric information in supply chain[J]. Journal of Northeastern University (Natural Science), 2008(1): 141-144. |
| [24] | Maiti A K, Maiti M K, Maiti M. Inventory model with stochastic lead-time and price dependent demand incorporating advance payment[J]. Applied Mathematical Modelling, 2009, 33(5): 2433-2443. |
| [25] | Thangam A. Optimal price discounting and lot-sizing policies for perishable items in a supply chain under advance payment scheme and two-echelon trade credits[J]. International Journal of Production Economics, 2012, 139(2): 459-472. |
| [26] | 曾文瑛,胡昊.供应风险条件下零售商订货及提前支付策略研究[J].科学技术与工程, 2012, 20(10): 2395-2399.Zeng Wenying, Hu Hao. Optimal order decision and advanced payment strategy of retailer under supply risk[J]. Science Technology and Engineering, 2012, 20(10): 2395-2399. |
| [27] | 代大钊,张钦红.资金约束条件下考虑信用风险的供应链商业信用决策研究[J].上海管理科学, 2013(3): 62-66.Dai Dazhao, Zhang Qinhong. Study on optimal trade credit policy under stock-dependent demand and credit risk[J]. Shanghai Management Science, 2013, 35(3): 62-66. |
| [28] | Kahneman D, Tversky A. Prospect theory: An analysis of decision under risk[J]. Econometrica: Journal of the Econometric Society, 1979: 263-291. |
| [29] | Gupta D, Cooper W L. Stochastic comparisons in production yield management[J]. Operations Research, 2005, 53(2): 377-384. |
| [30] | 范笑燕. 基于交易信用的供应链协调策略研究[D]. 上海:上海交通大学, 2008.Fan Xiaoyan. Research on supply chain coordination with trade credit[D]. Shanghai: Shanghai Jiaotong University, 2008. |



