Optimal pricing research with speculators and strategic consumers
0 引言
市场上销售的很多产品都有数量上的限制,或者一些产品的市场需求很大,而短期供应能力有限. 这类产品包括一些热销的电子产品,如iPhone4和iPad,NBA热门场次或者季后赛阶段的门票,一些明星的演唱会门票. 由于短期之内产品数量的限制,使得这类产品不能满足消费者大量的需求,从而导致了需求缺口. 通过正规渠道没有购买到产品的消费者将会转向"黄牛"或者在线拍卖市场(如eBay)购买,我们称之为再销售市场. 而且,消费者通常愿意为这些产品支付更高的产品价格. 两类市场上产品价格的不同,为投机商的出现提供了更好的机会. 与购买产品用来使用的终端消费者不同,投机商购买产品并不是为了消费,而是以再销售获取利润为目的.
虽然投机商的出现令零售商们很头疼. 但在线拍卖市场一直在稳定的增长,其中包括美国两家增长较快的公司Stub Hub和Tickets Now,预计它们到2012年演唱会和体育比赛的门票收入会达到45亿美元,这一数字将远远超出零售商们的22亿美元的销售额(Mulpuru等[1]). 这种收入差距大多数来源于愿意支付更高价格来购买产品的消费者,例如,在线拍卖商在NBA决赛期间的利润可以超过5000美元,由于需求巨大,这些门票的价格可以达到35000美元. 然而,投机商的每次行为并不是都能获得利润,eBay估计它们有45%的产品将会亏本甩卖. 面对投机商的这种行为,零售商需要根据库存产品的数量,来决定如何制定相应的价格策略成为目前一个值得研究的重要课题.
当顾客在策略性地选择购买时机时,影响动态定价策略的因素增多而使策略设计变得更为复杂. 最近几年,策略性顾客行为引起了运作管理研究者的关注,出现了许多考虑策略性顾客的理论研究文献[2]. 已有的关于策略性顾客行为的文献均是针对顾客策略行为进行相应的管理策略设计研究. 例如,Harris等[3]研究了当不知道消费者保留价格和产品供应能力有限的情况下,利用机制设计理论分析了厂商的最优动态定价. Talluri等[4]指出,将策略性顾客行为模型化根本上是一种机制设计(mechanism design). Ovchinnikov等[5]研究了当策略型消费者等待厂商降价时的最优动态定价策略. Aviv等[6]研究了面临策略性顾客时,销售有限数量的时装的最优定价问题,销售商作为Stackelberg领导者宣布价格策略,顾客作为跟随者决定购买行为,证明发现存在子博弈完美纳什均衡. Su[7]考虑了策略性顾客和非策略性顾客组成的异质人群,发现无论降价还是提价,最优价格路径均依赖于市场顾客构成. Elmalghraby[8]研究了面对多单位需求的策略性顾客的最优降价机制. Levin等[9, 10, 11]研究了面对策略性顾客时垄断易逝品销售商的动态定价. Zhang等[12]研究了销售期为两周期时消费者的策略性购买行为对厂商动态定价的影响. 刘晓峰等[13]研究了基于策略性顾客的最优动态定价问题. 杨慧等[14]}$研究了策略型消费者和短视型消费者的不同特征,其数值试验表明,产品降价幅度、两类消费者总的期望购买数量和企业总的期望利润会随着策略型消费者所占比例的增大而减小. Swinney[15]考虑零售商在面对策略性消费者时,当消费者对产品的保留价格不一致时,如何采用快速响应策略来平衡供需矛盾,作者论证当价格持续上升时或不满意的顾客能返回购物时,快速响应策略能给零售商带来额外的收益.
跟本研究相关的另一个分支是投机商行为,较早研究投机商的学者是Swofford[16],在文章中假设投机商比零售商的风险厌恶程度更低,投机商作为中间人获得有风险的额外收益. Courty[17]研究了后进入市场的消费者具有更高的保留价格的情况下,投机商将囤积的产品卖给这些具有更高保留价格的消费者,从而获得更高的利润. Karp等[18]投机商能很好地进行价格歧视,从而最大化消费者的剩余价值. Su[19]同时也研究了存在投机商的动态定价策略,结论表明在实行固定价格时也能达到类似动态定价的效果. 跟本文最接近的是Wei等[20]将消费者分为短视型、策略性和投机者,研究表明在升价市场即类似机票市场临近时价格越高,最优价格策略是事先可定的静态形式,而在降价市场,最优价格策略是动态定价策略除非初始阶段是非常乐观并可以预计在后来会有很高的需求,此文给出了在什么条件下存在投机者能给零售商带来好处,但该文假定消费者对于产品的价值是同质的,本文将重点研究当消费者的保留价值随时间变化且面临缺货时,投机商和策略型消费者行为的共同作用下零售商如何决定最优价格策略,以实现经济利益最大化.
1 问题描述
一个具有垄断地位的产品零售商在有限的销售期内向消费者提供单位的产品. 在销售期内,零售商不能增加产品的数量,随着销售期的结束,最后未卖出的产品将完全退出市场.
本文使用的主要符号和假设如下:
1) 本文将产品销售期划分为两个周期,为周期1和周期2,对应的产品价格分别为$p_1$和$p_2$.
2) 高端和低端消费者的保留价格分别为$V_{ H}$和$V_{ L}$,且满足$V_{ L}3) 消费者无差别购买时的保留价格为$V$.
4) 消费者保留价格会随着销售期的变化而改变,本文假设变动系数为$\alpha$,其中$\alpha\geq 1$.
5) 周期1进入市场并且购买产品的投机商的数量为$S$.
6) 将消费者分为两种类型,第一种称为固定消费者(fixed consumer),其数量为$W$; 第二种称为随机消费者(random consumer),其数量为$X$.
7) 固定消费者中,策略型消费者所占比例为$$ $(0\leq \leq1)$,那么短视型消费者所占比例为$(1-)$.
8) 策略型消费者在周期2购买到产品的概率为$\beta$,其中$0\leq\beta\leq 1$.
9) 产品的单位成本、周期2结束后未卖出的产品残值均为0.
本文模型描述如下:
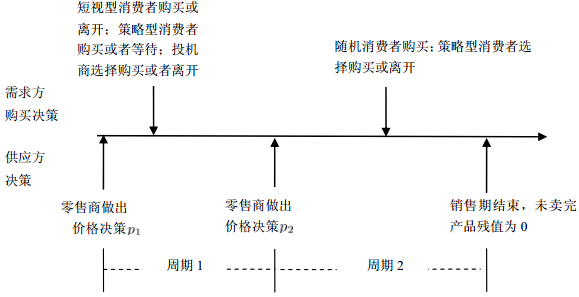
周期1,零售商首先制定一个产品价格决策$p_1$. 固定消费者$W$进入市场,其中短视型消费者根据自身保留价格的大小以及产品价格$p_1$决定购买或者离开市场; 策略型消费者根据自身保留价格、周期2的期望价格和周期2获得产品的概率,决定是立即购买还是延迟到周期2购买; 投机商根据周期2能够获得的期望利润决定是否购买产品.
周期2,零售商和投机商共同在市场中进行产品买卖行为. 而周期2新进入的消费者$X$和周期1选择推迟购买的策略型消费者一起共同组成产品购买者. 投机商根据零售商在周期2制定的价格$p_2$和$X$数量的大小决定产品的价格.
整个决策过程如图 1所示.
2 建立模型
2. 1 周期1
零售商在周期1的产品数量为$K$,设定的价格为$p_1$. 数量为$W$的固定消费者进入市场后,采取购买行动的短视型消费者的数量为$(1-)W\frac{V_{H}-p_1}{V_{ H}-V_{ L}}$,其余的短视型消费者将退出市场. 当且仅当$V-p_1\geq \beta(\alpha V-p_2)$时,策略型消费者不会等待而立即购买该产品,可以得到消费者的保留价格为:
|
$V=\frac{p_1-\beta p_2}{1-\alpha\beta}$
|
(1)
|
那么,周期1就采取购买行为的策略型消费者的数量为$W\frac{V_{ H}-V}{V_{ H}-V_{ L}}$. 另外,周期1购买产品的投机商的数量为$S$.
综上所述,周期1的产品销量为$(1-)W\frac{V_{ H}-p_1}{V_{H}-V_{ L}}+ W\frac{V_{ H}-V}{V_{ H}-V_{ L}}+S$,记为$K_1$. 因此,零售商周期1的收益为:
|
$\pi _{1R} = \left\{ {\frac{W}{V_{ H} - V_{ L} }(V_{ H} -
( {1 - } )p_1 - V) + S} \right\}p_1$
|
(2)
|
2. 2 现场销售期
周期2,零售商拥有的库存数量为$K-K_1$,投机商拥有的库存数量为$S$. 因此,此时供应方的产品库存数量为$S+K-K_1$. 消费者的数量包括选择等待在周期2购买的策略型消费者数量$W_2=W\frac{V-p_1}{V_{ H}-V_{L}}$和周期2新进入的随机消费者数量$X$,即消费者的数量总数为$X+W_2$.
根据周期2进入市场的随机消费者数量,本文将分三种情况讨论:随机消费者$X$很小,以至于$W_2+X<S$的情况; 随机消费者$X$中等,即$S\leq W_2+X① $W_2+X<S$时,即周期2实际市场需求量很小. 投机商会将产品价格设定为消费者最低保留价格$V_{ L}$,以便将库存中的产品全部卖出,此时零售商的销售量为0.
因此,零售商两周期的总收益为周期1的收益:
|
$\pi = \pi _{1R} = \left\{ {\frac{W}{V_{ H} - V_{ L} }(V_{
H} - \left( {1 - } \right)p_1 - V) + S} \right\}p_1$
|
(3)
|
令$\frac{\partial \pi }{\partial p_1 } = 0$,得到周期1的价格:
|
$p_1 = \frac{\left( {1 - \alpha \beta } \right)(\left( {V_{ H} -
V_{ L} } \right)S + WV_{ H} ) + \beta Wp_2 }{2W\left(
{\alpha \beta - \alpha \beta + 1} \right)}$
|
(4)
|
由于零售商在周期2不能卖出任何产品. 因此,他们可以将产品的价格设定为任何值,不失一般性,这里将产品的价格设定为$p_2=V_{ L}$.
此时,零售商的收益为:
|
$\pi ^\ast = \frac{(\left( {1 - \alpha \beta } \right)(V_{ H} W
+ \left( {V_{ H} - V_{ L} } \right)S) + \beta WV_{
L} )^2}{4W\left( {V_{ H} - V_{ L} } \right)\left( {1 -
\alpha \beta } \right)\left( {\alpha \beta - \alpha \beta +
1} \right)}$
|
(5)
|
故可以得到以下结论:
定理1 给定消费者保留价格区间、投机商和固定消费者的数量,则可以得到零售商的最优价格策略$p_1^{*}(\alpha,\beta)$和$p_2^*$,以及零售商的最大收益$\pi^*(\alpha,\beta)$.
② 当$S\leq W_2+X因此,零售商周期2的利润为:
|
$\pi _{2R} = p_2 \left( {X + W_2 - S} \right)$
|
(6)
|
其中,$W_2 = W\frac{V - p_1 }{V_{ H} - V_{ L} }$. 可以得到$\pi _{2R} = p_2 ( {X + W\frac{V - p_1 }{V_{ H}- V_{ L} } - S} )$.
将公式(1)代入公式(6),并令$\frac{\partial \pi_{2R}}{\partial p_2}=0$,可以得到零售商周期2制定的价格:
|
$p_2 = \frac{\alpha p_1 }{2} + \frac{\left( {1 - \alpha \beta }
\right)\left( {X - S} \right)\left( {V_{ H} - V_{ L} }
\right)}{2\beta W}$
|
(7)
|
零售商两周期的总收益为:
|
$\pi = \pi _{1R} + \pi _{2R} = p_2 \left( {X + W_2 - S} \right) +
\left\{ {\frac{W}{V_{ H} - V_{ L} }(V_{ H} - \left( {1 -
} \right)p_1 - V) + S} \right\}p_1$
|
(8)
|
将所得价格$p_2 $和公式(1)代入(8)式中,并令$\frac{\partial\pi}{\partial p_1}=0$,可以得到周期1的最优价格:
|
$p_1 = \frac{\left( {1 - \alpha \beta } \right)\left( {V_{ H} -
V_{ L} } \right)((S\left( {1 - \alpha } \right) + X\left( {1 +
\alpha } \right)) + 2V_{ H} W)}{W\left( {4 - 4\alpha \beta +
2\alpha \beta - \alpha ^2\beta } \right)}$
|
(9)
|
由此,可以得到如下命题.
命题 在上述两周期的零售商动态定价中,
如果已知策略型消费者所占比例$$ $(0\leq\leq 1)$,消费者周期2获得产品的风险系数$\beta$ $(0\leq\beta\leq 1)$,则可以得到零售商的最优价格策略:
|
$p_1^\ast = \frac{\left( {1 - \alpha \beta } \right)\left\{ {\left(
{V_{ H} - V_{ L} } \right)\left[{S\left( {1 - \alpha }
\right) + X\left( {1 + \alpha } \right)} \right] + 2V_{ H} W}
\right\}}{W\left( {4 - 4\alpha \beta + 2\alpha \beta -
\alpha ^2\beta } \right)}$
|
(10)
|
|
$p_2^\ast = \frac{\alpha p_1^\ast }{2} + \frac{\left( {1 - \alpha
\beta } \right)\left( {X - S} \right)\left( {V_{ H} - V_{ L}
} \right)}{2\beta W}$
|
(11)
|
|
$V^\ast = \frac{p_1^\ast - \beta p_2^\ast }{1 - \alpha \beta }$
|
(12)
|
|
$\pi ^\ast = \left( {X + W_2 - S} \right)p_2 ^\ast + \left\{
{\frac{W}{V_{ H} - V_{ L} }\left[{V_{ H} - \left( {1 -
} \right)p_1 ^\ast - V^\ast } \right] + S}
\right\}p_1 ^\ast$
|
(13)
|
③当$W_2+X\geq K_2+S$时,即周期2实际市场需求量很大. 此时,投机商会将产品的价格设定为最高保留价格$V_{ H}$,以便获取最大的利润. 由于消费者的数量足够大,零售商不用担心周期2产品卖不出去,就不会对产品打折,即周期2价格决策为$p_2=p_1$. 此时,消费者会首先从零售商那里购买产品,未在零售商那里购买到产品的消费者会转向投机商购买,但零售商和投机商的库存都会销售完. 此时,零售商卖出产品的数量为$K-K_1$,零售商周期2的收益为:
|
$\pi _{2R} = \left( {K - K_1 } \right)p_2 = \left( {K - K_1 }
\right)p_1$
|
(14)
|
此时,零售商两周期的总收益为:
|
$\pi = \pi _{1R} + \pi _{2R} = Kp_1$
|
(15)
|
3 数值分析
以下对市场上策略型消费者的比例,保留价格的变动系数,投机商的数量和周期2消费者购买到产品的概率对零售商的价格决策和收益的影响进行进一步的仿真分析. 不失一般性,令$V_{L}=1,V_{ H}=10,W=100,K=100,\alpha=1. 3$.
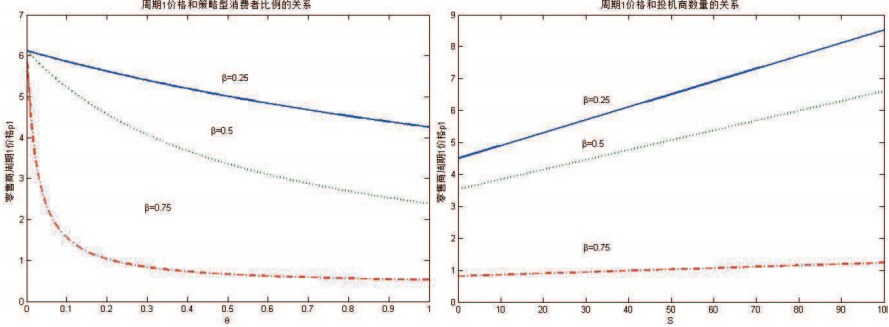
情形1 周期2随机消费者数量对零售商的两周期产品价格和利润没有影响. 令$S=25,=0. 25$分别得出了产品价格、零售商收益和策略型消费者与投机商数量的关系.
从图 2中可以看出,当周期2获得产品概率$\beta$不变时,周期1产品价格随着策略型消费者比例增加而减少; 同时,也可以看到随着产品获得概率的增加,产品价格反而降低. 这表明当策略型消费者比例增加或者周期2获得产品概率增加时,零售商更愿意制定较低的价格来促使消费者提前购买. 另外,产品价格也随着投机商数量的增加而增加.
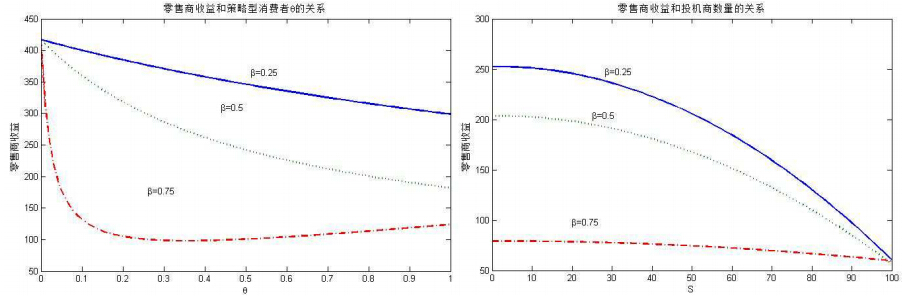
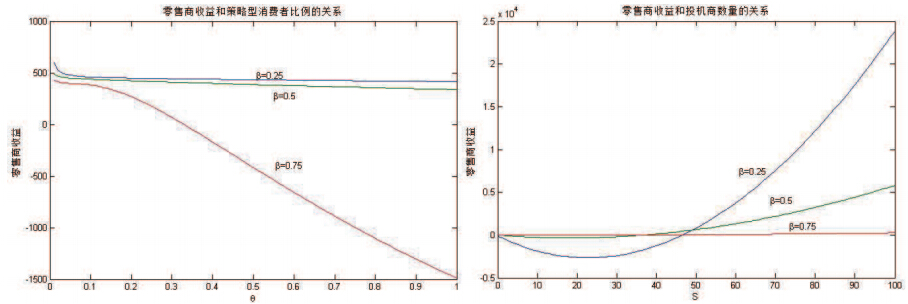
图 3中可以看出,当$\beta=0. 25$和$\beta=0. 5$时,零售商收益随着策略型消费者比例增加一直减少,但当$\beta=0. 75$时,随着策略型消费者比例增加,零售商收益呈现先减少后增加的现象; 投机商数量的增加会减少零售商的收益,并且收益减少的幅度随着投机商数量的增加越来越大. 同时,可以看到周期2产品获得概率的增加都会在不同程度上减少零售商的收益.
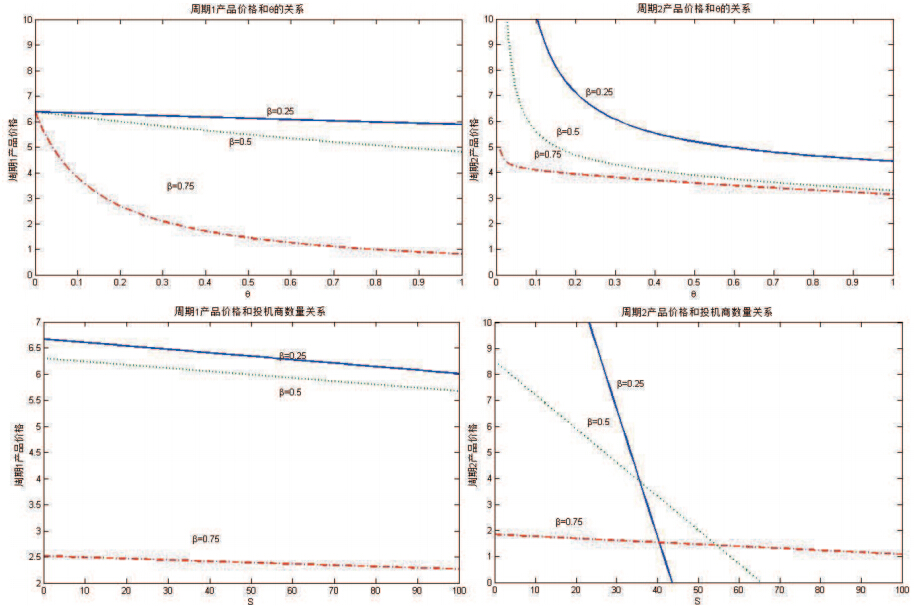
情形2 随机消费者数量对零售商产品价格和利润产生影响,并且满足周期2市场需求量中等的情况. 同样的,令$S=25,=0. 25,X=35$可以分别得出产品价格和零售商收益与策略型消费者和投机商数量的关系.
从图 4可以看出,零售商两周期的产品价格都随着策略型消费者比例的增加,这与情形1得出的结论相同; 但当投机商数量逐渐增加时,零售商的价格会逐渐减少,这与情况1的结论不同. 并且,当$\beta=0. 25,S\leq 30$和$\beta=0. 5,S\leq 18$时,零售商周期2的产品价格要高于周期1的产品价格,这表明当投机商数量很少和产品获得概率较低时,零售商更愿意在周期1制定较低的价格来吸引消费者的提前购买.
从图 5可以看出,零售商的收益随着策略型消费者的比例的增加而减少,与情形1的结论相似,但当$\beta=0. 25$和$\beta=0. 5$时,策略型消费者对收益的影响并不大,零售商收益降低的幅度也很小,但当$\beta=0. 75$时,零售商收益随着策略型消费者比例的增加产生显著减少; 另外,从总体趋势上看,投机商数量的增加能够增加零售商的收益,这与情形1的结论不同,并且当$\beta=0. 25$和$\beta=0. 5$,随着投机商数量的增加零售商的收益会呈现先减少,再增加的趋势,当$\beta=0. 75$时,零售商的收益基本没有什么变化.
情形3 随机消费者数量很庞大的情况,零售商此时一定会将产品的价格制定为消费者的最高保留价格,且此时对收益的影响因素为零售商拥有的产品库存,鉴于零售商产品库存在短期之内不能改变,因此本文不做进一步讨论.
4 结论
大多数的策略型消费者的研究中,通常没有考虑到消费者保留价格的变动、市场中有新的消费者加入和市场中热销商品会有投机商出现的情况. 消费者会依据市场状态和零售商产品的库存和价格策略来决定自己的购买时机,投机商同样也会根据市场需求状况和现阶段的产品价格以及产品价格预期来确定是否进入市场进行投机行为,他们的行为特征会对零售商的价格决策和总体收益产生重大影响. 本文考虑一个拥有固定库存产品的垄断零售商,在面对策略型消费者的延迟购买和投机商的投机行为时的价格决策. 同时,本文基于Stackelberg博弈模型,刻画了市场需求方和供应方的博弈,通过将消费者进行进一步的细分,得出了零售商使自身收益最大化的价格决策策略,从而避免了零售商收益的损失.
本文虽然建立了零售商的价格决策模型,但只考虑了消费者的保留价格服从均匀分布的情况,同时也只将消费者划分为两种类型. 对本文的扩展包括以下几个方面. 首先,消费者的保留价格属于泊松分布的情况,考虑更复杂情况下零售商的价格决策. 其次,考虑消费者、零售商和投机商的风险偏好. 最后,通过制定"收益共享"来考虑零售商和投机商合作的情况.