文章信息
- 王志学 , 刘建伟 , 艾倩颖 . 2016
- WANG Zhixue, LIU Jianwei, AI Qianying . 2016
- 细粒度访问控制的电子健康网络双向认证方案
- Authentication for Fine-Grained Access Control in Electronic Health Network
- 武汉大学学报(理学版), 2016, 62(3): 255-260
- Journal of Wuhan University(Natural Science Edition), 2016, 62(3): 255-260
- http://dx.doi.org/10.14188/j.1671-8836.2016.03.008
-
文章历史
- 收稿日期:2015-05-09

近年来,随着信息技术的高速发展,一种新型网络——电子健康网络出现了,人们享受到了更加实时、便捷、高效的医疗服务[1].然而电子健康网络给人们带来便利的同时,也带来了巨大的安全隐患[2],其中,用户信息的非授权访问便是一项重大风险[3].一方面,病人的健康信息具有高度的隐私性,如被非法获取将有可能对病人造成严重的生理威胁;另一方面,医疗与健康信息如果遭到非法篡改,可能使医生误诊、开出错误的处方或采取错误的治疗措施,这将给患者带来健康乃至生命威胁.安全的接入认证方案正是解决上述问题的一种有效措施.
Sun等提出了一个病患隐私医疗系统,利用现有的密码学技术为病患提供隐私保护[4].Chen等[5]研究了在线医疗数据在私人控制下的紧急访问授权;Guo等[6]提出了一种电子健康网络的属性基认证系统;Akinyele等[2]设计并实现了一种基于属性基加密的自保护电子病历,可实现电子病历存取的细粒度访问控制.
电子健康网络是一种多属性的网络,其中的实际参与者(个人或者机构)具有各种各样的属性(如病人、医生、医院等),而不同属性的参与者拥有不同的访问权限(如某些病人的病历只能被其主治医生查看,而护士无法访问).目前应用最广泛的用户名密码身份认证方式不仅已被认为是弱安全的[7],而且无法满足上述网络需求.在这样的网络特性下,新兴的基于属性的签名给了我们设计接入认证方案的新思路.
Yang等[8]提出了一种基于模糊身份的签名方案,当验证者与签名者的属性集合匹配满足门限值时,验证者可以验证签名的有效性,该方案策略比较简单,只支持属性的与门操作;Maji等[9]提出了一种ABS方案,可以实现由与门和或门组成的访问控制结构;Guo等[10]提出了一种基于访问树的ABS方案,同样可以实现与门和或门,但与文献[9]中方案一样需要在初始化阶段确定属性,且公共参数长度与属性个数线性相关,这在多属性的电子健康网络中将不利于系统的扩展,并给系统增加了较重的负担.
为解决电子健康网络中的接入认证问题,本文提出了一种细粒度访问控制的双向接入认证方案,并且针对电子健康网络中的实际需求,提出了一种新型ABS方案.
1 预备知识 1.1 双线性映射设G0和G1分别为两个有限循环群,并有相同的素数阶p,设g是G0的生成元,如果映射e:G0×G0→G1满足如下性质:
1) 双线性特性:对于所有的g,h∈G0,a,b∈Zp,有e(ga,hb)=e(g,h)ab成立;
2) 非退化性:G0群中至少存在一个元素g,使得计算后的e(g,g)在G1群中有阶数p;
3) 可计算性:存在有效的算法,使得所有的u,v∈G0,可以有效计算出e(u,v)的值.
1.2 访问结构
设U为属性域,访问结构指一个非空的属性集合A,
一个属性域U上的秘密共享方案Π在Zp上是线性的[11] ,如果:
1) 每一个属性对于秘密s∈Zp的共享构成一个Zp上的向量;
2) 对于U上任意的访问结构A,存在一个共享生成矩阵M∈Zpl×n,以及一个矩阵的行到属性的映射ρ:[l]→U.选取向量v=(s,r2,r3,…,rn),其中s是要共享的秘密,r2,r3,…,rn∈Zp为随机选取,则Mv即为由Π得到的s的共享向量,(Mv)i属于属性ρ(i).
按照如上方法定义的LSSS方案具有线性可重构性:假设访问结构A由(M,ρ)所描述,对于授权集合S∈A,设I={i:i∈l∧ρ(i)∈S},对于有效的秘密共享{λi=(Mv)i}i∈I,存在常数集ωi∈Zp}i∈I,使得$\sum\limits_{i\in I}^{{}}{{}}$ωiλi=s.对于非授权集合S′则不存在这样的常数集ωi},在此情况下,设I′={i:i∈l∧ρ(i)∈S′},存在向量ω∈Zp1×n,其中第一个元素ω1为非零元素,并且ωMi=0,i∈I′.
1.4 基于属性的签名在基于属性的签名方案中,签名者的私钥与其属性相关,在签名时,签名者用私钥和其声称满足的访问结构对消息进行签名,验证者则利用公共参数对签名进行验证.一个基于属性的签名由初始化算法(Setup)、私钥生成算法(KeyGen)、签名算法(Sign)和验证算法(Verify)四个算法组成,具体描述如下:
1) (pp,msk)← Setup(λ):根据输入的安全参数λ,输出公共参数pp及系统主密钥msk.
2) sk← KeyGen(msk,S):根据输入的系统主密钥msk和用户属性集S,输出用户私钥sk.
3) σ← Sign(sk,γ,S,m):根据输入的用户私钥sk,签名者所声称满足的访问结构γ,签名属性集S以及消息m,输出签名σ.
true or false ← Verify(σ,pp):根据输入的签名σ及公共参数pp,输出验证结果true 或者false.
2 本文方案本节首先提出一种适用于电子健康网络的接入认证方案,该方案可以利用现有的ABS方案,满足双向认证及访问控制的需求.然而现有的ABS方案均须在初始化阶段确定属性数量,而且公共参数的长度随属性数量的增加而线性增加.对于电子健康网络而言,上述特点将极不利于系统的扩展,并给系统带来了沉重的负担.为解决这一问题,本节接着提出一种新型ABS方案,该方案可实现细粒度访问控制,灵活支持与门、或门和门限操作,无需在初始化阶段对属性数量进行限制,可方便地对系统进行扩展,并且公共参数长度为常数,可有效减轻系统的负担.
2.1 接入认证方案如图1所示,私钥生成中心(private key generator,PKG)首先对参与者(包括用户(User)和认证服务器(authentication sever,AS))的身份进行验证,计算生成与其属性相对应的私钥,并以安全方式发送给参与者.接下来User向AS发起认证请求,AS收到请求后,将与User进行交互,完成双向的身份认证.具体认证过程如下所述:
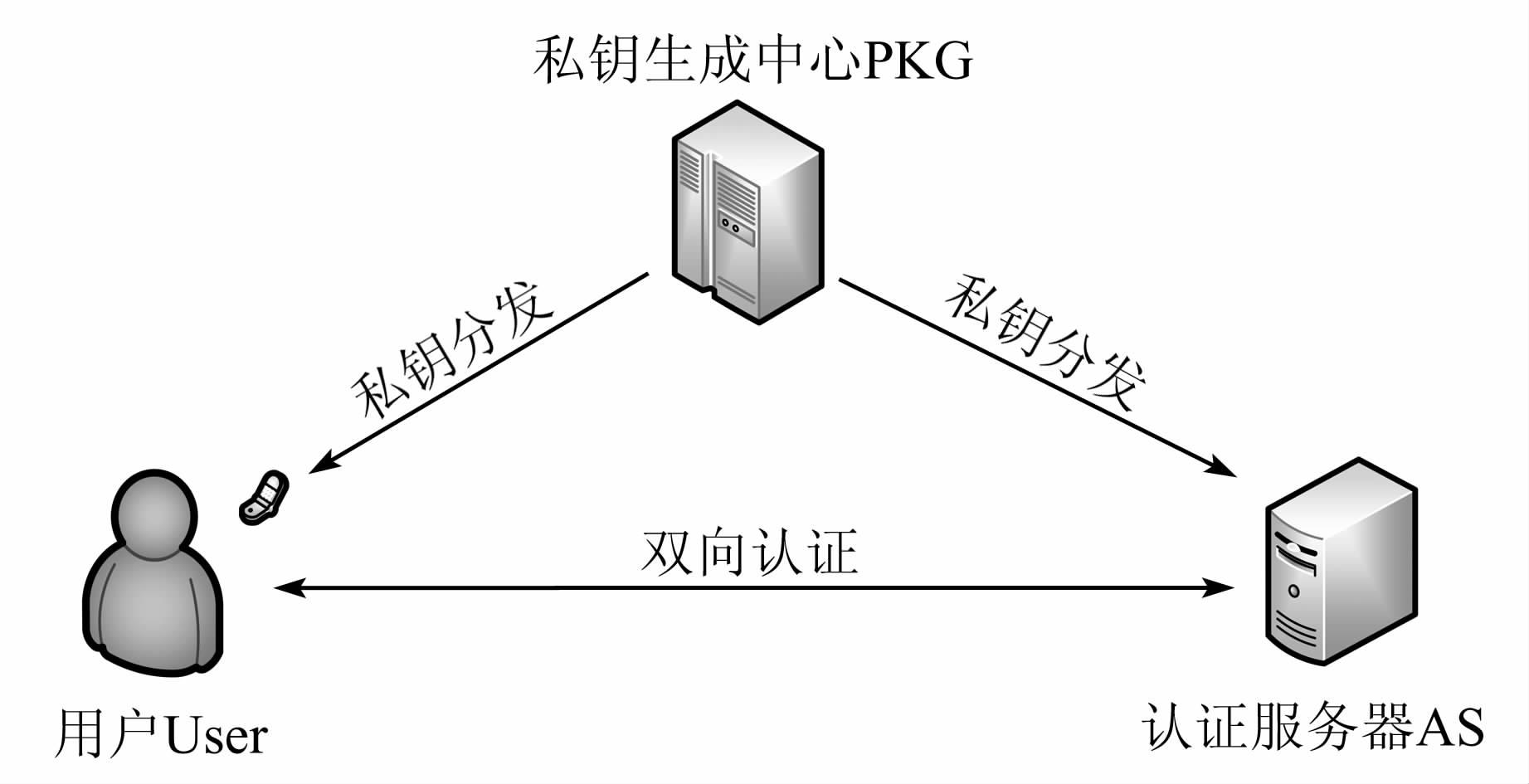
|
| 图 1 系统模型 Figure 1 System model |
1) PKG执行Setup算法,得到公共参数pp及系统主密钥msk,其中pp对外公开,msk由PKG保留.
2) 认证参与者(User和AS)分别向PKG请求私钥,PKG执行KeyGen算法,根据参与者所拥有的属性生成相应的密钥,并将密钥以安全方式发送给参与者.
2.1.2 接入认证1) User向AS发起认证请求,生成AS所应满足的访问结构γA,并将γA发送给AS.
2) AS收到请求后,首先生成时戳TA,并生成User所应满足的访问结构γU,然后根据User所要求的访问结构γA及自己的私钥skA对TA及γU进行签名得到σA,并将σA发送给User.
3) User收到σA后首先验证签名是否有效,验证成功后检查时戳TA是否新鲜,然后生成当前时戳TU,根据访问结构γU及自己的私钥skU对TU进行签名得到σU,并将σU发送给AS.
4) AS收到σU后,验证签名是否有效,验证成功后检查时戳TU是否新鲜,如果新鲜,则认证成功,完成认证.
协议流程如图2所示.
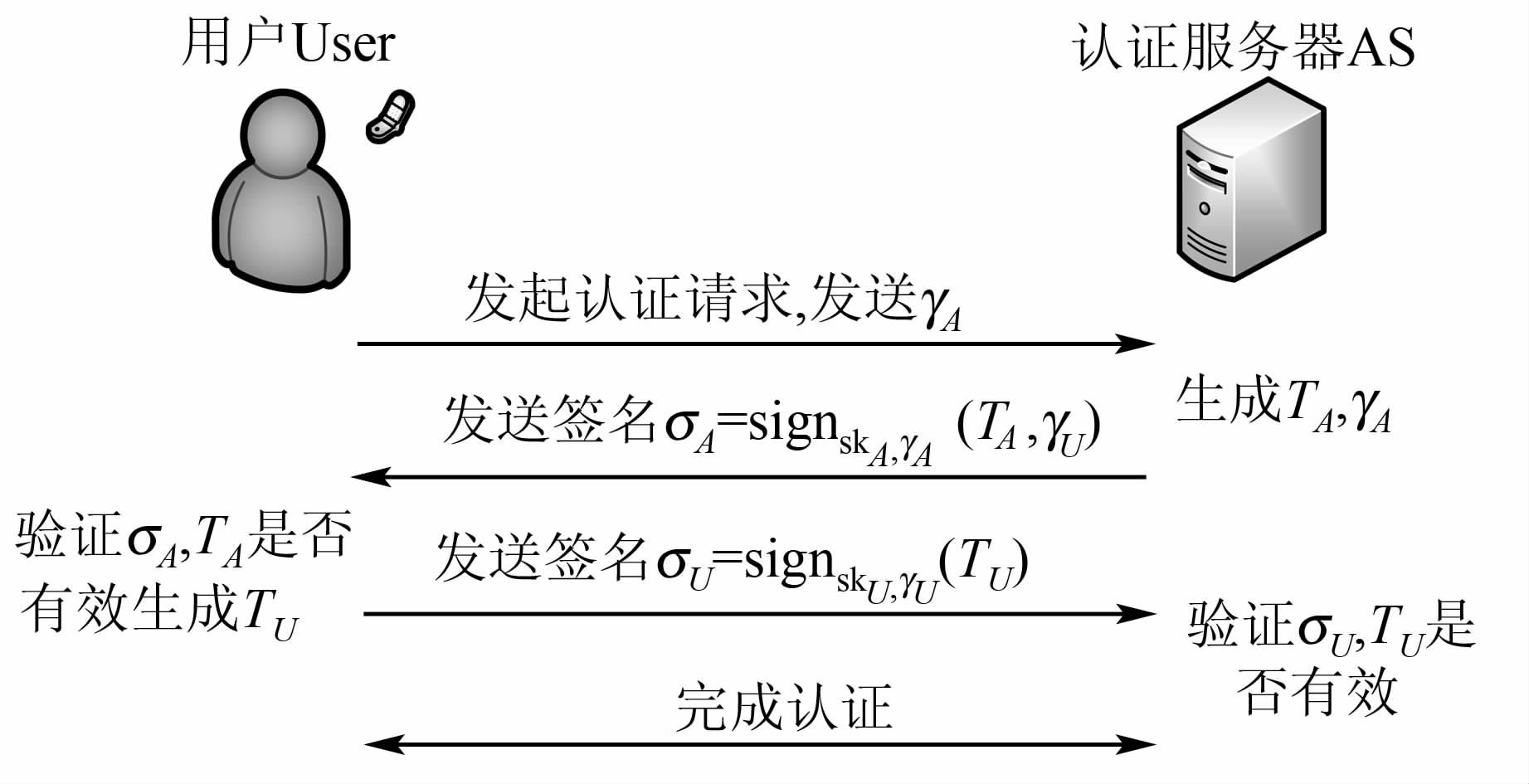
|
| 图 2 接入认证协议流程 Figure 2 Procedure of the access authentication protocol |
1) 重放攻击
方案引入时间戳机制,可保证信息的新鲜性,有效抵抗重放攻击.
2) 接入假冒攻击
方案中认证参与者的私钥经由PKG认证发放,没有相应属性的实体将无法得到相应的私钥,也就无法生成有效的签名.因此,可防止攻击者进行假冒攻击.
3) 共谋攻击
方案利用ABS进行构造,而抗共谋攻击为安全的ABS方案所固有的特性,不同的用户无法以共谋的方式生成合法的签名.因此本方案可抵抗共谋攻击.
4) 修改攻击
在本方案中,尽管认证消息可以被任何人所获取,但对于攻击者而言,如果对认证消息进行修改,在不知道密钥的情况下不可能生成合法的签名,也就使得攻击者不可能成功地修改User和AS之间传输的认证消息并通过认证.因此,本方案可抵抗修改攻击.
2.2 新型基于属性的签名方案本节提出了一种新型的基于属性的签名方案,该方案的设计思想来源于Rouselakis-Waters基于属性的加密方案[12].与加密方案不同,在签名方案中签名方需要将私钥嵌入到签名中,以使验证方可以验证签名方是否有与其属性对应的私钥,这就要求用户私钥在签名过程中得到有效保护,本方案在实现签名的过程中引入了随机参数z对用户私钥进行了随机化处理[13],可在正确验证签名的同时有效保护私钥信息.
2.2.1 方案构造方案包括4个基本算法:初始化算法(Setup)、私钥生成算法(KeyGen)、签名算法(Sign)和验证算法(Verify),具体实施过程如下:
1) (pp,msk)← Setup(λ):根据输入的安全参数λ,得到两个阶数为素数p的群G0、G1和一个双线性映射运算e:G0×G0→G1,设D=(p,G0,G1,e),属性域U=Zp.接下来随机选取g,u,h,w,v∈G0以及α∈Zp.可以得到公共参数pp=(D,g,u,h,w,v,e(g,g)α),系统主密钥msk=(α).
2)sk← KeyGen(msk,S):根据输入的系统主密钥msk和用户属性集S,输出相应的用户私钥.设用户的属性集S={A1,A2,…,Ak}⊆Zp,该算法随机选取k+1个指数r,r1,r2,r3,…,rk∈Zp,计算:
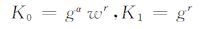
|
并对∀τ∈k,计算:
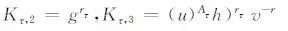
|
得到私钥sk=(S,K0,K1,{Kτ,2,Kτ,3}τ∈[k]).
3) σ← Sign(sk,γ,S,m):根据输入的签名者的用户私钥sk,签名者所声称满足的访问结构(M,ρ),签名属性集S以及消息m∈G1,输出签名σ.设I={i:ρ(i)∈S},随机选取z∈Zp,y=(s,y2,…,yn)∈Zn×1p,其中s为要共享的随机秘密.计算{λi=(My)i}i∈I,并随机选取{ti∈Zp}i∈I,接着计算:
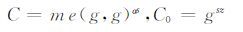
|
对于∀i∈I,计算:
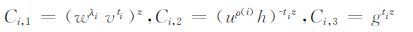
|
接下来计算:
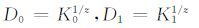
|
设J={j:j为属性ρ(i)在集合S中的索引与i相关},对于∀j∈J,计算:
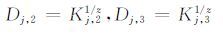
|
最终得到签名σ=(m,S,(M,ρ),C,C0,Ci,1,Ci,2,Ci,3i∈I,D0,D1,Dj,2,Dj,3j∈J).
4) true or false ← Verify(σ,pp):根据输入的签名σ及公共参数pp,输出验证结果true 或者false.该算法首先计算常数集ωi∈Zp}i∈I使得$\sum\limits_{i\in I}^{{}}{{}}$ωiMi=(1,0,…,0),其中Mi为矩阵M的第i行,如果属性集S是授权集合,则必然存在这样常数集.接着判断对于∀i∈I,等式e(g-1,Ci,2)=e(Ci,3,uρ(i)h)是否均成立.如果不成立,则返回false;如果成立,则进行如下运算:
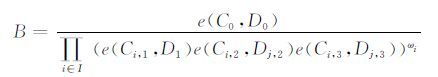
|
接着判断等式m=C/B是否成立,如果不成立,则返回false;如果成立,则返回true.
2.2.2 方案分析1) 正确性
若签名为合法生成,对于∀i∈I,有:e(g-1,Ci,2)=e(g,uρ(i)h)tiz以及e(Ci,3,uρ(i)h)=e(g,uρ(i)h)tiz,因此等式e(g-1,Ci,2)=e(Ci,3,uρ(i)h)成立.
由于签名私钥所对应属性满足访问控制结构,所以有∑i∈Iωiλi=s,因此:
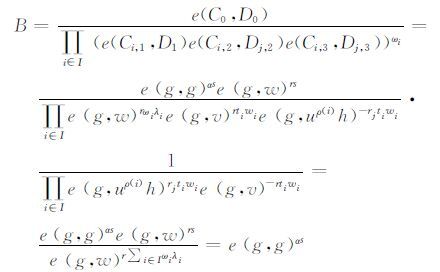
|
所以有m=C/B.
2) 不可伪造性
可以证明如果有算法能在多项式时间内伪造一个有效的签名,则文献[10]中的q-1困难问题假设以不可忽略的概率解决.
3) 功能分析
可以看到,本方案无须在初始化阶段确定属性数量,方便系统的扩展,而且通过一个哈希函数H:0,1*→G0,使得属性可以以任意字符串进行描述,并大大地提高了系统的灵活性.此外本方案的公共参数pp长度为常数,有效地降低了系统的负担.
3 效率分析 3.1 理论分析设k为生成私钥时所涉及的用户属性数量,l为用户进行签名是所用的属性数量.文中主要算法所需的各运算次数如表1所示.
| 基本算法 | EXP | M | P |
| Setup | 1 | - | 1 |
| KeyGen | 3k+4 | 2k+1 | - |
| Sign | 7l+4 | 2l+1 | - |
| Verify | 3l | 4l-1 | 5l+1 |
| 注:表中EXP和M分别为G0或G1群中的指数运算和乘法运算,P为线性对运算. | |||
我们针对本文方案的主要算法进行了仿真实现,所用语言为Java,通过调用jPBC函数库完成编程.运行环境为Windows 7 32位操作系统,Eclipse集成开发环境,PC配置为:3.4 GHz Intel Core i3-2130 CPU,2 GB RAM.在此环境下单次双线性对运算时间约为35 ms,指数运算约为33 ms.
如图3所示,在访问结构为“Director or Doctor or (Nurse and level > 2)”的情况下,属性为“Doctor”的用户进行签名认证.经验证签名有效.
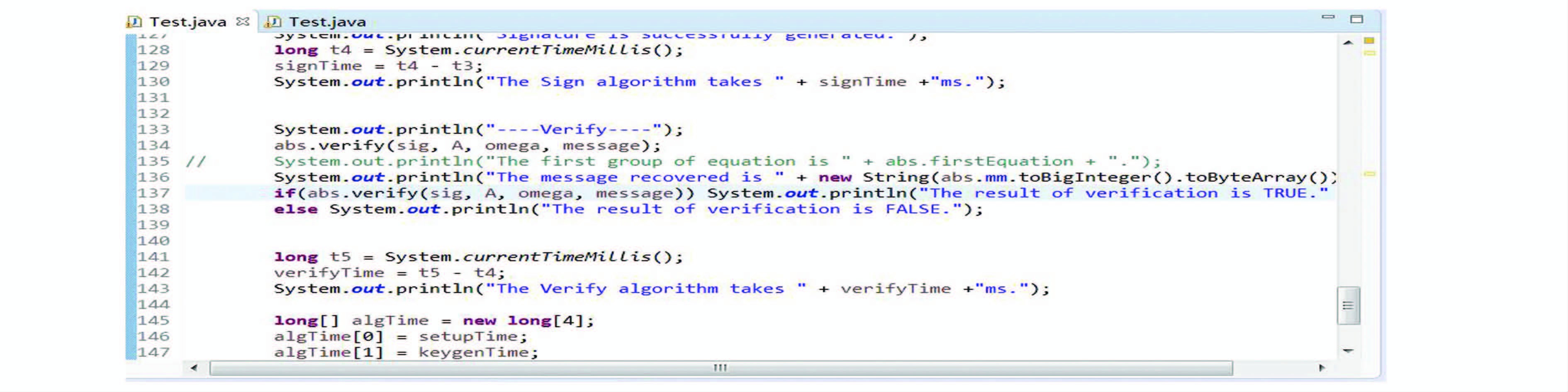
|
| 图 3 签名验证成功示例 Figure 3 A success sample for verification |
如图4所示,在访问结构为“Director or Doctor or (Nurse and level > 2)”的情况下,属性为“Patient”的用户进行签名认证.经验证签名无效.
|
| 图 4 签名验证失败示例 Figure 4 A failure sample for verification |
图5分别代表Setup、KeyGen、Sign和Verify算法的运行时间,其中横轴代表属性个数,纵轴代表运行时间.
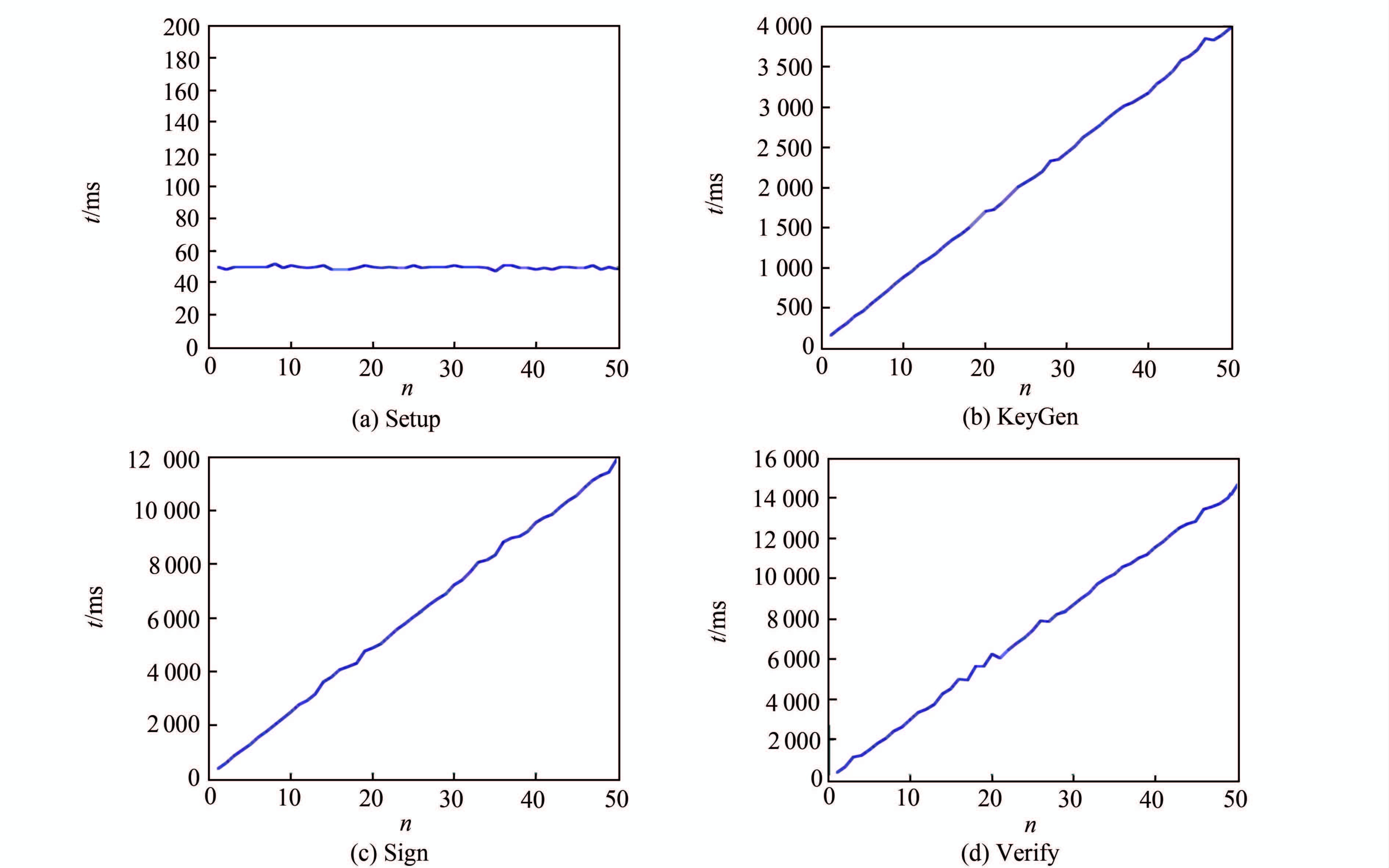
|
| 图 5 4个算法运行时间 Figure 5 The performance time for four algorithms |
可以看到,Setup算法的运行时间随属性的增加没有发生变化,KeyGen、Sign和Verify算法的运行时间随着属性的增加而线性增加,这与算法的执行过程是相符的.在电子健康网络的实际应用中,尽管整个属性域的属性数量很大,但对于具体的单次认证,所用到的属性个数并不会太多,因而本方案在实际应用中具有较高的效率.
4 结论本文提出的新型ABS方案,将本签名运用到接入认证方案中,可实现细粒度访问控制,在实际应用中具有良好的适应性和灵活性;并且无须在初始化阶段对属性数量进行限制,从而可方便地对系统进行扩展;此外,由于公共参数长度为常数级,系统负担得到有效减轻.通过安全分析可知,本方案可抵抗重放攻击、假冒攻击、共谋攻击和修改攻击等行为,有效防止非授权访问.仿真结果显示本方案具有良好的实用性和有效性.
| [1] | DOMINGO M C. Managing healthcare through social networks[J]. Computer, 2010, 43 (7) : 20 –25. |
| [2] | AKINYELE J A, LEHMANN C U, GREEN M D, et al. Self-protecting electronic medical records using attribute-based encryption[DB/OL]. [2015-01-23].http://www.researchgate.net/publication/220335968_Self-Protecting_Electronic_Medical_Records_Using_Attribute-Based_Encryption. |
| [3] | NARAYAN S, Gagné M, SAFAVI-NAINI R. Privacy preserving EHR system using attribute-based infrastructure[DB/OL]. [2015-02-01].http://dl.acm.org/ft_gateway.cfm?id=1866845. |
| [4] | SUN J Y, ZHU X Y, ZHANG C, et al. HCPP: Cryptography based secure EHR system for patient privacy and emergency healthcare[DB/OL]. [2015-03-01].http://www.fang.ece.ufl.edu/mypaper/icdcs11sun.pdf. |
| [5] | CHEN T T, ZHONG S. Emergency access authorization for personally controlled online health care data[J]. Journal of Medical Systems, 2012, 36 (1) : 291 –300. |
| [6] | GUO L K, ZHANG C, SUN J Y, et al. PAAS: A privacy-preserving attribute-based authentication system for eHealth networks[DB/OL]. [2015-02-03].http://www.computer.org/csdl/proceedings/icdcs/./4685a224.pdf. |
| [7] | 张虎强, 洪佩琳, 李津生, 等. 用户名密码认证方案的安全性分析及解决方案[J]. 计算机工程与应用, 2006 ,42 (33) : 102 –106. ZHANG H Q, HONG P L, LI J S, et al. Security analysis and solution of user password identification scheme[J]. Computer Engineering and Applications, 2006, 42 (33) : 102 –106. |
| [8] | YANG P, CAO Z, DONG X. Fuzzy identity based signature[DB/OL]. [2015-03-09].http://www.researchgate.net/publication/220336216_Fuzzy_Identity_Based_Signature . |
| [9] | MAJI H, PRABHAKARAN M, ROSULEK M. Attribute-based signatures: Achieving attribute-privacy and collusion-resistance[DB/OL]. [2015-01-23].http://eprint.iacr.org/2008/328.pdf. |
| [10] | GUO S Q, ZENG Y P. Attribute-based signature scheme[DB/OL]. [2015-03-10].http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=4511620. |
| [11] | BEIMEL A. Secure Schemes for Secret Sharing and Key Distribution[DB/OL]. [2015-01-23].http://www.cs.bgu.ac.il/~beimel/Papers/thesis.pdf. |
| [12] | ROUSELAKIS Y, WATERS B. Practical constructions and new proof methods for large universe attribute-based encryption[C]//Proceedings of the 2S013 ACM SIGSAC Conference on Computer & Communications Security. New York:ACM, 2013: 463-474. |
| [13] | GREEN M, HOHENBERGER S, WATERS B. Outsourcing the decryption of ABE ciphertexts[DB/OL]. [2015-01-10]. https://www.usenix.org/legacy/event/sec11/tech/full_papers/Green.pdf. |
 2016, Vol. 62
2016, Vol. 62





