文章信息
- 郭伟剑, 章泉源, 邓德祥
- GUO Weijian, ZHANG Quanyuan, DENG Dexiang
- 一种车载超短波电台的跳频同步方法
- Hopping Synchronization of Vehicle Ultra-Shortwave Radio
- 武汉大学学报(理学版), 2016, 62(6): 537-541
- Journal of Wuhan University(Natural Science Edition), 2016, 62(6): 537-541
- http://dx.doi.org/10.14188/j.1671-8836.2016.06.008
-
文章历史
- 收稿日期:2015-11-12

2. 上海航天技术研究院, 上海 201109
2. Shanghai Academy of Spaceflight Technology, Shanghai 201109, Shanghai China
跳频(frequency hopping, FH)是一种现代通信常用的扩频方法,即通信双方采用的载波频率同时按同样的规律进行跳变,从时域上扩展了频谱,增强了抗干扰性能.因此基于跳频的通信技术得到了各国广泛的重视,特别是在军事通信领域,例如法国的TRC.950、PR4G,意大利的HYDRAN,以及美军的三大战术通信系统CHESS、SINCGARS和JTIDS[1]. JTIDS更是采用了跳频、直扩和跳时相结合的方法,跳频速率高达76 923 hop/s[2],具有很强的抗干扰能力.
跳频同步是跳频通信的关键技术之一,是跳频通信系统正常工作的必要条件,因此同步的设计至关重要.与一般定点通信电台不同,对于车载超短波跳频电台同步设计要重点考虑:1)电台在无线电静默后的快速入网,要求初始同步时间和迟入网时间短;2)越来越复杂的电磁环境要求同步抗干扰能力要足够的强;3)电台常处于运动状态,电波传输时延不断变化,要求同步保持能力要强.常用的跳频同步方法有独立信道法、同步字头法、自同步法和参考时钟法.比较几种方法,参考时钟法可以实现快速准确的同步,有很高的抗干扰能力[3],除此之外还有迟入网时间短、同步保持时间长、适合高跳速等优点,最符合上述同步设计要求[4].但现有的参考时钟同步法研究都是针对定点通信,若直接用于车载电台跳频同步还存在一些问题.
1 问题分析同步的本质在于使接收方获得与发送方一致的时间起点和时间尺度,参考时钟法的原理就是在接收方和发送方均设置一个准确可靠的时钟,以此时钟作为时间参考,实现接收方与发送方跳频图案的一致[5].
车载电台具有通信距离远、常处于运动状态的特点.参考时钟法用于车载电台时,电波传输时延过大且不确定使得跳频速率降低,并进一步导致同步时间变长以及抗干扰能力下降等问题,具体问题表现在以下几个方面.
1)跳频速率降低.
借助于高精度的参考时钟,系统可以设计非常高的跳速,但由电波传输带来的时延却间接降低了参考时钟精度.以车载超短波电台最大通信距离50 km计算,最大电波传输延迟约为167 μs,对于接收端,跳频图案在时间上滞后了167 μs,按双方跳频图案不超过半跳计算,可支持的最大跳频速率约为6 000 hop/s[5, 6],不能完全体现参考时钟法高跳速的优点.
2)同步时间变长.
参考时钟同步法用于定点跳频通信系统时,电波传输延迟为确定值,理论上不需要粗同步及跟踪过程,同步时间极短甚至为零.用于车载跳频电台时,电波传输延迟不确定,系统需要通过粗同步和跟踪来实现双方跳频图案严格对准.通信双方最大通信距离越长,跳频图案时差越大,同步时间也越长.同时通信双方相对运动速度越快,同步保持能力越低.
3)抗干扰能力降低.
跳频速率的降低,抗干扰能力也随着降低.
本文对所存在的问题进行了分析,在此基础上提出一种基于参考时钟同步法的改进方法,并进行了理论分析和仿真验证.
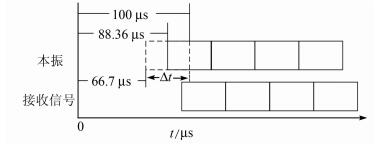
2 同步方案改进及性能分析 2.1 方案改进通信距离太长且不确定是问题产生的根源,距离较短时或通信距离可以确定在一个较小区间内,直接使用延时同步的方法即可获得较高的跳频速率[7].例如,已知双方通信距离在20~30 km之间,电波传输延时Δt在66.7 μs到100 μs之间,接收方跳频图案可预设延迟88.36 μs,如图 1所示,以双方跳频图案时差不超过半跳计算,跳频速率最高可达30 000 hop/s,区间越小跳频速率越高.
|
| 图 1 延时同步 Figure 1 Synchronization by preset delay |
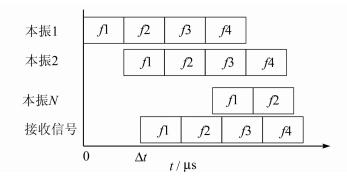
最大通信距离较大时,将其等分为N个连续区间,每个区间预设相应的延时值.设最大通信距离对应的延时为Td,将最大延时等分为N个较小的区间,间隔为Td/N,区间对应的预设延时值为xTd/N,x∈(0,…,N-1).跳频周期为Td/N,跳频速率N/Td,保证至少在某一延时区间的接收信号与本地信号跳频序列差在半跳之内.当通信距离不超过最大通信距离时,必有一支路能够实现同步,如图 2所示,此时最大跳频速率提高为传统方法的N倍.
|
| 图 2 区间延时同步 Figure 2 Synchronization by interval preset delay |
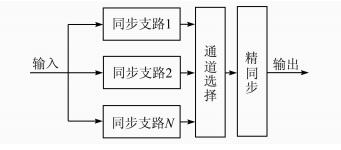
多支路同步结构如图 3所示,由若干个同步支路、通道选择、精同步模块组成[8, 9].
|
| 图 3 多支路并行同步结构图 Figure 3 Multi branch parallel synchronization |
同步支路用于完成信号的相关检测,各支路内部结构相同,仅跳频序列时间上有等差延时,共用跳频器;通道选择模块用于判断哪个支路同步检测值满足条件,并将支路预设延时值转送至精同步模块;精同步模块根据预设延时值进行载波的精确跟踪并完成信号的解调[10].
设延时Δt落入第x个区间,x∈(0,…,N-1),即(x+1)Td/N>Δt>xTd/N.若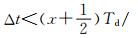
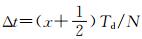
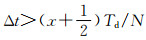
跳频速率:同传统参考时钟法相比,改进方法可以设计更高的跳频速率,通过前面的分析可知,同样的最大通信距离,N条同步支路,理论上跳频速率可提高为传统参考时钟法的N倍.
初始同步时间:设检测长度为M,同样的最大通信距离,由于跳频周期缩短,初始同步时间也缩短.不考虑噪声影响的情况下,改进方案的同步时间为MTd/N,而传统参考时钟法为MTd.
检测概率、虚检概率:本方案采取的是并行多支路同步方法,因此先计算单支路的检测概率和虚检概率,单支路的计算方法同传统参考时钟法相同.
单支路情况下,设检测概率为PD,虚检概率为PFA.高斯白噪声信道下,检测在跳频信号解跳后进行,其计算方法与传统的滑动相关法相同.对于中频滤波器输出端,第i跳,输入波形可用窄带波形表示[11, 12]:
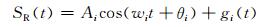
|
其中,SR(t)为接收信号,Ai为信号幅度,wi为由跳频序列决定的角频率,gi(t)是方差为σ2的高斯过程.
计算得:
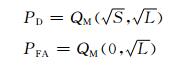
|
其中,QM是(Marcum’s)Q函数,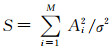
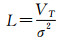
多支路情况下,设检测概率为P′D,虚检测概率为P′FA,其中一支路正确检测,其余支路未虚检,则系统正确检测;任一支路发生虚检,则系统发生虚检.因此系统检测概率[13]:
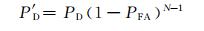
|
虚检概率:
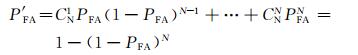
|
恒虚检概率下,支路数和检测长度是影响系统检测概率的主要因素.
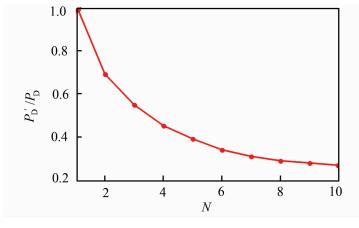
3 支路数和检测长度对检测概率的影响 3.1 支路数的影响支路数的选取要对跳频速率和检测概率两个因素进行综合考虑. N太小跳频速率的提高有限,太大会导致检测概率过度降低.仿真设置虚检概率为1.0×10-3,信噪比SNR=3 dB,检测长度M=1,N与检测概率PD的关系如图 4所示.
|
| 图 4 支路数对检测概率比值的影响 Figure 4 Influence of branch number on the ratio of detection probability |
从图 4中可以看出,随着支路数的增加,系统检测概率有所降低,这是由于采用多支路同步,系统发生虚检的概率增加,导致检测概率降低.支路数在1~4之间,检测概率变化较快,支路数超过5后,变化逐渐趋于平缓. N的选取在满足跳频速率要求的基础上应尽量取小,同时由多支路引起的检测概率降低可以通过适当增加检测长度M来弥补,甚至提高.
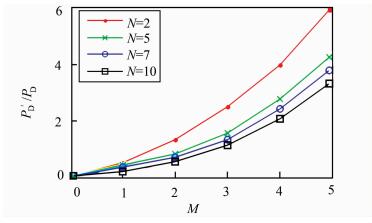
3.2 检测长度的影响检测长度的选取要对检测概率和同步时间进行综合考虑.仿真设置虚检概率为1.0×10-3,信噪比SNR=3 dB,传统方法检测长度M=1,支路数N取2,5,7,10的情况下.同步时间与检测长度成正比关系,检测概率变化与检测长度的关系如图 5所示.
|
| 图 5 检测长度对检测概率比值的影响 Figure 5 Influence of detection length on the ratio of detection probability |
从图 5中可知,随着M的增加,检测概率逐渐增加,支路数越大增速越小.具体设计时,根据支路数的数量,选择合适的M值保证检测时间缩短的同时提高检测概率.
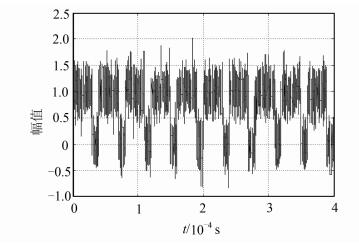
4 仿真利用Matlab在加性高斯白噪声环境下进行仿真验证[14],最大通信距离50 km,最大传输时延Td=167 μs,支路数N=5,预设延时值分别为0,37.1,74.2,111.3,148.4 μs,跳频速率为25 000 hop/s,频点为5个[15],通信延迟10 μs.信号经过混频、滤波和检波后,预设延时值为0 μs,支路输出如图 6所示.在未同步时差内波形有明显突变,正确同步时长超过半跳,实现粗同步.其他支路输出均值为0的噪声信号,未能实现同步.
|
| 图 6 包络检波输出 Figure 6 Output by envelope detector |
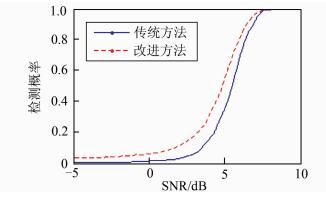
在恒虚检概率为1.0×10-3情况下,传统方法M=1,改进方法M=3,对检测概率进行仿真对比,结果如图 7所示.信噪比为0~7 dB之间的改进方法检测概率相对于传统参考时钟法有明显提高,信噪比为8 dB时两种方法都达到理想检测性能,改进方法有效提高了系统抗干扰能力.传统方法跳频速率6 000 hop/s,检测长度M=1.改进方法跳频速率25 000 hop/s,检测长度M=3.计算可得,改进方法同步时间缩短28%.
|
| 图 7 检测概率对比 Figure 7 Comparison of detection probability |
对传统参考时钟法直接用于车载超短波电台跳频同步存在的问题进行了分析,结合超短波电台通信的特点提出一种多支路并行同步的改进方法,并对支路数和检测长度对检测概率的影响进行了量化分析.最后利用Matlab对系统进行了仿真验证,跳频速率由6 000 hop/s提高到25 000 hop/s, 同步时间缩短28%.结果表明,改进方法能够有效提高跳频速率、缩短同步时间、提高检测概率以及增强抗干扰能力,更加符合车载超短波电台跳频同步设计要求,对未来车载超短波电台跳频设计有一定有参考价值.
| [1] | 梅文华. 跳频通信.[M] 北京: 国防工业出版社, 2005 : 150 -162. MEI W H. Frequency Hopping Communication.[M] Beijing: Publishing House of National Defense Industry, 2005 : 150 -162. |
| [2] | 刘璇, 赤县. JTIDS混合扩频信号的研究与实现[J]. 战术导弹技术 , 2007 (2) : 41–46 LIU X, CHI X. Research and realization of hybrid spread spectrum communication signal in JITDS[J]. Tactical Missile Technology , 2007 (2) : 41–46 |
| [3] | 赵东阳.基于北斗导航系统的跳频同步研究[D].西安:西安电子科技大学, 2008. ZHAO D Y. The Study of Frequency-hopping Synchronization Based on Beidou Navigation System [D]. Xi'an:Xidian University, 2008(Ch). http://cdmd.cnki.com.cn/Article/CDMD-10701-2008056247.htm |
| [4] | 何苏勤, 张海庆. 组网跳频电台同步过程的设计及实现[J]. 计算机工程与设计 , 2011, 32 (9) : 2961–2965 HE S Q, ZHANG H Q. Design and implementation of building-net frequency hopping system synchronization process[J]. Computer Engineering and Design , 2011, 32 (9) : 2961–2965 |
| [5] | 毛席龙, 毛善国. 基于北斗无源授时的战术电台同步技术研究[J]. 现代电子技术 , 2007 (3) : 14–17 MAO X L, MAO S G. Research of tactics radio synchronization technique based on beidou passive timing[J]. Modern Electronic Technique , 2007 (3) : 14–17 |
| [6] | 胡汉武, 赵峙岳. 一种基于北斗授时的跳频同步方法实现[J]. 国外电子测量技术 , 2013, 32 (8) : 10–14 HU H W, ZHAO S Y. Frequency hopping synchronization method based on beidou timing[J]. Foreign Electronic Measurement Technology , 2013, 32 (8) : 10–14 |
| [7] | 金红军. 超短波远距离山区通信关键技术研究[J]. 通信技术 , 2013, 46 (258) : 22–25 JIN H J. Key technologies of ultra-short wave long-distance mountain communication[J]. Communication Technology , 2013, 46 (258) : 22–25 |
| [8] | 谢宇. 一种多信道跳频通信系统信道控制方法[J]. 通信技术 , 2014, 47 (8) : 915–918 XIE Y. A method of channel assignment for multi-channel frequency-hopping communication system[J]. Communication Technology , 2014, 47 (8) : 915–918 |
| [9] | YU N, QI X H, QIAO X L. Multi-channels wideband digital reconnaissance receiver based on compressed sensing[J]. Signal Processing , 2013, 7 (8) : 731–742 |
| [10] | SULTANOV B, RUMYANTSEVA N, ZEFIROV S. Analysis of the fast acquisition method in frequency hopping systems[J]. Journal of Communications Technology and Electronics , 2013, 58 (7) : 526–565 |
| [11] | 赵花荣, 赵明生, 罗康生. 具有强抗干扰性的快速跳频捕获方案设计[J]. 清华大学学报(自然科学版) , 2007, 47 (4) : 546–560 ZHAO H R, ZHAO M S, LUO K S. Fast acquisition scheme with excellent anti-jamming performance[J]. Journal of Tsinghua University (Science and Technology) , 2007, 47 (4) : 546–560 |
| [12] | CHEN X F, HARRIS F, VENOSA E. Polyphase channelizers for fully digital frequency hopping systems[J]. Analog Integrated Circuits and Signal Processing , 2012, 73 (2) : 517–530 DOI:10.1007/s10470-012-9926-4 |
| [13] | 窦秀娟.基于simulink的跳频同步技术仿真平台的设计与实现[D].成都:电子科技大学, 2013. DOU X J. Design and Implementation of Simulation Platform for Frequency Hopping Synchronization Method Based on Simulink [D]. Chengdu:University of Electronic Science and Technology of China, 2013(Ch). http://cdmd.cnki.com.cn/Article/CDMD-10614-1013329053.htm |
| [14] | 刘颖, 张天辉, 袁丁, 等. 跳频通信系统设计与仿真实现[J]. 通信技术 , 2013, 46 (10) : 18–21 LIU Y, ZHANG T H, YUAN D, et al. Design and simulation of FH communication system[J]. Communication Technology , 2013, 46 (10) : 18–21 |
| [15] | ZENG X Y, CAI H, TANG X H. A class of optimal frequency hopping sequences with new parameters[J]. Information Theory , 2013, 58 (7) : 4899–4907 |
 2016, Vol. 62
2016, Vol. 62





