0 引 言

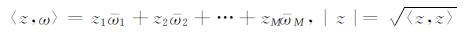
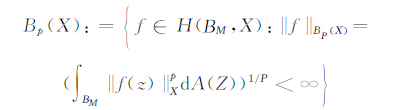
对于给定的正整数M,设C^M是M维的复空间,将C^M上的单位开球记为B_M,其边界及为B_M. 对z=(z₁,z₂,…,z_M),ω=(ω₁,ω₂,…ωM)∈C^M,记设H(B_M)是B_M上解析函数全体,dA表示B_M上规范化的体积测度,即A(B_M)=1．设(X,〈·,·〉X)是可分的Hilbert空间,则H(B_M,X)是定义在B_M上且取值于X的解析函数全体．当1≤p<∞时,向量值Bergman空间B_p(X）的定义为

易证B_P(X)(1≤P<∞)是Banach空间．且B₂(X)是Hilbert空间,其内积为

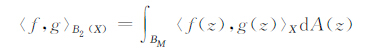
若X=C,则B_p:=B_p(C)即为球上的标量值Bergman空间．若φ是B_M到自身的解析映射,则其复合算子定义为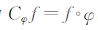,其中f∈H(B_M,X).显然Cφ是H(B_M,X)到自身的线性算子．关于各种空间上的复合算子得到了广泛研究,相关结论可参考文献^[1~4].特别地,当φ和ψ是C内单位圆盘D到自身的线性分式变换时,文献^[5]研究了向量值Bergman空间B₁(X)上的算子CφC^*ψ和C^*ψCφ的弱紧性．本文的主要工作就是将文献^[5]中的结论推广到多维情形．

为了叙述方便,后文中,总假设(X,〈·,·〉X)是可分的Hilbert空间.

1 准备知识

为了得到B₂(X)中的核函数,下面先给出下述估计. 引理1 如果1≤P<∞并且f∈B_p(X)，则存在一个正常数C使得

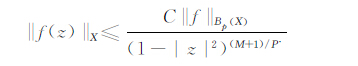
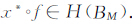
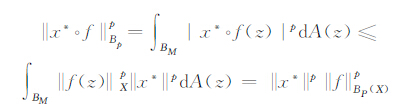
证 若x^*∈X^*,则显然x^*οf∈H(B_M).又因为

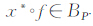
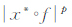
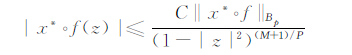
所以.由的次调和性知

则

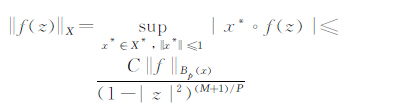
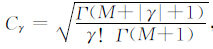
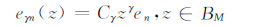
对下文中出现的记号做如下约定.对于M元非负整数组γ=(γ₁…,γ_M)和z=(z₁,…,z_M)∈B_M,记z^γ=z^γ1₁…z^γM_M.若设,则{C_γz^γ}就构成了B₂的一个标准正交基(见文献^[6]).取X的标准正交基为{e_n:n∈N},其中N={0,1,2,…}.现在定义e_γn:B_M→X为

则下述引理成立．

引理2 {e_γn}是B₂(X)的一个标准正交基．

证 对于M元非负整数组α与γ和n,m∈N,有

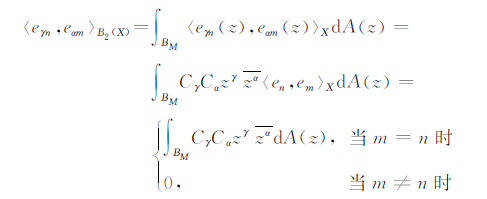
注意到

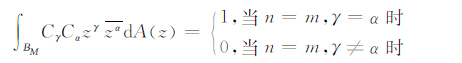
从而{e_γn}是B₂(X)的一个标准正交集.下证{e_γn}是B₂(X)的一个基.为此,设f∈B₂(X)使得

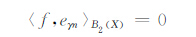
对所有的γ和n都成立,即

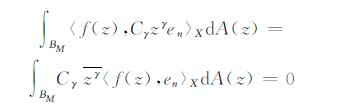
因为{C_γz^γ}是B₂的一个标准正交基,所以

又{e_n}是X的一个标准正交基,故f≡0.从而{e_γn}是B₂(X)的一个标准正交基．

令E^j_z(f)=〈f(z),e_j〉_X,其中z∈B_M,j∈N,f∈B₂(X).由引理1知E^j_z是B₂(X)上的一个有界线性泛函,则由Riesz表示定理可知,存在E^j_z∈B₂(X)使得

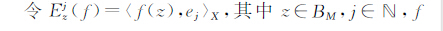
对所有的f∈B₂(X)均成立.此时称K^j_z为向量值Bergman核函数,并且它有下述明确表达式.

引理3 对于z∈B_M和j∈N,向量值Bergman核函数为

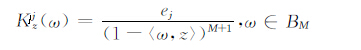
证 由引理2知{e_γn}是B₂(X)的一个标准正交基,因此

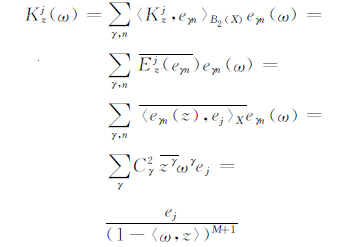
由引理3,可知‖K^j_z‖B₂(X)=(1－|z|²)^－(M+1)/2.

引理4 Span {K^j_z}在B₂(X)中稠密.

证 设f∈B₂(X).若对任意的z∈B_M和j∈N均有〈f,K^j_z〉B₂(X)=0,即〈f(z),e_j〉X=0.由于{e_j}是X的标准正交基,故f≡0.因此Span{K^j_z}在B₂(X)中稠密.

设L^p(B_M,X)(1≤p<∞)是定义在B_M上且取值于X的并满足

的可测函数全体.

引理5 若P是从(L²B_M,X)到B₂(X)的正交投影算子,则对所有的f∈L²(B_M,X),均有

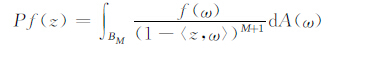
证 因为{e_γn}是B₂(X)的一个标准正交基,所以对任一f∈L²(B_M,X),有

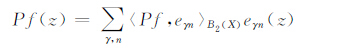
注意到

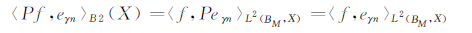
所以

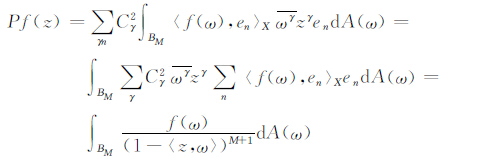
由于固定z∈B_M后在ω∈B_M中是一致收敛的，故第二个等式成立.从而引理得证.

尽管P定义在L²(B_M,X)上,但是可以将其延拓至L¹(B_M,X)上(考虑函数f(rz),r∈(0,1),令r→1),若f∈B₂(X),则Pf=f.因为B₂(X)在B₁(X)中稠密,则下述结论成立.

引理6 若f∈B₁(X),则

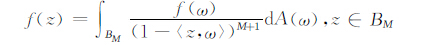
并且该积分在B_M的任一紧子集上按B₁(X)的范数一致收敛.

对于β≥0和f∈B₁(X),类似地有

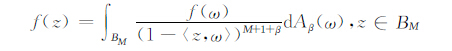
其中dA_β(ω)=c_β(1－|ω|²)^βdA(ω),A_β(B_M)=1且c_β=Γ(M+β+1)/(M!Γ(β+1)).

对任意的z∈B_M,设φz是交换0和z的对合自同构.记H(B_M,X)中的函数f的梯度为

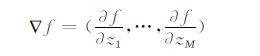
此时,向量值Bloch空间B(X)定义为

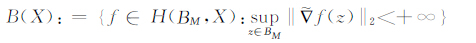
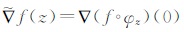
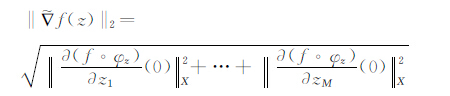
其中,且

进一步地,小Bloch空间B₀(X)为

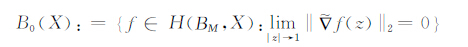
若在以上两空间上定义范数

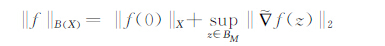
则Bloch空间B(X)是Banach空间,并且B₀(X)是B(X)的闭子空间.容易验证

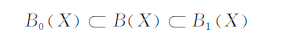
从引理1知,Bergman空间B₁(X)有非平凡的有界线性泛函.令B₁(X)^*表示B₁(X)的共轭空间,则有以下引理.

引理7 在对偶形式

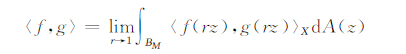
下有B₀(X)^*=B₁(X),并且B₁(X)^*=B(X)（在等价范数意义下）.

此引理的证明与文献^[6]中定理3.16和3.17的证明类似,此处略去.

对于g∈L∞(B_M),定义B₁(X)上的Toeplitz算子为

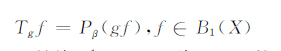
其中β>0,P_β是从L¹(B_M,X)到B₁(X)的有界投影算子:

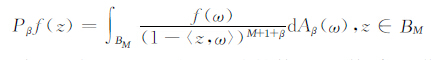
由定义可知T_g是一个有界线性算子.且特别地,若g∈H^∞(B_M)(B_M上的有界解析函数全体),则T_g在B₀(X),B(X)和B₁(X)上均为有界线性算子,根据Hahn-Banach定理,可设T^*g定义在B₁(X)上,且T^*g=T_g,T_hT_g=Thg,T_gT_h=T_gh.

由文献^[7]可知,只要φ是B_M到自身的线性分式变换,Cφ在标量值Bergman空间B₂上就有界.再由文献^[8]的类似讨论可知,Cφ在向量值Bergman空间B₂(X)上也有界.又因为B₂(X)在B₁(X)中稠密,所以Cφ可保范延拓到B₁(X)上.另外,也易证Cφ也是B(X)和B₀(X)上的有界线性算子.

引理8 若φ(z)=(Az+B)(〈z,C〉+D)－1是B_M到自身的线性分式变换,其中B,C∈C^M,D∈C且A为M×M的复矩阵,则σ(z)=(A^*z－C)(〈z,－B〉+D^*)－1也是B_M到自身的线性分式变换,函数g(z)=(〈z,－B〉+D^*)^－(M+1)和h(z)=(〈z,C〉+D)^M+1都在H^∞(B_M)中,且

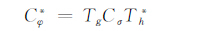
(1)

在B₁(X)上成立.

证 由文献^[7]可知,只需证明C^*φ=T_gCσT^*h在B₁(X)上成立即可．且由Hahn-Banach定理知,公式(1)的两边在B₁(X)上的定义均合理,对于ω∈B_M和j∈N,设

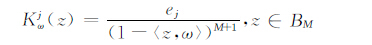
其中{e_j}是X的标准正交基.显然T^*hK^j_ω=h(ω)K^j_ω和C^*_φK^j_ω=K^j_φ(ω).因此

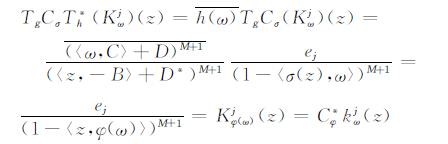
由于B₂(X)在B₁(X)中稠密,并且Span{K^j_ω,ω∈B_M,j∈N}是B₂(X)的稠密子集,所以要证的等式(1)成立.

若设g₁(z)=(〈z,C〉+D)^－(M+1),h₁(z)=(〈z,－B〉+D^*)^M+1,同理可得

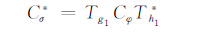
(2)

事实上,φ和σ还有以下性质;

(P1) 若η∈B_M,φ(η)=ω∈B_M,则σ(ω)=η.

(P2) 若ω∈B_M,σ(ω)=η∈B_M,则φ(η)=ω.

与φ,

类似的,可以考虑另一对分式线性变换ψ,且满足

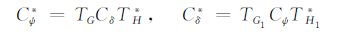
(3)

其中G,H,G₁,H₁的定义分别与g,h,g₁,h₁类似.

引理9 若φ,ψ是B_M到自身的分式线性变换,则CφC^*ψ在B₁(X)上弱紧当且仅当CφC_δ在B₁(X)上弱紧.

证 若CφC^*ψ在B₁(X)上弱紧,则由(3)式知

故CφC_δ在B₁(X)中弱紧. 反之,若CφC_δ在B₁(X)上弱紧,则由(3)式知

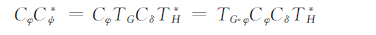
故CφC^*ψ在B₁(X)上弱紧.

引理10 若φ和ψ是B_M到自身的可逆分式线性变换,则C^*ψCφ在B₁(X)上弱紧当且仅当C_δCφ在B₁(X)上弱紧.

证 若C^*ψCφ在B₁(X)上弱紧,则由(3)式知

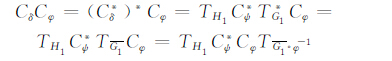
又G₁οφ^－1∈H^∞(B_M),则C_δCφ在B₁(X)上弱紧.

反之,若C_δCφ在B₁(X)上弱紧,则由引理9知C_δC^*_σ也在B₁(X)上弱紧.又因为

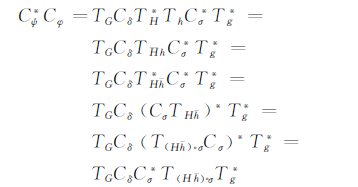
所以C^*ψCφ在B₁(X)上弱紧.

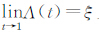
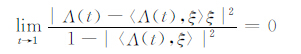
为了刻画CφC^*ψ和C^*ψCφ的弱紧性,需要引入角导数的概念.对ξ∈B_M,称连续函数Λ(t):［0,1)→B_M为限制ξ-曲线,若且

和

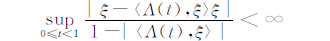
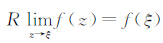
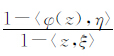
称f:B_M→C在ξ处存在限制极限,并记此极限为f(ξ),若当t→1时,f(Λ(t))沿着任意的限制ξ-曲线Λ(t)均趋于f(ξ).此时,记为.称解析自映射φ:B_M→B_M在ξ处存在有限角导数,并记为Aφ(ξ),若存在η∈B_M使得在ξ处存在限制极限,即

易知若φ在ξ处存在有限角导数,则φ在ξ处必存在限制极限且φ(ξ)=η.参考文献^[9]可得如下引理.

引理11 若φ是B_M到自身的分式线性变换,则Cφ在B₁(X)上弱紧当且仅当φ在B_M上没有有限角导数.

由此引理很容易得到下述推论.

推论1 若φ是B_M到自身的分式线性变换,则Cφ在B₁(X)中弱紧当且仅当φ映B_M到B_M.

2 主要结论

下面我们来阐述并证明本文的主要结论.

定理1 若φ和ψ是B_M到自身的分式线性交换,则CφC^*ψ在B₁(X)上非弱紧当且仅当存在η1,η2∈B_M使得φ(η1)=ψ(η2)∈∂B_M.

证 由引理9知CφC^*ψ在B₁(X)上非弱紧当且仅当CφC_δ=C_δοφ在B₁(X)上非弱紧．又δοφ是B_M到自身的分式线性变换,由推论1知,C_δοφ是非弱紧的当且仅当存在η1,η2∈B_M使得δοφ(η1)=η2.则由(P2)知存在ζ∈B_M使得φ(η1)=ψ(η1)=ζ,得证.

由角导数的定义,有如下的推论.

推论2 若φ和ψ是B_M到自身的可逆分式线性变换,则CφC^*ψ在B₁(X)上非弱紧当且仅当存在ω∈B_M,使得φ和ψ在φ^－1(ω),ψ^－1(ω)∈B_M上有有限角导数.

定理2 若φ和ψ是B_M到自身的可逆分式线性变换,则C^*ψCφ在B₁(X)上非弱紧当且仅当存在ω₁,ω₂∈B_M,使得∂φ^－1(ω₁)=ψ^－1(ω₂)∈∂B_M.

证 由引理10知C^*ψCφ在B₁(X)上非弱紧当且仅当C_δCφ=Cφοδ在B₁(X)上非弱紧.又φοδ是B_M到自身的分式线性变换,由推论1知Cφοδ在B₁(X)上非弱紧等价于存在ω₁,ω₂∈B_M,使得φοδ(ω₂)=ω₁,由(P1)知,存在η∈B_M,使得σ(ω₁)=δ(ω₂)=η.因此φ(η)=ω₁,ψ(η)=ω₂,则φ－1(ω₁)=ψ－1(ω₂)=η∈B_M,得证.

推论3 若φ和ψ是B_M到自身的可逆分式线性变换,则C^*ψCφ在B₁(X)上非弱紧当且仅当φ和ψ在B_M中的某一点处都有有限角导数.

例1 CφC^*ψ在B₁(X)上弱紧,但C^*ψCφ非弱紧,其中

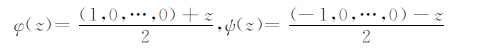
证 令φ(ω)=ψ(η),ω,η∈B_M，则ω₁+η1=－2.从而|1－(－ω₁〖TX-〗η1)|=2,则ω₁η₁=1.所以必有|ω₁|=|η1|=1和ω₁=η1.从而ω=η,由定理1知CφC^*ψ在B₁(X)上弱紧.

另一方面,显然有φ－1(ω)=2ω－(1,0,…,0)且ψ－1(η)=－2η－(1,0,…,0).取B_M中的两个不同点ω=(1,0,…,0)和η=－(1,0,…,0)，则φ－1(ω)=ψ－1(η).从而由定理2知C^*ψCφ在B₁(X)上非弱紧.

以下两例的证明与例1证明类似.

例2 CφC^*ψ在B₁(X)上非弱紧,但C^*ψCφ弱紧,其中

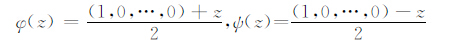
例3 CφC^*ψ与C^*ψCφ在B₁(X)上都弱紧,其中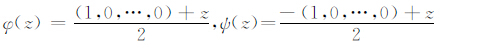

以上3个例子说明C^*ψCφ和CφC^*ψ在B₁(X)上弱紧的差异.