文章信息
- 林英, 谢勇, 朱艳萍, 康雁
- LIN Ying, XIE Yong, ZHU Yanping, KANG Yan
- 基于空间四分的Hilbert位置k-匿名算法设计与实现
- The Design and Implement of Hilbert Location k-Anonymity Algorithm Based on Spatial Quadtree
- 武汉大学学报(理学版), 2018, 64(3): 225-230
- Journal of Wuhan University(Natural Science Edition), 2018, 64(3): 225-230
- http://dx.doi.org/10.14188/j.1671-8836.2018.03.004
-
文章历史
- 收稿日期:2017-06-03

目前,各种各样基于位置的服务(location-based services, LBS)层出不穷,人们可以通过发送自己的当前位置,获取周边的相关服务,如寻找附近的医院、饭店、商场等.LBS极大方便了人们的日常生活,但使用该服务也意味着个人位置信息的公开,如去过何地、做过何事,个人隐私和安全受到了很大的威胁.面对位置服务的一系列问题,隐私保护是位置服务研究者们致力解决的重要问题.
位置隐私保护研究面对的核心问题是保护隐私与服务质量之间的矛盾[1].也就是用户需要通过公布位置信息来获取LBS,使用越准确的位置信息,就能收到更好的服务反馈,然而,由于受到保护位置隐私的制约,服务质量往往会受到影响.对于位置匿名化来说,平衡这两方面的关系是很难的,但又是必须要考虑的.目前众多研究者都在想办法在这两方面寻找平衡,即在保证位置隐私的前提下,使用户获得更好的服务体验.
1 相关工作 1.1 位置k-匿名算法位置匿名通过空间隐匿来实现,其研究焦点是使隐匿区域尽量小,以保证服务质量[1].位置k-匿名(location k-anonymity)技术的思想在2003年首次由Gruteser等[2]提出,它是使用一块包含至少k个不可区分位置的匿名区域代替真实位置,从而在一定程度上保护用户位置信息.他们同时还提出了一种基于空间四分的间隔匿名算法(interval cloak)[2].基于空间四分法寻找匿名区域的基础是不断通过空间四分方法缩小或者扩大空间区域,最终寻找到符合k-匿名要求的区域.间隔匿名算法在实现时,采取了自底向上的方式进行匿名区域搜索,当底层区域不满足k-匿名要求时,向上一层扩张,不断重复,直到寻找到某个区域中用户大于或等于k则返回该区域.该算法简单速度快,但是其每次扩张的区域较大,使得最终得到的匿名区域会比较大,包含的位置数据也比较多,其数量会远大于要求的k值.间隔匿名方法虽然有着更好的隐私性,可是却大大降低了服务的准确性,所以在保证满足k值匿名要求的前提下,可以通过优化缩小匿名区域的方法,以达到更加接近隐私和服务平衡的目标.
2006年,出现了Casper匿名法(Casper cloak)[3],Casper匿名算法也是一种基于空间四分的匿名算法,该方法改进了间隔匿名法的扫描过程,相比之下能够得出更小的匿名区域.在寻找匿名区域时,Casper算法不是像间隔匿名法,每次扩展时都直接扩展到上层的父区域,而是在底层区域没有达到k-匿名要求时,先判断相邻的两个兄弟区域与它组合时包含的对象数是不是符合k值.若符合则该组合区作为匿名区域,若不符合再向上搜索上层父区域.这样通过减小每次搜索扩展的单位面积,可以获取更小的匿名面积,通过改进间隔匿名法使得出的匿名空间更优.
2007年,Hilbert匿名法(Hilbert cloak)[4]出现.Hilbert匿名法是基于Hilbert填充曲线(Hilbert Curve)的.通过Hilbert曲线可以将平面上的二维坐标转换为一个Hilbert编码值,相邻的Hilbert值对应在二维空间上也有很大概率相邻,又可以将其组合成一个区域.Hilbert匿名法利用这一特性,将二维空间上的坐标转化为对应的Hilbert值,再按照顺序将值进行排列,进行k-匿名时,将相邻值代表的坐标点放在一起,共同构成匿名框.
位置k-匿名算法的改进常常在以上几种方法的基础上进行.近年来,出现了许多以减小匿名空间为目标的研究,如文献[5]利用网格划分和不同的搜索扩张方式,在满足匿名要求的前提下,得到了更小的匿名区域;文献[6]针对网格划分空间位置匿名算法在用户分布较稀疏或k值较大时存在产生的匿名空间区域过大和匿名成功率较低从而导致服务质量下降的问题,采用引入最大匿名区间和最长可容忍时间参数的方法,通过参数限制匿名区域的大小以及服务延迟的时间,形成满足条件的较小匿名区域;文献[7]针对空间划分精度太粗导致空间产生冗余而过大的问题,引入基于网格和密度的方法,以减小匿名空间.
1.2 位置隐私保护体系结构位置隐私保护体系结构主要是三种:中心式、独立式和分布式点对点结构[8].独立式结构即Client-Server架构,在该结构下,隐私保护由用户进行,用户将匿名化后的信息传给位置服务商,待位置服务商返回结果后,用户再进行过滤获取有效信息.分布式点对点结构通过各个用户之间合作来进行隐私保护操作,在该结构下,邻近的各个节点进行协作,共同得出一个匿名区域发送给位置服务商,待得到返回结果后再对信息过滤获取有效信息.本文主要考虑的是中心式结构下匿名处理的方法.
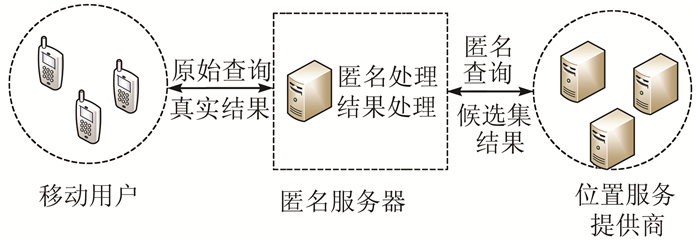
中心式结构在用户和服务商中间有可信第三方.中心服务器集中收集发起请求的所在地点,然后将精确信息匿名化,使用匿名化的信息请求位置服务,待得到返回结果之后,再将结果求精返回给用户.图 1是中心式结构的体系结构图,该结构可避免位置服务提供商不安全的问题,集中处理可获得更多的待选数据,使得匿名更容易实现.但该结构不足之处在于中心服务器负担较繁重,会产生瓶颈,另外如果中心服务器被攻破,大量的隐私信息会被泄露[8].
|
| 图 1 中心式结构 Figure 1 Third trusted party architecture |
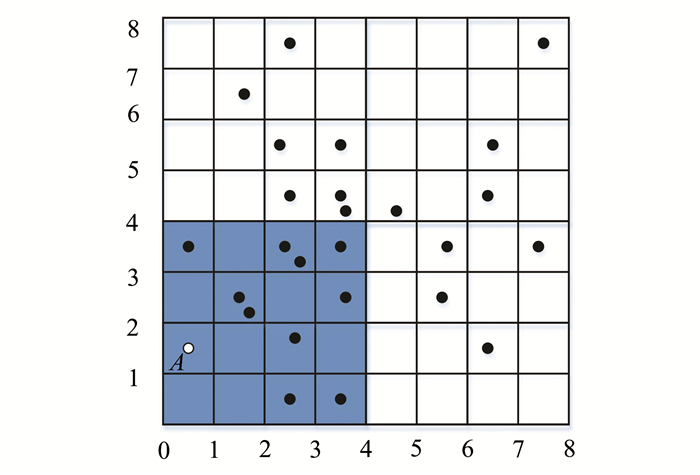
基于空间四分的位置k-匿名法比较简单,理解起来也很容易,并且根据四叉树结构索引自底向上搜索,能够很快得到匿名区域.但是其每次扩张的区域较大,使得最终得到的匿名区域会比较大,包含的位置数据也比较多,会远大于要求的k值.这种情况下,虽然有着更好的隐私性,可是却大大降低了服务的准确性,所以在保证满足k值匿名要求的前提下,可以缩小匿名区域,以更好地达到隐私和服务的平衡.如图 2,颜色较深区域是k=4时使用基于空间四分k-匿名法得到的A的匿名框.A要求k值为4,先搜索到父区域([0, 0], [2, 2]),不符合k值,则扩展到上层父区域([0, 0], [4, 4]),最终得到了符合k-匿名要求的区域([0, 0], [4, 4]).可以看到匿名区域中存在11个对象,远远大于k=4的要求.
|
| 图 2 空间四分k-匿名法的匿名区域 Figure 2 Spatial quadtree k-anonymity cloaking area |
基于Hilbert曲线的匿名方法因为Hilbert曲线的特性,能够集聚空间上的对象,使得沿着曲线的区域在空间上较为邻近,另外Hilbert曲线还有一个重要优点是可以把多维转换成一维.但是使用基于Hilbert曲线的匿名方法在位置对象分布稀疏、整体背景区域大的情况下获得的匿名区域也会比较大.
本文的研究目的是在能够满足k-匿名要求的情况下,减小匿名区域的大小.本文尝试将基于空间的四分法和基于Hilbert曲线的方法结合使用,在基于空间四分法得出的包含对象数超过k值过多的匿名区域之上,再利用Hilbert曲线的特点进行优化,以得出包含对象数更接近于k值,且匿名面积更小的区域.
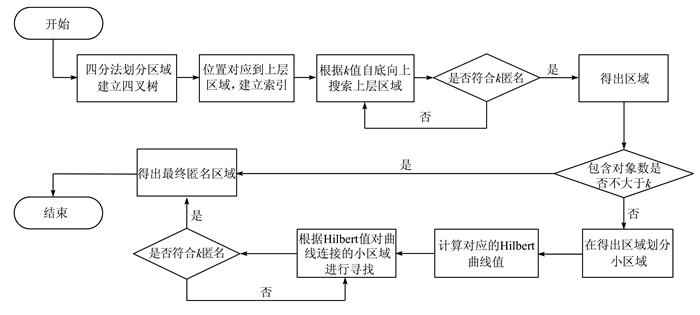
2.2 算法描述首先利用空间四分法合理划分区域,从最下层向上扩展,得出符合k值要求的区域,然后将该区域所包含的对象数与k值进行比较,若超过k值,则在该区域使用Hilbert曲线法,根据包含对象数量,划分出满足2n×2n且大于原区域包含对象数的小区域,转换为Hilbert曲线值,以该值为序,搜索邻近区域,最后得出新的匿名区域.图 3是该方法的主要流程图,其主要过程如下:
|
| 图 3 空间四分及Hilbert结合匿名法流程图 Figure 3 Flow chart of Spatial Quadtree & Hilbert anonymity method |
步骤1 对区域进行逐层空间四分,并建立类四叉树的结构,将已有的位置数据对应到各个区域.
步骤2 根据k值大小要求,从对应的最底层开始,自底向上搜索符合要求的匿名区域,搜索时按照间隔匿名法原理,每次向上扩展到父区域.
步骤3 如果得出的匿名区域中包含的匿名对象数大于k,表示可优化,则继续进行下一步;如果得出的区域中匿名对象数直接符合k,则直接跳到最后一步.
步骤4 在该区域上根据其中的匿名对象数进行四分,使划分出的网格数大于或等于该小区域中的匿名对象数.
步骤5 根据Hilbert曲线对上一步得到的网格进行编码,剔除未包含任何对象的空网格并根据顺序排列.
步骤6 按照Hilbert曲线得出的编码进行搜索,如果匿名发起对象对应中间编码则首先向前搜索,再向后搜索;如果位置匿名发起对象对应开头编码或是向前搜索到开始编码,则一直向后搜索;如果位置匿名发起对象对应结尾编码或是向后搜索到结尾编码,则一直向前搜索.不断重复以上步骤,直到已搜索网格中包含的匿名对象满足k值要求.
步骤7 得出满足k值要求的矩形区域作为保护发起者位置的匿名区域.
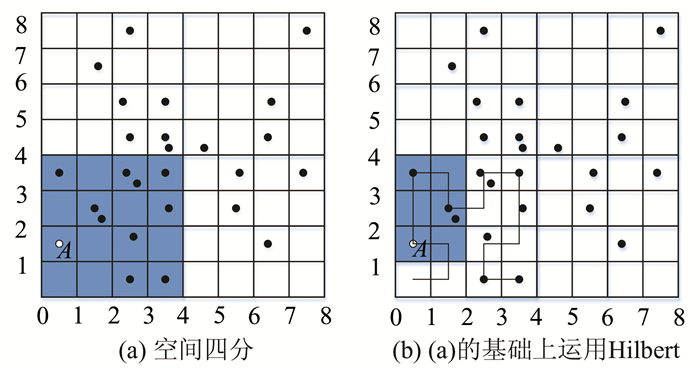
接下来以一个例子来描述该方法,如图 4所示.A提出k=4的匿名要求,于是首先根据间隔匿名法的原理,从四叉树最底层开始搜索,搜索顺序是([0, 1], [1, 2])→([0, 0], [2, 2])→([0, 0], [4, 4]),得出匿名区域为([0, 0], [4, 4]),如图 4(a)阴影部分.在该区域中包含11个匿名对象,大于k=4的要求.所以在该区域上使用Hilbert匿名法进行优化,在该区域上划分出16个小的网格,并根据Hilbert曲线进行搜索,最终得到的匿名区域为([0, 1], [2, 4]),如图 4(b)阴影部分,使用该片区域作为A的位置匿名区域.对比之前的匿名区域,新区域面积减小,且包含的对象数也更加符合k值要求.在保证达到k-匿名要求的同时,获得了更小的匿名区域,在平衡隐私与服务上取得了更理想的结果.
|
| 图 4 基于空间四分和Hilbert曲线的位置匿名法示意图 Figure 4 Spatial Quadtree & Hilbert based location anonymity method |
算法使用C语言实现,编译环境为Visual Studio 2017 RC,在处理器AMD A8-5550M 2.1 GHz、内存为4 GB、操作系统为Windows 10专业版的平台上运行.实验数据采用的是Brinkhoff移动对象生成器生成的数据.为了测试位置对象数量的多少是否会影响匿名区域大小,本次实验生成了两组数据,分别包含1 184和409条数据,以模拟在同一个背景区域下,位置对象分布稠密及稀疏的情况.实验得出的结果是为每一个位置坐标寻找匿名区域后计算得出的平均值,k值的选择为5~20.由于本文尝试的方法是基于空间四分和Hilbert曲线的,所以最后的实验结果和间隔匿名法(IC)、Casper匿名法、Hilbert匿名法等其他3种k-匿名方法进行了对比.Quad-h为本文提出方法.
首先进行的是匿名区域大小测试.匿名区域(cloaking region)是经过处理过程后得出的匿名框的面积大小[9].匿名区域面积是位置隐私匿名保护一个重要的评价标准之一,主要反映服务质量,因为较小面积的匿名区域在进行位置服务查询时能够获得较准确的查询,同时带来较低的查询代价.本文实验测试得到的有关匿名区域面积的结果如表 1(1 184条数据)和表 2(409条数据)所示.取不同k值进行实验,从实验结果可以看出,本文的方法由于基于间隔匿名法进行改进,因此得到的匿名区域与之相比有了大幅度减小;而与Casper和Hilbert两种匿名法相比,本文方法得出的匿名区域也较小,而且也可以看出,匿名区域在位置对象分布稀疏时要大于分布稠密的情况,这也符合实际情况.
| k值 | IC | Casper | Hilbert | Quad-h |
| 5 | 30 | 14 | 15 | 10 |
| 7 | 45 | 21 | 25 | 16 |
| 9 | 64 | 29 | 32 | 22 |
| 11 | 80 | 36 | 41 | 27 |
| 13 | 88 | 42 | 51 | 36 |
| 15 | 111 | 51 | 59 | 47 |
| 17 | 140 | 63 | 70 | 51 |
| 19 | 166 | 78 | 79 | 60 |
| k值 | IC | Casper | Hilbert | Quad-h |
| 5 | 83 | 33 | 36 | 26 |
| 7 | 104 | 49 | 59 | 47 |
| 9 | 157 | 79 | 87 | 73 |
| 11 | 281 | 115 | 114 | 93 |
| 13 | 370 | 143 | 145 | 113 |
| 15 | 405 | 161 | 173 | 138 |
| 17 | 494 | 191 | 203 | 154 |
| 19 | 548 | 220 | 226 | 194 |
因此本文方法达到了减小匿名区域的预期目标,这在实际中有利于保证服务质量,更好地平衡隐私保护与服务质量之间的矛盾关系.
相对匿名度(relative anonymity level)是完成匿名后集合中的对象数与k值的比值.相对匿名度高,代表着匿名区域内有着更多的匿名用户,相应的隐私信息匿名的效果也更好,但这也意味着更高的查询代价.因此,在分析这一标准时,也需要考虑匿名效果与服务效果的平衡,即考虑相对匿名度的稳定性[10].本文实验测试得到的有关相对匿名度的结果如表 3(1 184条数据)和表 4(409条数据)所示.取不同k值进行实验,从实验结果可以看出,其他三种方法的相对匿名度都大于本文的方法,这是由于本文方法优化后,使得匿名面积减小,这也导致区域中包含的对象数减少,从而使得相对匿名度减小,但是满足匿名要求.从另一方面还可以看出,本文方法的相对匿名度在数据量变化、k值变化时都相对较稳定,不会出现较大波动.
| k值 | IC | Casper | Hilbert | Quad-h |
| 5 | 1.99 | 1.35 | 1.44 | 1.21 |
| 7 | 1.94 | 1.27 | 1.40 | 1.13 |
| 9 | 1.90 | 1.23 | 1.37 | 1.12 |
| 11 | 1.82 | 1.20 | 1.32 | 1.05 |
| 13 | 1.61 | 1.18 | 1.31 | 1.06 |
| 15 | 1.66 | 1.18 | 1.27 | 1.04 |
| 17 | 1.66 | 1.26 | 1.29 | 1.07 |
| 19 | 1.67 | 1.26 | 1.25 | 1.07 |
| k值 | IC | Casper | Hilbert | Quad-h |
| 5 | 1.89 | 1.34 | 1.39 | 1.19 |
| 7 | 1.62 | 1.22 | 1.34 | 1.09 |
| 9 | 1.61 | 1.20 | 1.27 | 1.03 |
| 11 | 1.99 | 1.37 | 1.26 | 1.08 |
| 13 | 2.08 | 1.29 | 1.25 | 1.08 |
| 15 | 1.96 | 1.30 | 1.19 | 1.10 |
| 17 | 2.15 | 1.33 | 1.18 | 1.01 |
| 19 | 2.10 | 1.27 | 1.11 | 1.09 |
表 5给出了四种方法在匿名面积和相对匿名度方面的对比.基于空间四分的间隔匿名法匿名区域最大,相对匿名度大,隐秘性强但是位置服务质量受到的影响也大.Casper匿名法和Hilbert匿名法得到的面积有了一定的减小.本文提出的基于空间四分的Hilbert匿名法得到的结果在匿名区域上更小,虽然相对匿名度小,但是比较稳定,相比其他几种方法,在权衡匿名程度和服务质量间的平衡方面有着更良好的结果.
| 方法 | 匿名区域 | 相对匿名度 |
| IC | 匿名面积大,且随着k值增大而大幅增大 | 相对匿名度大,k值不同时相对匿名度变化波动大 |
| Casper | 匿名面积较小,随k值变化也比较平稳 | 相对匿名度较小,数据量少时变化波动明显 |
| Hilbert | 匿名面积较小,随k值变化也比较平稳 | 相对匿名度较小,随着k值变化的波动也比较小 |
| Quad-h | 匿名面积相较其他三种更小,k值增大后的变化也比较稳定 | 相对匿名度小,但是均大于1,k值变化时波动也很小 |
本文将基于空间四分的匿名方法与Hilbert匿名法相结合,在间隔匿名算法的基础上使用Hilbert匿名法进行优化处理,从得出的实验结果看,达到了减小匿名区域的目的,且匿名性较稳定.该方法对于隐私保护与服务质量这一矛盾的平衡有一定的帮助.
| [1] |
韩建民, 林瑜, 于娟, 等. 基于位置k-匿名的LBS隐私保护方法的研究[J]. 小型微型计算机系统, 2014, 35(9): 2088-2093. HAN J M, LIN Y, YU J, et al. LBS privacy preservation method based on location k-anonymity[J]. Journal of Chinese Computer Systems, 2014, 35(9): 2088-2093. DOI:10.3969/j.issn.1000-1220.2014.09.030 |
| [2] |
GRUTESER M, GRUNWALD D. Anonymous usage of location-based services through spatial and temporal cloaking[C]//Proceedings of the 1st International Conference on Mobile Systems, Applications and Services. New York: ACM, 2003: 31-42. DOI: 10.1145/1066116.1189037.
|
| [3] |
MOKBEL M F, CHOW C Y, AREF W G. The new casper: Query processing for location services without compromising privacy[C/OL]. [2017-02-03]. http://www.vldb.org/conf/2006/p763-mokbel.pdf.
|
| [4] |
KALNIS P, GHINITA G, MOURATIDIS K, et al. Preventing location-based identity inference in anonymous spatial queries[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(12): 1719-1733. DOI:10.1109/TKDE.2007.190662 |
| [5] |
邹永贵, 张玉涵. 基于网格划分空间的位置匿名算法[J]. 计算机应用研究, 2012, 29(8): 3059-3061. ZOU Y G, ZHANG Y H. Location-cloaking algorithm based on grid-divided space[J]. Application Research of Computers, 2012, 29(8): 3059-3061. DOI:10.3969/j.issn.1001-3695.2012.08.067 |
| [6] |
王伟芳, 陈明锐, 赵瑶池. 一种改进的基于网格划分空间位置匿名算法[J]. 计算机仿真, 2016, 33(9): 208-210. WANG W F, CHEN M R, ZHAO Y C. An improved location-cloaking algorithm based on grid-divided space[J]. Computer Simulation, 2016, 33(9): 208-210. DOI:10.3969/j.issn.1006-9348.2016.09.044 |
| [7] |
施洪洁. 基于网格和密度的匿名空间查找算法[J]. 课程教育研究:学法教法研究, 2016(11): 249-249. SHI H J. Grid and density based cloaking area search algorithm[J]. Curriculum Education Research: Study Method, Teaching Method Research, 2016(11): 249-249. |
| [8] |
武艳娜. 位置匿名隐私保护技术研究[D]. 杭州: 杭州电子科技大学, 2015. WU Y N. Research on the Location Anonymity Privacy Protection Technology[D]. Hangzhou: Hangzhou Dianzi University, 2015(Ch). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D717533 |
| [9] |
郭娜. 一种基于匿名的位置隐私保护方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012. GUO N. Research on Anonymous Method for Location-based Privacy Preserving [D]. Harbin : Harbin Engineering University, 2012(Ch). http://cdmd.cnki.com.cn/Article/CDMD-10217-1012517019.htm |
| [10] |
金福生, 叶子石, 宋红. 一种基于类四叉树的位置k-匿名算法[J]. 北京理工大学学报, 2014(1): 68-71. JIN F S, YE Z S, SONG H. A similar quadtree based on location k-anonymity algorithm[J]. Transactions of Beijing Institute of Technology, 2014(1): 68-71. |
 2018, Vol. 64
2018, Vol. 64




