文章信息
- 孙长伟, 成谢锋
- SUN Changwei, CHENG Xiefeng
- 混响环境下改进的球谐波域L1-SVD声源定位算法
- Improved L1-SVD Sound Localization Algorithm in the Spherical Harmonic Domain under Reverberant Environments
- 武汉大学学报(理学版), 2018, 64(5): 459-470
- Journal of Wuhan University(Natural Science Edition), 2018, 64(5): 459-470
- http://dx.doi.org/10.14188/j.1671-8836.2018.05.012
-
文章历史
- 收稿日期:2018-03-04

2. 南京邮电大学 电子科学与工程学院,江苏 南京 210003
2. School of Electronic Science and Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210003, Jiangsu, China
声源定位即声波到达方向(direction of arrival, DOA)估计,主要应用于语音增强[1]、声源分离[2]、视频会议[3]、机器人声学[4]等方面,是语音信号处理中非常重要的研究课题.声源定位主要由麦克风阵列实现.常用的阵列主要有线形阵列、圆形阵列、L形阵列等,相比于其他阵列,球面阵列具有三维空间上的对称性,在每个空间方位上都有相同的空间分辨率[5],并且球面阵列可以将采集到的信号变换到球谐波(spherical harmonic, SH)域中进行处理[6],在球谐波域中可以将阵列导向矢量中的DOA信息与频率之间的联系进行解耦[7],为处理宽带声信号带来了方便,避免了经典的宽带聚焦处理和需要对声源位置进行预估的问题[7].另外, 在球谐波域中,导向矢量中不再包含阵列的具体分布信息,这也为阵列信号处理带来了方便[5, 6].因此,基于球面阵列的声信号分析和处理得到了声学研究者的重视,并已广泛应用于声场重建、噪声抑制等诸多领域[8~11].
目前, 常用的球谐波域声源定位算法大都是从阵元域[12]扩展而来,主要包括:SH-MUSIC[13]、SH-ESPERIT[14]、SH-SRP[15]、SH-MVDR[16]、球谐波域最大似然估计算法[17]、PIV算法[18, 19]等.这些算法在进行室内声源定位时,由于受混响影响,定位精度和空间分辨率较低[20].为了解决这一难题,国内外学者提出了许多方法,其中大部分属于时频点筛选类方法.时频点筛选是指通过各种方法将受混响和噪声影响较小的时频点筛选出来用于定位,如Mohan等[21]提出的基于相干检测的时频点筛选方法;He等[22]提出的利用定位结果不确定性的时频点筛选的方法;Faller等[23]提出的模拟优先效应的时频点筛选方法等.但这些方法一般在高混响环境下定位效果不理想.针对高混响环境,Nadiri等[20]根据信号在球谐波域中的特点,提出了一种直接路径占优检测(direct-path dominance test, DPDT)的时频点筛选方法.该方法利用筛选出的来自单一声源的时频点块进行定位,可以大幅减小混响的影响,提高定位性能.Nadiri等[20]将该方法与SH-MUSIC算法[13]相结合,通过数值模拟和实测实验验证了该方法具有较高的抗混响能力.
除了混响问题,常用的球谐波域声源定位算法在噪声鲁棒性方面的表现也并不理想,随着信噪比的降低,定位精度和空间分辨率会急剧下降.而阵元域中基于稀疏表示理论[24]的DOA估计算法具有良好的抗噪能力、较高的定位精度和空间分辨率.目前,稀疏重构声源定位算法基本上都是建立在无混响的条件下[25],在有混响的环境下,由于多径效应的影响使其定位精度下降[26],甚至失效.在室内,混响是不可避免的,因此研究混响条件下的稀疏重构DOA算法具有重要的实际意义.稀疏重构DOA算法主要有协方差矩阵算法[25, 26]、L1-SVD算法[27]、逼近l0范数的算法[28]、基于稀疏贝叶斯学习的算法[29]等.其中,L1-SVD算法[27]通过奇异值分解将多快拍数据模型转换为单测量矢量,大大降低了稀疏重构的运算量;另外,利用噪声的概率分布特性可以解决BP方法[27]中超参数难确定的问题,这两个优点使得L1-SVD算法具有较高的处理效率和定位精度.目前,L1-SVD算法主要应用于窄带信号,对宽带信号如语音信号等的定位精度较差.
为了提高L1-SVD算法的宽带信号处理能力,本文将L1-SVD算法由阵元域[27]扩展到球谐波域,利用球谐波域信号导向矢量中的声源DOA信息与频率解耦的特性,将L1-SVD算法用于宽带语音信号定位,并且与DPDT方法相结合,提高其在混响环境下的定位性能,提出了DPDT-L1SVD宽带声源定位算法.
1 球谐波域阵列信号模型假设由I个全指向性麦克风构成一个球面麦克风阵列,第i个麦克风的三维笛卡尔坐标为:
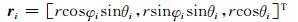
|
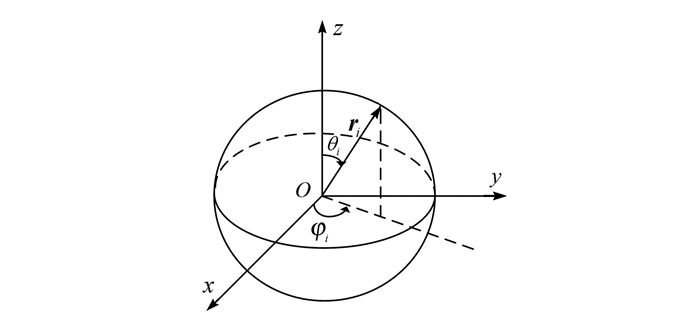
其中,[·]T表示转置,r为球面阵列半径,θi为俯仰角(与z轴正向的夹角),φi为水平角(沿逆时针方向与x轴正向夹角),如图 1所示.L个远场声源发出的声场入射到球面麦克风阵列上,第l个声源的DOA为Ψl=(θl, φl),其波矢量为
|
| 图 1 球坐标系 Figure 1 Spherical coordinate |
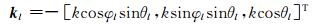
|
对于均匀同性介质波数k=‖kl‖=2πf/c,f为频率,c为声速.球面麦克风阵列采集到的声压在频域中可表示为:
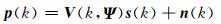
|
(1) |
其中,V(k, Ψ)为每个声源到达球面麦克风阵列的导向矢量构成的矩阵,V(k, Ψ)=[v(k, Ψ1), v(k, Ψ2), …, v(k, ΨL)],v(k, Ψl)为第l个声源的导向矢量,v(k, Ψl)=[v1(k, Ψl), v2(k, Ψl), …, vI(k, Ψl)]T,在远场情况下,vi(k, Ψl)一般为包含声源DOA信息的单位平面波;Ψ为声源的DOA信息矢量,Ψ=[Ψ1, Ψ2,…, ΨL].s(k)为声源信号矢量,s(k)=[s1(k), s2(k), …, sL(k)]T,sl(k)为第l个声源信号的频域表示形式.n(k)为零均值的复噪声矢量,n(k)=[n1(k), n2(k), …, nI(k)]T,ni(k)为第i个麦克风的噪声.本文假设每个麦克风噪声为空间白化噪声,且与声源无关,即满足Rn=E[n(k)nH(k)]=σn2I,其中,Rn为噪声协方差矩阵,σn2表示噪声功率,I为单位矩阵, E[·]表示统计平均,(·)H表示共轭转置.
p(k)为每个麦克风采样到的声压信号构成的矢量,定义如下:
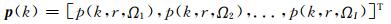
|
其中,p(k, r, Ωi)为第i个麦克风采样的声压信号,第i个麦克风所处的角度方位Ωi= (θi, φi).根据离散球傅里叶变换(discrete spherical Fourier transform, DSFT),将采样到的声压信号变换到球谐波域[11]中:
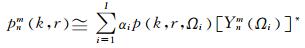
|
(2) |
式中,≅表示近似相等;I为麦克风个数;αi为采样系数,不同采样方案的采样系数是不同的.对于常用的均匀采样αi=4π/I为常数;Ynm(Ωi)为n阶m维的球谐波函数[30],-n≤m≤n;[·]*表示取共轭;上式成立要求n≤N,N为球面麦克风阵列能分解的球谐波系数阶数的上限,与采样方案和麦克风个数I有关.当阵列阶数N和半径r确定后,为了防止出现信号的空间混叠,所处理信号的频率范围要满足kr≤N[25].
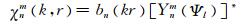
|
(3) |
其中, bn(kr)为模式强度,与声场是远场还是近场以及球面麦克风阵列是开放球还是刚性球有关[11, 30]. bn(kr)是波数k的函数,声场和阵列确定后,波数k由频率决定,因此bn(kr)随频率变化,并且对于不同阶数n,bn(kr)也是不同的.Ψl为声源方位.
将(2)代入(1)式中,将导向矢量矩阵V(k, Ψ)中的元素vi(k, Ψl)用(3)式代替,可得阵列信号的球谐波域模型:
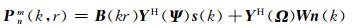
|
(4) |
式中,球谐波系数矢量Pnm(k, r)= [p00(k, r), p1-1(k, r), p10(k, r), p11(k, r), …, pNN(k, r)]T,其维数为(N+1)2×1;B(kr)=diag[b0(kr), b1(kr), b1(kr), b1(kr), …, bN(kr)],其中,diag[·]表示对角矩阵,B(kr)是(N+1)2×(N+1)2的对角矩阵;Y(Ω)=[y(Ω1), y(Ω2), …, y(ΩI)]T,是由阵列每个麦克风位置的球谐波函数构成的I ×(N+1)2的矩阵,Ω=[Ω1, Ω2, …, ΩI]为麦克风位置矢量,y(Ωi)=[Y00(Ωi), Y1-1(Ωi), Y10(Ωi), Y11(Ωi), …, YNN(Ωi)]T;Y(Ψ)的定义与Y(Ω)相似,只是将变量换为声源方位角{Ψl}l=1L,它的维数为L×(N+1)2,是由所有声源DOA信息的球谐波函数构成的矩阵;W=diag(α1, α2, …, αI)为采样系数矩阵,是一个I × I的对角矩阵.
对(4)式等号两边同时乘以B-1(kr),即进行平面波分解(plane-wave decomposition, PWD)[5, 11, 30],可得平面波分解数据模型:
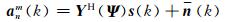
|
(5) |
其中,n(k)=B-1(kr)YH(Ω)Wn(k),由于B-1(kr)是随频率变化的,因此, 若n(k)是高斯白噪声,则n(k)将不再是高斯白噪声;anm(k)是由阵列接收的声场平面波幅度密度的球谐波傅里叶变换构成的矢量,anm(k)=[a00(k), a1-1(k), a10(k), a11(k), …, aNN(k)]T.从式(5)可以看出,经过平面波分解后,球谐波域中的导向矢量变为YH(Ψ), 与频率无关,只包含声源的DOA信息.因此,不用聚焦矩阵就可以对球谐波域中的导向矢量进行频率平滑操作[7],这为处理宽带信号由混响产生的相干信源问题提供了方便,并且导向矢量中不包含阵列的分布信息,不需要根据麦克风位置计算时延,简化了对阵列接收的声源信号的处理过程.
由于语音信号为短时平稳信号,因此,一般对其先进行分帧,再进行短时傅里叶变换(short-time Fourier transform, STFT).将(5)式改写为STFT模型,第τ帧的第ν个频率分量可写为:
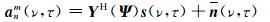
|
(6) |
首先,考虑无混响环境.将L1-SVD算法[27]由阵元域[27]扩展到球谐波域,利用球谐波域信号导向矢量中的声源DOA信息与频率之间的联系进行解耦,将L1-SVD算法用于宽带语音信号定位,提出球谐波域L1-SVD(SH-L1SVD)稀疏重构算法.
在无混响的条件下,将阵列周围的整个空间划分为Q个网格点,形成一系列的角度方位{(θ1, φ1), (θ2, φ2), …, (θQ, φQ)}.每个网格点对应一个导向矢量,根据平面波分解数据模型((6)式),第q个角度方位Ξq=(θq, φq)对应的导向矢量为y(Ξq)= [Y00(Ξq), Y1-1 (Ξq), Y10(Ξq), …, YNN(Ξq)]T.所有方位的导向矢量一起构成一个过完备化的导向矢量矩阵Y(Ξ)=[y(Ξ1), y(Ξ2), …, y(ΞQ)]T,维数为Q×(N+1)2.其中,Ξ=[Ξ1, Ξ2, …, ΞQ].则可将(6)式改写为过完备化的稀疏表示形式:
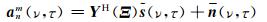
|
(7) |
式中,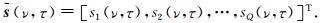
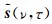
(7) 式虽然对应的是单个时频点的稀疏表示模型,但是由于导向矢量矩阵与频率无关,因此可以方便地将单时频点模型拓展为多时频点宽带稀疏表示模型.将多个时频点的anm(ν, τ)组成接收信号时频点数据矩阵Anm,对应的多个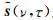
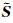
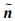
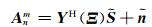
|
(8) |
多时频点的稀疏重构在计算量上比单时频点要大很多,为了减少计算量,利用Malioutov提出的L1-SVD算法思想[27],对Anm进行奇异值分解:
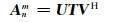
|
(9) |
T为由奇异值构成的对角矩阵,U和V分别为左奇异值矩阵和右奇异值矩阵.根据奇异值分解特性将Anm中的L个信号分量(Anm)SVD提取出来:
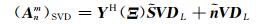
|
(10) |
其中,DL=[IL, 0L×((N+1)2-L)]H,IL为L维单位矩阵,0L×((N+1)2-L)为L×((N+1)2-L)维的全零矩阵.令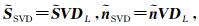
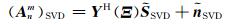
|
(11) |
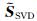
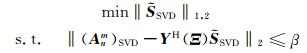
|
(12) |
式中,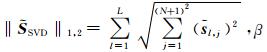
在室内环境下,混响是不可避免的.在混响环境中,麦克风阵列接收的声音信号,一部分是通过直线路径到达的声音信号,简称为直达声信号,包含真实的声源方位信息;另一部分则是经过周围物体反射后到达的声音信号,简称为反射声信号,包含反射的方位信息.若用反射声信号和直达声信号混叠在一起的信号进行稀疏重构,反射声信号会对直达声信号产生干扰,使得重构结果偏离真实声源方位,出现估计偏差;而当反射声信号能量较大时, 可能在稀疏重构时将反射声信号也重构出来,产生虚假声源方位,影响对声源方位的判断.为了提高混响环境下SH-L1SVD稀疏重构算法的定位性能,需要将直达声信号提取出来.
为了从麦克风阵列接收的声音信号中提取出直达声信号,Nadiri等[20]提出了DPDT方法.该方法通过检测接收信号的某一时频点块构成的协方差矩阵Rnm(ν, τ)的有效秩是否等于1,来判断该时频点块包含的信息是否来自于单一声源.对Rnm(ν, τ)进行特征值分解,将特征值按从大到小排序(σ1, σ2, …, σ(N+1)2).若σ1≫σ2,说明该时频点块只包含一个声源信号或只有一个声源信号占优,即:
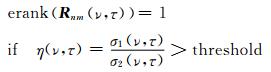
|
(13) |
式中,erank表示有效秩;η(ν, τ)为最大特征值σ1(ν, τ)和次大特征值σ2(ν, τ)的比值,threshold为筛选阈值.
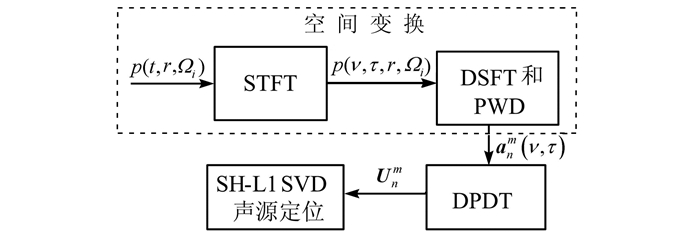
本文将DPDT方法[20]与SH-L1SVD算法相结合,提出DPDT-L1SVD算法,以增强算法对混响的鲁棒性.算法框图如图 2所示,算法主要包含以下3个步骤:
|
| 图 2 DPDT-L1SVD算法框图 Figure 2 Block diagram of the proposed DPDT-L1SVD method |
1) 空间变换:利用短时傅里叶变换(STFT)将阵列i路采样声压信号p(t, r, Ωi)变换到频域,得到p(ν, τ, r, Ωi)(p(k, r, Ωi)的第τ帧的第ν个频率分量),再利用离散球傅里叶变换(DSFT),将I路p(ν, τ, r, Ωi)由频域变换到球谐波域((2)式),最后对球谐波域信号进行平面波分解(PWD)得到频率分量anm(ν, τ).
2) DPDT:由相邻的Jτ个帧和Jv个频率的时频点块通过时间和频率的平均构建协方差矩阵Rnm(ν, τ),对其进行特征值分解,根据(13)式判断该时频点块包含的信号是否来自于一个声源或一个声源信号占优.逐个时频点进行上述操作,将所有通过(13)式检测条件的最大特征值σ1(ν, τ)对应的特征向量unm(ν, τ)取出, 构成矩阵Unm.
3) 声源定位:用Unm替代(8)式中的Anm,对其进行奇异值分解,根据声源个数L,利用(11)式将最大的L个奇异值对应的奇异值向量从左奇异值矩阵中提取出来,并与对应的奇异值相乘作为(Anm)SVD.根据噪声的奇异值选取参数β,与(Anm)SVD一起构建(12)式的凸优化问题,利用MATLAB工具箱CVX进行求解.
关于β的选取问题,文献[18]有相关论述,主要是根据噪声的概率分布来设置,而关于噪声概率分布未知情况下β的选取的相关文献较少.在混响环境下,(Anm)SVD中不仅含有噪声,还含有一些反射声信号,并且由(5)式可知,球谐波域中的噪声不再是高斯白化噪声.目前,关于噪声的具体分布并没有相关文献进行论述,因此β的取值问题在理论上仍无法解决,需要后续工作完善.本文只给出β经验取值,经过反复仿真测试,β取SVD分解得到噪声子空间的最大奇异值的1~2倍.
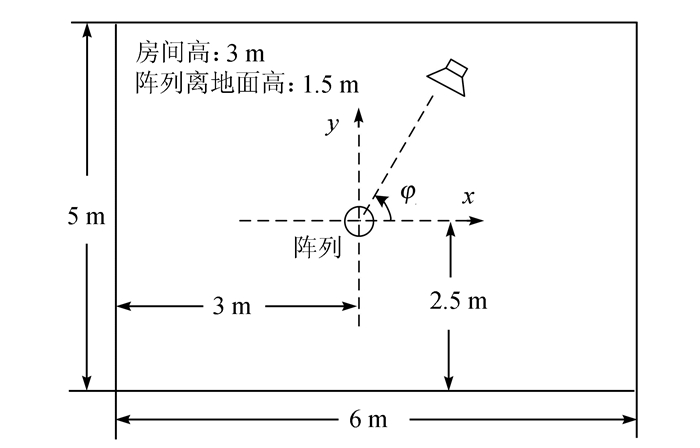
3 仿真实验 3.1 实验条件针对不同混响时间和噪声环境进行仿真实验,测试本文提出的DPDT-L1SVD算法在不同环境下的定位性能,并与SH-L1SVD算法、SS-PIV算法[19]以及DPDT-MUSIC[20]算法进行对比. SS-PIV算法[19]是在伪声强定位算法[18]的基础上增加了子空间分解,将所有时频点的定位结果用直方图表示,利用二维高斯窗函数对直方图进行平滑处理,由平滑后的直方图峰值给出声源方位估计结果.DPDT-MUSIC算法[20]是在SH-MUSIC算法[13]的基础上增加直接路径检测,将通过直接路径检测的时频点块的噪声子空间用于SH-MUSIC算法中,在整个空间进行扫描,计算每个栅格点的空间谱,以最终空间谱的峰值作为声源DOA估计.图 3为仿真实验中球面麦克风阵列在房间中的放置位置示意图.仿真实验中,设定房间的尺寸(长×宽×高)为6 m×5 m×3 m,阵列放置在房间的中心位置,即长、宽、高分别为3、2.5和1.5 m处,阵列中心到每个声源的距离均为1 m,声源水平角为φ(如图 3所示).球面麦克风阵列的参数与MH声学公司生产的em32 Eigenmike球面麦克风阵列的参数一致,即为刚性球,其表面按均匀分布放置32个全指向性麦克风,半径r为4.2 cm.采用像-源法[35]产生刚性球室内声学脉冲响应,与语音信号进行卷积来模拟混响.噪声为高斯白噪声(均值为0,方差为噪声功率).所用的语音信号是从TIMIT语音库[36]中任意选取的,采样频率为16 kHz.仿真中,通过短时傅里叶变换将语音信号变换到频域,变换中采用汉明窗对语音信号进行分帧,每帧长度为256,相邻帧有75%的重叠,参与快速傅里叶变换(fast Fourier transform, FFT)的数据点数为256.时频点块选取的帧数和频率点数分别为Jτ=4、Jν=4.处理的语音信号频率范围为500 ~ 3 850 Hz,这是因为一方面, 频率越低,高阶anm(ν, τ)在低频时受噪声影响越大,故频率不能选太低;另一方面,若信号频率太高,会导致空间混叠.为避免空间混叠,要求kr≤N,即频率f≤Nc/2πr,其中,c为声速,代入阶数N=3和半径r =0.042 m,可计算出频率上限.筛选阈值设置的越高,则筛选出的时频点受混响影响越小,但同时筛选出的时频点个数越少.因此,参照文献[20]仿真实验的设置,将(13)式中的threshold设置为6.
|
| 图 3 仿真实验中球面麦克风阵列在房间中的放置位置示意图 Figure 3 Schematic diagram of the placement of the spherical microphone array in the simulated room |
由于(6)式中得到的第3阶anm(ν, τ)在低频时受噪声影响很大,SH-L1SVD算法在低信噪比情况下有时不能重构出3阶的anm(ν, τ).因此,SH-L1SVD算法采用0~2阶的anm(ν, τ)构成Anm,其他3种算法采用0~3阶的anm(ν, τ)进行计算.SS-PIV算法对所有时频点的定位结果在俯仰角和水平角上以1°为间隔构建二维直方图,平滑高斯窗函数的方差σ=4°,与文献[19]一致.除SS-PIV算法外,其他算法为了减少计算量,采用粗细网格相结合的方式,先对整个空间用粗网格进行划分,在粗网格点进行定位,再在定位结果周围一定区域内用细网格进行精确定位.本文的粗网格以10°为间隔,整个空间上共684个网格点;细网格以1°为间隔,在粗网格定位周围10°的矩形范围内进行网格细分.
若估计的声源方位角度为(θest, φest),其单位矢量为uest=[sinθestcosφest, sinθestsinφest, cosθest]T;真实的声源方位角度为(θreal, φreal),其单位矢量为ureal=[sinθrealcosφreal, sinθrealsinφreal, cosθreal]T;用uest和ureal之间的夹角衡量估计误差ε:
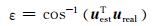
|
(14) |
本文采用均方根误差(root mean squared error, RMSE)来衡量算法的定位精度.若第j次蒙特卡洛实验对第l个声源的估计方位角度为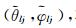
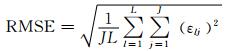
|
(15) |
式中,J为蒙特卡洛实验次数,L为声源个数(单声源时L=1).
3.2 单声源定位性能仿真实验中设置了3种信噪比(signal-to-noise ratio, SNR):0、10和20 dB,6种混响时间:200、300、400、500、600 ms和700 ms,构成共18种不同的环境条件.每种环境条件下,设置24个不同的声源位置,选取两个俯仰角(θ∈{80°, 100°}),即模拟坐和站两个姿势;选取12个水平角(φ∈{0°, 30°, …, 330°}),即以30°为间隔绕球面阵列一周.因此,声源俯仰角和水平角共构成24种组合,即24个不同的声源位置.声源每次放置在一个声源位置进行测试,每个声源位置测试4个从TIMIT语音库中选取的不同的语音信号(2个男声,2个女声),语音信号长度为1 s,并且每个语音进行20次实验.因此,每个环境条件下共进行24×4×20=1 920次蒙特卡洛实验来综合衡量算法的定位精度.
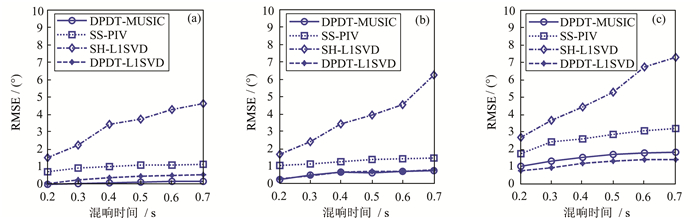
18种环境中,在不同信噪比情况下,4种算法的单声源定位RMSE如图 4所示.由图 4可以看出,这4种方法的RMSE均随混响时间和噪声的增大而增大.如图 4(a)所示,DPDT-MUSIC算法在高信噪比(20 dB)情况下,RMSE最小,DPDT-L1SVD算法次之;当信噪比减小到10 dB时,DPDT-L1SVD算法与DPDT-MUSIC算法的RMSE几乎一致,且小于另外两种算法的RMSE(如图 4(b));而如图 4(c)所示,当信噪比减小到0 dB时,DPDT-L1SVD的RMSE最小,说明在低信噪比情况下,本文算法相较于其他3种算法具有更好的定位精度和噪声鲁棒性.另外,如图 4所示,随混响时间的增大,SH-L1SVD算法的定位RMSE急剧增大.在信噪比为10 dB情况下(如图 4(b)),当混响时间由0.2 s增大到0.7 s时,SH-L1SVD算法的RMSE由1.68°增大到6.23°,说明该算法的定位精度受混响的影响较大;而DPDT-L1SVD算法在信噪比为10 dB,混响时间为0.7 s时的最大RMSE仅为0.8°,说明该算法在高混响环境下也可以得到很高的定位精度,具有较强的抗混响能力.
|
| 图 4 不同信噪比情况下单声源定位均方根误差随混响时间的变化曲线 Figure 4 Effect of the reverberation time on the RMSE of DOA estimation with varying SNR in the single source scenario (a) 20 dB; (b) 10 dB; (c) 0 dB |
将两个声源同时放置在24个位置进行测试.声源1位置的水平角取值φ1∈{0°, 30°, …, 300°, 330°},俯仰角取值θ1∈{80°, 100°},共构成24个位置组合;声源2与声源1的水平角间隔为60°,即水平角取值φ2∈{60°, 90°, …, 0°, 30°},与声源1的俯仰角间隔为20°,即θ2∈{100°, 80°},也构成24个位置组合.两声源距阵列距离仍设置为1 m.语音信号来源与3.2节保持一致,只是从4个语音信号的两两组合中任选4组作为两个声源的语音信号,测试时两个声源同时播放.其他混响时间、信噪比、房间参数、阵列位置等测试参数设置与单声源情况一致.
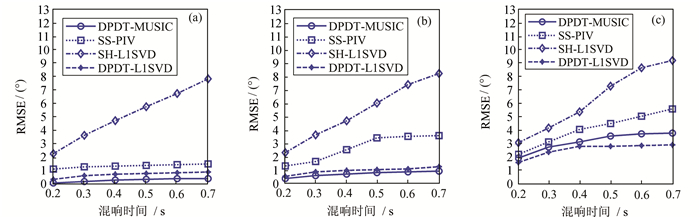
不同信噪比情况下,4种算法的双声源定位RMSE如图 5所示.对比图 4和图 5可以看出,在相同信噪比情况下,4种算法的双声源定位精度均低于单声源情况.由图 5可知,在高信噪比(20 dB)情况下,本文提出的DPDT-L1SVD算法的定位精度仅次于DPDT-MUSIC算法,优于SS-PIV算法,RMSE远远小于SH-L1SVD算法.当信噪比减小到0 dB时,虽然4种算法的RMSE都大幅地增大,但是相比于其他3种算法,DPDT-L1SVD算法的RMSE最小,说明在双声源低信噪比情况下,该算法具有最强的抗噪能力和最高的定位精度.DPDT-L1SVD算法在信噪比为10 dB,混响时间为700 ms时,最大RMSE为1.23°;而SH-L1SVD算法在相同信噪比和混响时间情况下,RMSE为8.23°,说明DPDT-L1SVD算法具有较高的定位精度,且在双声源的情况下仍具有较强的抗混响能力.
|
| 图 5 不同信噪比情况下双声源定位均方根误差随混响时间的变化曲线 Figure 5 Effect of reverberation time on the RMSE of DOA estimation with varying SNR in the two sources scenario (a) 20 dB; (b) 10 dB; (c) 0 dB |
为了进一步验证SS-PIV、DPDT-L1SVD、DPDT-MUSIC和SH-L1SVD算法的空间分辨性能,进行了三声源仿真实验.
仿真设置:声源1、声源2和声源3分别放置于A(θ1=80°, φ1=240°)、B(θ2=100°, φ2=260°)和C(θ3=120°, φ3=180°)三点处;3个语音信号是从3.2节仿真实验中的4个语音信号中任选的,混响时间为700 ms(高混响),信噪比为10 dB.房间尺寸和阵列参数等设置与3.2节一致.由于考察的是空间分辨率,因此每个算法只展示1次仿真实验的结果.
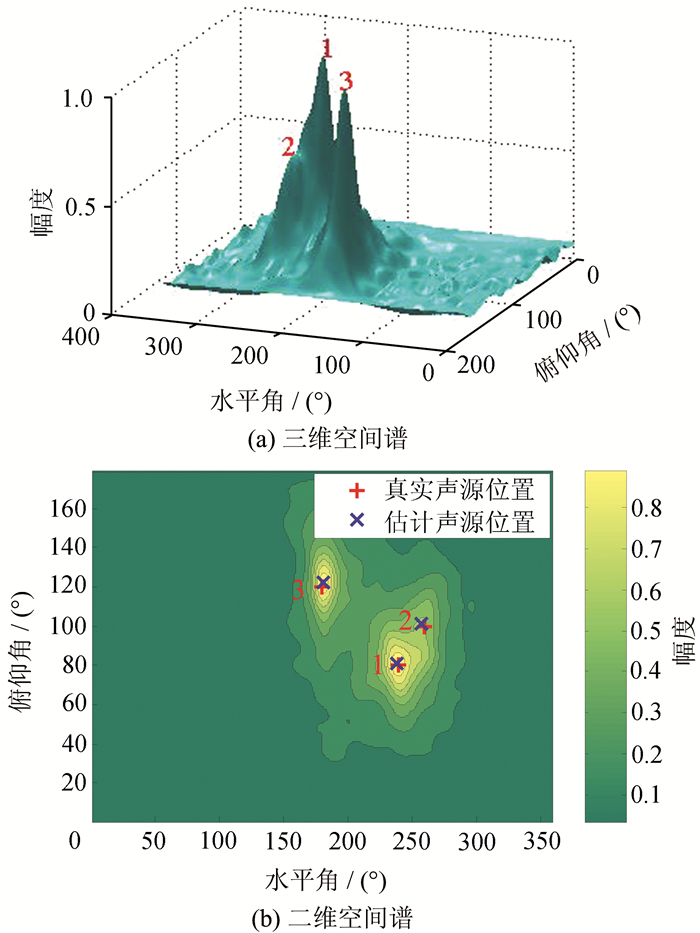
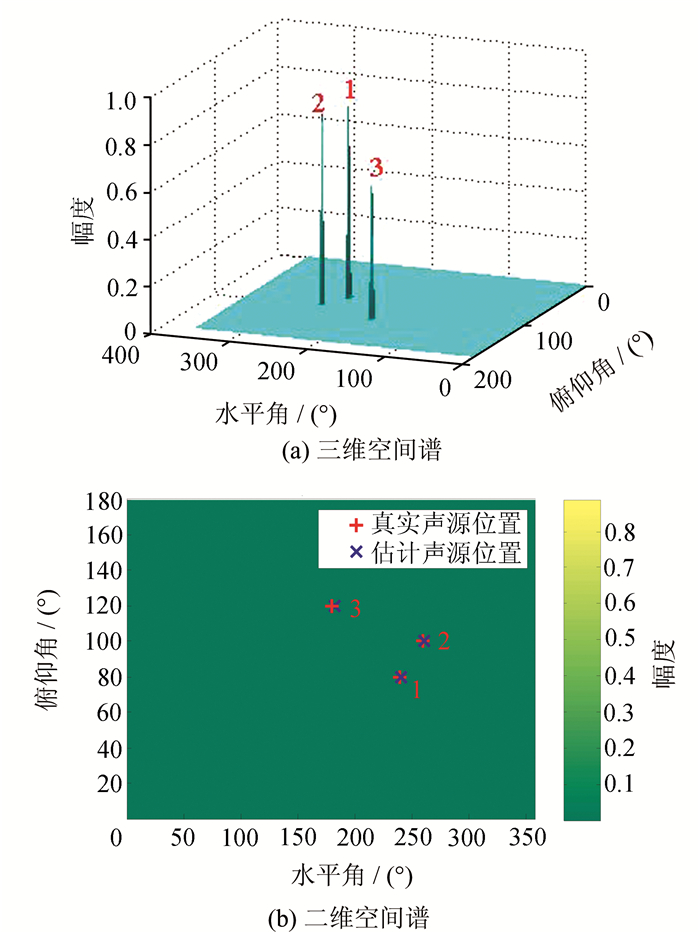
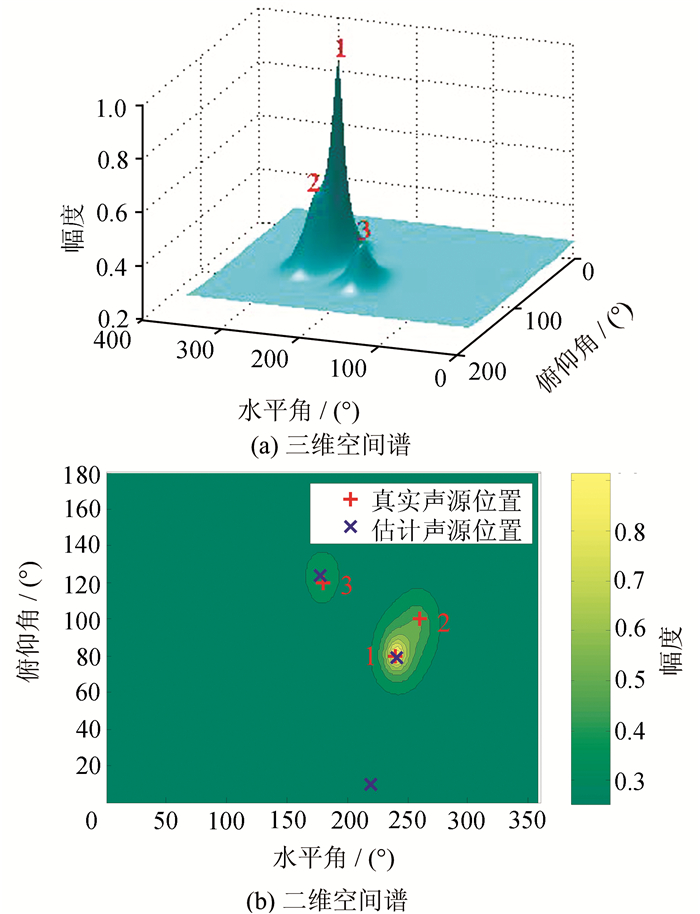
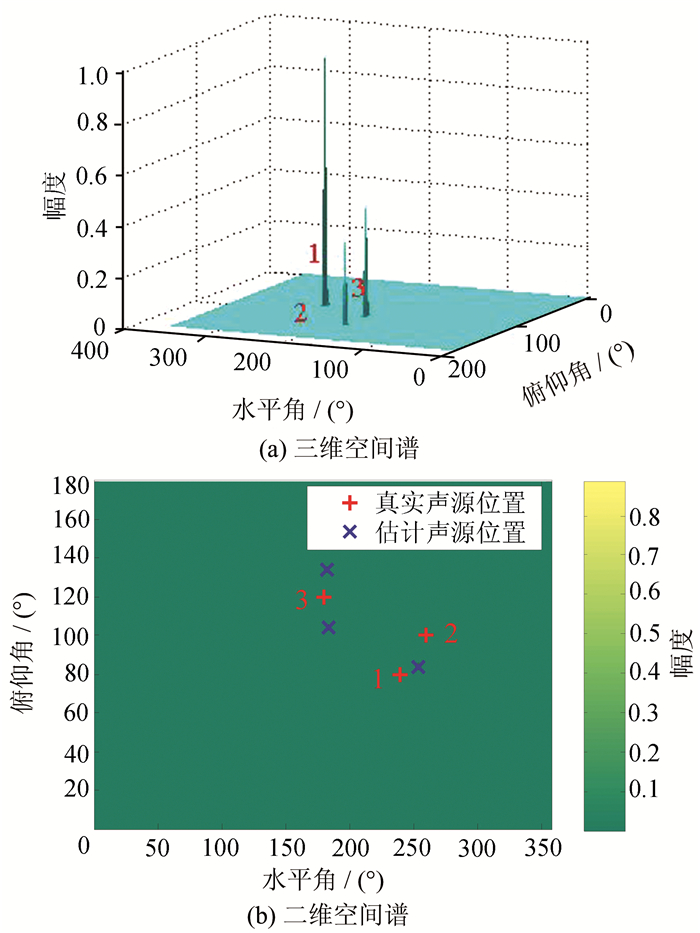
三声源情况下,SS-PIV、DPDT-L1SVD、DPDT-MUSIC和SH-L1SVD算法的定位结果如表 1所示; 估计声源的归一化三维空间谱分别如图 6(a)、7(a)、8(a)和9(a)所示; 估计声源和真实声源的二维空间谱分别如图 6(b)、7(b)、8(b)和9(b)所示,图中用数字标出了每个声源的真实位置.从图 6(b)、7(b)、8(b)和9(b)中可以看出,由于声源3距离另外两个声源间隔比较大,除SH-L1SVD算法外,其他3种算法都能够清楚地从图中识别出其峰所在位置.对于声源1和声源2,由于两者间隔较小,从图 6中可以看出,SS-PIV算法虽然能够清楚地识别出声源1,但是声源2所对应的峰比较小,几乎被声源1的峰所掩盖,仅能勉强识别;对于DPDT-MUSIC算法,从图 8(a)中可以看出声源2的峰已经消失,变成了一个斜坡,完全无法识别声源2的峰的位置,从图 8(b)中可以看出声源2定位在错误的位置.而如图 7和9所示,DPDT-L1SVD算法和SH-L1SVD算法则能够清晰地识别出3个声源,并且空间谱形状比较尖锐.但是从图 9中可以看出,由于声源1和声源2间距较小并且受到混响的影响,SH-L1SVD算法无法准确重构出3个声源信号,空间谱中3个声源峰的位置严重偏离真实声源位置,定位误差比较大.结合表 1可知,SH-L1SVD算法在混响环境下空间分辨率较低,在声源间距较小时无法准确定位声源位置.而本文算法则不受高混响的影响,能够比较准确地定位3个声源的位置.通过对比可以看出,本文算法在多声源高混响条件下,仍具有较高的空间分辨率.
| (°) | |||||
| 声源 | 真实方位 | 估计方位 | |||
| DPDT-L1SVD | DPDT-MUSIC | SS-PIV | SH-L1SVD | ||
| 1 | (80, 240) | (80, 241) | (80, 240) | (81, 238) | (104, 184) |
| 2 | (100, 260) | (100, 261) | (10, 220) | (101, 258) | (84, 254) |
| 3 | (120, 180) | (120, 182) | (124, 178) | (122, 181) | (134, 182) |
|
| 图 6 三声源情况下,SS-PIV算法估计声源的空间谱 Figure 6 Spatial spectra of DOA estimation using SS-PIV algorithm for three sources |
|
| 图 7 三声源情况下,DPDT-L1SVD算法空间谱 Figure 7 Spatial spectra of DOA estimation using DPDT-L1SVD algorithm for three sources |
|
| 图 8 三声源情况下,DPDT-MUSIC算法空间谱 Figure 8 Spatial spectra of DOA estimation using DPDT-MUSIC algorithm for three sources |
|
| 图 9 三声源情况下,SH-L1SVD算法空间谱 Figure 9 Spatial spectra of DOA estimation using SH-L1SVD algorithm for three sources |
为了进一步测试DPDT-L1SVD算法的有效性,通过实测实验对算法的定位性能进行验证.
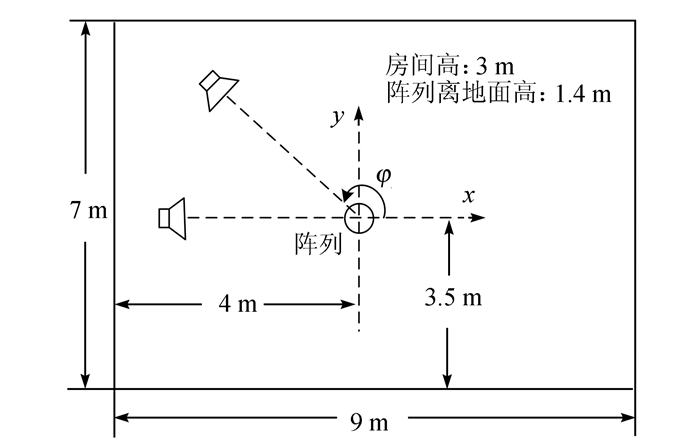
4.1 实验条件实验的房间尺寸(长×宽×高)为9 m×7 m×3 m,房间的混响时间约为300 ms.阵列采用MH声学公司的em32 Eigenmike球面麦克风阵列,属于刚性球,阵列表面按均匀分布放置了32个全指向性麦克风,半径为4.2 cm,阵列阶数为3阶.阵列的采样频率为44.1 kHz,数据采样完成后,将其采样频率降到16 kHz,再进行算法验证,保证与仿真实验采样率一致.阵列放置在房间中长、宽、高分别为4、3.5、1.4 m处,放置示意图如图 10所示.声源与阵列距离为1.5 m.实验中针对两声源情况进行测试,测试了两组声源位置,每组声源位置均进行10次独立测试,每次播放不同的语音信号.从TIMIT语音库中选取10组语音信号,其中有3组中两个声源全为男声,3组中两个声源全为女声,4组中一个声源为男声,另一个声源为女声.每次测试采集4 s信号,从中截取1 s信号进行算法验证.第一组声源为:声源1(θ1=80°, φ1=120°)、声源2(θ2=100°, φ2=180°);第二组声源为:声源1(θ1=80°, φ1=180°)、声源2(θ2=100°, φ2=240°).
|
| 图 10 球面麦克风阵列在实测房间中的放置示意图 Figure 10 Schematic diagram of the placement of the spherical microphone array in the real room |
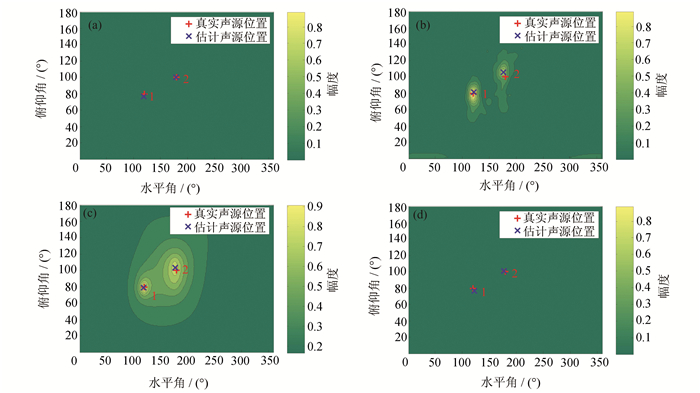
第一组声源处语音信号的归一化二维空间谱如图 11所示.从图 11中可以看出,本文算法和SH-L1SVD算法的空间谱比较尖锐,只有两个点,能够比较清晰地识别出两个声源的位置,而SS-PIV和DPDT-MUSIC算法的空间分辨率较差.根据两组声源位置实测数据,通过4种算法计算得到的各声源位置估计结果的RMSE如表 2所示.从表 2中可以看出,本文提出的DPDT-L1SVD算法在实际房间中可以比较准确地定位出声源位置,由于信噪比比较高,在定位精度上比DPDT-MUSIC算法略低,但高于SS-PIV算法和SH-L1SVD算法.由于房间混响较小,SH-L1SVD算法也能够定位出两个声源的位置.
|
| 图 11 实测实验中双声源情况下估计声源的二维空间谱 (a) DPDT-L1SVD算法;(b) SS-PIV算法;(c) DPDT-MUSIC算法;(d) SH-L1SVD算法 Figure 11 2D view of spatial spectra of DOA estimations for the experimental data in two sources scenario (a) DPDT-L1SVD; (b) SS-PIV; (c) DPDT-MUSIC; (d) SH-L1SVD |
| (°) | |||||
| 声源定位算法 | 第一组声源位置 | 第二组声源位置 | |||
| 声源1 | 声源2 | 声源1 | 声源2 | ||
| DPDT-L1SVD | 2.37 | 2.94 | 2.81 | 2.58 | |
| DPDT-MUSIC | 2.53 | 1.51 | 2.59 | 1.77 | |
| SS-PIV | 2.90 | 2.89 | 3.12 | 2.95 | |
| SH-L1SVD | 2.94 | 3.36 | 3.38 | 5.61 | |
混响噪声环境下的基于稀疏重构理论的声源定位,特别是在球谐波域中进行处理,目前仍然是语音信号处理中需要深入研究的问题.本文将应用于阵元域中的L1-SVD声源定位算法扩展到球谐波域中,提出SH-L1SVD算法,并将其扩展到宽带信号处理中,为提高其在混响环境下对声源的定位能力,将SH-L1SVD算法与DPDT方法相结合,提出了DPDT-L1SVD声源定位算法.由仿真实验结果可知,该算法能够在较高混响和低信噪比的环境下实现较为准确的声源定位.无论是单声源还是双声源情况下,当信噪比较高时,本文算法定位精度仅次于DPDT-MUSIC算法,当信噪比低于10 dB时,本文算法定位精度则是最优的且具有更高的噪声鲁棒性;当混响时间较长时,本文算法的定位均方根误差较小,说明本文算法具有较强的抗混响能力,能够在混响环境下进行较为精确地声源定位.另外,本文算法与DPDT-MUSIC、SS-PIV算法相比,在混响环境下具有更高的空间分辨率.结合仿真实验和实测实验结果,验证了本文算法对单声源及多声源的定位均具有较高的准确性.
| [1] |
HADAD E, GANNOT S, DOCLO S. Binaural linearly constrained minimum variance beamformer for hearing aid applications [C]//International Workshop on Acoustic Signal Enhancement. Frankfurt: Verband Deutscher Elektrotechniker, 2012: 1-4. http://ieeexplore.ieee.org/document/6309415/
|
| [2] |
SAWADA H, MUKAI R, ARAKI S, et al. A robust and precise method for solving the permutation problem of frequency-domain blind source separation[J]. IEEE Transactions on Speech & Audio Processing, 2004, 12(5): 530-538. DOI:10.1109/TSA.2004.832994 |
| [3] |
ZHANG C, FLORENCIO D, BA D E, et al. Maximum likelihood sound source localization and beamforming for directional microphone arrays in distributed meetings[J]. IEEE Transactions on Multimedia, 2008, 10(3): 538-548. DOI:10.1109/TMM.2008.917406 |
| [4] |
李晓飞, 刘宏. 机器人听觉声源定位研究综述[J]. 智能系统学报, 2012, 7(1): 9-20. LI X F, LIU H. A survey of sound source localization for robot audition[J]. CAAI Transactions on Intelligent Systems, 2012, 7(1): 9-20 (Ch). DOI:10.3969/j.issn.1673-4785.201201003(Ch) |
| [5] |
MEYER J, ELKO G. A highly scalable spherical microphone array based on an orthonormal decomposition of the soundfield [C]//IEEE International Con-ference on Acoustics, Speech, and Signal Processing. New York: IEEE Press, 2002: Ⅱ-1781-Ⅱ-1784. DOI: 10.1109/ICASSP.2002.5744968.
|
| [6] |
RAFAELY B. Analysis and design of spherical microphone arrays[J]. IEEE Transactions on Speech & Audio Processing, 2004, 13(1): 135-143. DOI:10.1109/TSA.2004.839244 |
| [7] |
KHAYKIN D, RAFAELY B. Coherent signals direction-of-arrival estimation using a spherical microphone array: Frequency smoothing approach [C]//2009 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics. New York: IEEE Press, 2009: 221-224. DOI: 10.1109/ASPAA.2009.5346492.
|
| [8] |
ABHAYAPALA T D, WARD D B. Theory and design of high order sound field microphones using spherical microphone array [C]//IEEE International Conference on Acoustics, Speech, and Signal Processing. New York: IEEE Press, 2002: Ⅱ-1949-Ⅱ-1952. DOI: 10.1109/ICASSP.2002.5745011.
|
| [9] |
HUANG Y T, BENESTY T. Audio Signal Processing for Next-Generation Multimedia Communication Systems[M]. New York: Springer-Verlag, 2004: 67-89.
|
| [10] |
鄢社锋, 侯朝焕, 马晓川. 从阵元域到模态域阵列信号处理[J]. 声学学报, 2011, 36(5): 461-468. YAN S F, HOU C H, MA X C. From element-space to modal array signal processing[J]. ACT ACUSTICA, 2011, 36(5): 461-468 (Ch). DOI:10.15949/0371-0025.2011.05.001 |
| [11] |
RAFAELY B. Fundamentals of sphe-rical array processing[M]. Heidelberg: Springer-Verlag, 2015.
|
| [12] |
BENESTY J, CHEN J D, HUANG Y T. Microphone Array Signal Processing[M]. Heidelberg: Springer, 2008.
|
| [13] |
LI X, YAN S F, MA X C, et al. Sphe-rical harmonics MUSIC versus conventional MUSIC[J]. Applied Acoustics, 2011, 72(9): 646-652. DOI:10.1016/j.apacoust.2011.02.010 |
| [14] |
TEUTSCH H, KELLERMANN W. EB-ESPRIT: 2D localization of multiple wideband acoustic sources using eigen-beams [C]//2005 IEEE International Con-ference on Acoustics, Speech, and Signal Processing. New York: IEEE Press, 2005: 89-92.
|
| [15] |
RAFAELY B, PELED Y, AGMON M, et al. Sphe-rical microphone array beamforming[M]. Heidelberg: Springer-Verlag, 2010: 281-305.
|
| [16] |
PELED Y, RAFAELY B. Linearly-constrained minimum-variance method for spherical microphone arrays based on plane-wave decomposition of the sound field[J]. IEEE Transactions on Audio Speech & Language Processing, 2013, 21(12): 2532-2540. DOI:10.1109/TASL.2013.2277939 |
| [17] |
HU Y, LU J, QIU X. A maximum likelihood direction of arrival estimation method for open-sphere microphone arrays in the spherical harmonic domain[J]. Journal of the Acoustical Society of America, 2015, 138(2): 791-794. DOI:10.1121/1.4926907 |
| [18] |
JARRETT D P, HABETS E A P, NAYLOR P A. 3D source localization in the spherical harmonic domain using a pseudointensity vector [C]//201018th European Signal Processing Conference. Aalborg: IEEE Press, 2010: 442-446.
|
| [19] |
MOORE A H, EVERS C, NAYLOR P A. Direction of arrival estimation in the spherical harmonic domain using subspace pseudo-intensity vectors[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2017, 25(1): 178-192. DOI:10.1109/TASLP.2016.2613280 |
| [20] |
NADIRI O, RAFELY B. Localization of multiple speakers under high reverberation using a spherical microphone array and the directpath dominance test[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2014, 22(10): 1494-1505. DOI:10.1109/TASLP.2014.2337846 |
| [21] |
MOHAN S, LOCKWOOD M E, KRAMER M L, et al. Localization of multiple acoustic sources with small arrays using a coherence test[J]. Journal of the Acoustical Society of America, 2008, 123(4): 2136-2147. DOI:10.1121/1.2871597 |
| [22] |
HE S J, CHEN H W. Closed-form DOA estimation using first-order differential microphone arrays via joint temporal-spectral-spatial processing[J]. IEEE Sensors Journal, 2017, 17(4): 1046-1060. DOI:10.1109/JSEN.2016.2641449 |
| [23] |
FALLER C, MERIMAA J. Source localization in complex listening situations: Selection of binaural cues based on interaural coherence[J]. Journal of the Acoustical Society of America, 2004, 116(5): 3075-3089. DOI:10.1121/1.1791872 |
| [24] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [25] |
YIN J H, CHEN T Q. Direction-of-arrival estimation using a sparse representation of array covariance vectors[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4489-4493. DOI:10.1109/TSP.2011.2158425 |
| [26] |
HE Z Q, LIU Q H, JIN L N, et al. Low complexity method for DOA estimation using array covariance matrix sparse representation[J]. Electronics Letters, 2013, 49(3): 228-230. DOI:10.1109/TSP.2011.2158425 |
| [27] |
MALIOUTOV D M, MUJDAT C, WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 3010-3022. DOI:10.1109/TSP.2005.850882 |
| [28] |
HYDER M M, MAHATA K. Direction-of-arrival estimation using a mixed l2, 0 norm approximation[J]. IEEE Transactions on Signal Processing, 2010, 58(9): 4646-4655. DOI:10.1109/TSP.2010.2050477 |
| [29] |
LIU Z M, HUANG Z T, ZHOU Y Y. An efficient maximum likelihood method for direction-of-arrival estimation via sparse Bayesian learning[J]. IEEE Transactions on Wireless Communications, 2012, 11(10): 3607-3617. DOI:10.1109/TWC.2012.090312.111912 |
| [30] |
WILLIAMS E G. Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography[M]. New York: Academic Press, 1999.
|
| [31] |
NEEDELL D, VERSHYNIN R. Signal recovery from incomplete and inaccurate measurements via regula-rized orthogonal matching pursuit[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 310-316. DOI:10.1109/JSTSP.2010.2042412 |
| [32] |
NEEDELL D, TROPP J A. CoSaMP: Iterative signal recovery from in complete and inaccurate samples[J]. Applied & Computational Harmonic Analysis, 2009, 26(3): 301-321. DOI:10.1016/j.acha.2008.07.002 |
| [33] |
WANG J, KWON S, SHIM B. Generalized orthogonal matching pursuit[J]. IEEE Transactions on Signal Processing, 2012, 60(12): 1343-1357. DOI:10.1109/TSP.2012.2218810 |
| [34] |
LIPP T, BOYD S. Variations and extension of the convex-concave procedure[J]. Optimization & Engineering, 2016, 17(2): 263-287. DOI:10.1007/s11081-015-9294-x |
| [35] |
JARRETT D P, HABETS E A P, THOMAS M R P, et al. Rigid sphere room impulse response simulation: Algorithm and applications[J]. Journal of the Acoustical Society of America, 2012, 132(3): 1462-1472. DOI:10.1121/1.4740497 |
| [36] |
GAROFOLO J S, LAMEL L F, FISHER W M, et al. DAPRA TIMIT acoustic-phonetic continuous speech corpus [R]. Gaithersburg: NIST Interagency/Internal Report (NISTIR), 1993.
|
 2018, Vol. 64
2018, Vol. 64





