文章信息
- 唐明 , 彭红波 , 胡晓波 , 张焕国 . 2016
- TANG Ming, PENG Hongbo, HU Xiaobo, ZHANG Huanguo . 2016
- 针对RSM轻量防护方法的能量分析
- Power Analysis against Lightweight Countermeasure RSM
- 武汉大学学报(理学版), 2016, 62(3): 235-241
- Journal of Wuhan University(Natural Science Edition), 2016, 62(3): 235-241
- http://dx.doi.org/10.14188/j.1671-8836.2016.03.005
-
文章历史
- 收稿日期:2015-01-24

2. 空天信息安全与可信计算教育部重点实验室,湖北 武汉,430072 ;
3. 北京南瑞智芯微电子科技有限公司,北京,100192
2. Key Laboratory of Aerospace Information Security and Trusted Computing Ministry of Education, Wuhan University, Wuhan 430072, Hubei, China ;
3. Beijing Nari Smartchip Microelectronics Technology Company Limited,Beijing 100192, China
在通讯及数字信号处理高速发展的今天,加密设备的功能和重要性已被许多应用所接受.由于加密算法的硬件形式具有更高的安全性、高效性等,已被多个行业指定为必备的安全防护平台和加密形式.近年来兴起的侧信道分析(side channel analysis,SCA)对加密设备的安全造成了极大的威胁,侧信道分析中的功耗分析方法(power analysis,PA)利用加密中运行的数据与物理功耗泄漏之间的关系进行攻击,已成功攻破多种加密设备.侧信道功耗分析包括:简单功耗分析(simple power analysis,SPA),差分功耗分析(differential power analysis,DPA)[1],相关性功耗分析(correlation power analysis,CPA)[2],互信息分析(mutual information analysis,MIA)[3]等.
由于侧信道攻击威胁的存在,也产生了相应的对抗方法,现有的对抗方法可分为三类:掩码[4]、随机化及功耗互补逻辑.其中掩码对抗方案因实现简单,对抗效果好被广泛应用于工业当中.
掩码主要可以分为一阶掩码、多阶掩码和实用性的轻量化掩码三种.一阶掩码主要出现在1999年到2005年之间,是掩码发展的最初阶段,其掩码方案见文献[5~11];多阶掩码是在一阶掩码的基础上发展而
来的,其算法更加复杂,安全性也更高,但相对应的对硬件资源的要求也更高,代表性的多阶掩码方案见文献[12~15];轻量化掩码则是基于工业化的实际要求而出现的一种掩码方案,它既对算法的安全性有要求,也对硬件资源有要求,常见的轻量化掩码方案文献[16~21]有描述.
本文以Nassar等人[22]提出的轻量级掩码对抗方案RSM作为研究对象,旨在以较小复杂度情况下完成密钥恢复,并分析说明该对抗设计中存在的缺陷,为RSM类轻量级掩码对抗设计提供借鉴.值得说明的是,RSM对抗方法也作为2013年DPA Contest V4(http://www.dpacontest.org/)竞赛的掩码对抗方案,并广泛征集攻击方法.就我们所掌握的资料显示,目前尚无公开的有效攻击方案.
1 RSM掩码方案轻量级掩码方案RSM中有16个字节的基本掩码M={m0,m1,…,m15},该基本掩码值是公开的,每次加密中随机产生一个偏移量offset,记为j,则对于该次加密使用Mj={mj,mj+1(mod16),…,mj+15(mod 16)},对于加入RSM的AES算法,利用M0-15基本掩码会产生MMS0-15,MS0-15,IMMS0-15,IMS0-15四个掩码集合,还有16个掩码S盒,具体计划规则在文献[22]中.
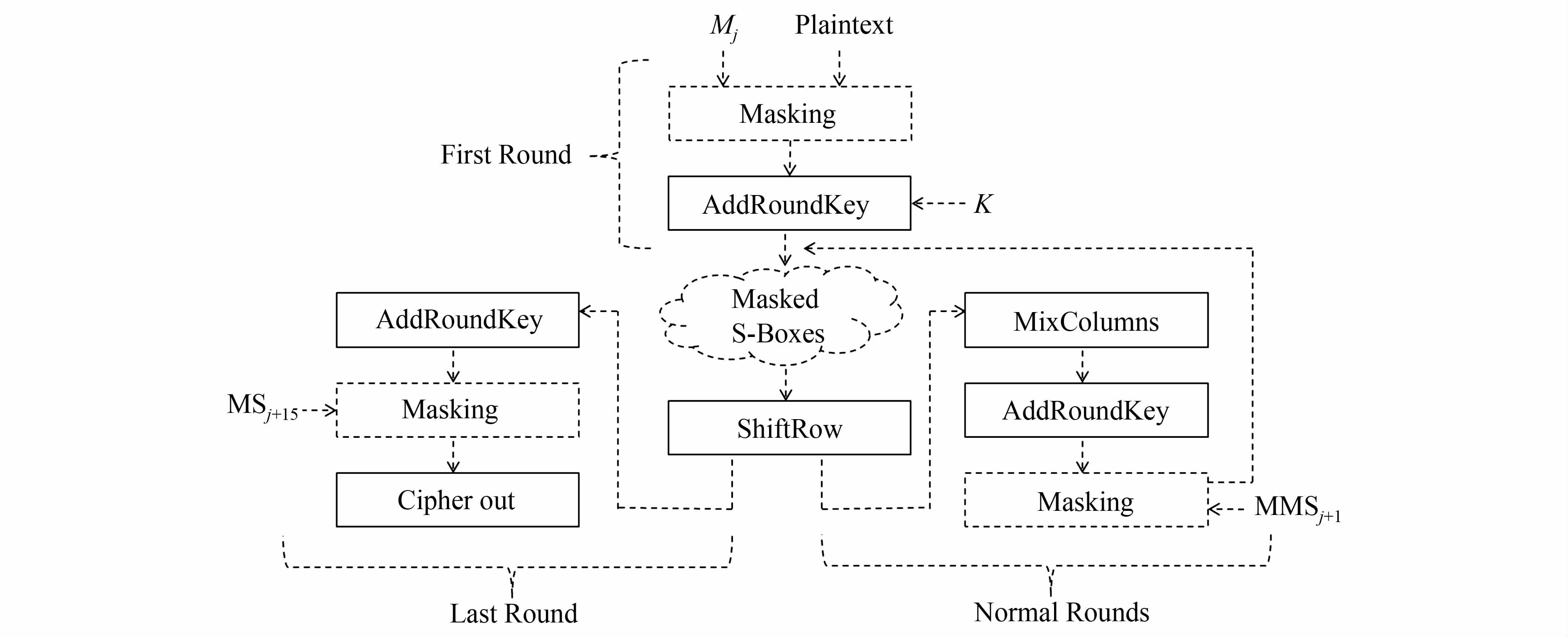
加入RSM方案后的AES算法的加密流程图如图1.
|
| 图 1 加入RSM后的AES加密流程 Figure 1 AES encryption process after joining RSM> |
DPA Contest V4中在ATMega163中对加入RSM对抗方案的AES-256算法进行了实现,算法中所用的基本掩码为M ={0x00,0x0f,0x36,0x39,0x53,0x5c,0x65,0x6a,0x95,0x9a,0xa3,0xac,0xc6,0xc9,0xf0,0xff}.算法的伪代码如下:
| 算法1 AES-256 in DPA Contest V4 |
| 输入:X;//16字节明文,每个字节为Xi,i={0,…,15} |
| RoundKey;//15个16字节的轮密钥 |
| 输出:X;//16字节密文,每个字节为Xi,i={0,…,15} |
| 1:随机产生偏移量offset; |
| 2:X =X ∧Moffset; |
| 3:for r =0:12 do //前13轮 |
| 4:X =X ∧ RoundKey[r];//轮密钥加 |
| 5:for i =0:15 do |
| 6:Xi =MaskedSubBytesoffset+i+r(Xi); |
| //取对应功耗点到集合Ti |
| 7:end |
| 8:X =MixColunms(X); |
| 9:X =ShiftRow(X); |
| 10:X =X^MaskCompensationoffset+1+r; |
| 11:end |
| 12:X =X ∧ RoundKey[13];//最后一轮 |
| 13:for i =0:15 do |
| 14:Xi =MaskedSubBytesoffset+13>+i(Xi); |
| 15:end |
| 16:X =ShiftRow(X); |
| 17:X =X ∧ MaskCompensationoffset+14; |
对算法1的设计方案做简要分析,程序在执行过程中会将加密中所使用的基本掩码先存储起来,每次加密开始时会随机产生偏移量offset后再将掩码按循环左移的顺序读入寄存器进行运算.
当一次加密中的offset确定后,则整个加密过程中的掩码都可以被还原,因此本文主要通过还原offset的值来恢复掩码值,我们可以利用每个掩码字节操作对应功耗的差异来还原掩码,具体方法在第2节中说明.
2 针对RSM对抗的攻击方案 2.1 基于掩码汉明重量的掩码攻击方案本文基于汉明重量模型进行掩码恢复,在汉明重量模型中,攻击者假设功耗和汉明重量成正比,模型可用如下公式表示
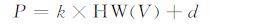
|
(1) |
其中V为正在处理的数据,k和d为由器件特性决定的常数.
根据汉明重量模型,我们可以通过功耗的差异来确定中间结果对应的汉明重量,则对于掩码汉明重量存在差异的RSM掩码方案,也可以用该思想来恢复掩码值.
对于第1节中所描述的轻量级掩码方案RSM,算法必须先确定基本掩码,再通过随机产生offset来确定每次加密所使用的掩码,而将每个掩码字节送至寄存器进行运算时都会产生相应的功耗,这些功耗与掩码字节的汉明重量正相关,如果这些掩码字节的汉明重量存在差异,如DPA Contest V4中所使用的基本掩码的第0个和第15个字节掩码的汉明重量分别为0,8,其他字节汉明重量都为4,我们就可以通过对应功耗的差异来确定每次加密对应的offset的值,再利用一般的功耗分析方法即可完成密钥恢复,下面我们就以DPA Contest V4的RSM掩码方案为例进行掩码恢复.
为了简化说明,对于每一条功耗曲线,第i个掩码字节功耗特征点(这里的功耗特征点是指功耗曲线中与掩码相关的功耗点)集合记为Ei(i=0,…,15),每个掩码字节操作对应的特征功耗点的数量可能不同,我们将集合Ei对应的元素个数记为Ni,对于每个特征点集合的处理可以定义如下:
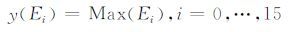
|
(2) |
为了确定offset,定义如下公式:
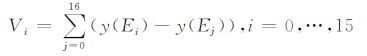
|
(3) |
由于RSM方案中,随机产生offset后再对基本掩码做循环左移操作,同时基本掩码值已知,这样我们就可以通过集合V中元素的差异来确定掩码字节的位置,从而还原offset.
如对于DPA Contest V4所用的RSM基本掩码M中只有m15的汉明重量为8,记Vi(i=0,…,15)中的最大值的下标为t,t对应的就是汉明重量为8的掩码字节的位置,则offset=15-t.
通过以上方法可完成对DPA Contest V4的掩码方案恢复.对于RSM的基本掩码值中有且仅有一个汉明重量最大的掩码字节的情况,掩码恢复算法如算法2.
| 算法2 RSM掩码恢复算法 |
| 输入:Trace;//N条功耗曲线的集合 |
| 输出:offset;//每条曲线对应的offset集合 |
| 1:for i =1:N do//N为功耗曲线数量 |
| 2:Calculating eigenvalues set E for Trace[i]; |
| //加载掩码操作的功耗特征值 |
| 3:for j =0:15 do |
| 4:yj=y(Ej);//根据公式(2)找出特征点集合 |
| 中的最大值 |
| 5:end |
| 6:for k =0:15 do |
| 7:Calculating Vkaccording to equation (3); |
| 8:end |
| 9:if Max(V) =Vx then |
| 10: |
| 11:end |
| 12:offset[i] =15-t; |
| 13:end |
算法2是针对RSM的基本掩码中有且仅有一个汉明重量最大的掩码字节的情况,我们只能对基本掩码的汉明重量存在差异的方案进行掩码恢复.若RSM方案的基本掩码字节的汉明重量都相同,算法2中的思路便会失效.为了弥补这一缺陷,我们希望通过基于中间结果的汉明重量进行掩码恢复,这样就可以通过控制明文使中间值各字节的汉明重量达到算法2的要求,于是我们提出以下改进方案,即基于加密中间值汉明重量的掩码攻击方案.
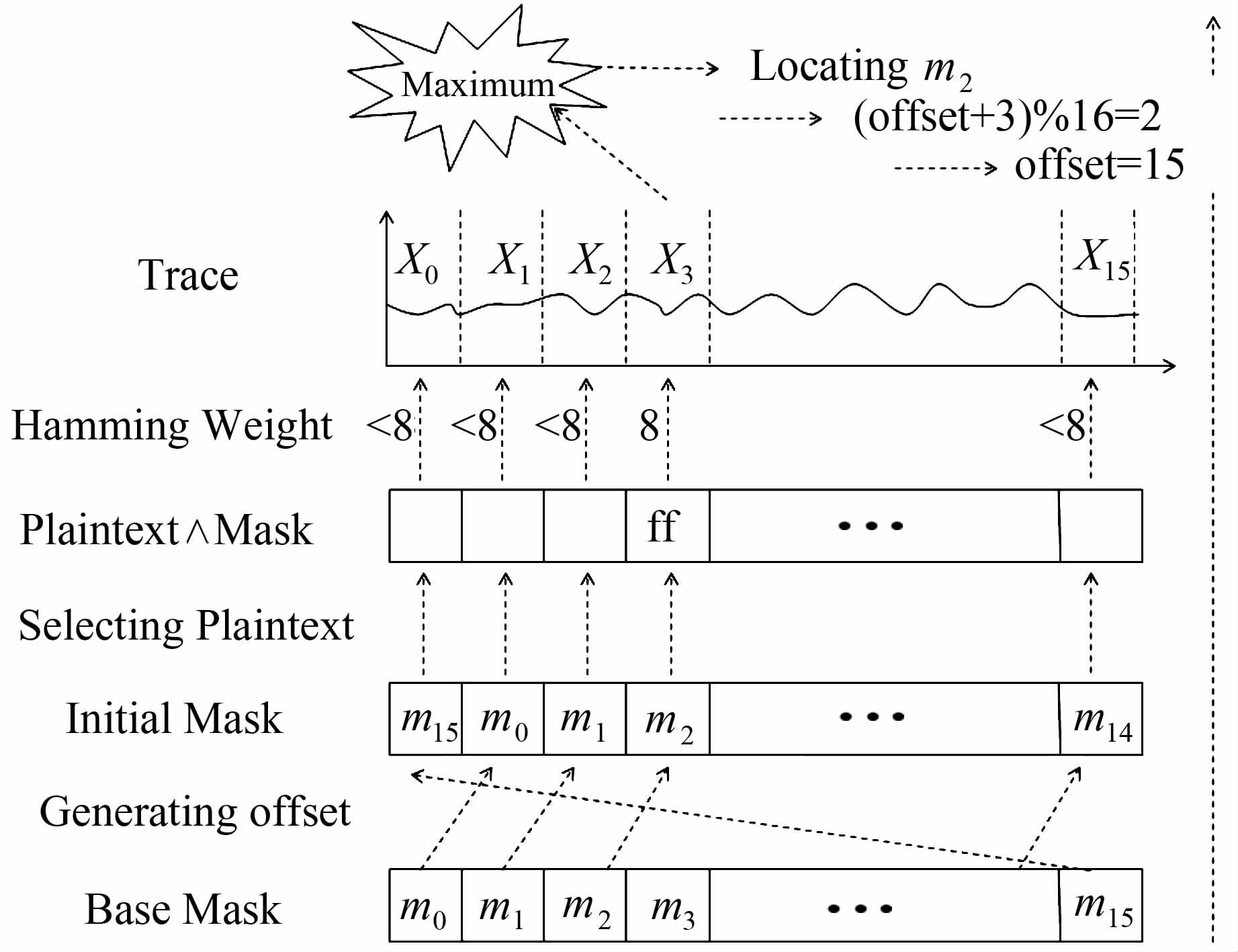
2.2 基于中间值汉明重量的掩码攻击方案对于RSM掩码方案,将中间值的位置定在掩码异或明文操作上,然后通过控制明文使该中间结果的某一字节汉明重量为8,而其他字节汉明重量都小于8,通过该中间结果字节的位置即可确定某一掩码字节的位置,从而确定offset.基本思想如图2所示.
|
| 图 2 基于中间值汉明重量的掩码攻击方案基本思路 Figure 2 Based on the intermediate value with Hamming weight mask attack scheme |
基于以上思路,我们采用以下控制明文方法.
1) 方案1
在基本掩码选择时应保证每个字节取值各不相同,从而避免碰撞攻击.因此有mk,m′k∈Mj,mk≠m′k,选择明文字节pi,使得HW(pi∧mk)=8,又且HW(pi∧mk)≠HW(pi∧m′k),可令明文P={pi,pi,…,pi},则对于异或操作必然会出现汉明重量为8的字节且其他位置的汉明重量都不为8.这种方案的优势和缺点如下:
优势:该方案可使中间结果某一字节的汉明重量为8,其他字节汉明重量都小于8的概率达到100%.
缺点:由于基本掩码已经确定,即mk只有16种取值,因此这种选择明文的方法只能产生16种明文,无法达到攻击所需要的加密次数,即没有足够的功耗曲线.
2) 方案2
为了弥补以上缺点,我们在明文中的任意字节的位置上多引入一个变量px,例如对明文作如下控制.
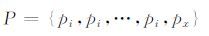
|
其中pi的选择方法与方案1相同,同时在满足HW(pi∧mk)=8的条件,对px的约束条件如下:
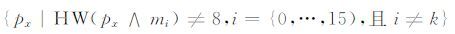
|
通过该改进方法可以解决明文不足的问题,其优势及缺点总结如下:
优势:该方法可使选择明文的数量增加到(256-15)×16×16=61 696,这样可以满足攻击所需要功耗曲线数量.若明文数量仍然不足,则可以继续引入变量字节,这样选择数量可呈指数级增长,进而满足攻击需要.
缺点:该方案产生中间结果的某一字节汉明重量为8且其他字节汉明重量都小于8的概率不能达到100%,而变成了(15/16)×100%=93.75%,因此是一种折中的方法.
通过该改进方案产生可用的明文数量为61 696×93.75%=57 840,仍足够用于恢复密钥,因此可通过该方法进行明文选择.再利用2.1节中相似的方法即可推导得出offset的取值,具体如下:
由本节中的控制明文的方法,有
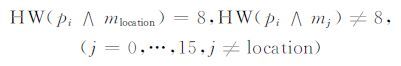
|
通过2.1节中的方法即可确定location的值,当确定location后即可推导出offset的取值,从而恢复掩码.改进算法3如下,如算法.
| 算法3 RSM掩码恢复改进算法 |
| 输入:Trace;//N条功耗曲线的集合 |
| 输出:offset;//每条曲线对应的offset集合 |
| 1:for i =1:Ndo//N为功耗曲线数量 |
| 2:Calculating eigenvalues set E for Trace[i]; |
| //掩码异或明文操作的功耗特征值 |
| 3:for j =0:15 do |
| 4:yj=y(Ej); |
| 5:end |
| 6:for k =0:15 do |
| 7:Calculating Vk according to equation (3); |
| 8:end |
| 9:if Max(V) =Vx then |
| 10:location =x; |
| 11:end |
| 12:Deducing offset[i]; |
| 13:end |
通过算法3的方法即可将每次加密的掩码恢复,然后可以直接利用原始的侧信道攻击方法进行密钥恢复,我们的攻击目标是第一轮轮密钥,现将对于RSM对抗方案的整体攻击流程总结如下:
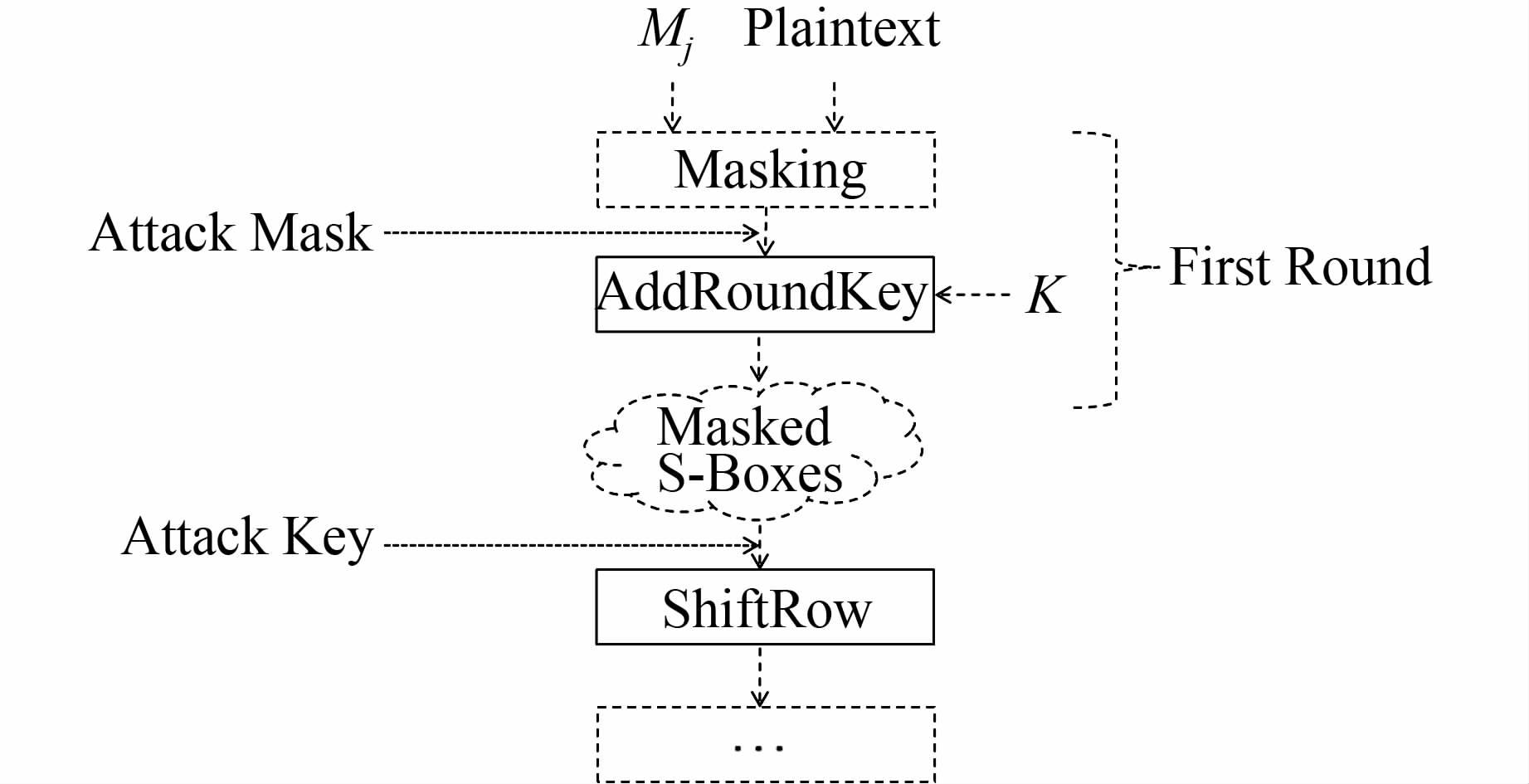
1) 首先对算法的结构进行分析,选择攻击位置,如图3所示.
|
| 图 3 算法结果分析示意图 Figure 3 Schematic diagram of algorithm results analysis |
本文选择第一轮进行攻击,利用第一轮掩码送至寄存器时产生的功耗来恢复掩码,将第一轮S盒的输出位置作为DPA攻击中的选择函数,攻击目标为第一轮轮密钥的16个字节.
2) 如果RSM设计中的基本掩码符合算法2的要求,则随机产生M组明文,否则通过2.2节中的方法选择明文M组.同时采集M条功耗曲线记为Ti,i=1,…,M;Ti[j]表示第i条曲线的第j
3) 通过算法2或者算法3恢复每条功耗曲线对应的掩码值;
4) 建立一个与密钥相关的选择函数,记为D(ki,pi),ki为猜测密钥字节,pi为明文字节,选择S盒输出任意比特作为D函数.根据选择函数为0或1,可以将集合功耗曲线划分成两个子集,分别记为P1和P0,对于一种密钥字节猜测都计算以下公式,得到一条差分功耗曲线.
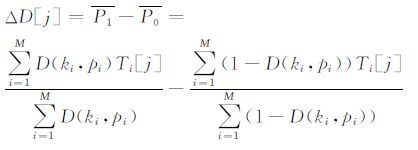
|
(4) |
5) 穷举密钥ki,重复(4),如果密钥字节猜测正确,对应的差分功耗曲线上会出现一个最大峰值,从而恢复该密钥字节.
6) 对于其他密钥字节重复4)和5),最终恢复16字节轮密钥.
3 实验通过DPA Contest V4所提供的数据进行攻击实验,实验采集所使用的实验板为SASEBO-W,其上的ATMega163中烧写入加入RSM对抗方案的AES-256算法,使用的示波器为Lecroy6100A,采样率为500 MHz,为智能卡独立供电的稳压电源Agilent E3631A,及Langer EM进场探头(RF U 5-2)及前置放大器PA303(30 dB~0-3 GHz).官网提供10万条功耗曲线,每条曲线上的点数为435 002,实验中取1 000条曲线进行掩码恢复.
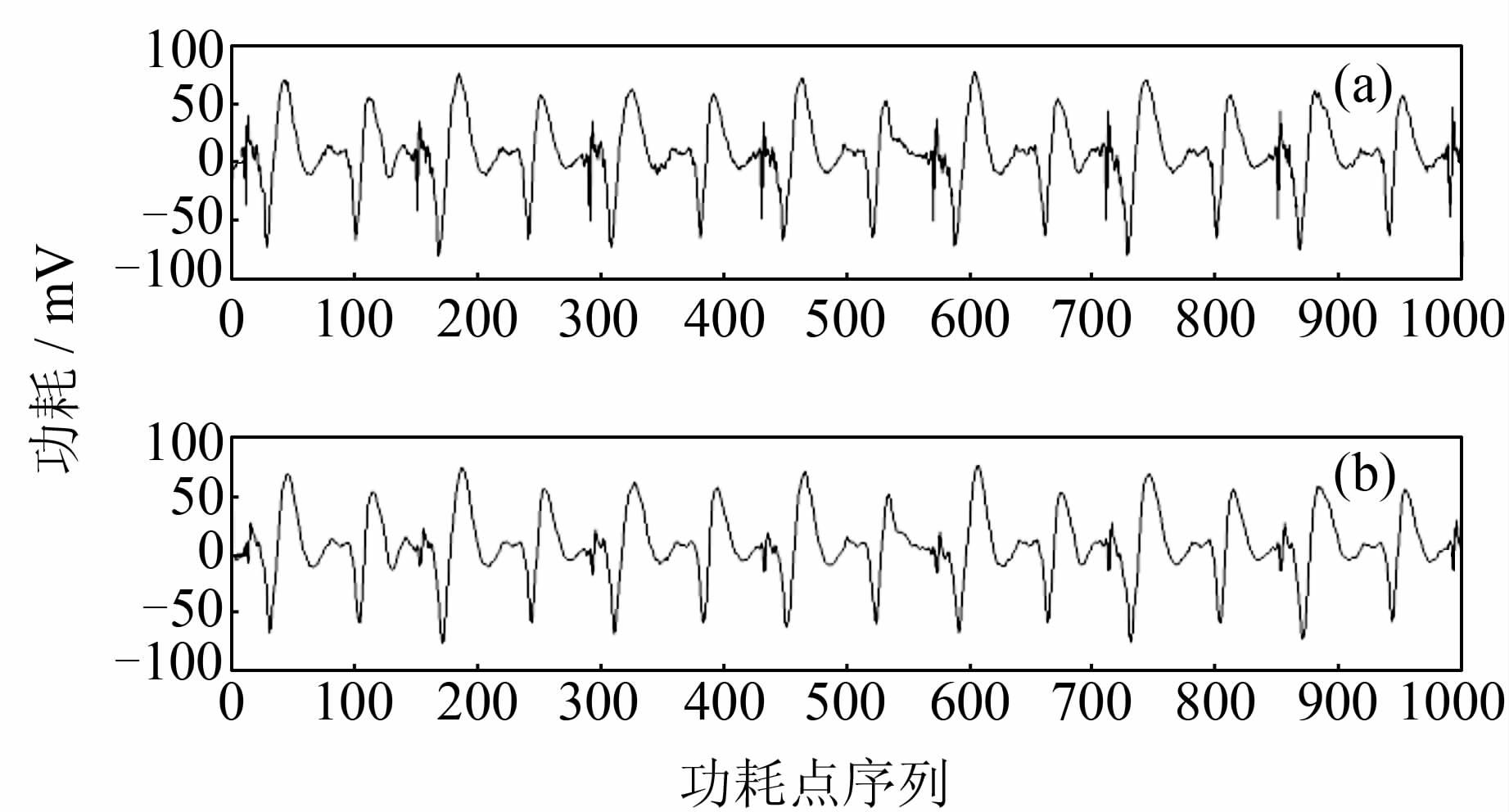
由于本文提出的掩码恢复方案需要利用具体操作对应功耗的差异性,因此可通过降噪来降低噪声干扰从而提高掩码恢复的成功率,同时也可以提高攻击密钥成功率.实验中我们采用Matlab中的低通滤波方法进行降噪.由于ATMega163的工作频率为3.57 MHz,因此我们将低通滤波的截止频率设置为4MHz,降噪前后的曲线如图4所示.
|
| 图 4 低通滤波降噪前(a)后(b)的曲线对比图 Figure 4 Low pass filtering before (a) and after (b) contrast diagram |
图4(a)中为原始的功耗曲线,(b)为滤波后的功耗曲线,其横坐标为功耗点序列,纵坐标为功耗大小.从图4中可以看出,降噪后的曲线变得更加平滑,这样可以提高攻击成功率,下面所做实验都采用滤波降噪后的曲线.
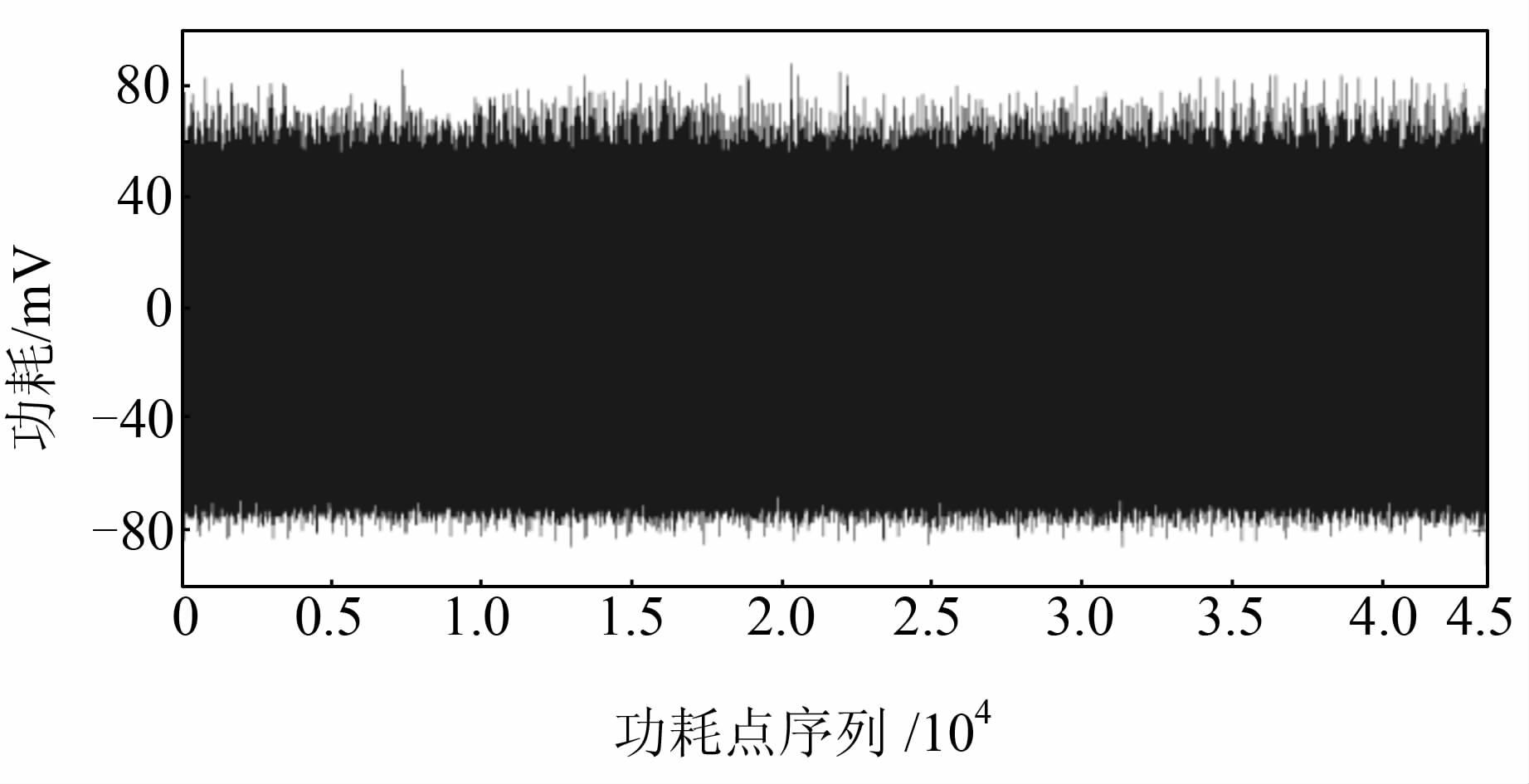
利用基于掩码汉明重量的攻击方法进行掩码恢复实验,先取第1条曲线做验证性实验,所取功耗曲线对应的offset值为8,对应的功耗曲线如图5.
|
| 图 5 Offset为8的功耗曲线示例 Figure 5 The power curve example which offset equal to 8 |
图5为offset为8的功耗曲线,其横坐标为功耗点序列,纵坐标为功耗大小.
对于每一条曲线我利用2.1节中的公式(2)选取特征点集合(具体特征点集合见表1)中的最大值来代表加载掩码字节的功耗.
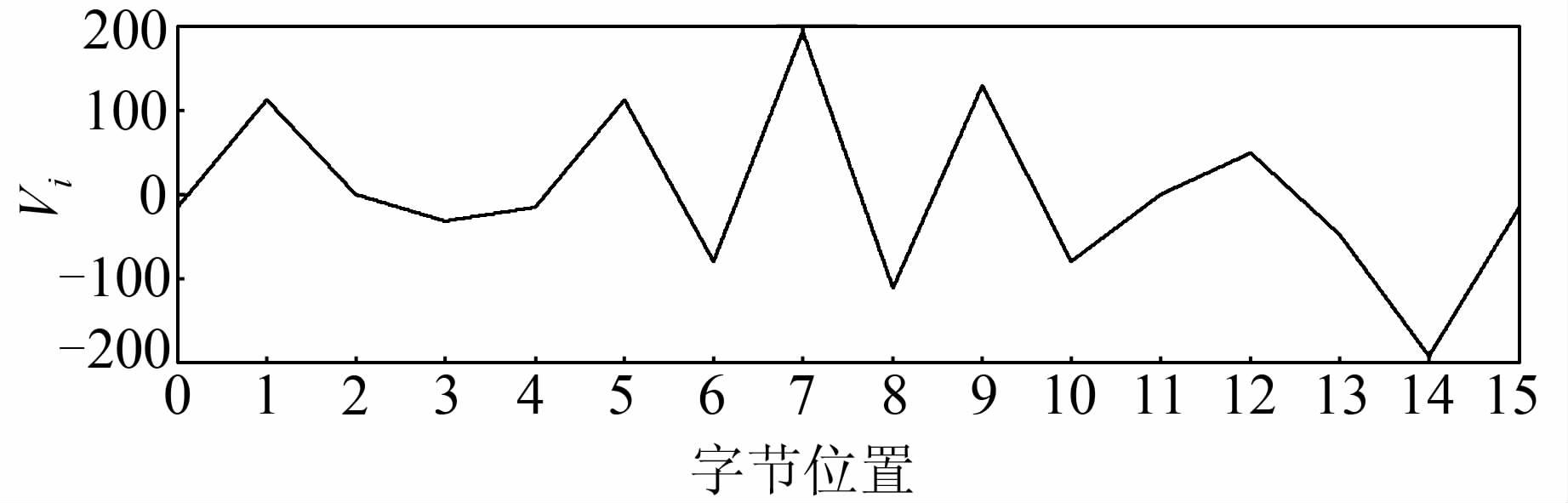
对于DPA Contest V4中所提供的基本掩码,汉明重量为8的掩码字节只有m15,利用2.1节中的公式(3)计算功耗的差异性来确定汉明重量为8的掩码字节的位置,从而恢复当前掩码值,利用公式(3)计算得到集合V,V对应曲线如图6.
|
| 图 6 Offset为8的曲线的掩码定位图 Figure 6 Mask mapping of curves which offset equal to 8 |
图6中横坐标对应公式(3)中Vi(i=0,…,15)中的i,纵坐标表示Vi(i=0,…,15).从图6可以看出,在第7个位置对应的功耗最大,则可以确定第7个位置对应的掩码字节的汉明重量最大,对于DPA Contest V4的掩码方案,该字节即为m15=0xff,依据算法2可以确定该曲线对应的offset=15-7=8,与实际offset值相符.采用相同的方法对1 000条曲线进行掩码恢复,正确率可达到93.1%,实验证明,产生的曲线数量已经足够用于密钥恢复实验.
| 字节 | 特征点位置 |
| 0 | 3956,3957,3958,4236,4246,4247,4248,4378,4801,4802,4803,4804,4805,4806 |
| 1 | 8298,8299,8588,8589,8590,8718,8719,9142,9143,9144,9145,9146,9147,9156,9157,9158,9159 |
| 2 | 12639,12640,12641,12919,12929,12930,12931,13060,13061,13483,13484,13485,13487,13497 |
| 3 | 16980,16981,16982,17261,17271,17272,17402,17825,17826,17827,17828,17829,17830,17839 |
| 4 | 21322,21323,21324,21612,21613,21614,21743,21744,22166,22167,22168,22169,22170,22171 |
| 5 | 25664,25665,25954,25955,26084,26085,26509,26511,26512,26513,26523,26524 |
| 6 | 30005,30006,30007,30284,30285,30295,30296,30297,30849,30850,30853,30863,30864,30865 |
| 7 | 34346,34347,34348,34626,34637,34638,34767,34768,35192,35193,35194,35195,35196 |
| 8 | 38688,38689,38978,38979,38980,39109,39532,39533,39534,39535,39536,39537,39548,39549 |
| 9 | 43029,43030,43031,43309,43310,43319,43320,43321,43322,43450,43451,43875,43876,43877 |
| 10 | 47371,47372,47373,47651,47662,47663,47792,48215,48216,48219,48229,48230,48231,48232 |
| 11 | 51712,51713,51714,51992,52002,52003,52004,52559,52560,52561,52562 |
| 12 | 56054,56055,56344,56345,56346,56475,56899,56901,56902,56903,56913,56914,61515 |
| 13 | 60395,60396,60397,60675,60685,60686,60687,60816,61242,61243,61244,61245,61515,61516 |
| 14 | 64736,64737,64738,65016,65017,65027,65028,65584,65585,66136,66137,66138 |
| 15 | 69078,69079,69080,69358,69368,69369,69499,69925,69926,69927,69928 |
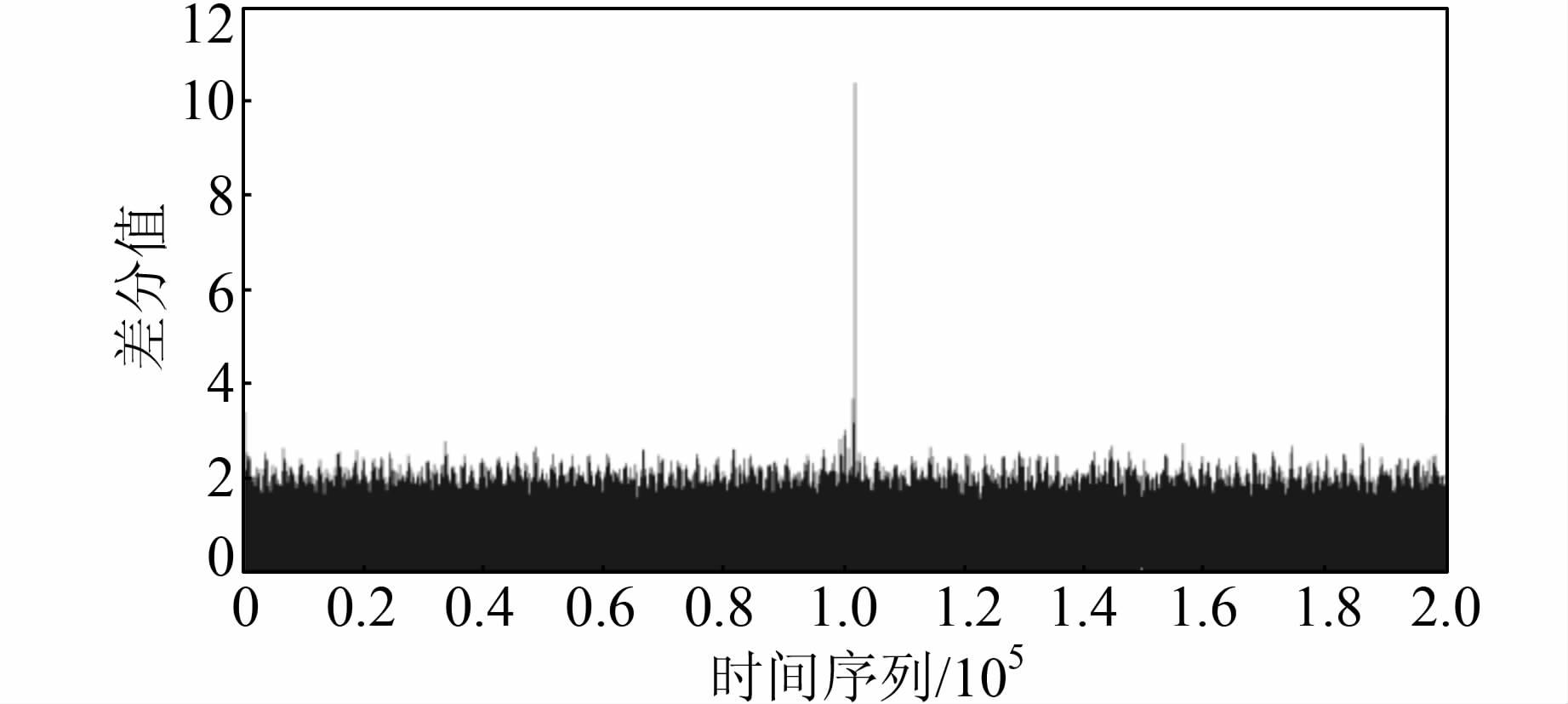
当每一条功耗曲线对应的掩码值被恢复之后,可以利用2.3节的攻击流程进行密钥恢复,在掩码恢复成功率为93.1%的情况下进行攻击,以第0个密钥字节为例,取前200 000万个功耗点进行攻击,当密钥字节猜测正确时,会得到如下差分功耗曲线,如图7.
|
| 图 7 当第0个密钥字节猜测正确时的差分功耗曲线 Figure 7 The differential power curve based on correct of Zeroth key bytes |
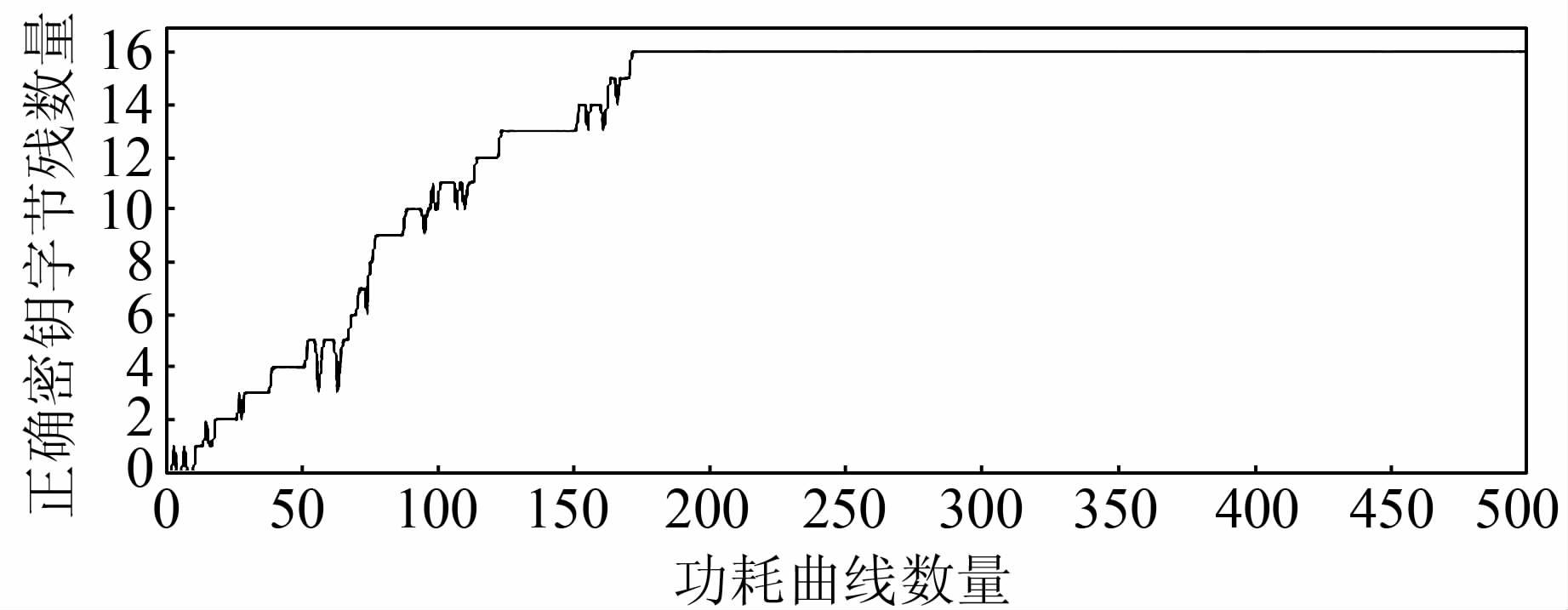
我们对第一轮轮密钥的16个字节进行同样的攻击,实验结果表明,利用原始DPA可以成功完成密钥恢复,功耗曲线数量与所得的正确密钥字节数量的关系如图8所示.
|
| 图 8 攻击所用功耗曲线数量与密钥字节数量的关系图 Figure 8 The relationship of number of power curve and attack correct key bytes |
从图8可知,当功耗曲线数达到200以上时,通过本文的方法可以成功恢复16个密钥字节,DPA Contest V4也对本方法进行了评估[22],评估结果与本实验结果一致.
4 结论加密设备在保护信息安全中起着至关重要的作用,但由于侧信道攻击的存在,给加密设备的安全性造成了极大威胁.在对抗侧信道攻击中,掩码对抗方案以其安全性高的特点被广泛应用于实际中,而在系统小型化、低功耗等需求下催生了轻量级掩码方案.
本文以Nassar等人[22]提出的轻量级掩码对抗方案RSM作为研究对象,对于该对抗方案,现在仍没有公开的有效攻击方案.针对RSM掩码方案,本文提出了一种基于掩码汉明重量的新型攻击方法,利用各掩码字节汉明重量的差异性进行密钥恢复.
进一步考虑到掩码汉明重量无差异的情况,本文将该方法扩展到中间值汉明重量的差异性上,通过选择明文的方法使中间值产生差异,进而通过前述的能量分析方法恢复掩码.通过本文方案可利用单条功耗曲线进行掩码恢复,该方案可成功应用于RSM及扩展后的掩码对抗方案.
我们利用DPA Contest V4所提供数据进行攻击实验,实验结果表明,本文所提出掩码攻击方案可成功恢复每次加密对应的初始掩码值,且攻击成功率可达到93.1%,最终利用差分功耗分析完成了第一轮128比特轮密钥的恢复,验证了本文所提出方法的有效性.本文研究结果可作为掩码对抗,特别是轻量化掩码对抗方法安全性研究的重要借鉴与参考.
| [1] | KOCHER P, JAFFE J, JUN B. Differential power analysis[DB/OL].[2014-07-10].http://link.springer.com/chapter/10.1007 % 2F3-540-48405-1_25 . |
| [2] | BRIER E, CLAVIER C, OLIVER F. Correlation power analysis with a leakage model[DB/OL]. [2014-09-11].http://link.springer.com/chapter/10.1007 % 2F978-3-540-28632-5_2 . |
| [3] | GIERLICHS B, BATINA L,TUYLS P, et al. Mutual information analysis[DB/OL].[2014-09-20].http://link.springer.com/chapter/10.1007 % 2F978-3-540-85053-3_27 . |
| [4] | CHARI S,JUTLA C S, RAO J R, et al .Towards sound approaches to counteract power analysis attacks[DB/OL] .[2014-09-21].http://link.springer.com/chapter/10.1007 % 2F3-540-48405-1_26 . |
| [5] | GOUBIN L , PATARIN J. DES and differential power analysis - The duplication method[DB/OL].[2014-09-21].http://link.springer.com/chapter/10.100 7% 2F3-540-48059-5_15 . |
| [6] | THOMAS S. Messerges. Securing the AES finalists against power analysis attacks[DB/OL].[2014-09-22].http://link.springer.com/chapter/10.1007/3-540-44706-7_11 . |
| [7] | CORON J S, GOUBIN L. On Boolean and arithmetic masking against differential power analysis[DB/OL].[2014-09-22].http://link.springer.com/chapter/10.1007/3-540-44499-8_18 . |
| [8] | GOUBIN L. A sound method for switching between Boolean and arithmetic masking[DB/OL].[2014-09-23].http://link.springer.com/chapter/10.1007/3-540-44709-1_2. |
| [9] | AKKAR M L, GIRAUD C. An implementation of DES and AES, secure against some attacks[DB/OL].[2014-09-23].http://link.springer.com/chapter/10.1007/3-540-44709-1_26 . |
| [10] | GOLIĆ J A, TYMEN C. Multiplicative masking and power analysis of AES[DB/OL]. [2014-09-23].http://link.springer.com/chapter/10.1007/3-540-36400-5_16. |
| [11] | CHARI S, JUTLA C S, RAO J R. Towards sound approaches to counteract power analysis attacks[DB/OL].[2014-09-25].http://link.springer.com/chapter/10.1007/3-540-48405-1_26. |
| [12] | SCHRAMM K, PAAR C. Higher order masking of the AES[DB/OL].[2014-09-26].http://link.springer.com/chapter/10.1007/11605805_14. |
| [13] | CORON J S, PROUFF E, RIVAIN M. Side channel cryptanalysis of a higher order masking scheme[DB/OL].[2014-09-26].http://link.springer.com/chapter/10.1007/978-3-540-74735-2_3. |
| [14] | SUZUKI D, SAEKI M. Security evaluation of DPA countermeasures using dual-rail pre-charge logic style[DB/OL].[2014-09-26].http://link.springer.com/chapter/10.1007/11894063_21. |
| [15] | SAEKI M,SUZUKI D, SHIMIZU K. A design methodology for a DPA-Resistant cryptographic LSI with RSL techniques[DB/OL].[2014-09-27].http://link.springer.com/chapter/10.1007/978-3-642-04138-9_14. |
| [16] | GENELLE L, PROUFF E, QQISQUATER M.Thwarting higher-order side channel analysis with additive and multiplicative maskings[DB/OL].[2014-09-27].http://link.springer.com/chapter/10.1007/978-3-642-23951-9_16. |
| [17] | GOUBIN L, MARTINELLI A. Protecting AES with Shamir’s secret sharing scheme[DB/OL]. [2014-09-27].http://link.springer.com/chapter/10.1007/978-3-642-23951-9_6. |
| [18] | KIM H S, HONG S, LIM J. A fast and provably secure higher-order masking of AES S-box[DB/OL].[2014-08-28].http://link.springer.com/chapter/10.1007/978-3-642-23951-9_7. |
| [19] | DEBRAIZE B. Efficient and provably secure methods for switching from arithmetic to Boolean masking[DB/OL].[2014-09-28].http://link.springer.com/chapter/10.1007/978-3-642-33027-8_7. |
| [20] | RIVAIN M, PROUFF E. Provably secure high order masking of AES[DB/OL].[2014-09-28].http://link.springer.com/chapter/10.1007/978-3-642-15031-9_28. |
| [21] | MESSERGES T. Using second-order power analysis to attack DPA resistant software[DB/OL].[2014-09-28].http://link.springer.com/chapter/10.1007/3-540-44499-8_19. |
| [22] | NASSAR M, SOUISI Y, GUILLEY S, et al . RSM: A small and fast countermeasure for AES, secure against 1st and 2nd-order Zero-Offset SCAs[C]// Deisgn, Awtomation & Test in Europe Conference & Exhibition (DATE’2012). Washington D C: IEEE, 2012:1173-1178. |
 2016, Vol. 62
2016, Vol. 62




