武汉大学学报(理学版) 2017, Vol. 63 Issue (4): 312-316
0

文章信息

廖立敏, 李建凤, 雷光东
LIAO Limin, LI Jianfeng, LEI Guangdong
取代苯胺类化合物相对甜度的构效关系
Structure-Activity Relationship of Relative Sweetness for Substituted Aniline Compounds
武汉大学学报(理学版), 2017, 63(4): 312-316
Journal of Wuhan University(Natural Science Edition), 2017, 63(4): 312-316
http://dx.doi.org/10.14188/j.1671-8836.2017.04.005

文章历史

收稿日期：2016-09-27
Abstract              PDF              Figures              Tables
引用本文
廖立敏, 李建凤, 雷光东. 取代苯胺类化合物相对甜度的构效关系[J]. 武汉大学学报(理学版),2017, 63(4): 312-316.
LIAO Limin, LI Jianfeng, LEI Guangdong. Structure-Activity Relationship of Relative Sweetness for Substituted Aniline Compounds[J]. Journal of Wuhan University(Natural Science Edition) , 2017, 63(4): 312-316.
取代苯胺类化合物相对甜度的构效关系
廖立敏, 李建凤, 雷光东    
内江师范学院 化学化工学院，四川 内江 641100
收稿日期：2016-09-27
基金项目：四川省教育厅科研项目(13ZB0003)，四川省科技厅应用基础项目(2015JY0077) 资助
作者简介：廖立敏，男，副教授，现从事分子结构与性能研究. E-mail: liaolimin523@126.com
通信联系人：雷光东, E-mail:leigdnjtc@126.com
摘要：将有机化合物分子中的非氢原子分为4类，将不同非氢原子自身及非氢原子之间的关系参数化构建出新的结构描述符，对部分取代苯胺类化合物分子结构进行参数化表达，采用逐步回归(SMR)和多元线性回归(MLR)方法构建化合物结构与相对甜度之间的关系模型.该模型的建模相关系数为0.852，“留一法”交互检验的相关系数为0.706，标准偏差为0.293，表明结构描述符能较好地表征化合物分子的结构特征.根据研究结果推测：取代苯胺类化合物苯环上取代基越多，相对甜度值越大，反之相对甜度值越小.
关键词：取代苯胺类化合物     相对甜度     结构描述符     构效关系    
Structure-Activity Relationship of Relative Sweetness for Substituted Aniline Compounds
LIAO Limin, LI Jianfeng, LEI Guangdong    
College of Chemistry and Chemical Engineering, Neijiang Normal University, Neijiang 641100, Sichuan, China
Abstract: The organic molecule non-hydrogen atoms were grouped into four categories, while the different non-hydrogen atoms and the relationship among them were parameterized to build new structural descriptors, and then the molecular structures of some of substituted aniline derivatives were parametric expression. The stepwise regression (SMR) and multiple linear regression (MLR) methods were employed to build the model of the relationship between the structure and relative sweetness (RS/B) of the compounds. The correlation coefficient (R2) of the model was 0.852, the "leave one out" cross validation correlation coefficient (Q2) was 0.706, and the standard deviation (SD) was 0.293. The results showed that the structural descriptors could characterize the molecular structures of the compounds well with good stability and strong predictive power. According to the results, the more substituents the compound has, the greater of its' relative sweetness value will be. Conversely, the relationship is also tenable.
Key words: substituted aniline compounds     relative sweetness     structural descriptor     structure-activity relationship    
0 引言

物质的甜度与其种类、浓度、温度、形态以及掺杂物有关.当苦味物质存在时物质的甜度会减弱.相对甜度(relative sweetness，RS/B)[1]是由物质的甜味值S与苦味值B计算得到，RS/B=lg(S/B)，当S＞B时，则RS/B＞0，物质显示甜味，反之显示苦味.理想的甜味剂可以代替蔗糖产生甜味并降低食品提供的热量，对于人类健康有重要意义.

化合物定量结构-性质关系(quantitative structure-properties relationship, QSPR)研究已广泛用于化合物分配性[2, 3]、溶解性[4]、折光指数[5, 6]、色谱保留行为[7~9]、毒性[10, 11]、酶抑制活性[12]等方面的研究，但在化合物甜味方面的应用[1]较少.本文以部分含取代基的苯胺类化合物为研究样本，将分子中的非氢原子分类后进行参数化染色，构建非氢原子之间的关系，再以非氢原子自身染色值及非氢原子之间的关系作为结构描述符对化合物分子结构进行参数化表达，采用逐步回归(stepwise multiple linear regression, SMR)和多元线性回归(multiple linear regression, MLR)建立化合物结构与相对甜度之间的关系模型，以期为开发寻找新的甜味剂提供参考.

1 材料与方法 1.1 实验材料

本研究选取20种含取代基的苯胺类化合物为研究样本，化合物相对甜度(RS/B)实验值取自文献[1].

1.2 实验方法 1.2.1 化合物分子结构表征

化合物的相对甜度与其分子结构密切相关，构成化合物的原子种类、数目、原子之间的连接方式等都会影响其相对甜度.不同种类非氢原子自身及非氢原子之间的关系对化合物相对甜度有着重要影响，而氢原子仅影响与其直接相连的非氢原子的染色值[13].因此，首先将非氢原子按文献[14]方法分为一、二、三、四类，分别表示与1、2、3、4个其他非氢原子直接相连，如与2个非氢原子直接相连的仲碳原子即为第二类非氢原子，然后在文献[13]基础上，采用(1) 式将非氢原子进行参数化染色.

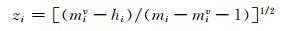
(1)

(1) 式中，i为原子在分子中的编码，mi为非氢原子i核外总电子数，miv为其最外层电子数，hi为与非氢原子i直接连接的氢原子数.

不同种类的非氢原子自身染色值按(2) 式进行分类累加.

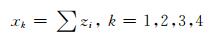
(2)

(2) 式中，k表示非氢原子i的原子类型，zi按(1) 式计算.有机化合物分子中最多含有四类非氢原子，最终可得到4个非氢原子自身染色值对化合物相对甜度贡献项x1，x2，x3和x4.非氢原子之间的关系采用Gaussian形距离关系函数(3) 式计算：

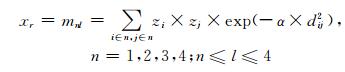
(3)

Zi按(1) 式计算；dij是非氢原子i、j之间的相对距离(即键长之和与碳碳单键键长的比值，如果i、j之间有多条路径，则以最短的为准)；α=0.5;n和l为原子所属类型.化合物分子中四类非氢原子可以组合出以下10种关系项：m11，m12，…，m44，分别简写为x5，x6，…，x14，因此，最多将有14个变量(结构描述符)来描述化合物的结构信息.

(3) 式反映非氢原子之间的相关程度随两者之间的距离增减呈反向变化，随原子自身染色值改变呈正向变化的两方面情况.

1.2.2 建模与评价

采用逐步回归筛选变量后建立多元线性回归模型，以建模相关系数(R2)、“留一法”交互检验相关系数(Q2)对模型质量进行评价.一般认为，R2在0.64~1.0之间，Q2≥0.50，表明模型具有良好的拟合效果、预测能力和稳定性[12].以变量的膨胀因子(VIF)[9]评价变量间是否存在严重共线性，模型变量中最大VIF处于1~10范围内的方程方可接受.

2 结果与讨论

由于研究样本中均无第四类非氢原子，故得到的与第四类非氢原子相关的描述符x4，x8，x11，x13，x14为全“0”项，其余9个描述符用于建模分析.变量较多，且并非所有变量都与化合物的相对甜度密切相关，因此，建模前需要对变量进行筛选.采用逐步回归筛选变量，结果见表 1.

表1 逐步回归结果 Table 1 Results of Stepwise Regression
StepRR2SDFQQ2SDCVFCV最大VIF
10.5410.2930.5887.4500.3490.1220.6552.4991.000
20.6970.4850.5168.0160.5200.2700.6153.1361.004
30.8690.7540.36716.3890.8040.6460.4419.7356.267
40.9240.8530.29321.8440.8400.7060.4158.9887.581
50.9350.8740.28119.4650.8290.6880.4436.16882.698
60.9480.8980.26219.1260.8430.7110.4425.328390.757
70.9550.9120.25317.8680.8610.7410.4364.910748.805
80.9610.9240.24716.6860.5390.2900.7530.563749.266
注：R为相关系数；SD为标准偏差；F为显著性检验值；Q为“留一法”交互检验相关系数；SDCV为“留一法”交互检验标准偏差；FCV为“留一法”交互检验显著性检验值.
表选项

从表 1中可以发现随着变量的引入，R2逐渐增大，同时标准偏差逐渐减小.但是当逐步回归到第5步时，模型变量中最大VIF值达到82.698，远远大于10，变量间共线性严重，方程不可接受.因而，应该选择逐步回归第4步所筛选出来的变量(列于表 2)组合进行建模((4) 式).此时，模型变量中最大VIF为7.581，变量间没有明显的共线性，方程可靠.

表2 苯胺类化合物结构描述符值及相对甜度 Table 2 Structural Descriptor Values and Relative Sweetness of Aniline Compounds
No.化合物x1x9x10x12RS/B[1]Cal.Err.
12-fluoro-5-nitroaniline9.276 82.661 613.494 56.489 41.261.370.11
22-chloro-5-nitroaniline7.512 92.661 613.494 56.489 42.312.470.16
32-bromo-5-nitroaniline7.140 22.661 613.494 56.489 42.712.710.00
42-iodo-5-nitroaniline7.025 42.661 613.494 56.489 42.982.78-0.20
53-nitroaniline6.631 05.834 812.229 23.719 61.211.330.12
62-methyl-5-nitroaniline7.631 02.661 613.494 56.489 42.172.400.23
75-nitro-2-propylaniline7.631 04.411 316.100 86.489 43.022.68-0.34
82-amino-4-nitrophenol8.867 12.661 613.494 56.489 41.961.62-0.34
92-methoxy-5-nitroaniline7.631 03.657 417.600 76.489 42.212.590.38
102-ethoxy-5-nitroaniline7.631 05.968 618.167 76.489 42.872.920.05
115-nitro-2-propoxyaniline7.631 07.723 318.217 96.489 43.463.17-0.29
122-butoxy-5-nitroaniline7.631 09.254 618.219 66.489 42.793.390.60
132-isopropoxy-5-nitroaniline8.631 03.657 420.431 37.183 82.542.53-0.01
145-nitro-2-(vinyloxy)aniline8.045 26.488 018.295 26.489 43.062.74-0.32
153-aminobenzonitrile3.968 17.377 113.608 40.784 50.940.970.03
163-amino-4-chlorobenzonitrile4.850 04.198 214.885 23.548 82.132.11-0.02
173-amino-4-bromobenzonitrile4.477 34.198 214.885 23.548 82.462.35-0.11
183-amino-4-methoxybenzonitrile4.968 15.194 218.991 23.548 81.892.230.34
193-amino-4-ethoxybenzonitrile4.968 17.505 419.558 23.548 82.632.56-0.07
203-amino-4-propoxybenzonitrile4.968 19.260 119.608 43.548 83.112.81-0.30
注：x1为第一类非氢原子参数值；x9为第二类非氢原子之间的关系；x12为第二类非氢原子之间的关系；RS/B为化合物相对甜度；Cal.为化合物相对甜度模型预测值；Err.为误差
表选项
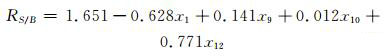
(4)

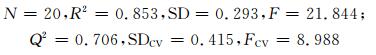
R2=0.853，处于0.64~1.0之间，表明模型具有良好的拟合效果；Q2=0.706，大于0.50，表明模型具有较强预测能力；R2与Q2大小较为接近，说明模型稳定性好.文献[1]依据分子结构的立体参数对该组样本的相对甜度进行了QSPR研究，构建的模型相关系数(R)为0.90(本研究0.924)，标准偏差(SD)为0.32(本研究0.29)，本文结果优于文献[1]结果.

进入模型的变量x1，x9，x10，x12的标准回归系数分别为-1.457，0.470，0.047，1.991.其中x12的标准回归系数最大，对化合物相对甜度影响最为显著，且与相对甜度正相关.x12对应第三类非氢原子之间的关系，而本研究样本中的第三类非氢原子为苯环上被取代基占据的碳原子，说明苯环上取代基越多，化合物可能具有较大的相对甜度值，反之相对甜度值越小.表 2中15号和5号样本与其他样本相比苯环具有较少的取代基，因而显示出较小的相对甜度值，与模型反映的结果一致.x1的标准回归系数也较大，但为负值，说明与化合物相对甜度呈负相关.x1对应于第一类非氢原子自身对化合物相对甜度的影响，说明苯环上取代基数相同时，第一类非氢原子越少，化合物可能具有越大的相对甜度值，反之具有越小的相对甜度值.13号跟14号样本相比，两者苯环上取代基数量相同，但13号样本中的第一类非氢原子更多，因而表现出较小的相对甜度值，与模型反映的结果一致.x9也具有较大的标准回归系数，并且与化合物相对甜度正相关，x9对应于第二类非氢原子之间的相互关系，说明第二类非氢原子数越多，化合物可能具有较大的相对甜度值.7号样本与6号样本相比，取代基位置和数量等均相同，但7号样本(含丙基)比6号样本(含甲基)多2个第二类非氢原子，因而7号样本的相对甜度值比6号样本的相对甜度值大，这与模型反映的结果也是一致的.

综上所述，本研究所建模型能够较好地解释影响化合物相对甜度的分子结构因素.

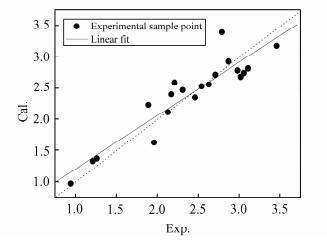
模型对研究样本的相对甜度进行了预测，预测值列于表 2中Cal.列，误差列入Err.列.图 1为预测值与实验值的拟合曲线(实线)，相关系数R=0.924，表明该模型拟合效果良好.另外，发现大部分样本点都落在经过原点的平分线(虚线)附近，说明模型对大部分样本相对甜度的预测是准确的.

图 1 预测值与实验值的拟合曲线 Figure 1 The fitting curve of predicted values vs. experimental values
图选项

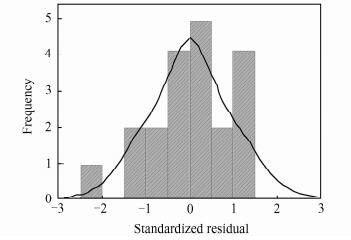
图 2为化合物相对甜度预测值的标准化残差概率分布图，显示标准化残差基本呈正态分布，即大误差样本只是占少数，小误差样本占多数，表明模型质量良好，预测准确性可靠.

图 2 标准化残差概率分布 Figure 2 Distribution of standardized residuals probability
图选项
3 结论

本研究将有机化合物分子中的非氢原子分为四类，将不同非氢原子自身及非氢原子之间的关系参数化构建出新的结构描述符，对部分取代苯胺类化合物分子结构进行参数化表达，采用逐步回归(SMR)和多元线性回归(MLR)方法构建化合物结构与相对甜度之间的关系模型.该模型的建模相关系数为0.852，“留一法”交互检验的相关系数为0.706，标准偏差为0.293，表明结构描述符能较好地表征化合物分子的结构特征.所构建的分子结构描述符无需进行分子构象优化等操作，直观、简单易行.对含取代基苯胺类化合物的相对甜度所建立的QSPR模型，充分考虑了各原子对该类化合物相对甜度的影响.经检验，所得模型具有良好的拟合效果、稳定性和预测能力，模型结果优于文献结果，对于设计、寻找新的有机化合物甜味剂具有一定的参考价值.

参考文献
[1]
IWAMURA H. Structure-taste relationship of perillartine and nitro-and cyanoaniline derivatives[J]. Journal of Medicinal Chemistry, 1980, 23(3): 308-312. DOI:10.1021/jm00177a020
[2]
廖立敏. 卤代苯甲醚结构表征及醇/水分配系数模拟[J]. 计算机与应用化学, 2015, 32(7): 889-892.
LIAO L M. Structural characterization and octanol/water partition coefficient simulation for halogenated anisole compounds[J]. Computers and Applied Chemistry, 2015, 32(7): 889-892. DOI:10.11719/com.app.chem20150728(Ch)
[3]
ANNA R, ANITA S, MONIKA G, et al. Filling environmental data gaps with QSPR for ionic liquids: Modeling n-octanol/water coefficient[J]. Journal of Hazardous Materials, 2016, 303: 137-144. DOI:10.1016/j.jhazmat.2015.10.023
[4]
JIAO L, BING S, WANG X F, et al. Predicting the aqueous solubility of PCDD/Fs by using QSPR method based on the molecular distance-edge vector index[J]. Polycyclic Aromatic Compounds, 2016, 36(4): 527-543. DOI:10.1080/10406638.2015.1028588
[5]
YUAN H, OU H L, CAO C Z. The application of a new approach based on organic homo-rank compounds and homologous compounds to the structure-property relationship study of monosubstituted alkanes[J]. Journal of Physical Organic Chemistry, 2016, 29(1): 42-58. DOI:10.1002/poc.3486
[6]
DUCHOWICZA P R, FIORESSIB S E, BACELOB D E, et al. QSPR studies on refractive indices of structurally heterogeneous polymers[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 140: 86-91. DOI:10.1016/j.chemolab.2014.11.008
[7]
GUPTA S, BASANT N, MOHAN D, et al. Room-temperature and temperature-dependent QSRR modelling for predicting the nitrate radical reaction rate constants of organic chemicals using ensemble learning methods[J]. SAR and QSAR in Environmental Research, 2016, 27(7): 539-558. DOI:10.1080/1062936X.2016.1199592
[8]
SUTTER J M, PETERSON T A, JUTS P C. Prediction of gas chromatographic retention indices of alkylbenzenes[J]. Analytica Chimica Acta, 1997, 342: 113-122. DOI:10.1016/S0003-2670(96)00578-8
[9]
廖立敏, 李建凤, 雷光东. 柠檬皮香气成分结构表征与色谱保留指数预测[J]. 天然产物研究与开发, 2016, 28(1): 90-95.
LIAO L M, LI J F, LEI G D. Structural characterization and chromatographicretention index prediction for aroma components of lemon peels[J]. Nat Prod Res Dev, 2016, 28(1): 90-95.
[10]
堵锡华, 王超. 神经网络法应用于酚类化合物对青海弧菌毒性的预测[J]. 生态毒理学报, 2016, 11(4): 90-94.
DU X H, WANG C. Prediction of the toxicity of phenol derivatives to vibrio-qinghaiensis by neural network method[J]. Asian Journal of Ecotoxicology, 2016, 11(4): 90-94. DOI:10.7524/AJE.1673-5897.20160205003(Ch)
[11]
LIAO L M, HUANG X, LI J F. Structural characterization and acute toxicity simulation for nitroaromatic compounds[J]. Chinese Journal of Structural Chemistry, 2016, 35(3): 449-456. DOI:10.14102/j.cnki.0254-5861.2011-0904
[12]
陈艳, 王思华, 李靖. 昆虫酚氧化酶抑制剂的活性预测模型[J]. 武汉大学学报(理学版), 2017, 62(3): 293-298.
CHEN Y, WANG S H, LI J. Prediction model of the activity of insect phenoloxidase inhibitors[J]. ournal of Wuhan University (Natural Science Edition), 2017, 62(3): 293-298. DOI:10.14188/j.1671-8836.2016.03.014(Ch)
[13]
KIER L B, HALL L H. Molecular Connectivity in Structure-Activity Analysis[M]. England: Research Studies Press, 1986: 82.
[14]
廖立敏, 黄茜, 雷光东. 部分有机污染物灰/水分配系数的定量结构性质关系研究[J]. 南京理工大学学报, 2017, 41(1): 116-122.
LIAO L M, HUANG X, LEI G D. QSPR research on soot/water partition coefficients for some organic pollutants[J]. Journal of Nanjing University of Science and Technology, 2017, 41(1): 116-122. DOI:10.14177/j.cnki.32-1397n.2017.41.01.016(Ch)