文章信息
- 周凌云, 丁立新, 邹桢苹
- ZHOU Lingyun, DING Lixin, ZOU Zhenping
- 多启发式信息蚁群优化算法求解取样送检路径规划问题
- Ant Colony Optimization with Multi-Heuristic Information for Sampling Inspection Path Planning Problem
- 武汉大学学报(理学版), 2017, 63(5): 439-447
- Journal of Wuhan University(Natural Science Edition), 2017, 63(5): 439-447
- http://dx.doi.org/10.14188/j.1671-8836.2017.05.009
-
文章历史
- 收稿日期:2016-10-19

2. 中南民族大学 计算机科学学院, 湖北 武汉 430074;
3. 武汉大学 经济与管理学院, 湖北 武汉 430072
2. College of Computer Science, South-Central University for Nationalities, Wuhan 430074, Hubei, China;
3. Economics and Management School, Wuhan University, Wuhan 430072, Hubei, China
蚁群优化算法(ant colony optimization, ACO)是Dorigo等人最初为解决组合优化问题而提出的一种自然启发式算法[1, 2],具有并行性、分布式、鲁棒性等特点[3].而且,ACO提供了一种通用的算法框架,仅需要相对较少的修改就可以应用于不同的优化问题,使得具体应用的先验信息可以充分的利用,因此广泛应用于旅行商问题(traveling salesman problem,TSP)、车辆调度、社交网络检测、特征提取等多个领域并展现出强大的优势[4, 5].
取样送检是广泛存在于生产活动中的一个重要环节,例如钢铁生产质量检测[6]、海关进出口货物化验鉴定[7]等.取样送检要求从多个节点取得样品送达质检中心.取样送检路径规划问题是指寻找一条从起点经过每个取样节点,最终到达质检中心且全程耗时最短的路径.该问题虽然对工程或者生产没有直接影响,但由于后续生产需要等待质检结果,因此取样时间的延长势必影响后续生产的进程,从而导致影响生产效益.传统的取样送检,往往是依据经验选择路径.随着生产规模逐步增大,取样节点个数不断增加,按经验确定路径的方法显然难以找出适合路径.因此,如何确定取样送检的路径,使得该过程尽可能节省时间,不延误后续生产成为了一个亟待解决的问题.该问题是一种组合优化问题,它类似但不同于旅行商问题[8].不同之处在于取样送检路径的起点与终点是确定的、起点与终点位置不同、整条取样送检的路径不是环路.因此,求解该问题具有重要理论意义与实用价值.
本文首先从分析实际应用出发,给出取样送检路径规划问题的数学模型.然后针对该问题的特点,改进构建解的概率公式,提出一种多启发式信息蚁群优化算法(ant colony optimization with multi-heuristic information,MACO),并对该算法进行了理论分析与实验比较.
1 取样送检路径规划问题描述及数学模型本文的研究是以某钢铁集团有限公司对生产样品进行取样送检为应用背景.公司为满足生产需要,每日早上开班时,需尽快从一扎、二扎、高速线材等多个生产点取样品,送到质检中心检验.每日取样地点不尽相同.通过对取样送检路径规划问题的研究,发现其实质是一个带约束的组合优化问题.取样节点的总数是问题的规模.当取样节点总数较少时容易解决.但随着问题规模的增加,求解时间将呈指数增长.例如,一个16个节点的取样送检路径规划问题,常规需要计算16!,即653 837 184 000种不同条路径的成本,耗费计算时间.
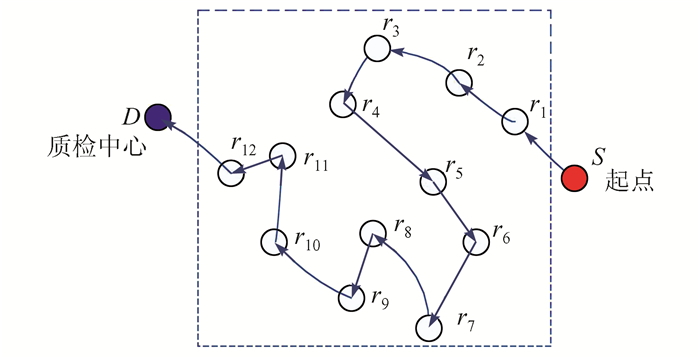
将取样送检路径规划问题描述为:取样车从起点出发,经过每个取样节点,最后送到质检中心.其中,取样节点位于起点与质检中心之间,如图 1所示.要求合理安排取样路线,使得取样开始到取样结束的总路程最短,且取样送检路径满足以下条件:1) 起点与终点的位置固定;2) 每条路径经过的取样节点个数确定;3) 起点与终点不同.
|
| 图 1 取样送检路径例子 Figure 1 An example of sampling inspection path planning problem |
充分考虑上述问题的约束条件和优化目标,本文建立取样送检路径规划的数学模型.设取样节点共n个,路径起点记为S,终点记为D,其他节点记为ri,其中i=1, 2, , …, n.一条完整的取样送检路径可表示为L=Sr1r2…rnD,节点i到节点j之间的距离成本记为dij,起点到第一个取样节点之间的距离记为dSr1,最后一个取样节点到终点的距离记为drnD, 则取样送检路径规划问题数学化之后就是求解
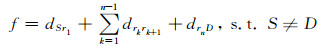
|
(1) |
所示的一个最小值问题.
取样送检路径规划问题与TSP问题具有共同点,都是寻找遍历所有节点的最短路径问题;但是也有其不同之处,那就是具有不同的约束条件.
2 蚁群优化算法(ACO)ACO是Colorni等[1]于1991年首先提出,是模拟自然界真实蚂蚁觅食行为的一种全局优化搜索算法.ACO中的蚂蚁实际上代表的是一个随机构建过程——不断向部分解添加符合定义和约束条件的解成分,从而构建出一个完整的解.每只蚂蚁利用概率决策规则独立地移动,逐步构建路径;蚂蚁之间通过信息素又相互协作.ACO算法的基本框架可描述为[2]:
Step 1 初始化相关参数;
Step 2 判定是否满足终止条件,满足则跳转至Step 3,否则执行Step 2.1、2.2和2.3;
Step 2.1 路径构建;
Step 2.2 局部优化;
Step 2.3 信息素更新;
Step 3 输出最优路径.
该算法中关键的两个部分是路径构建方法与信息素更新策略.ACO算法中最经典的算法最大最小蚂蚁系统(max-min ant system, MMAS)在路径构建过程中采用的概率计算公式为[2]:
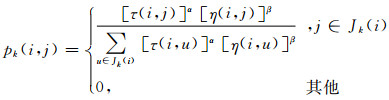
|
(2) |
其中,k是当前可访问节点的个数, u表示可访问的节点,Jk(i)表示蚂蚁当前可访问节点的集合,τ(i, j)表示当前点到可访问节点的信息素,α表示信息素权重,通常取值为1[9].η(i, j)是启发式信息,表示当前点到可访问点的距离的倒数.β表示启发式信息的权重,取值范围为[2, 5][9].
局部优化过程是算法的可选部分,为了改善解的质量往往在算法中加入k-opt算法[10]对蚂蚁构建的解进行局部优化.
MMAS中信息素更新策略是:信息素的取值范围限制在区间[πmin, πmax]内,每条边上的信息素以一定蒸发率减少,只有最优路径上的信息素才增加[3].信息素计算公式为[2]:
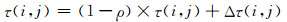
|
(3) |
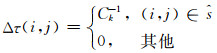
|
(4) |
其中,ρ是信息素的蒸发率,规定0<ρ≤1.Δτ(i, j)是蚂蚁在它经过的边上释放的信息素量,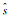
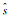
本文为解决取样送检路径规划问题提出多启发式信息蚁群优化算法MACO.该算法中,每只蚂蚁代表从开始节点途经所有取样节点,最终到达质检中心的一条路径.MACO算法采用ACO算法的基本框架,针对取样送检路径规划问题的特点,提出多启发式信息的路径构建规则,同时结合局部优化策略对蚂蚁构建的路径进一步优化.
3.1 路径构建路径构建是算法的关键.经典ACO在求解TSP问题时,是依据信息素矩阵与距离矩阵选择下一个节点从而构建路径.针对取样送检路径规划问题,本文提出一种多启发式信息的路径构建方法.每只蚂蚁表示成为从起点出发,遍历所有节点,最后到达终点的一条路径.设蚂蚁k当前所在的节点为i,则每一个可访问节点j被选择的概率计算公式为:

|
(5) |
(5) 式中η(i, j)是第一项启发式信息,表示当前点到可访问点所需的距离的倒数,距离越长,被选择的概率就越小,它用来引导蚁群优先选择距离花费少的可访问点.μ(s, j)是第二项启发式信息,表示起点到将选择点距离的倒数,用来引导蚂蚁优先选择距起点近的可访问点.第二项启发式信息是针对取样送检路径规划问题的特点而对经典ACO算法进行的主要改进.该项启发式信息能够使得蚂蚁移动的总体方向是指向终点的.(5) 式中,α、β和γ这3个参数的大小分别表示信息素、第一项启发式信息和第二项启发式信息在蚂蚁构建路径时的相对重要性,即权重.依据(5) 式计算所有可访问节点的概率,然后采用轮盘赌法选出下一个访问节点加入到蚂蚁的路径中,概率越大的节点被选的可能性就越高.
3.2 信息素更新蚂蚁更新信息素步骤的正向反馈作用是促使算法能够找到最优路径的主要机制.MACO算法中,信息素更新采用MMAS算法的更新方法.蚂蚁构建的路径越短,在该路径的边上释放的信息素就越多.这个机制随着迭代过程反复执行,迭代最优路径上的边在以后的路径构建过程中将会以更高的概率被选择.
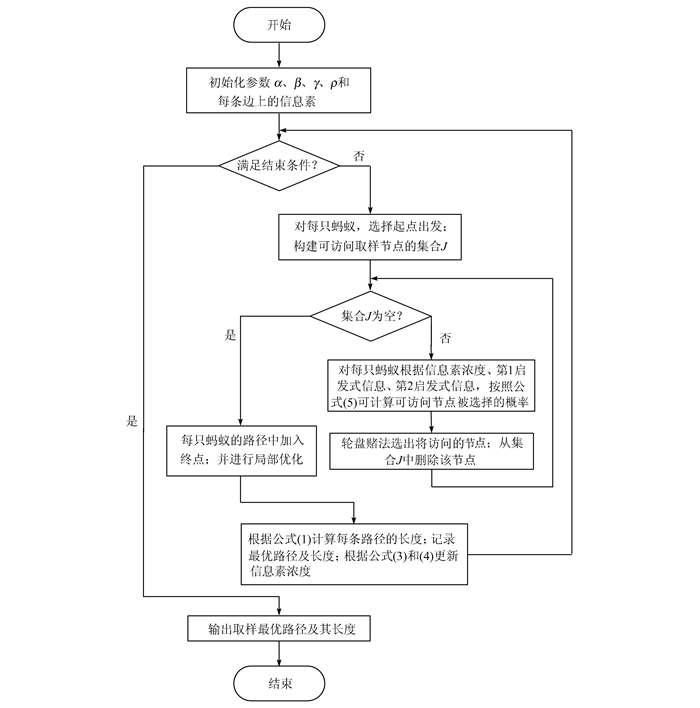
3.3 MACO算法步骤MACO算法流程图如图 2所示.从图 2可看出,MACO算法使用了ACO算法的基本框架,通过迭代在搜索空间中寻找最优路径.迭代过程包括了一个由信息素和两项启发式信息给出的偏向性的路径构建过程.相对于ACO算法,MACO算法的主要改进在于路径构建过程中选择下一个访问节点的概率计算公式中增加了一项启发式信息.这项改进主要是针对取样路径优化问题而设计.在MACO算法中,优先选择距离当前点近, 同时距离起点也近的节点作为下一个访问点.因此,新增的启发式信息μ(s, j)使得蚂蚁在选择下一个访问节点时以较大的概率选择距离起点近的节点.取样送检路径规划问题中,整条路径的起点与终点是固定的,有了这项新增的启发式信息,蚂蚁就能够尽量沿着从起点指向终点的方向移动,从而使得整条路径的长度最短.MACO算法增加了一个参数γ,表示新增启发式信息的相对重要性.这个参数可以参考α和β的取值范围来设置.
|
| 图 2 MACO算法流程图 Figure 2 The flow chart of MACO |
由于MACO算法的这项改进并不会增加整个时间复杂度,所以MACO算法的时间复杂度与ACO算法是相等的.
3.4 MACO算法收敛性分析Stützle和Dorigo在文献[11]中给出了保证蚁群算法收敛的一般性条件并证明了简化的蚁群算法能以概率1收敛.刘彦鹏[12]在此基础上进一步证明了当蚂蚁个数与迭代次数的乘积非常大时,算法将以概率1收敛到全局最优解.苏兆品[13]从鞅理论角度论证了蚁群算法能在有限步内收敛到全局最优解集.本节在这些收敛性分析的成果上,对MACO算法的收敛性进行分析.
引理1 设P*(t)表示算法在t次迭代中至少有一次找到最优解的概率,则对于任意小的ε>0, 都存在一个足够大的t,满足

|
且

|
证明见文献[11].
根据引理1可知ACO算法以概率1收敛,MACO是在ACO算法的基础上增加了多个启发式信息,并结合了局部搜索策略.其中,局部搜索策略只是局部调整蚁群构建的路径,并不影响ACO算法的收敛性[11].MACO算法根据取样送检路径问题的特性提出了在ACO概率计算公式上增加了启发式信息,仍然能以概率1收敛.依据ACO算法的收敛性可以得到MACO的收敛性定理.
定理1 ACO算法的收敛概率趋于1,则MACO算法的收敛概率也趋于1.
证 设MACO算法收敛概率为P'*(t),p'ij*(t)为MACO算法t时刻蚂蚁在节点i时选择下一个节点j的概率,pij*(t)为ACO算法t时刻蚂蚁在节点i时选择下一个节点j的概率,根据(5) 式,有
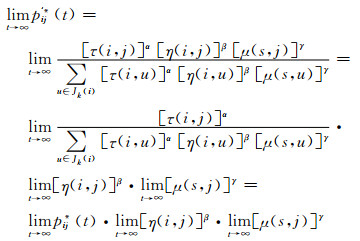
|
因为,启发式信息η(i, j)和μ(s, j)表示的是节点i到节点j的距离的倒数与起点S到节点j距离的倒数,它们都是常值,不随迭代次数t而变化.于是,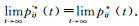

实际环境中送检节点通常在60个以内.为了验证MACO算法求解取样路径优化问题的有效性并测试算法性能,本节采用9个问题算例(节点规模从10到70,其中node10、node20、node30、node45和node60是个数分别为10、20、30、45和60的100×100内随机产生的节点,bays29、eil51、berlin52和st70则是标准库TSPLIB[14]中的例子)进行仿真实验.实验运行在一台配置为:Intel Core(TM)2 Duo CPU E4600 @ 2.40GHz;内存2GB;操作系统为Windows 8专业版的计算机上.所有的算法在Matlab 2012下进行仿真.
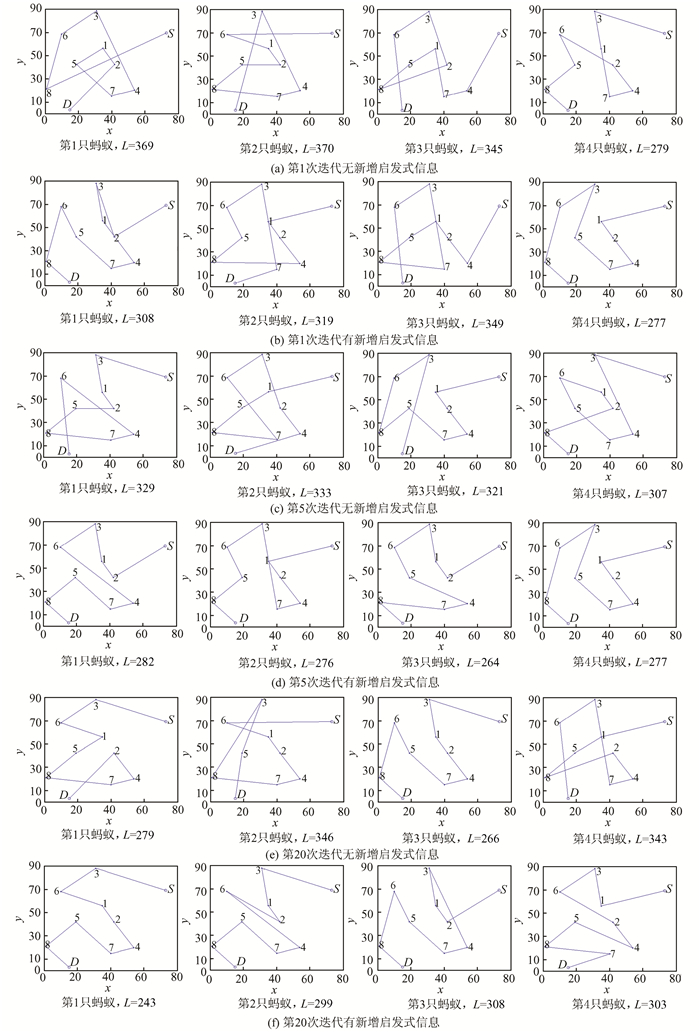
4.2 新增启发式信息对路径构建的影响为了检验新增启发式信息对蚂蚁构建路径的影响,以一个具有10个节点的取样送检路径规划问题为例,采用4只蚂蚁的种群,分别不使用新增启发式信息和使用新增启发式信息,观察第1次、第5次和第20次迭代时蚂蚁构建的路径长度对比,见图 3.
|
| 图 3 新增启发式信息对蚂蚁构建路径的影响 Figure 3 The influence of the new heuristic information on the paths of ants |
第1次迭代时每条边上的初始化信息素都相等,根据(2) 式和(5) 式可知,蚂蚁移动时选择节点主要受启发式信息的影响,而不受信息素的影响,此时最能体现出第二项启发式信息对蚂蚁移动的指引作用.显然,带有新增启发式信息的蚂蚁构建的路径明显好一些.新增启发式信息使得算法在一开始迭代时就得到较好的解,这一点可从图 3看出.同时,由于解的质量较高,随后的信息素更新过程中,信息素能够在较短的路径上更快地积累,利于算法后期找到更好的解.第5次、第20次迭代时带有新增启发式信息的蚂蚁构建的路径明显也胜过只有一项启发式信息的蚂蚁.
新增启发式信息有利于得到更好的解主要原因是:仅带第一项启发式信息的蚂蚁构建路径选择下一个节点时,蚂蚁以较大概率选择距当前点近的节点,但并不知道距当前节点距离最近的点是否也距起点比较近,因此,蚂蚁移动的方向并不确定,容易造成转圈的路线.而具有新增启发式信息的蚂蚁在构建路径时,移动的方向明显确定,整体上是从起点指向终点的方向,蚂蚁的移动始终是不断靠近终点,所以整体路径的长度较短.第二项启发式信息在蚂蚁构建路径过程中起的主要作用是指引一条移动的大致方向,使得蚂蚁移动时尽可能不偏离这个方向,所以整条路径的长度更短.
4.3 MACO算法性能测试为了验证MACO的性能,从结果精度、收敛速度和运行时间方面将MACO与ACO进行比较.在本文实验中, 为了公平比较,对于两种算法共同的参数根据文献[12]给出的参考取值范围来设置,这些参数分别是:群体个数设为10,信息素权重α=1、启发式信息β=2、蒸发率ρ=0.05.MACO算法增加的参数γ的取值将影响到它的执行效率,第4.4节中将对该参数进行详细分析,在此先设为5.比较多种演化算法一般采用设置相同的适应度函数最大评估次数.本文比较的两种算法,蚂蚁构建路径的总长度是其适应度函数.在相同的种群个数和迭代次数下,这两种算法的适应度函数评估次数也是相同的.因此,本文实验将循环终止条件设为到达最大迭代次数,取值200.
表 1中是两种算法所得路径长度,其中Best、Mean、SD和Worst是算法独立运行20次所得的最优路径长度的最小值、平均值、标准方差和最大值.为了便于比较,Best、Mean和Worst中数据都四舍五入到个位,SD中的数据四舍五入到小数点后两位.本文采用Wilcoxon秩和检验方法对实验结果进行统计分析.该方法常用于演化算法之间的比较[15],它使得两种算法结果的比较具有统计意义.显著性水平设为0.05,统计结果记录在Wilcoxon列.
| Case | MACO | ACO | Wilcoxon | |||||||
| Best | Mean | SD | Worst | Best | Mean | SD | Worst | |||
| node10 | 303 | 303 | 0 | 303 | 303 | 303 | 0 | 303 | ≈ | |
| node20 | 323 | 323 | 0 | 323 | 323 | 328 | 4.00 | 333 | + | |
| node30 | 430 | 431 | 1.73 | 437 | 430 | 440 | 9.85 | 459 | + | |
| node45 | 523 | 541 | 11.23 | 571 | 523 | 548 | 14.21 | 581 | + | |
| node60 | 604 | 617 | 8.89 | 640 | 642 | 679 | 24.96 | 723 | + | |
| bays29 | 8 260 | 8 456 | 142.81 | 8 741 | 9 077 | 9 825 | 411.90 | 10 582 | + | |
| eil51 | 415 | 423 | 4.12 | 429 | 423 | 439 | 9.64 | 456 | + | |
| berlin52 | 8 045 | 9 438 | 14.53 | 9 943 | 11 501 | 12 181 | 332.27 | 12 737 | + | |
| st70 | 655 | 724 | 28.91 | 782 | 724 | 782 | 31.95 | 848 | + | |
| 注:“+”、“≈”分别表示MACO的性能优于、相当于ACO | ||||||||||
从表 1可以看出,node10算例上两种算法均得到相等的最优解、平均解、方差和最差解.而其他8个算例上,MACO算法的结果都显著优于ACO算法的结果,这一点除了从最优解、平均解、最差解上可以看出,从Wilcoxon秩和检验的结果上也可以看出.具体而言,在node20、node30和node45上,MACO和ACO都找到了相同的最优解,但是MACO在平均解、最差解上均优于ACO.在node60、bays29、eil51、berlin52和st70上,MACO的最优解、平均解和最差解上都远胜ACO.这说明增加的启发式信息使得MACO算法能够获得更优的解.从标准方差可以看出,MACO的结果更集中,说明了MACO更稳定.
对表 1的数据进一步分析,采用DACOi和DMACOi分别表示ACO算法和MACO算法路径长度,其中i∈{best, mean, worst},分别对平均解、最优解和最差解这三列的数据作如下计算
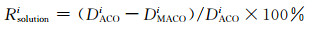
|
(6) |
结果记录到表 2中.
| % | |||
| Case | Mean | Best | Worst |
| node10 | 0 | 0 | 0 |
| node20 | 1.52 | 0 | 3.0 |
| node30 | 2.05 | 0 | 4.79 |
| node45 | 1.28 | 0 | 1.72 |
| node60 | 9.13 | 5.92 | 11.48 |
| bays29 | 13.93 | 9.00 | 17.40 |
| eil51 | 3.64 | 1.89 | 5.92 |
| berlin52 | 22.52 | 30.05 | 21.94 |
| st70 | 7.42 | 9.53 | 7.78 |
从表 2可以看出,节点数小于50时,MACO与ACO找到的最优解相同,平均解和最差解上MACO相对于ACO节省了不到5%的路径长度.但当节点个数在50到70之间时,MACO节省的路径长度大大增加.平均解上最大到达22.52%,最优解上最大到达30.05%,最差解上最大到达21.94%.可见,随着节点个数增多,MACO算法中增加的启发式信息带来的优势增大.
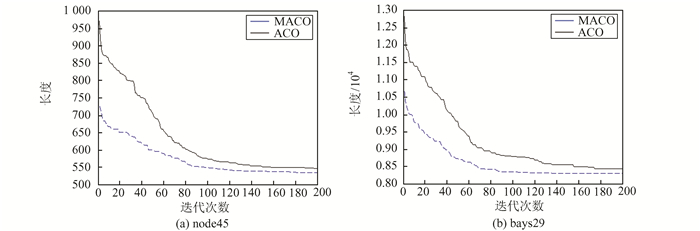
图 4描述了两种算法在算例node45和bays29上的收敛曲线.可以看出,MACO算法收敛速度较快,求解精度也较高.这是因为算法刚开始的时候,每条边上的初始信息素都是一样,信息素对路径构建的作用还未显示出来.此时启发式信息对路径的构建起了主要的作用,MACO利用两种启发式信息构建出比ACO更好的路径,这就是图 4中MACO比ACO一开始就能够找到质量更好的解的原因.这也说明了新增启发式信息是有效的.
|
| 图 4 两种算法的收敛曲线 Figure 4 Convergence curves of the two algorithms |
表 3是两种算法运行时间比较.其中,平均时间是算法运行20次的总时间除以20,单位是s.R表示MACO与ACO运行平均时间的比率,即R= 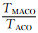
| Case | TMACO/s | TACO/s | R |
| node10 | 1.829 9 | 1.813 5 | 1.009 |
| node20 | 4.227 7 | 4.164 1 | 1.015 |
| node30 | 6.719 9 | 6.610 4 | 1.017 |
| node45 | 10.526 4 | 10.217 5 | 1.030 |
| node60 | 14.429 8 | 13.894 0 | 1.039 |
| bays29 | 6.520 6 | 6.351 6 | 1.027 |
| eil51 | 12.158 1 | 11.727 9 | 1.037 |
| berlin52 | 12.432 9 | 12.052 2 | 1.031 |
| st70 | 17.596 6 | 16.873 7 | 1.043 |
表 3中,MACO算法的平均运行时间与ACO算法的平均运行时间之比值在区间[1.009, 1.043],两种算法的平均运行时间差距不大.
综上所述,对于取样送检路径规划问题,本文新增的启发式信息是有效的,MACO算法求解质量和收敛速度均胜过ACO算法.
4.4 参数分析好的参数组合能够保持算法搜索的平衡性,使得算法不会把搜索范围收缩得过小而陷入停滞状态,也不会使搜索过程缺乏足够的指引,导致搜索范围过大而产生过量的探索.为了探讨γ对MACO算法性能的影响,以node30为算例,本文采用γ∈{1, 2, 3, 4, 5}来执行MACO算法,其他参数设置保持不变.γ取不同的值时MACO算法都独立运行20次,所得的解组成的矩阵记为xkt,其中k表示运行次数,t表示迭代次数.对每一个γ值,20次独立运行的平均解记为xtr,其中r表示γ的某个取值,则当γ取某个值时平均解相对于最优解的相对偏差RDtr的计算公式如下:

|
(7) |
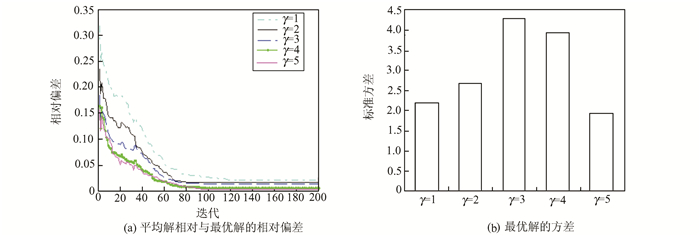
以相对偏差来反映结果的优劣,相对偏差的曲线图见图 5(a).以方差来反映算法的稳定性,当γ取不同值时算法找到的最优解的方差见图 5(b).从图 5可以看出,当γ=5时,所得的相对偏差最小,且方差也最小,此时MACO算法得到的解质量最高且稳定性最好.从这三个参数的值来看,即α=1、β=2和γ=5,新增启发式信息的权重大于信息素和第一项启发式信息的权重,这也验证了新增启发式信息在蚂蚁构建路径中的重要性.
|
| 图 5 γ对MACO算法的影响 Figure 5 The influence of γ on the MACO algorithm |
ACO算法提供了一种求解组合优化问题的通用框架.在实际应用中,可以根据具体应用的特点在该框架下增加合适的启发式信息.取样送检路径规划问题是一种带约束的组合优化问题.本文对取样路径优化问题进行了分析并给出其数学描述.为有效求解取样路径优化问题,提出了多启发式信息蚁群优化算法MACO,对MACO算法的收敛性进行了分析;详细地分析了新增启发式信息的作用,验证了该项启发式信息的有效性.9个算例测试结果表明,MACO算法求解取样路径优化问题比ACO算法收敛速度更快,求解精度更高.本文算法为取样送检路径规划问题提供了有效解决方法.
| [1] |
COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies[C]//Proceedings of the First European Conference on Artificial Life. Amsterdam(Dutch):Elsevier, 1991:134-142.
|
| [2] |
DORIGO M, GAMBARDELLA L M. Ant colony system:A cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 53-66. DOI:10.1109/4235.585892 |
| [3] |
DORIGO M, BIRATTARI M, STÜTZLE T. Ant colony optimization[J]. Computational Intelligence Magazine, IEEE, 2006, 1(4): 28-39. DOI:10.1109/MCI.2006.329691 |
| [4] |
MOHAN B C, BASKARAN R. A survey:Ant colony optimization based recent research and implementation on several engineering domain[J]. Expert Systems with Applications, 2012, 39(4): 4618-4627. DOI:10.1016/j.eswa.2011.09.076 |
| [5] |
BOUSSAÏD I, LEPAGNOT J, SIARRY P. A survey on optimization metaheuristics[J]. Information Sciences, 2013, 237: 82-117. DOI:10.1016/j.ins.2013.02.041 |
| [6] |
赵友虎, 刘聪, 张贺全. 济钢45 t转炉炼钢精益管理实践[J]. 山东冶金, 2015, 37(3): 57-58. ZHAO Y H, LIU C, ZHANG H Q. Lean management practice of 45 t converter steelmaking in Jinan Iron and Steel[J]. Shangdong Metallurgy, 2015, 37(3): 57-58. DOI:10.16727/j.cnki.issn1004-4620.2015.03.030 |
| [7] |
顾险峰, 焦剑. 海关取样工作的现状及路径创新[J]. 上海海关学院学报, 2008, 29(1): 44-49. GU X F, JIAO J. The status of customs sampling and path innovation[J]. Journal of Shanghai Customs College, 2008, 29(1): 44-49. |
| [8] |
APPLEGATE D L. The Traveling Salesman Problem:A Computational Study[M]. New Jersey: Princeton University Press, 2011: 1-5.
|
| [9] |
STÜTZLE T, LÓPEZ-IBÁNEZ M, PELLEGRINI P, et al. Parameter Adaptation in Ant Colony Optimization[M]. Berlin Heidelberg: Springer, 2012: 191-215.
|
| [10] |
CHANDRA B, KARLOFF H, TOVEY C. New results on the old k-opt algorithm for the traveling salesman problem[J]. SIAM Journal on Computing, 1999, 28(6): 1998-2029. DOI:10.1137/S0097539793251244 |
| [11] |
STÜTZLE T, DORIGO M. A short convergence proof for a class of ant colony optimization algorithms[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(4): 358-365. DOI:10.1109/TEVC.2002.802444 |
| [12] |
刘彦鹏. 蚁群优化算法的理论研究及其应用[D]. 杭州: 浙江大学. 2007. LIU Y P. Research on Ant Colony Optimization and Its Application[D]. Hangzhou:Zhejiang University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10335-2007079093.htm |
| [13] |
苏兆品, 蒋建国, 梁昌勇, 等. 蚁群算法的几乎处处强收敛性分析[J]. 电子学报, 2009, 37(8): 1646-1650. SU Z P, JIANG J G, LIANG C Y, et al. An almost everywhere strong convergence proof for a class of ant colony algorithms[J]. Acta Electronica Sinica, 2009, 37(8): 1646-1650. |
| [14] |
GERHARD R. TSPLIB[EB/OL].[2016-12-19]. http://elib.zib.de/pub/Packages/mp-testdata/tsp/tsplib/tsplib.html.
|
| [15] |
DERRAC J, GARCÍA S, MOLINA D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(1): 3-18. DOI:10.1016/j.swevo.2011.02.002 |
 2017, Vol. 63
2017, Vol. 63





