文章信息
- 肖江洪, 陈泽宗, 赵晨, 陈曦
- XIAO Jianghong, CHEN Zezong, ZHAO Chen, CHEN Xi
- 基于数据同化的高频地波雷达海流数据质量分析方法
- Quality Analysis Method of High Frequency Ground Wave Radar Current Data Based on Data Assimilation
- 武汉大学学报(理学版), 2017, 63(3): 213-218
- Journal of Wuhan University(Natural Science Edition), 2017, 63(3): 213-218
- http://dx.doi.org/10.14188/j.1671-8836.2017.03.004
-
文章历史
- 收稿日期:2016-05-16

2. 地球空间信息技术协同创新中心,湖北 武汉 430072
2. Collaborative Innovation Center for Geospatial Technology, Wuhan University, Wuhan 430072, Hubei, China
高频地波雷达(high frequency ground wave radar)利用垂直极化的高频电磁波,可大范围地探测海洋表面风浪流等海洋动力学参数,最远探测距离可达200 km[1].但由于大型岛屿遮挡、远距离回波衰减等因素的影响,非核心观测区域的数据质量较核心观测区域有所下降[2].传统验证高频雷达探测性能的方法是采用定点观测设备进行对比验证试验,如浮标、海流计、声学多普勒海流剖面仪(acoustic doppler current profilers, ADCP)等设备[2].这类方法分析雷达数据质量已取得了许多成果.朱大勇[2]总结了一些海流比测试验结果,并利用福建示范区的小浮标与ADCP的观测,对OSMAR2003地波雷达系统进行比测验证.结果表明,雷达与浮标观测比对误差较大,但在可接受范围内,而ADCP数据与雷达数据能较好地吻合.文献[2]还指出,定点比测验证方法会受到客观条件限制,且如何评价地波雷达的比测误差也没有统一的标准.李伦[3]利用高频地波雷达矢量流数据和ADCP观测的6个剖面矢量海流进行了比对,验证了雷达探测矢量流数据的有效性.然而,由于两者取样原理和探测深度不同,两种数据存在差异.Zhao等[4]利用2010年8月一次小型暴风雨中ADCP获取的海流数据与变频高频地波雷达在不同工作频段探测的径向流数据进行比测,结果表明,雷达获得的径向流数据与ADCP在距海平面2~4 m处探测得到海流数据结果高度相关.但由于定点设备只能探测以某点或多个点为代表区域海流数据,因此无法实现整个探测区域的比测.
定点设备比测方法虽能较为精确评估雷达数据质量,但不能判断整个探测区域的数据质量,且人力物力财力耗费巨大.为了弥补定点比测方法的缺陷,本文提出利用数据同化方法分析高频地波雷达数据质量.同化结果可以大范围地判断雷达获取数据质量,指导改善雷达探测性能.目前同化方法主要有逐步订正法[5](successive-correction method, SCM)、三维变分法[6](three dimentional variational method, 3DVAR)、四维变分法[7](four dimensional variational Method, 4DVAR)、集合卡尔曼滤波法[8](ensemble kalman filter, ENKF)等[9, 10].国际利用数据同化方法分析东海区域的高频地波雷达数据质量处于起步阶段.本文尝试利用SCM,将东海区域高频地波雷达表面流数据同化到POM(princeton oceanic model)模型中,通过分析同化后数据与雷达原始数据的均方根误差RMSD(root-mean square deviation)分布,得到探测区域内雷达数据质量,为改善雷达的探测性能提供指导.
1 模型与方法 1.1 POM模型及参数设置POM模型是由美国普林斯顿大学大气海洋科学项目组研制的三维全动力海洋模式[11].该模型采用有限差分法进行计算,结构简单,计算速度快.水平方向采用正交曲线坐标,参数布置采用交错网格(Arakawa C),时间差分为显格式;垂直方向采用σ坐标,时间差分为隐格式;并采用模态分离方法简化计算[11].图 1中蓝色矩形区域为POM模型计算区域,范围为东经122.3°~125°,北纬28.5°~31.5°,将径向流合成海流区域完全覆盖.模型的水平计算网格采用均匀正交网格,空间分辨率为0.05°×0.05°,垂向分层为16层.模拟的地形数据采用ETOPO1全球地形数据集,开边界由TPXO7.2数据集中的8个主要分潮(M2、S2、N2、K2、K1、O1、P1、Q1) 和2个浅水分潮(M4、MS4) 的水位调和常数提供[12, 13],温度盐度分别设为20 ℃和20 psu.模式初始流场为0,从2015年10月1日00:00:00开始计算得到模型预测值.计算一个月达到稳定状态后,将高频地波雷达观测值同化到模型中得到同化值,再将同化结果输入到模型中,优化模型预测值.在模型计算达到稳定后,即从2015年11月1日00:00:00开始,每隔30 min输出一次模型预测值、同化值, 用于分析雷达数据质量.

|
| 图 1 雷达探测区域和模型模拟区域 Figure 1 Detection area of radar and simulation area of model |
变频高频地波雷达系统采用线性调频中断连续波(frequency modulated interrupted continuous wave, FMICW)体制,其工作参数如表 1所示.在实际应用中,针对不同的探测目的,可以从7.5~25 MHz的高频频段之中任选出4个频率点实现帧间变频、场间变频等方式,以满足风浪流探测的要求.根据不同的雷达频率,系统的距离分辨率控制在1~5 km之间,当电磁环境较好、回波干扰较小时,海流的最大探测距离可达200 km[1].发射天线向海洋表面发射电磁波,电磁波掠入射海面发生Bragg散射,天线接收回波,利用MUSIC(multiple signal classification, 多重信号分类)算法,每隔10 min进行反演得到径向海流数据,最后利用双基站数据合成得到海流数据[1, 4].图 1所示的红色扇形区为单基站雷达探测区域,重叠部分为径向流合成海流区.黄色圆点为雷达站点,其中泗眺站的经纬度为(29.9°N, 122.4°E),嵊山站的经纬度为(30.7°N, 122.8°E).本文采用的雷达数据为2015年11月1日00:00:00~2016年2月1日00:00:00嵊山-泗眺站合成的海流数据,时间间隔为10 min,空间范围为东经122.3°~125°,北纬28.5°~31.5°,数据网格分辨率为0.05°×0.05°.
| 参数 | 参数值 |
| 雷达工作方式 | 同时4频或分时4频,收发共站 |
| 雷达工作频率 | 7.5~25 MHz |
| 雷达发射机峰值功率 | ≤300 W |
| 距离分辨率 | 1~5 km可变 |
| 供电电源 | 220 V,50 Hz |
数据同化在客观分析的基础上采用迭代求解的方法,形成逐步订正法,现已广泛应用于各种气候诊断分析和数值模拟研究中.本文采用逐步订正法进行数据同化实验,将POM模拟海流场作为背景场,利用高频地波雷达观测数据进行逐步订正,直到得到的分析值逼近雷达数据为止.具体做法如下:
1) 给定初始场,第一次分析格点场来源于背景场,如(1) 式所示.
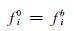
|
(1) |
其中,fib是格点i的背景场点,即POM预报场,fi0是相应第0次迭代的网格场分析值.
2) 用高频地波雷达数据逐步修正背景场,选取合适的迭代半径和订正次数,使订正后的分析场接近观测记录值.
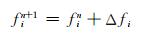
|
(2) |
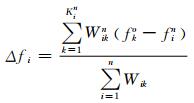
|
(3) |
其中,n为订正次数;Kin为第n次迭代时,以格点i为中心,位于影响半径内格点的数量;fin+1是第n次迭代后格点i的分析值;fko是在分析值fin周围第k个观测值;Wikn是第n次迭代时,第k个观测值的权重因子,取值在0~1之间,定义如下:
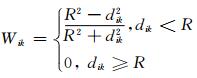
|
(4) |
dik是观测点dk到格点di的距离,单位为m. R是迭代半径,对于非常小的迭代半径,当观测值位于格点时,分析值收敛于观测值[8, 9].利用分析场与观测场空间平均的均方根误差RMSD值作为评判同化分析值是否收敛于观测值的指标,公式如下:
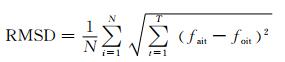
|
(5) |
其中,fait为t时刻格点i的同化分析值;foit为t时刻格点i的雷达数据值;N为总网格点数.当误差空间平均值小于一定值时,认为同化分析值收敛于观测值.RMSD是反映同化结果的重要因素,RMSD越小,同化结果越好;RMSD越大,同化结果越差.
迭代半径R的选取具有人为因素,一般选取原则是由小及大进行扫描.本文假设R为常数,由近及远逐次进行扫描订正.若订正次数越多,虽然分析的误差小,但耗费时间较长;若订正次数太少,虽然耗费时间较短,但分析场的误差较大.因此,需通过多次试验分析,选取合适的迭代半径和订正次数.
2 结果与分析 2.1 迭代半径和订正次数选取本文采用2015年11月1日00:00:00~2015年11月2日00:00:00的雷达数据,对不同的同化迭代半径R和订正次数n进行实验.通过分析订正结果的优劣和算法的耗时,选取合适的R和n.为了实验方便利用n=R/r,将实验的变量转换成R和r, 其中r为迭代半径增长步长.由于数值模型模拟网格分辨率与雷达网格分辨率都为0.05°×0.05°,为了保障每次递增半径都有新的观测数据加入,因此实验选取r为0.05°的整数倍.本文选取的实验迭代半径和迭代步长分别为:
R1=[0.05°, 0.1°, 0.15°, …, 0.6°],r1=0.05°
R2=[0.1°, 0.2°, 0.3°, …, 0.6°], r2=0.10°
R3=[0.15°, 0.3°, 0.45°, 0.6°], r3=0.15°
R4=[0.2°, 0.4°, 0.6°], r4=0.20°
R5=[0.25°, 0.5°], r5=0.25°
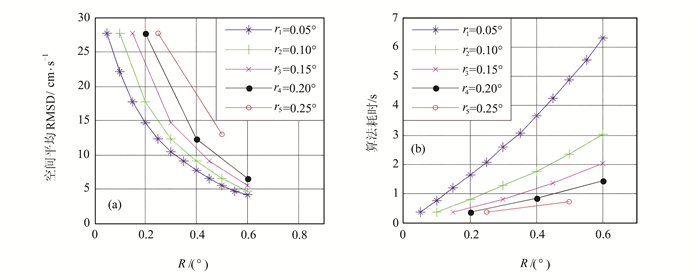
统计在不同迭代半径R、不同半径增长步长r下,分析值与观测值的空间平均RMSD和算法耗时的结果如图 2所示.
|
| 图 2 迭代次数对空间平均RMSD(a)和算法耗时(b)的影响分析 Figure 2 Analysis of the effect of the number of iterations on the RMSD (a) and algorithm time consuming (b) |
由图 2(a)可知,r不变时,分析场与观测场的空间平均RMSD,随着R的增加而减小;R不变时,空间平均RMSD随着r的增加而增大.由图 2(b)可知,r不变时,同化算法耗时随着R的增加而增长;R不变时,算法耗时随r的增大而减小.本文进行模型模拟时,由于模型边界条件主要由水位调和常数控制,未考虑风应力、温度、盐度对模型的影响,因此模拟值与观测值存在一定的误差.雷达数据与其他数据进行比测时,通常认为,雷达数据与比测数据之间的RMSD < 20 cm/s时[2],雷达数据质量可靠.因此,综合以上两点因素考虑,当同化后分析值与雷达观测值的空间平均RMSD < 20 cm/s时,认为同化值收敛于观测值,同化结果可靠.
综合考虑同化质量和算法消耗的时间,保证同化后RMSD在可靠范围内,同时又节省时间成本.因此本文选取同化迭代半径R=[0.05°, 0.10°, 0.15°, 0.20°, 0.25°],增长步长r=0.05°, 订正次数n=5次.
2.2 高频地波雷达数据质量分析通过统计高频地波雷达在探测区域内的数据获取率、时间序列均方差分布,分析高频地波雷达的数据质量, 如图 3, 图 4所示.

|
| 图 3 雷达数据获取率分布 Figure 3 Distribution of radar data acquisition rate |

|
| 图 4 雷达探测海流流速的时间序列均方差 Figure 4 Mean square error of radar detection current velocity time series |
图 3为2015年11月1日00:00:00~2016年2月1日00:00:00,高频地波雷达在探测区域内的数据获取率.黑线以内的区域,雷达数据获取率大于70%,能够有效地保证数据在时间、空间上的连续性.黑线以外的区域,数据获取率小于70%,部分地区甚至不足20%,雷达获取数据在时间、空间上不连续.
通过计算雷达探测海流流速的时间序列均方差,研究雷达数据的平稳性.计算公式如下:
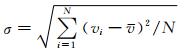
|
(6) |
其中,vi为第i时刻各网格点的海流流速值;v为各网格点海流流速时间序列的均值;N为各网格点时间序列的点数.由(6) 式计算得到的结果如图 4所示,由图可知,雷达探测海流流速的时间序列均方差分布与雷达数据获取率分布类似.图 4白线内区域的均方差小于15 cm/s,数据平稳可靠.白线外区域均方差较大,部分区域甚至超过100 cm/s,数据波动大,存在异常值.
雷达探测的核心区域位于获取海流数据量多且平稳的区域.综上所述,嵊山-泗眺雷达探测的核心区域为数据获取率大于70%,均方差小于15 cm/s的区域,其范围为东经122.6°~124°,北纬30.1°~31°,面积约为19 350 km2,离嵊山站的最远距离为144.4 km,离泗眺站的最远距离为175.2 km.
2.3 同化分析高频地波雷达数据质量模型模拟结果具有大范围、数据连续的优点,而雷达观测具有实时、准确的优点.数据同化方法结合了模型模拟与雷达实测的优点,通过同化算法能够得到更好的数据结果.同化值与雷达观测的RMSD是分析同化效果的重要依据.同化结果与模型精度、雷达数据质量有关,不考虑模型模拟精度的情况下,雷达数据质量越好,同化结果越好,得到的RMSD越小;反之,若雷达数据质量越差,同化结果也越差,得到的RMSD越大.
RMSD的计算公式如下:
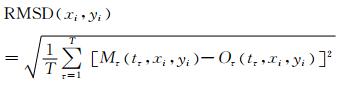
|
(7) |
其中,T是对比时间(s),(xi, yi)是模型网格点,Mτ(tτ, xi, yi)为同化后的海流流速值,Oτ(tτ, xi, yi)为高频雷达观测值.
根据前文所述,当RMSD < 20 cm/s时,同化结果收敛,雷达数据质量好.图 5为数据同化后海流流速的RMSD分布.对比图 3~图 5可得,同化后RMSD分布与雷达数据获取率、雷达探测海流流速均方差分布类似.通过实验测试得到,白线内区域同化后的RMSD小于20 cm/s,与前文分析得到的雷达核心区域相近.范围为东经122.6°~124.3°,北纬29.7°~31.1°,面积约为20 123 km2的区域;区域内距嵊山站的最远距离为146.6 km,距泗眺站的最远距离为206.4 km.白线外区域同化后的RMSD较大,部分地区甚至超过40 cm/s.对比图 3和图 4可知,通过数据同化结果,能够正确评价雷达数据质量.同化3个月的雷达数据耗时约为15 min,大幅减少了雷达数据质量分析的时间成本.同时,同化方法只需计算模拟,不需借助观测设备数据进行出海实验获得比测,大大减少了运行成本.

|
| 图 5 数据同化后海流流速的RMSD分布 Figure 5 The RMSD distribution of current velocity after data assimilation |
通过相关性分析,进一步定量分析同化后RMSD分布与雷达数据质量关系,计算公式如下:
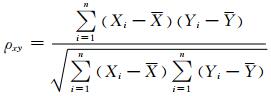
|
(8) |
其中,Xi为参数X在网格点i的值; X为参数X在所有网格点值的均值;Yi为参数Y在网格点i的值;Y为参数Y在所有网格点值的均值.由(8) 式计算得到,同化后RMSD与雷达数据获取率、雷达数据均方差的相关系数分别为-0.65和0.59,具有较强的相关性.
图 6、图 7分别为同化后RMSD与雷达数据获取率、雷达数据均方差的相关系数散点分布图.由图 6、图 7可知,同化后RMSD分布与雷达数据获取率负相关,与数据均方差正相关.数据获取率越高、方差越小时,相关性越强;由于数据获取率越低、方差越大时,数据波动较大,出现异常值可能性较大,相关性变弱.通过相关性分析可知,同化后RMSD与雷达数据质量强相关,进一步验证了数据同化方法可有效判断雷达数据质量.

|
| 图 6 同化后RMSD与雷达数据获取率的相关性 Figure 6 Correlation coefficient between the RMSD after data assimilation and the rate of radar data acquisition |

|
| 图 7 同化后RMSD与海流流速均方差的相关性 Figure 7 Correlation coefficient between the RMSD after data assimilation and mean square error of radar data |
本文分析了迭代半径和订正次数对SCM同化结果的影响,选取了合适的订正条件进行同化实验.利用SCM法,将高频地波雷达观测得到的海洋表面流数据同化到POM模型中.根据同化后数据与雷达原始数据的RMSD分布,判断得到泗眺-嵊山雷达站点的探测核心区域位于同化后RMSD < 20 cm/s的区域.实验结果表明,利用数据同化方法能大范围、高效地判断高频地波数据质量,并耗费较少的人力财力物力和时间,可望为提高高频地波雷达探测性能提供很好的指导.
随着数据同化算法的深入研究,许多新的同化方法被提出,如3DVAR、4DVAR、集合卡尔曼滤波法等.今后的工作应着重于研究更先进的同化算法,更好地指导改善雷达探测性能.
| [1] |
赵晨. 变频高频地波雷达海态反演技术的研究与应用[D]. 武汉: 武汉大学, 2012. ZHAO C.Research and Application of Multi-frequency HF Ground Wave Radar Sea State Inversion Technology[D]. Wuhan: Wuhan University, 2012(Ch). |
| [2] |
朱大勇. 高频地波雷达在近海区域的应用研究——以台湾海峡为例[D]. 厦门: 厦门大学, 2008. ZHU D Y.Applications of High Frequency Ground Wave Radar to Coastal Ocean——A Case Study in the Taiwan Strait[D]. Xiamen: Xiamen University, 2008(Ch). |
| [3] |
李伦. 高频地波雷达海洋动力学参数反演与应用方法研究[D]. 武汉: 武汉大学, 2013. LI L.Ocean Dynamic Parameters Inversion and Application Method with High Frequency Surface Wave Radar[D]. Wuhan: Wuhan University, 2013(Ch). |
| [4] |
ZHAO C, CHEN Z Z, ZENG G F, et al. Evaluating radial current measurement of Multifrequency HF radar with multidepth ADCP data during a small storm[J]. Plant Disease, 2015, 32(5): 154-158. DOI:10.1175/JTECH-D-14-00037.1 |
| [5] |
SINHA S K, TALWALKAR D R, RAJAMANI S. On some aspect of objective analysis of humidity over Indian region by the optimum interpolation method[J]. Advances in Atmospheric Sciences, 1987, 3: 332-342. DOI:10.1007/BF02663603 |
| [6] |
ZHU J, ZHOU G Q, YAN C Z. A three-dimensional variational ocean data assimilation system: Scheme and preliminary results[J]. Science in China(Series D: Earth Sciences), 2006, 11: 1212-1222. DOI:10.1007/s11430-006-1212-9 |
| [7] |
MICHAUD C. A 4DVAR system for the Navy Coastal Ocean Model. Part Ⅱ: Strong and weak constraint assimilation experiments with real observations in Monterey Bay *[J]. Monthly Weather Review, 2014, 142(6): 2108-2117. DOI:10.1175/MWR-D-13-00221.1 |
| [8] |
PADUAN J D, SHULAMN I. HF radar data assimilation in the Monterey Bay area[J]. Journal of Geophysical Research Oceans, 2004, 109(C7): 259-265. DOI:10.1029/2003JC001949 |
| [9] |
马寨璞, 井爱芹. 海洋科学中的数据同化方法——意义、结构与发展现状[J]. 海岸工程, 2005, 24(4): 83-99. MA Z P, JING A Q. Data assimilation method applied in marine science — Its significance, system configuration and development situation[J]. Coastal Engineering, 2005, 24(4): 83-99. DOI:10.3969/j.issn.1002-3682.2005.04.012 |
| [10] |
LIANG K, BLUMBWEG A F, GEORGAS N. Impact of assimilating high frequency radar surface currents on the fidelity of a Middle Atlantic Bight circulation model[C]//Oceans, 2012. New York: IEEE Press, 2012:1-9. DOI:10.1109/OCEANS.2012.6405054.
|
| [11] |
郑沛楠, 宋军, 张芳苒, 等. 常用海洋数值模式简介[J]. 海洋预报, 2008, 4: 108-120. ZHENG P N, SONG J, ZHANG F R, et al. Common instruction of some ogcm[J]. Marine Forecasts, 2008, 4: 108-120. DOI:10.3969/j.issn.1003-0239.2008.04.016 |
| [12] |
史军强. 长江口近海数值模拟及地波雷达数据同化研究[D]. 青岛: 中国海洋大学, 2014. SHI J Q.Numerical Simulation and HF-Radar Data Assimilation Research Near the Changjiang River Estuary[D]. Qingdao: Ocean University of China, 2014(Ch). |
| [13] |
陈金瑞. 胶州湾及青岛近海岸线变迁对青岛近海海洋动力环境的影响研究[D]. 青岛: 中国海洋大学, 2011. CHEN J R.The Research on the Impact of Dynamic Environment in Qingdao Adjacent Sea Due to the Change of Costal Line in Jiaozhou Bay and Qingdao Adjacent Sea[D]. Qingdao: Ocean University of China, 2011(Ch). |
 2017, Vol. 63
2017, Vol. 63





