0 引言

本文研究一类同时具有非线性阻尼项和多个非线性源项的波动方程的初边值问题，具体形式如下:

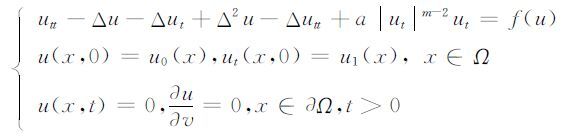
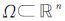
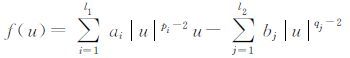
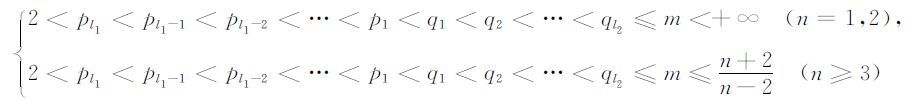
其中为有界光滑区域，a为正常数，整数m>2，非线性源项u，这里常数a_i,b_j≥0,p_i,q_j满足：

(4)

具有阻尼项的非线性波动方程是一类非常重要的波动方程，它们是从具有黏性效应物体的运动中提出的，阻尼是指阻碍物体的相对运动并把运动能量转化为热能或其他可以耗散能量的一种作用.阻尼现象广泛存在于自然界中，例如弹性杆的纵向运动、具有表面张力的水波运动以及导体在变化的磁场中运动等都包含阻尼现象.近年来，越来越多的学者开始研究不同类型的波动方程解的存在惟一性问题，能量估计法是最重要的分析工具之一，研究表明对于含有正定能量的波动方u_tt－Δu=－|u|^p－1u，利用Gakerkin近似解法可以有效解决，当方程含有非正定能量时，仅用该方法不能解决.1968年Sattinger通过位势井方法研究了含有非正定能量的波动方程整体解的存在性^[1].1975年，Payne和Sattinger证明不具有正定能量的波动方程u_tt－Δu=|u|^p－1u整体解的存在性与爆破现象^[2]，2007年叶朝辉分析了具有两个异号源项的波动方程u_tt－Δu+a|u|^p－1u－b|u|^q－1u=0整体弱解的存在性^[3]，卞春雨和白云成将上述方程推广到含有弱项阻尼项au_t的高阶波动方程，并得到了整体弱解的存在惟一性^[4].另外沈继红证明了含有强阻尼项aΔu_t高维广义Boussmesq方程整体解的存在性与不存在性的门槛结果^[5].文献^[6]针对非线性阻尼进行了讨论.

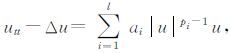
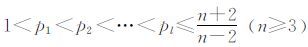
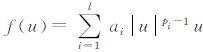
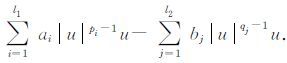
最近刘亚成^[7]给出了如下含有多个非线性源项的波动方程其中a_i>0,p_i满足：1 ＜p₁＜p₂＜…＜p_l＜∞ n=1,2或，作者利用位势井理论并结合凸性方法得到了整体解的存在惟一性，并对解的真空隔离现象进行了分析.2011年徐润章^[8]将上述方程推广至如下具有组合型非线性源项的波动方程u_tt－u_xx+u_xxxx+f(u)_xx=0，其中或而且常数a_i,b_j>0,参数p_i,q_j满足类似公式(4)的条件，作者利用一种新的分析技巧，研究了整体解的存在惟一性与爆破现象.

需要指出的是上述大部分结论都没有考虑阻尼项对波动方程的影响，虽然文献^[4]和^[5]研究两种不同阻尼形式对波动方程的影响，但他们给出的阻尼项都是线性的，当阻尼项具有非线性形式au_t^m－2u_t时^[6]，他们的分析方法将不再适用.目前，对于同时含有非线性阻尼项和多个源项的波动方程(1)~(4)还未有任何结论，最近文献^[9]证明了一类含有非线性阻尼和单个源项的波动方程整体解的存在性，本文将文献^[7~9]结论推广到含有多个源项的情况，并分析同时含有非线性阻尼与多个源项的波动方程的整体解的存在性与渐近稳定性.

1 主要引理

为了计算方便，引入下面记号

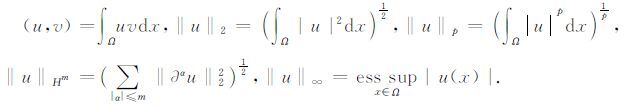
为了得到文本的结果，引入下面范数

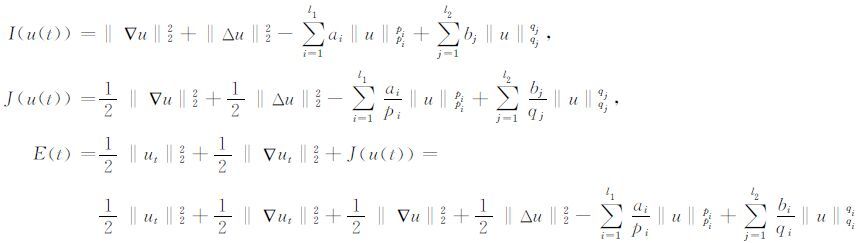
和集合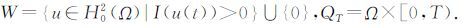

定义1 若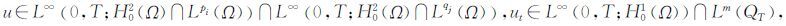并且满足：

(i) 对任意函数v∈H₀²(Ω)∩L^m(Ω)和a.e.0≤t ＜T，有

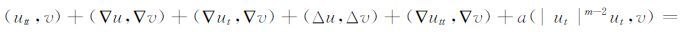
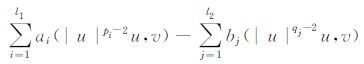
(ii) u(x,0)=u₀(x)在H₀²(Ω)∩L^m(Ω)中，u_t(x,0)=u₁(x)在H₀¹(Ω)∩L^m(Ω)中.

则称u(x,t)为方程(1)~(3)的弱解.

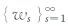
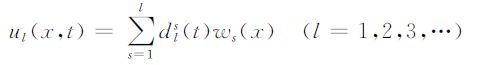
记为空间H₀²(Ω)∩L^m(Ω)的基函数系，利用Galerkin方法构造方程(1)~(4)的近似解

(5)

其中d_l^s(t)满足如下常微分方程系统：

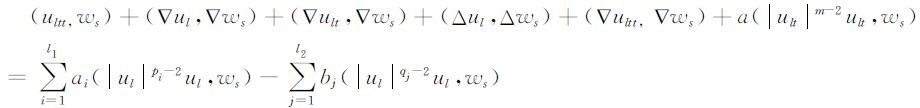
(6)

,在H₀²(Ω)∩L^m(Ω)中，

,在H₀¹(Ω)∩L^m(Ω)中.

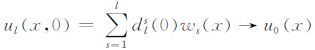
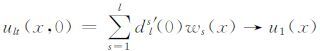
将方程(6)两边同乘以d_l^s(t)′并求和可得

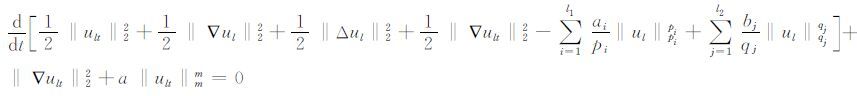
(7)

为了研究方程(1)整体弱解的存在性，下面给出本文的主要引理.

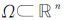
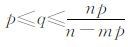
引理1^[10] (Sobolev嵌入定理)设有界且有锥性质，如果mp ＜n，有H^m,p(Ω)嵌入L^q(Ω)，其中；如果mp=n，有H^m,p(Ω)嵌入L^q(Ω),其中p≤q＜∞.

引理2^[9] 设函数u(x,t)∈L^∞0,T;H₀²(Ω)，u_t(x,t)∈L^∞(0,T;H₀¹(Ω))∩L^m(Q_T)，u(x,0)=u₀(x)，u_t(x,0)=u₁(x)，如果u_tt－Δu－Δu_t+Δ²u－Δu_tt=h，其中

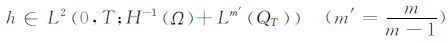
那么对任意0 ＜t ＜T有

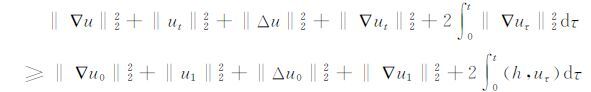
(8)

引理3^[9] 如果函数列u_it满足:

(i) u_it→u_t在L^mQ_T中弱收敛.

(ii) a|u_it|^m－2u_it→ξ在L^m′Q_T中弱收敛，其中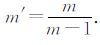

(iii) 对任意0 ＜t＜T，有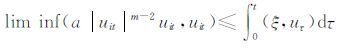

则ξ=a|u_t|^m－2u_t.

2 整体弱解的存在性

在这一部分，主要讨论方程(1)~(4)的整体弱解的存在性.

定理1 设u₀(x)∈H₀²(Ω)∩L^m(Ω)，u₁(x)∈H₀¹(Ω)∩L^m(Ω)，则对任意T>0，方程(1)~(4)存在一个整体弱解u(x,t),且u_t(x,t)∈L^∞0,T;H₀¹(Ω))∩L^m(Q_T)，u(x,t)∈L^∞0,T;H₀²(Ω)∩L^p_i(Ω)和u(x,t)∈L^∞0,T;H₀²(Ω)∩L^q_j(Ω).

证将方程(7)两边积分可得

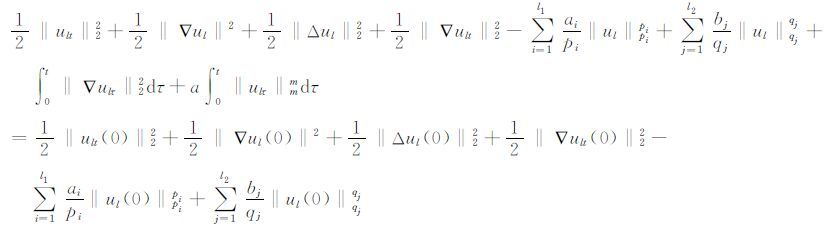
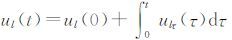
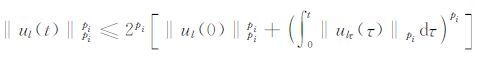
利用和Minkowskal不等式可得：

再利用Holder不等式得：

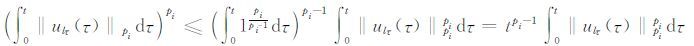
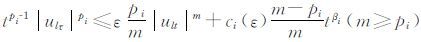
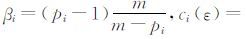
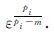
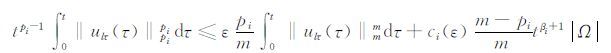
由Young不等式可知：其中所以

于是经过计算后得：

选择ε使得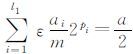可得：

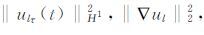
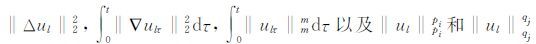
利用公式(4)以及方程(6)的初始条件可知，M(T)是仅与T有关的常数，从而都是有限的，它们被仅与T有关的常数控制，因此u_l∈L^∞0,T;H₀²Ω∩L^p_iΩ，u_l∈L^∞(0,T;H₀²(Ω)∩L^q_j(Ω))和u_lt∈L^∞(0,T;H₀¹(Ω)∩L^m(Q_T)).

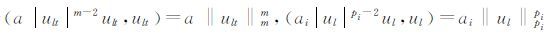
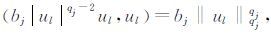
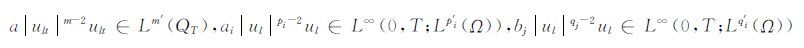
由于和 所以

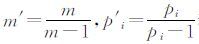
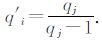
其中和

于是可以选取{u_l}的子数列{u_v}，当u_v→∞时，可得：

u_v→u 在L^∞0,T;H₀²Ω∩L^p_iΩ和L^∞0,T;H₀²Ω∩L^q_jΩ上弱*收敛，

u_v→u 在Q_T=Ω×[0,T)上几乎处处收敛，

u_vt→u_t 在L^∞0,T;H₀¹Ω上弱*收敛，

u_vt→u_t 在L^m(Q_T)上弱收敛，

a|u_vt|^m－2u_vt→ξ在L^m′(Q_T)上弱收敛.

利用文献^[11]中的Lions引理可知，对任意i=1,2,…,l₁和j=1,2,…,l₂有

a_i|u_v|^p_i－2u_v→a_iu^p_i－2u 在L^∞0,T;L^p′_iΩ上弱*收敛，

b_j|u_v|^q_j－2u_v→b_ju^q_j－2u 在L^∞0,T;L^q′_jΩ上弱*收敛.

对(6)式先从0到t积分，然后取v→∞，再对t微分可得

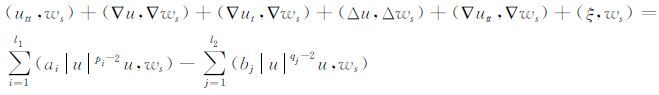
选取v(x)∈H₀²(Ω)∩L^m(Ω)，由w_s(x)在H₀²(Ω)∩L^m(Ω)中稠密可得v(x)=∑∞s=1d_sw_s(x),其中d_s为给定的函数，所以对任意v(x)∈H₀²(Ω)∩L^m(Ω)有

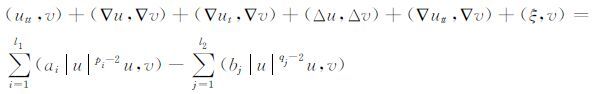
(9)

下证ξ=a|u_t|^m－2u_t，记g(s)=a|s^m－2|s，从(6)式可得

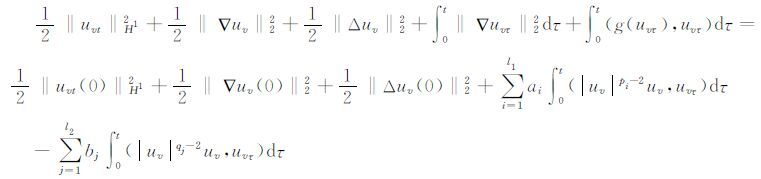
令v→∞得

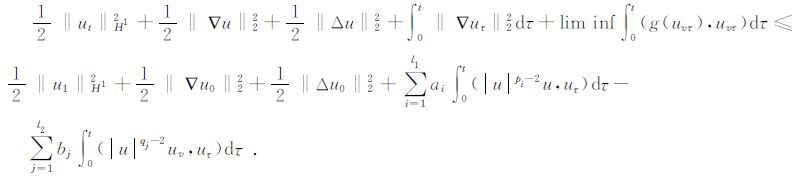
利用引理2中的公式(8)可得

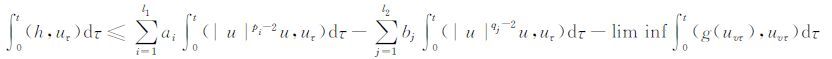
由条件(4)可得m′ ＜p′_l1＜…＜p′₁＜q′₁＜…＜q′_l2，于是

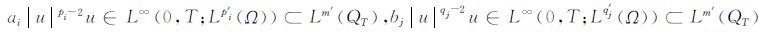
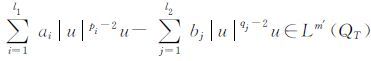
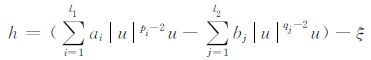
所以，从引理2知h∈L²(0,T;H^－1(Ω)+L^m′(Q_T))，可取

使得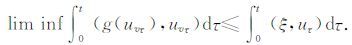由引理3可得ξ=a|u_t|^m－2u_t.于是由公式(9)可得方程(1)~(4)存在一个整体弱解.

3 弱解的渐近稳定性

为了得到整体弱解的渐近稳定性，首先给出下面引理.

引理4^[9] 如果u(x,t)为方程(1)~(4)的解，则能量泛函E(t)满足：

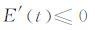
(10)

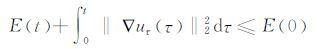
(11)

引理5 设(u₀,u₁)∈W×H₀¹Ω，在条件(4)下，如果b_j=0(j=1,2,…,l₂)且

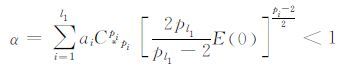
(12)

其中C_*pi是H₀¹(Ω)嵌入到L^p_i(Ω)的Sobolev常数，则方程(1)~(3)的整体弱解u(t)∈W.

证 由于I(u₀)>0且I(ut)关于时间连续，所以存在t₁>0，使得对任意0≤t≤t₁，有I(u(t))>0，于是当b_j=0时有

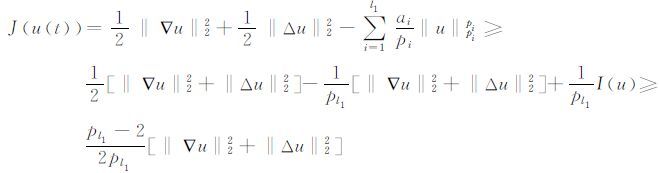
所以对任意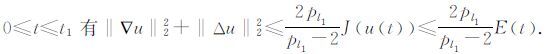

利用引理4可知

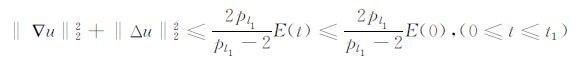
(13)

如果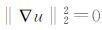，利用u∈H₀²(Ω)可得u=0，从而u∈W；

如果，利用引理1和公式(12)可得

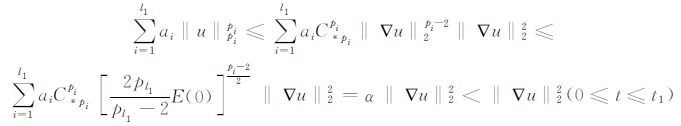
(14)

其中C_*pi为H₀¹(Ω)到L^p_i(Ω)的Sobolev常数，即对任意0≤t≤t₁有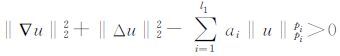所以u∈W，重复上面的步骤可知对任意0≤t ＜T，有u(t)∈W.

引理6 在引理5的条件下，方程(1)~(3)的整体弱解满足‖u(t)‖_m^m≤LE(t),其中

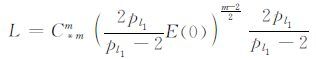
证 仿照引理5的证明过程可得

引理7 在引理5的条件下，设

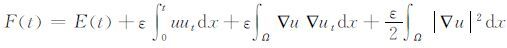
则对任意u∈W，存在常数C₁，C₂>0，使得当ε足够小时有C₁E(t)≤F(t)≤C₂E(t).

证由于p_i满足条件(4)，所以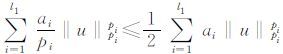，利用文献^[9]类似的估计方法即可得到结论.

定理2 设(u₀,u₁)∈W×H₀¹(Ω)，在引理5的条件下，存在常数M,k>0,使得方程(1)~(4)的整体弱解满足E(t)≤Me^－kt(t≥0).

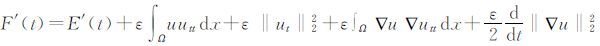
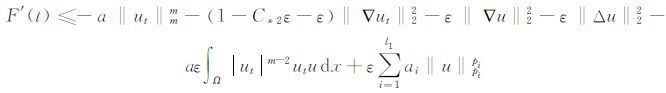
证 由F(t)的定义得，利用方程(1)和引理4，并结合Poincare不等式可得

对于常数λ>0，利用能量泛函E(t)的定义以及公式(14)可知：

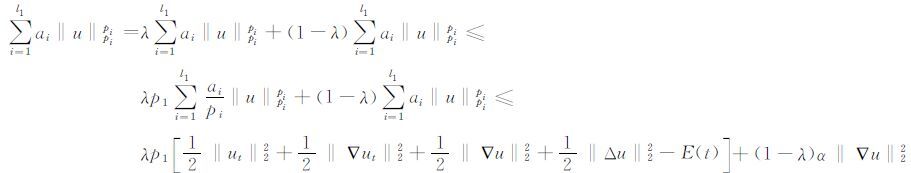
最后结合引理6并使用文献^[9]类似的方法可得存在常数k>0，使得F′(t)≤kF(t)，由Gronwall等式可知F(t)≤F(0)e^－kt，由引理7可知，存在常数M>0，使得：E(t)≤Me^－kt(t>0).