文章信息
- 王丽娜, 徐一波, 翟黎明, 任延珍
- WANG Lina, XU Yibo, ZHAI Liming, REN Yanzhen
- 基于熵的视频运动矢量隐写分析算法
- Motion Vector Steganalysis Algorithm Based on Entropy
- 武汉大学学报(理学版), 2017, 63(5): 427-433
- Journal of Wuhan University(Natural Science Edition), 2017, 63(5): 427-433
- http://dx.doi.org/10.14188/j.1671-8836.2017.05.007
-
文章历史
- 收稿日期:2016-08-12

2. 武汉大学 计算机学院, 湖北 武汉 430072
2. School of Computer, Wuhan University, Wuhan 430072, Hubei, China
隐写(信息隐藏)可以将信息嵌入载体实现信息秘密传递.隐写载体可以是文本、图像、视频、音频等常见数字媒体.众多类型的隐写术中,以数字图像为载体的信息隐藏研究开展最为广泛[1],而以数字视频为载体的隐写术近年来也开始得到关注[2].
视频隐写术一般包括视频空域隐写,视频频域隐写以及运动矢量隐写几种[2].其中,基于运动矢量的隐写具有隐藏容量大,画面失真小以及嵌入过程简单等优点.早期的运动矢量隐写算法较关注视频画面保真:如Xu等[3]认为选择运动矢量中绝对值较大的分量进行LSB(lest significant bit,最低有效位)隐写能够保证较小的失真.Aly[4]则通过峰值信噪比选择残差能量更大的块隐写保持画面质量,也可保持较小的码率增长.和Xu方法每个运动矢量仅可嵌入1比特信息相比,Aly方法可以做到每个运动矢量嵌入2比特秘密信息.近期运动矢量隐写在失真模型和编码技术上的应用使得画面质量和安全性都有提升:Cao等[5]通过次优运动矢量替换最优运动矢量的方法嵌入秘密信息.该方法使用湿纸编码技术跳过不满足候选运动矢量条件的湿点宏块得以实现.而随着STC(syndrome-tellis codes)编码[6]在信息隐藏中的应用,隐写算法的安全性得到了一次飞跃性的提升:Cao等[7]使用STC和湿纸双层编码,设计了一种可以较好保持运动矢量局部最优的隐写算法.Zhang等[8]为了进一步克服局部最优异常,提出一种使用具有局部最优性的候选运动矢量进行隐写替换的MVMPLO(motion vector modification with preserved local optimality)算法.Yao等[9]则设计运动矢量相关性和局部最优性的融合失真代价,结合STC做到运动矢量失真最小.
运动矢量隐写分析特征大致可以分为两类,第一类是相关性特征,可以描述运动矢量的分量数值在空域或时域上相关性;另一类则是最优性特征,可以描述运动矢量局部编码代价最优性.第一类特征代表是Su等[10]提出的特征,利用运动矢量直方图的中心距分别从空域和时域构造特征进行隐写分析.第二类特征则是包括15维的Cao等[11]提出的特征,利用重压缩视频残差进行校准设计.除这些特征以外,Wang等[12]利用运动矢量指向最优参考块特性,提出了18维的AoSO特征.该特征统计运动矢量及其8个邻域运动矢量最优概率分布.这两类特征中,第二类特征相对更加有效一些.而AoSO是现在运动矢量隐写分析公认最为有效的特征.
目前随着隐写算法更多注重运动矢量局部最优特性的保持,这在一定程度削弱了包括AoSO特征在内的最优性特征.此外,在现实环境中,视频尺寸往往较大,单个宏块的纹理较为平坦,利用运动矢量最优性特征进行检测较困难.因此,利用相关性进行运动矢量隐写分析则可能带来更好的检测效果.本文利用运动矢量的信息熵捕捉运动矢量相关性异常,克服了AoSO等隐写分析算法依赖局部最优原理的限制,提升了隐写分析特征的异常捕捉能力.
1 运动矢量与熵 1.1 最优性与相关性原理运动矢量最优性:如图 1所示,通过对任何一个原始运动矢量(H, V)加减1就可以得到其8个相邻的运动矢量.原始运动矢量(H, V)残差代价一般最小,因此也小于相邻的8个运动矢量代价[12],本文称这样的局部最低代价特性为运动矢量最优性.

|
| 图 1 (H, V)与8个相邻运动矢量位置关系 Figure 1 Location relationship among (H, V) and 8 local adjacent motion vectors |
运动矢量的隐写操作需要对运动矢量进行改写,文献[12]证明了这会导致残差能量变大,使得运动矢量这种局部最优特性被破坏,最优概率降低.
运动矢量相关性:视频宏块的运动矢量一般代表了该宏块内容在视频帧中的运动状态.相邻宏块在内容上一般属于同一整体,运动方式较为一致.因此,本文认为运动矢量的这种相似性为相关性.
如图 2所示,在正常的cover视频(左边)中,相邻宏块的运动矢量一般具有较好的一致性.当运动矢量被隐写过后,运动矢量在水平分量、垂直分量、方向以及长度上排列相对更加混乱,运动矢量的相关性一定程度上被破坏.

|
| 图 2 运动矢量的隐写使混乱度增大 Figure 2 Randomness of motion vectors are increased by steganography |
假设Λ和Δ为互相独立的二值信源,且Λ熵值小于Δ熵.现在将信源Λ产生的比特序列部分随机位置替换为Δ信源产生的比特.得到的新比特序列由两种信源比特交错排列而成,也可以看成两种信源的各自独立生成的比特序列相连接(这两种序列0和1的概率不变).由于Δ相比于Λ信源产生的0和1概率更接近,故熵值增大,即:
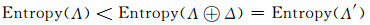
|
(1) |
其中,Entropy(Λ)<Entropy(Δ),Λ′是合并后的信源,Entropy(·)为熵值计算函数.
运动矢量的隐写就是在原始信源Λ的二进制信号序列中添加了秘密信息信源Δ的信号.为了提高隐写算法的嵌入效率,秘密信息信号Δ需要携带大量信息,熵值达到最大值1.而载体信号Λ受到相关性的影响,熵值处于相对较低水平.基于以上理论分析可知,在视频运动矢量隐写后,运动矢量信源熵值将增大.
1.3 最大理论熵值假设B为一个二值随机变量,产生0和1的概率分别为P0和P1.我们对B观测n次可以得到n个比特,并称这n个比特的观测为一轮观测.对于这一轮(n次)观测,本文用P(a, n-a)表示这n个比特中a个为0,n-a个为1的概率,那么P(a, n-a)服从二项分布:
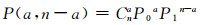
|
(2) |
根据熵计算公式,这一轮观测所得的n个比特的熵值期望计算如下:
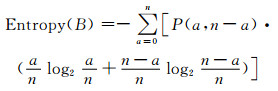
|
(3) |
这里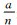
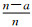
显然当P0=P1=0.5时,即前后两个比特不存在相关性,一轮观测熵值期望最大,公式(2) 和公式(3) 联立:
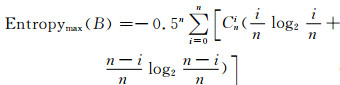
|
(4) |
这里Entropymax(B)表示随机二值变量B观测的最大熵值期望.显然当P0=P1=0.5时,一轮观测的熵值期望最大,仅与一轮观测的比特数n有关.
如图 3所示,横坐标为其观测数n,纵坐标为其观测最大熵的期望.进一步分析可知,当n趋近无穷大时,可观测统计出P0=P1=0.5,此时观测出的随机比特信号的熵为1.

|
| 图 3 观测次数及其最大熵值期望 Figure 3 Number of observations and expectation of maximum entropy |
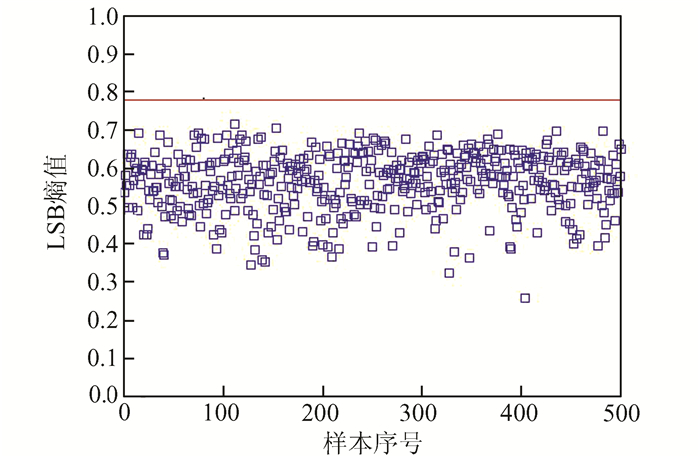
本文从30段cover视频中随机抽取500个P帧,计算各帧运动矢量H分量LSB位熵值期望(取n=4),计算结果如图 4所示.在cover样本中,H分量LSB位的熵(方块样本点)全部小于理论上限0.78.根据本文1.2部分的讨论,这表明在观测长度n=4情况下,P0和P1并不相同,即存在相关性.若运动矢量H分量的LSB位被改写后,P0和P1相比之前趋于相同,熵值会更靠近理论最大值0.78,即图 4中的横线.
|
| 图 4 cover样本H分量LSB位的熵在n=4时的分布及其上限 Figure 4 Distribution and upper limit of H component entropy of cover samples when n=4 |
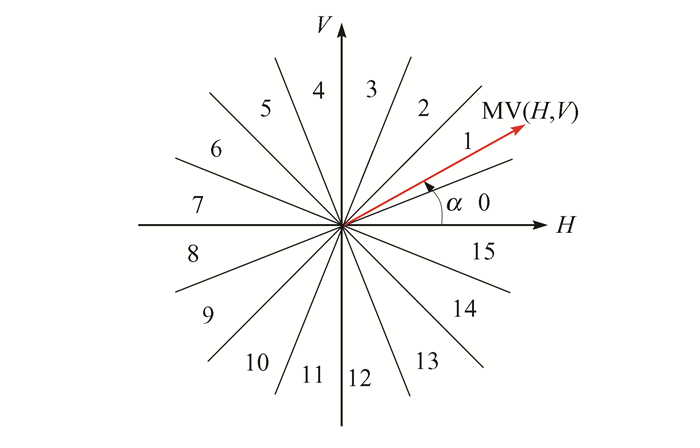
定义1 运动矢量(H, V)方向角α.如图 5所示,α为运动矢量MV与水平向右方向形成的角度,显然α∈[0, 2π).
|
| 图 5 运动矢量方向角及其量化数值 Figure 5 Motion vector direction angle and quantized value |
运动矢量的(H, V)方向角α可以通过下式进行计算:

|
(5) |
定义2 运动矢量方向角α量化值D.如图 5所示,运动矢量的方向角α可以分为16个区间,即量化为0~15共16个数值,故定义α量化值为D,
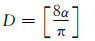
|
(6) |
其中[·]为截断取整(忽略小数部分),下同.
定义3 运动矢量的量化长度L, 即运动矢量的模长截断取整数值:
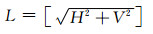
|
(7) |
定义4 量化函数q(Z, t)
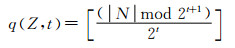
|
(8) |
量化函数q(Z, t)用于计算数值Z绝对值最低的第t位比特.
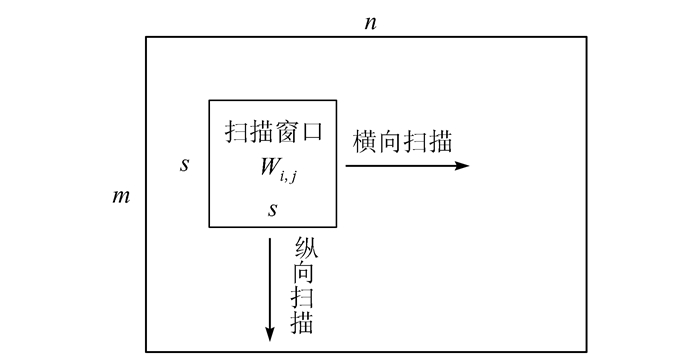
2.2 HVDL特征构造本文使用运动矢量的水平分量H、垂直分量V、量化的方向D和长度L构造16维的HVDL特征,其中每个分量最低4个比特分别构造4维特征,本文称基于该HVDL特征的隐写分析方法为HVDL方法.对于每一m行和n列的inter宏块(16×16像素大小)排列构成的视频帧,定义一个长和宽都为s个inter宏块(s<m且s<n,本文取s=3) 的滑动窗口,记为Wi, j(i=0, 1, 2, …, m-s-1且j=0, 1, 2, …, n-s-1,).如图 6所示,Wi, j共定义了(m-s)(n-s)个子窗口:
|
| 图 6 扫描运动矢量的子窗口 Figure 6 Sub windows for motion vector scanning |
子窗口Wi, j内运动矢量个数记为Ki, j,其中第k个运动矢量记为(hki, j, vki, j),对应的方向角量化值为dki, j,量化长度为lki, j,4×4大小的量化矩阵为Qki, j=(qkx, y)4×4,x, y=0, 1, 2, 3.统计滑动窗口内Ki, j个矩阵Qki, j每个元素0或1概率后,计算得到4×4熵均值矩阵Entx, y,x, y=0, 1, 2, 3.算法描述如下.
| 算法 扫描窗口熵均值计算 |
| 输入:m×n视频帧,子窗口大小s |
| 输出:熵均值Entx, y,x, y=0, 1, 2, 3 |
| 1. for i=0 to m-s do: |
| 2. for j=0 to n-s do: |
| 3. 获取子窗口Wi, j内共Ki, j个运动矢量集合:Vi, j={MVki, j=(hki, j, vki, j)|0≤k<Ki, j} |
| 4. for k=0 to Ki, j-1 do: |
5. 计算Wi, j中第k个运动矢量方向角量化值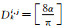 |
6. 计算Wi, j中第k个运动矢量长度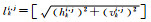 |
7. 计算Qki, j=(qkx, y)4×4=  , x, y=0, 1, 2, 3 , x, y=0, 1, 2, 3 |
| 8. end for |
9. 计算 |
| 10. 计算Ei, j={ex, yi, j=-(px, yi, jlog2(px, yi, j)+(1-px, yi, j)log2(1-px, yi, j))|x, y=0, 1, 2, 3} |
| 11. end for |
| 12. end for |
13.返回4×4熵均值矩阵:Entx, y= 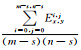 ,x, y=0, 1, 2, 3 ,x, y=0, 1, 2, 3 |
该算法首先使用大小为3×3(即s=3) 窗口进行扫描.窗口内的所有运动矢量都被计算HVDL 4个分量.然后,统计窗口内各个分量最低4个比特的0和1概率,计算比特的熵,这样可以计算出4×4的熵值矩阵.最后,移动窗口可以得到多个熵值矩阵,求矩阵中每个元素的均值即可得到并返回4×4大小的熵均值矩阵Entx, y.
我们将4×4大小的均值矩阵Entx, y将转换为一个16维向量,得到HVDL特征,即:
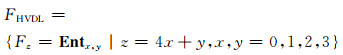
|
本实验采用50段分辨率为1 920×1 080像素的DV拍摄视频,先裁剪后缩放成分辨率为800×600像素的MPEG-4格式,比特率为2 500 Kb/s,全部采用16×16像素inter块.嵌入强度为0.2,0.4和0.6 bpmv(bpmv,即bit per motion vector,表示平均每个运动矢量嵌入的比特数).随机挑选25段cover及其对应stego视频,每段视频提取100帧用于训练,即共2 500 cover帧和2 500 stego帧作为训练帧.剩余25段视频作为测试视频,每段提取100帧用于测试,即共2 500 cover帧和2 500 stego帧作为预测帧.
3.2 熵区分度测试为了进行特征区分能力测试,本文利用cover样本和stego样本进行特征对比.其中stego样本为相对嵌入率为0.8 bpmv的Xu算法[3]隐写样本.
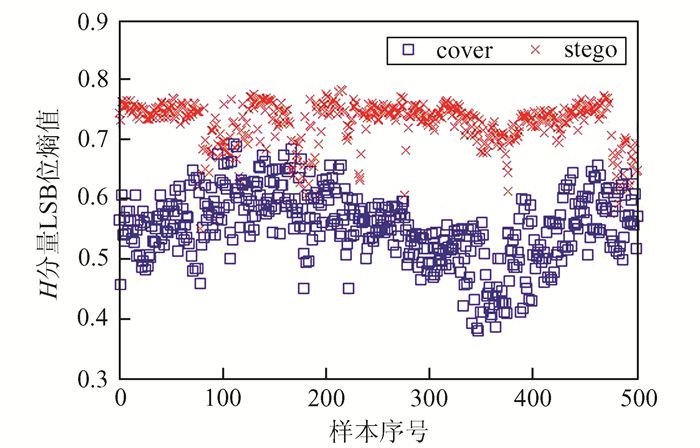
图 7为单个视频内,取n=4,计算连续的500个P帧运动矢量H分量LSB位的熵值,比较嵌入前后变化.原始cover样本的熵数值处于较低水平,隐写过后熵值显著增大逼近理论上限0.78.
|
| 图 7 cover与stego样本H分量LSB位熵值 Figure 7 H component LSB entropy of cover and stego samples |
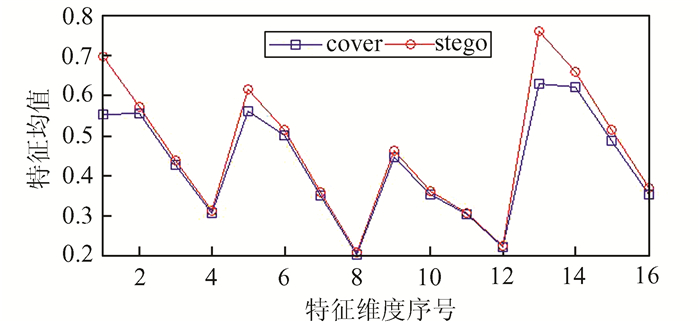
进一步地,本文从30个cover视频样本(共3 000个cover帧)和30个stego视频样本(共3 000个stego帧),分别提取每一帧的16维HVDL特征,cover和stego帧分别取均值对比,结果如图 8所示.其中,横坐标为HVDL特征(共16维)中每个维度的序号,即1~16,纵坐标为特征序号所对应特征的均值.可以看出,stego样本的HVDL特征均值相比cover样本较大,这表明隐写造成了特征均值的增加,本文的HVDL各个维度特征对于隐写有区分作用.
|
| 图 8 cover与stego样本16维HVDL特征均值对比 Figure 8 Comparison of the mean value of 16-dimension HVDL feature between cover and stego samples |
将本文算法与AoSO比较,对Xu[3], Aly[4],Cao[5]和MVMPLO[8]每种隐写算法对应的2 500个cover帧与2 500个stego帧样本进行测试,检测准确率(使用百分比表示)如表 1所示.其中,分类器采用lib-svm,并使用多项式核函数训练.
| % | ||||
| 检测特征 | 隐写算法 | 0.2 bpmv | 0.4 bpmv | 0.6 bpmv |
| AoSO | Xu | 74.92 | 87.38 | 92.18 |
| Aly | 73.00 | 80.86 | 87.62 | |
| Cao | 54.62 | 63.00 | 68.30 | |
| MVMPLO | 49.58 | 51.00 | 54.96 | |
| HVDL | Xu | 67.02 | 84.02 | 89.66 |
| Aly | 62.00 | 69.36 | 76.42 | |
| Cao | 59.98 | 71.98 | 79.12 | |
| MVMPLO | 63.78 | 66.74 | 71.72 | |
| 注:AoSO和HVDL的比较,黑体表示效果更好. | ||||
实验结果表明,早期的Xu和Aly算法对于安全性考虑不够充分,AoSO和HVDL都可进行有效检测,而前者效果较好一些.但近年来新隐写算法更加注重保持运动矢量的局部最优性,这使得算法的安全性有了较大提升.本实验中的Cao和MVMPLO方法通过编码控制运动矢量的隐写失真代价让AoSO检测准确率始终处于较低水平.本文HVDL特征由运动矢量信息熵构造,发挥了不依赖运动矢量局部最优性来捕捉隐写异常的优势,因此和AoSO相比有相对更高的检测率.特别是针对基于STC编码的MVMPLO算法,HVDL检测准确率提升效果显著.
3.4 特征计算时间比较测试样本:选取25段视频,每段前100帧提取特征.
硬件条件:I5-3470 3.20Hz四核处理器,4GB DDR3内存,32位Win7系统.分别提取AoSO和HVDL特征,提取特征所用时间如表 2所示.
| 比较特征 | 总时间/s | 每帧时间/ms |
| AoSO | 247.1 | 82.4 |
| HVDL | 56.2 | 18.7 |
提取AoSO特征需要结合残差进行运动矢量特征提取,计算过程复杂度相对较高.本文HVDL运动矢量特征具有更低的维度,且运算基于运动矢量相关性,无需残差代价计算,特征算法的运算速度相比于AoSO有提高.
4 结论随着数字视频媒体的普及以及新隐写算法的出现:一方面,大尺寸视频更加常见,而其单个宏块纹理相对平坦,隐写算法对运动矢量局部最优特性破坏较小;另一方面,新隐写算法越来越注重做到局部最优性的保持.这两点导致AoSO等隐写分析特征的检测能力被削弱.本文利用运动矢量相关性及其被隐写后混乱程度增加的原理,提出一种新的HVDL熵特征.该特征描述运动矢量的水平分量、垂直分量、矢量方向以及矢量长度最低4个比特的混乱程度.实验表明,cover视频的运动矢量具有较高的一致性,各熵值处于较低的状态,当运动矢量隐写后,熵值增加显著.通过与AoSO特征的对比发现,本文算法与Cao和MVMPLO两种安全性较高的隐写算法相比有更好的检测效果.特征的提取不必进行残差代价计算,相比AoSO有更快的计算速度.该特征利用了运动矢量的4个变量进行特征构造,后期可挖掘运动矢量更多熵变量构造更高维度特征,可进一步提升检测准确率.此外,基于本文讨论的熵增加原理,可以在文本、图像、音频等载体上设计类似隐写分析特征.
| [1] |
LI B, HE J H, HUANG J W, et al. A survey on image steganography and steganalysis[J]. Journal of Information Hiding and Multimedia Signal Processing, 2011, 2(2): 142-172. |
| [2] |
TEW Y, WONG K S. An overview of information hiding in H. 264/AVC compressed video[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2014, 24(2): 305-319. DOI:10.1109/TCSVT.2013.2276710 |
| [3] |
XU C Y, PING X J, ZHANG T. Steganography in Compressed Video Stream[DB/OL].[2016-08-09]. http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=1691792. DOI:10.1109/ICICIC.2006.158.
|
| [4] |
ALY H A. Data hiding in motion vectors of compressed video based on their associated prediction error[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(1): 14-18. DOI:10.1109/TIFS.2010.2090520 |
| [5] |
CAO Y, ZHAO X F, FENG D G, et al. Video steganography with perturbed motion estimation[C]//Information Hiding. Berlin:Springer-Verlag, 2011:193-207. DOI:10.1007/978-3-642-24178-9_14.
|
| [6] |
FILLER T, JUDAS J, FRIDRICH J. Minimizing additive distortion in steganography using syndrome-trellis codes[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(3): 920-935. DOI:10.1109/TIFS.2011.2134094 |
| [7] |
CAO Y, ZHANG H, ZHAO X F, et al. Video steganography based on optimized motion estimation perturbation[C]//Proceedings of the 3rd ACM Workshop on Information Hiding and Multimedia Security.New York:ACM, 2015:25-31. DOI:10.1145/2756601.2756609.
|
| [8] |
ZHANG H, CAO Y, ZHAO X F. Motion vector-based video steganography with preserved local optimality[J]. Multimedia Tools and Applications, 2016, 75(21): 13503-13519. DOI:10.1007/s11042-015-2743-x |
| [9] |
YAO Y Z, ZHANG W M, YU N H, et al. Defining embedding distortion for motion vector-based video steganography[J]. Multimedia Tools and Applications, 2015, 74(24): 11163-11186. DOI:10.1007/s11042-014-2223-8 |
| [10] |
SU Y T, ZHANG C Q, ZHANG C T. A video steganalytic algorithm against motion-vector-based steganography[J]. Signal Processing, 2011, 91(8): 1901-1909. DOI:10.1016/j.sigpro.2011.02.012 |
| [11] |
CAO Y, ZHAO X F, FENG D G. Video steganalysis exploiting motion vector reversion-based features[J]. Signal Processing Letters, 2012, 19(1): 35-38. DOI:10.1109/LSP.2011.2176116 |
| [12] |
WANG K R, ZHAO H, WANG H X. Video steganalysis against motion vector-based steganography by adding or subtracting one motion vector value[J]. IEEE Transactions on Information Forensics and Security, 2014, 9(5): 741-751. DOI:10.1109/TIFS.2014.2308633 |
 2017, Vol. 63
2017, Vol. 63




