0 引言

若P ∈ ^n×n且满足P²= P, 则称P是上的幂等矩阵或者投射子.幂等矩阵是一类重要且性质非常丰富的矩阵，在线性算子理论、统计学、几何学、控制理论中有重要应用^[1~4].近年来, 中外学者对各种特殊矩阵的组合的相关性质进行了广泛和深入地研究.文献[5]证明了复数域上两个非零的幂等矩阵P, Q线性组合aP +bQ (a, b, a+b≠0)的可逆性与系数的选取无关.文献[6]进一步得到了aP +bQ (a, b, a+b≠0)的秩与系数的选取无关.随后, 研究人员发现对于Hilbert空间上的有界幂等线性算子P, Q, aP +bQ (a, b, a+b≠0)的值域, 可逆性, Fredholm性等也有类似的上述性质^[7~10].这些研究工作启发了人们对各种特殊矩阵及算子线性组合的性质与其系数关系的深入探讨^{[11, 12]}. 2009年, 文献[13, 14]分别考虑了幂等矩阵P, Q的组合

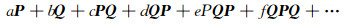
与

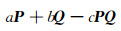
的可逆性与系数的关系，推广了前人的结果.随后, 对上述组合的各种广义逆的存在性、广义逆的表达式与系数的关系引起了热烈的讨论^[15~20]. 2011年, 文献[21]证明了若P, Q是复数域上的两个不同的非零幂等矩阵, 且满足(QP)²=0, 则组合

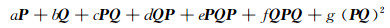
(1)

的群逆存在, 其中a, b≠0.另外, 文献[21]还得到了组合(1)的群逆表达式.

在上述研究的基础上，一个问题自然地被提出来，即若 P, Q是复数域上的两个不同的非零幂等矩阵, 且满足(QP)ⁿ=0或(PQ)ⁿ=0(n≥2), 则组合

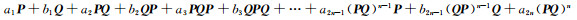
(2)

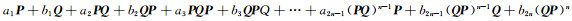
(3)

的群逆是否存在, 其中a₁, b₁≠0？若组合(2)和(3)群逆存在, 其群逆表达式是怎样的？

本文运用矩阵零空间的性质证明了复数域上两个非零的幂等矩阵P, Q的组合(2)和(3)分别在条件(QP)ⁿ=0, (PQ)ⁿ=0(n≥2)下的秩与系数的选取无关，并进而证明了其群逆存在.另外，还得到了组合aP +b Q +cPQ +dQP在条件(QP)ⁿ=0或(PQ)ⁿ=0下的群逆表达式.本文证明组合(2)的群逆存在性的方法与文献[21]不同.

1 预备知识

设^n×n是复数域上所有n阶矩阵构成的集合, 对于A ∈ ^n×n, 若存在X ∈ ^n×n使得

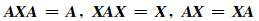
成立，则称X为A的一个群逆.若A存在群逆, 则其群逆唯一, 记A的群逆为A_g.对于A ∈ ^n×n, A_g存在当且仅当r(A²)=r(A), 其中r(A)表示A的秩.

引理1^[21]  设P, Q是^n×n上的两个不同的非零幂等矩阵, 且满足(QP)²=0, 则对任意的a, b, c, d, e, f, g∈ , 其中a, b≠0, 组合

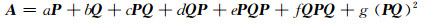
的群逆存在, 且

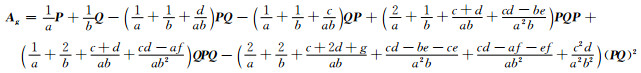
容易举例说明(PQ)²=0并不意味着(QP)²=0, 反之也成立.

引理2^[21]  设P, Q是^n×n上的两个不同的非零幂等矩阵, 且满足(PQ)²=0, 则对任意的a, b, c, d, e, f, h∈ , 其中a, b≠0, 组合

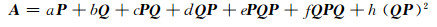
的群逆存在, 且

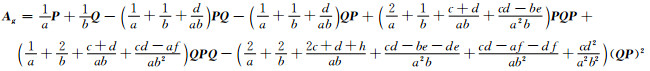
例1  令

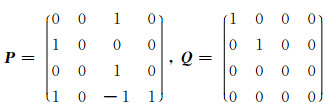
则可得到P, Q是幂等矩阵, 且满足(QP)²≠0, (QP)³=0.另外, 若P, Q满足(QP)²=0, 则(QP)³=(QP)² QP =0.因此条件(QP)³=0比条件(QP)²=0弱.条件(PQ)ⁿ=0比条件(PQ)^n－1=0 (n≥2)弱.另外, 条件(PQ)ⁿ=0与(QP)ⁿ=0之间也没有蕴含关系.所以在条件(QP)ⁿ=0或(PQ)ⁿ=0下讨论组合(2)和(3)群逆的存在性及表达式是有意义的.

2 主要结论

下面将证明复数域上两个非零幂等矩阵P, Q的组合(2)和(3)分别在条件(QP)ⁿ=0, (PQ)ⁿ=0(n≥2)下的秩与系数的关系，进而讨论其群逆的存在性.

定理1  设P, Q是^n×n上的两个不同的非零幂等矩阵, Φ为(2)式，其中a_i, b_j∈ (1≤i≤2n, 1≤j≤2n－1)且a₁b₁≠0.若(QP)ⁿ=0, 则以下结论成立:

1) N(Φ)=N(P)∩N (Q)；

2) r(Φ)是一个常数且r(Φ) =r (P + Q), 从而Φ可逆当且仅当P + Q可逆；

3) Φ存在群逆.

其中N(A)表示矩阵A的核空间, 即N(A) = {x ⁿ|Ax =0}.

证   1)一方面, 设∀α∈N(P)∩N(Q), 则有Pα= Qα=0, 所以Φα=0, 因此

N(P)∩N(Q) ⊆N(Φ).另一方面, 设⊆α∈N(Φ), 则

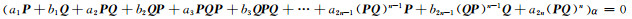
(4)

在(4)式两边左乘(QP)^n－1Q, 并注意到(QP)ⁿ=0可得b₁(QP)^n－1Qα=0.

因为b₁≠0, 所以

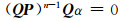
(5)

在(4)式两边右乘(PQ)ⁿ, 并注意到(QP)ⁿ=0可得a₁(PQ)ⁿα=0.

因为a₁≠0, 所以

(6)

在(4)式两边左乘(QP)^n－1, 并注意(5)式，则b₁(QP)^n－1α=0, 可得(QP)^n－1α=0.依次在(4)式两边左乘(QP)^n－2Q, (QP)^n－2, (QP)^n－3Q, (QP)^n－3, …, QP, Q, 可得

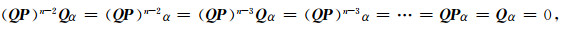
同理依次在(4)式两边左乘

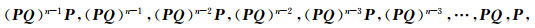
可得

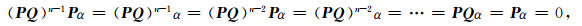
从而α∈N(P)∩N(Q).所以N(Φ)⊆N(P)∩N(Q).因此N(Φ) =N(P)∩N(Q).

即结论1)成立.

2) 因为r(Φ) =n－dim(N (Φ)) =n－dim(N (P)∩N (Q))是一个常数, 所以r (Φ)与满足条件a₁, b₁≠0的系数a_i, b_j∈ (1≤i≤2n, 1≤j≤2n－1)选取无关.特别地, 取a₁=b₁=1, a_i=b_j=0(1≤i≤2n, 1≤j≤2n－1), 则r (Φ) =r (P +Q).从而r(Φ)可逆当且仅当P + Q可逆.

3) 注意到

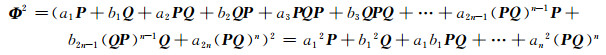
且Φ²的系数a₁²≠0, b₁²≠0, 即Φ²的系数满足定理的条件, 由结论1)和2)知

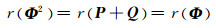
从而Φ的群逆存在.

定理2  设P, Q是^n×n上的两个不同的非零幂等矩阵, Φ为(3)式，其中a_i, b_j∈ (1≤i≤2n, 1≤j≤2n－1)且a₁b₁≠0.若(PQ)ⁿ=0, 则以下结论成立:

1) N(Φ) =N (P)∩N (Q)；

2) r(Φ)是一个常数且r(Φ) =r(P + Q), 从而Φ可逆当且仅当P + Q可逆；

3) Φ存在群逆.

证  类似定理1的证明.

下面考虑组合aP +bQ +cPQ +dQP在条件(QP)ⁿ或(PQ)ⁿ下的群逆公式.

定理3  设a, b, c, d∈ , 且满足a≠0, b≠0, A =aP +bQ +cPQ +dQP, 其中P, Q是^n×n上两个不同的非零幂等矩阵，且满足(QP)ⁿ=0, 则A存在群逆, 且表达式为

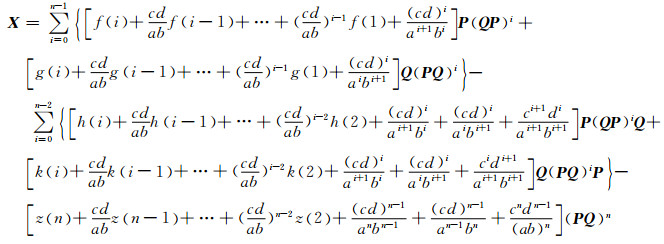
其中,

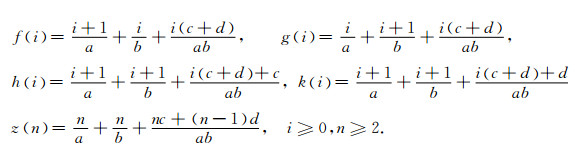
证  令X = X₁+ X₂+ X₃, 其中,

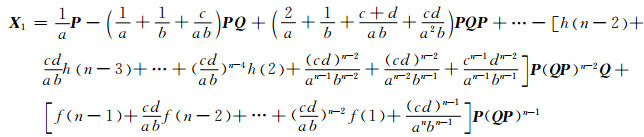
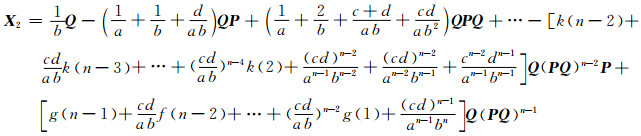
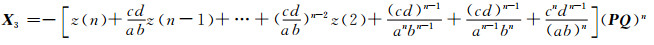
由(QP)ⁿ=0可知,

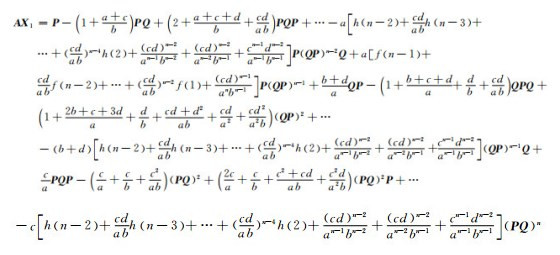
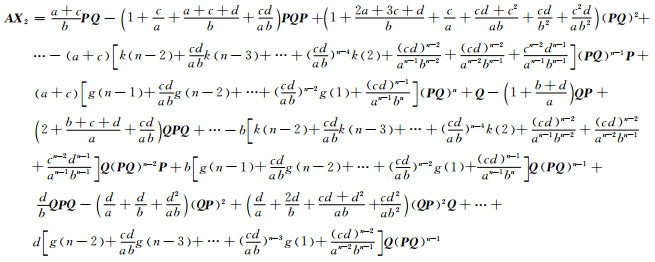
所以

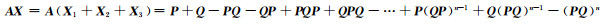
又因为

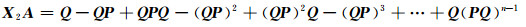
所以,

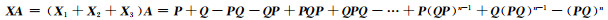
因此AX = XA.

又因为

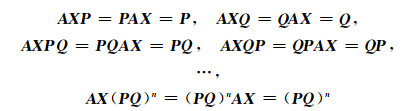
所以AXA = A, XAX = X.

故由群逆的惟一性知，X为A的群逆.

定理4  设a, b, c, d∈ , 且满足a≠0, b≠0, A =aP +bQ +cPQ +dQP, 其中P, Q是^n×n上两个不同的非零幂等矩阵，且满足(PQ)ⁿ=0, 则A存在群逆, 且表达式为

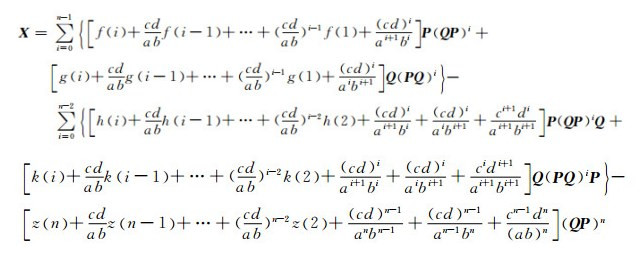
其中,

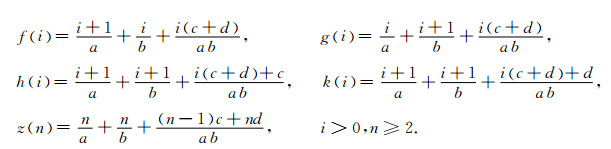
证  类似定理3的证明.

3 结论

本文讨论了复数域上两个不同的非零幂等矩阵P, Q的组合

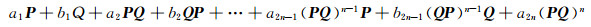
(其中a₁, b₁, …, b_2n－1, a_2n∈ , a₁, b₁≠0)在条件(QP)ⁿ=0(n≥2)下的秩与系数的关系及其群逆的存在性，还研究了组合aP +b Q +cPQ +dQP在条件(QP)ⁿ=0下的群逆的计算公式.研究上述组合在其他条件下的广义逆的存在性及表达式是一个可以继续讨论的问题.