文章信息
- 刘文瑞 , 易世界 , 栗娟 , 杨威 , 刘进 . 2016
- LIU Wenrui, YI Shijie, LI Juan, YANG Wei, LIU Jin . 2016
- 基于贝叶斯服务依赖图的错误定位
- Bayesian Service Dependence Graph for Fault Location
- 武汉大学学报(理学版), 2016, 62(3): 268-274
- Journal of Wuhan University(Natural Science Edition), 2016, 62(3): 268-274
- http://dx.doi.org/10.14188/j.1671-8836.2016.03.010
-
文章历史
- 收稿日期:2015-03-02

服务计算是软件开发的一种新的分布式计算范型.近年来,以复合服务的方式实现业务逻辑复杂的任务成为了一种新的趋势.复合服务的软件开发中,个体服务的失效可能导致整个复合服务失效.复合服务在执行过程中,个体服务失效的原因可能有:网络通信异常,服务基础设施失效等导致服务无法正常调用;服务接口及QoS值的动态变化导致个体服务间无法正常交互,交互结果错误;QoS违反属性约定的SLA协议等[1~3].因此为了提高复合服务的质量,找到错误服务是一项重要任务.
尽管错误服务的定位已引起了学者们的广泛兴趣[4, 5],但是已有的研究多采用基于一致性的诊断.这种方法对于错误定位过程中的输入、服务执行以及输出之间存在的不确定性不能进行处理.实际上,复合服务执行过程中,个体服务之间的业务数据交互和业务逻辑依赖导致个体服务的错误会在复合服务执行过程中传播和积累,并导致个体服务间的错误具有因果关系,这种因果关系不一定是确定的.同时,在复合服务环境中,收集到的异常数据往往不完整,这些不确定性极大地增加了错误服务定位的难度.
因此,本文提出一个基于贝叶斯服务依赖图的错误定位方法.贝叶斯服务依赖图兼具服务依赖图和贝叶斯网络的特征,既有效地描述了服务之间的依赖关系,又用为其隐含的错误因果关系推理提供了强有效的理论模型.因此,基于贝叶斯服务依赖图,采用贝叶斯网络推理的方法可以对错误服务进行定位.
本文主要贡献在于:
1) 挖掘个体服务间的控制依赖关系,有效地描述了服务间的业务逻辑依赖.
2) 提出了贝叶斯服务依赖图模型,该模型兼具服务依赖图和贝叶斯网络的特征,既有效地描述了服务之间的依赖关系,又用贝叶斯网络为其因果关系推理提供了强有效的理论模型.
1 复合服务执行流程的建模及转换本节针对复合服务执行流程中的4种结构:串行结构,并行结构,选择结构和循环结构详细介绍复合服务执行流程转换为贝叶斯服务依赖图的过程.
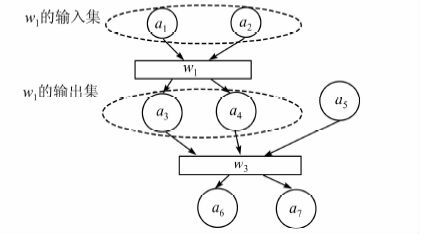
1.1 服务依赖图服务依赖图是由属性节点(服务输入/输出)及操作节点(服务)组成的图,用来描述不同服务间所有可能的输入/输出依赖.服务依赖图中,服务被描述为一个具有输入集和输出集的操作节点[6, 7].图1所示是一个服务依赖图实例.
|
| 图 1 服务依赖图 Figure 1 Service dependence graph |
实际上,服务依赖图描述的是个体服务间的数据交互,并不涉及业务流程中个体服务间的逻辑依赖.复合服务执行流程向贝叶斯服务依赖图转换过程中,既要考虑这种个体服务间的数据交互,也要考虑服务间的逻辑依赖.
1.2 贝叶斯网络模型贝叶斯网络是目前用于不确定知识表达和推理领域最有效的理论模型之一.它是一个表示随机变量间依赖和独立关系的网络模型.贝叶斯网络是有向无环图形结构,其中节点代表问题域的随机变量,节点间的有向边代表变量间的直接依赖关系[8~10].基于贝叶斯网络的故障诊断主要是应用贝叶斯网络的逆向推理功能,即已知结果节点,推断各级父节点发生错误的概率.
1.3 复合服务执行流程中的两种依赖定义1(数据依赖):在复合服务执行流程中,若两个体服务之间存在业务数据交互,这种数据的交互定义为数据依赖.
定义2(控制依赖):在复合服务执行流程中,由于业务逻辑的关系,个体服务的执行必须有先后顺序,这是个体服务间业务逻辑的依赖,称之为控制依赖.
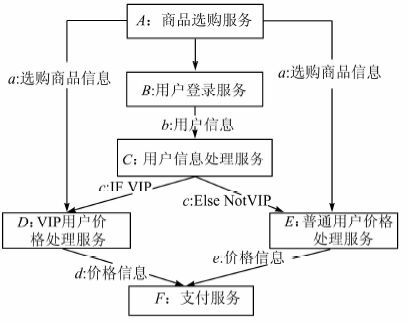
图1所示的服务依赖图中,服务w1输出数据a3,a4,以数据a3,a4作为输入的服务w3与w1二者存在数据依赖,记做w1$\xrightarrow{a}$w3,其中,w1称为w3的数据依赖服务.而控制依赖取决于4种流程结构.如图2所示的复合服务“购物服务”由服务序列[A,B,C,D,E,F]组成,购物开始时,执行商品购物服务,接着执行用户登陆服务,用户信息处理服务,若用户是VIP则执行VIP价格处理服务,否则执行非VIP价格处理服务,最后执行支付服务.在该服务复合中,由于服务A与服务B在业务逻辑上,必须是服务A执行完后服务B才可以执行,这种串行结构决定了服务B控制依赖于A,记做A→B,其中A称为B的控制依赖服务.
|
| 图 2 购物服务 Figure 2 Shopping service |
复合服务执行流程中的边表示个体服务间的业务逻辑或者数据交互.而贝叶斯网络中的边表示节点间的一种因果关系.因此需要挖掘复合服务执行流程中节点间隐含的因果关系.
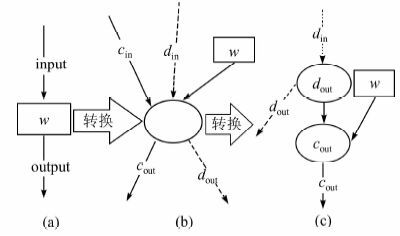
服务结果的执行正确与否取决于三个方面:数据输入din1,din2,…,dinn即本服务数据依赖服务的输出,控制输入cin1<in2,…,cinm即本服务控制依赖服务执行正确与否,和本服务的执行.也就是说,这三个方面是服务输出结果正确与否的原因.据此,将复合服务执行流程转换为贝叶斯服务依赖图的过程如图3(a)和(b)所示.为了区分控制流与数据流,将输出节点裂变为数据节点和控制节点,如图3(b)和(c)所示output节点裂变为数据节点dout和控制节点cout.
|
| 图 3 单个服务的转换图 Figure 3 Transformation of individual service |
Web服务组合由分布式的单个服务组合而成,有四种基本组合结构:串行结构,并行结构,选择结构,循环结构.根据个体服务的转换过程,将基本组合结构转换为相应的贝叶斯服务依赖图.
1) 串行结构
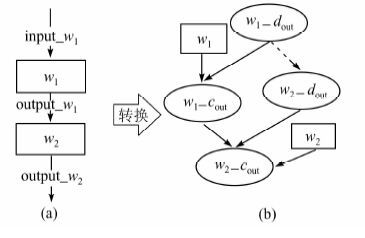
串行结构是指根据业务逻辑,依次执行单个服务,一个服务执行完成后才可执行下一个服务.如图4所示,串行结构4(a)表示服务w1,w2之间既有数据依赖也有控制依赖.其转换后的贝叶斯服务依赖图如图4(b)所示.
|
| 图 4 串行结构及其对应贝叶斯服务依赖图 Figure 4 Serial structure and corresponding Bayesian service dependence graph |
2) 选择结构
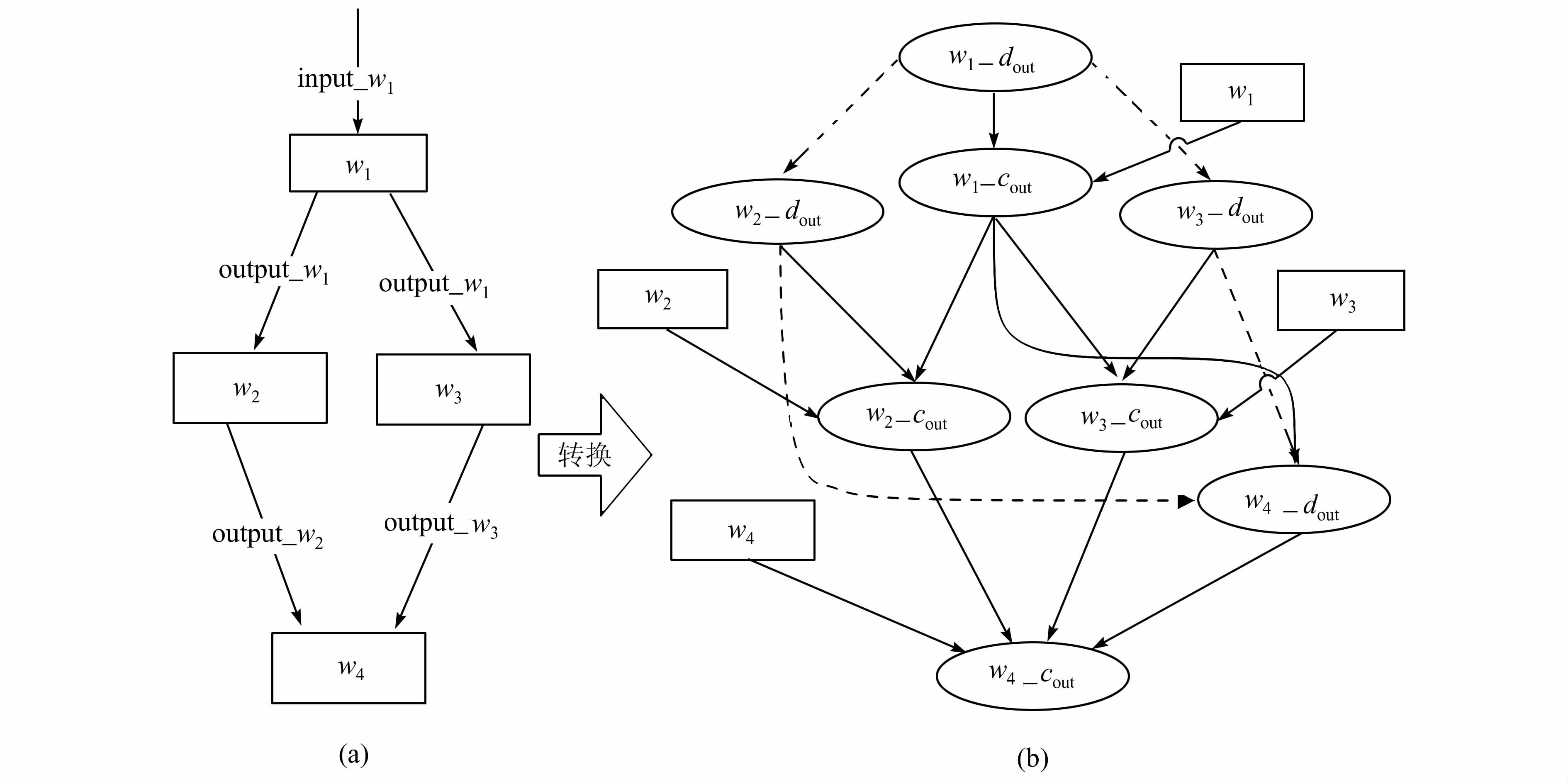
选择结构是指根据条件,选择Web服务分支执行.如图5(a)所示,转换后的贝叶斯服务依赖图如图5(b).选择结构中,选择分支的末端服务如图5(a)中服务w4,它既控制依赖于逻辑上它的上一个服务w2,同时又控制依赖于选择条件中的服务w1.
|
| 图 5 选择结构及其对应贝叶斯服务依赖图 Figure 5 Selective structure and corresponding Bayesian service dependence graph |
3) 并行结构
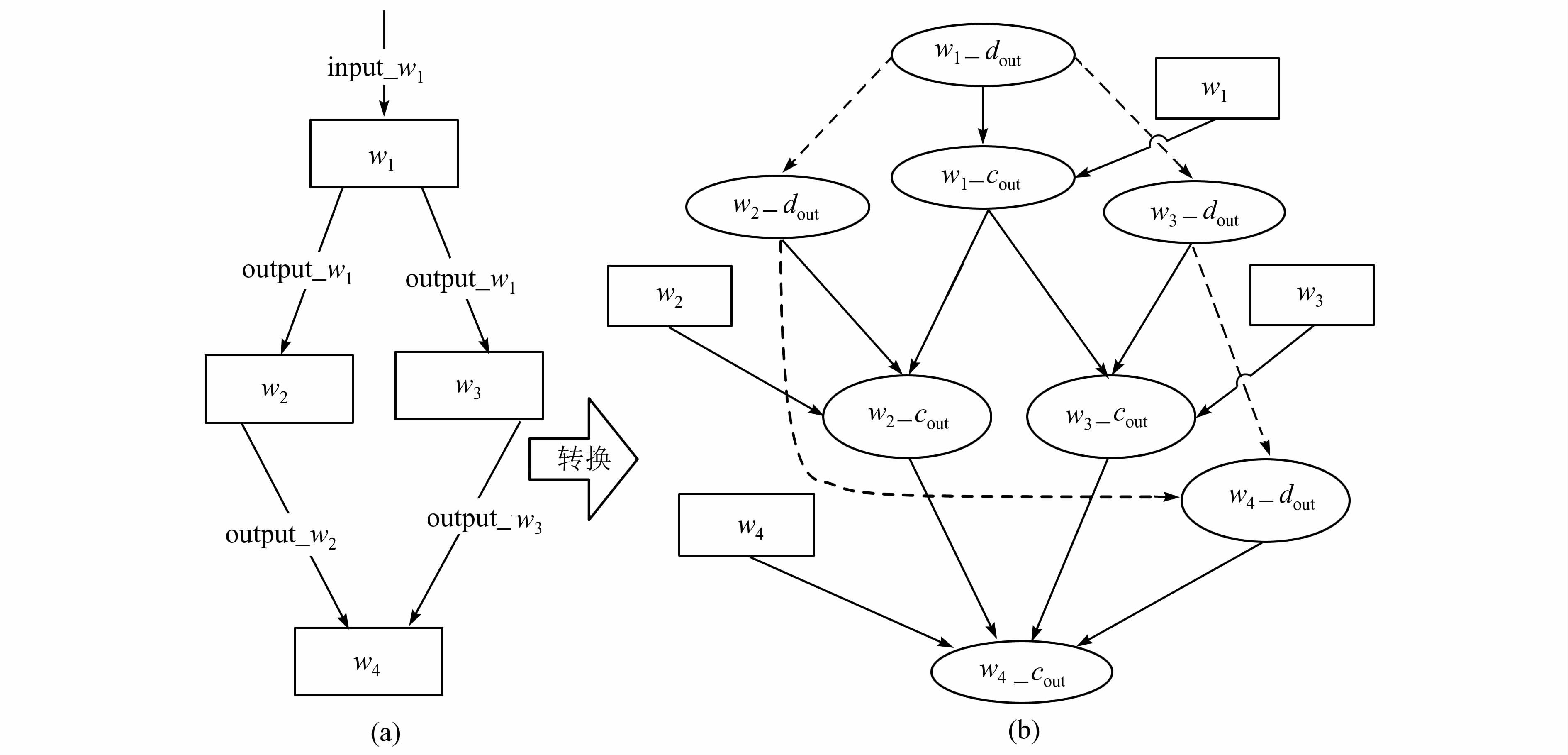
并行结构是指两种或者两种以上的服务并行执行的结构(图6(a)).转换后的贝叶斯服务依赖图如图6(b)所示.
|
| 图 6 并行结构及其对应贝叶斯服务依赖图 Figure 6 Parallel structure and corresponding Bayesian service dependence graph |
4) 循环结构
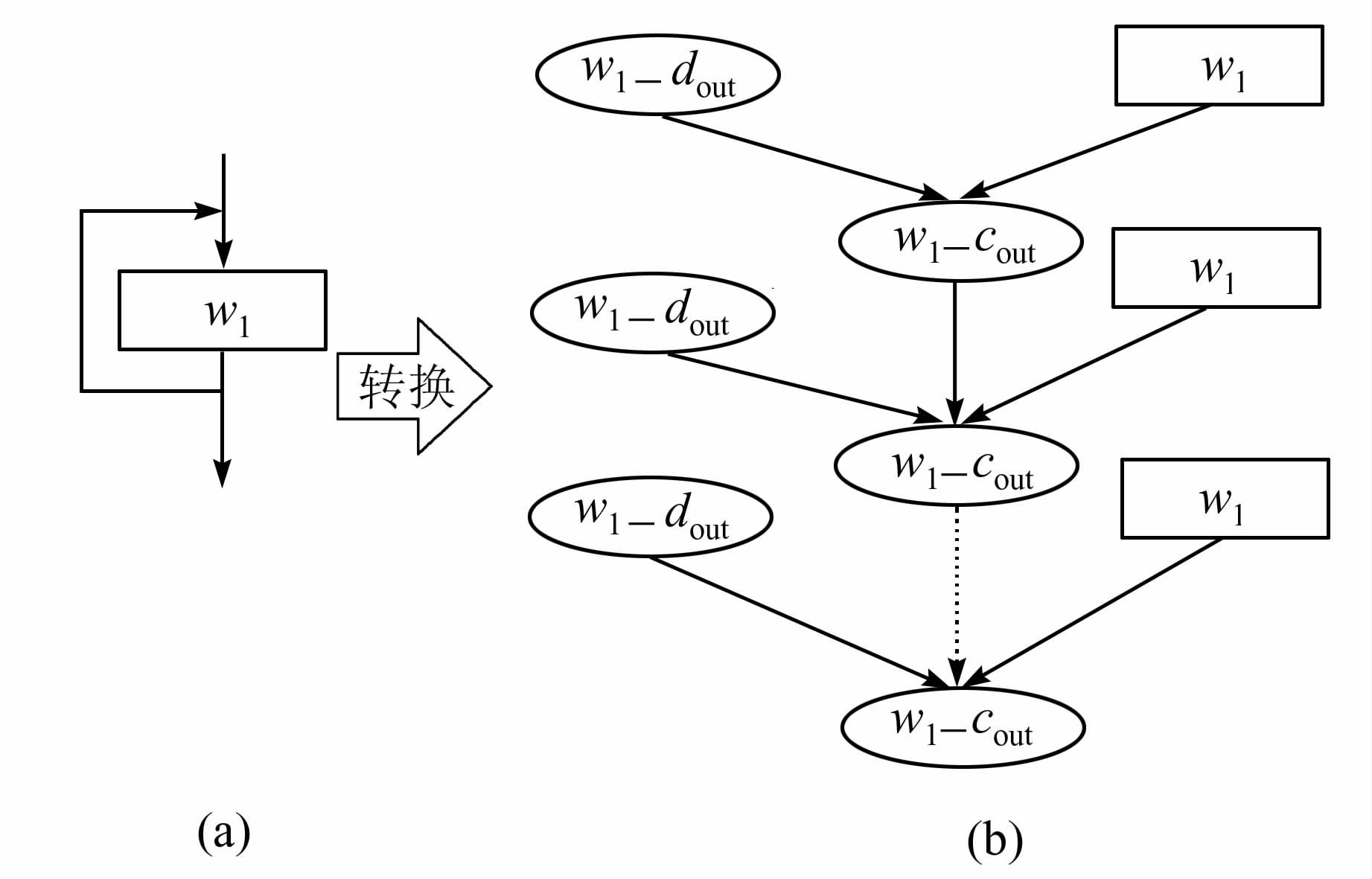
循环结构是指满足条件的前提下重复执行一个或者多个Web服务.由于贝叶斯网络是有向无环图,因此循环结构转换时,需将循环路径展开,转换方法类似顺序结构.如图7(a)所示的循环结构转换后的贝叶斯服务依赖图如图7(b)所示.
|
| 图 7 循环结构及其对应贝叶斯服务依赖图 Figure 7 Loop structure and corresponding Bayesian service dependence graph |
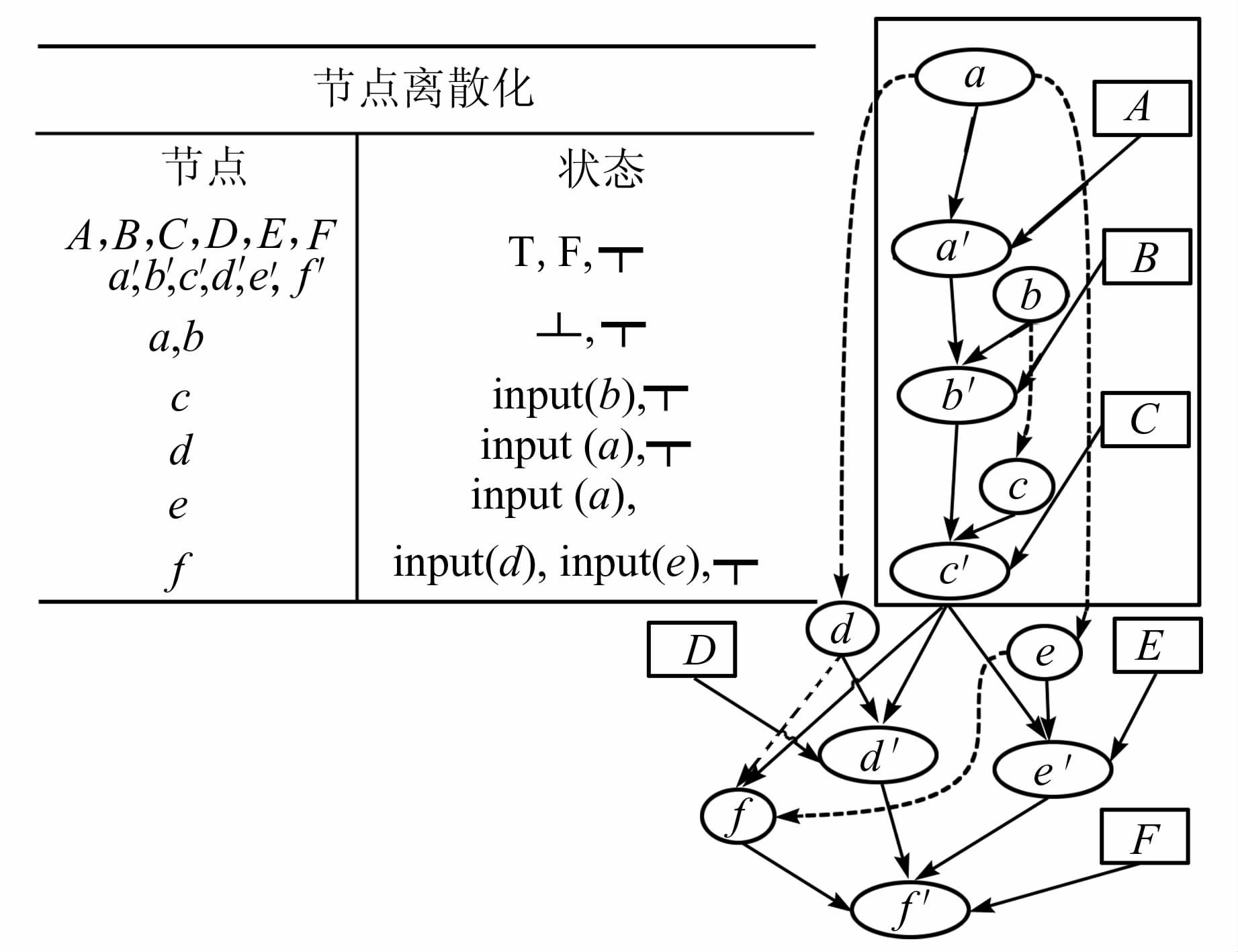
根据转换规则,图2所示的复合服务购物服务执行流程转换为贝叶斯服务依赖图如图8所示.图中,节点X表示服务节点,x表示数据节点,x′表示控制节点.
|
| 图 8 购物服务的贝叶斯服务依赖图 Figure 8 Bayesian Service Dependence Graph of shopping service |
贝叶斯网络推理需要确定每个非内部节点状态的先验概率及每个内部节点状态的条件概率.因此,要将贝叶斯服务依赖图中的每个节点的状态离散化.对于贝叶斯服务依赖图中的每个服务节点及控制节点,定义三种状态{T,F,┬},分别表示正确,错误和未执行.数据节点的状态由数据的来源决定,故图8中节点f的状态有三种,{input(d),input(e),┬},分别表示数据输入来源于d,或者e或者未执行.对于非内部的数据节点其状态有两种{┴,┬},分别表示执行状态和未执行状态.图8所示的贝叶斯服务依赖图中的节点离散化后,每个节点的状态如图8中表格所示.
3 参数学习使用贝叶斯网络进行逻辑推理,需要确定每个内部节点(有父节点的节点)的条件概率和非内部节点的先验概率.QoS从运行代价、执行时间、吞吐量、可靠性、荣誉度等多个方面反映Web服务的性能.其中,服务的可靠性反映了其可靠程度,可靠性越高则服务失效的频率越低[11, 12],因此对于每个服务节点w(图4(b)方框所示),本文将服务的可靠性作为其先验概率Prs,按下式计算,
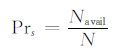
|
其中,Navail表示服务s调用的可用次数,N表示服务s调用的总次数.
对于非内部节点M,其某个状态值s的先验概率PrsM可根据历史运行数据进行统计学习.
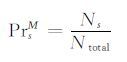
|
其中,Ns表示节点M状态s出现的次数,Ntotal表示节点M出现的状态总数.
内部节点的条件概率可根据历史运行数据进行统计学习.
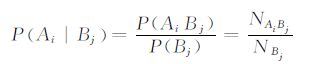
|
其中,PAi|Bj表示节点B状态为j的情况下,节点A状态为i的概率.NAiBj表示A的状态为i,B的状态为j的总次数.NBj表示B的状态为i的总次数.
4 诊断算法基于贝叶斯服务图的错误服务诊断算法(算法1)是指根据所收集的部分异常信息推断出最有可能出现错误的服务.假设集合E={evidence1,evidence2,…,evidencen}是收集到的错误信息的集合,则根据该集合及第3节中参数学习出的先验概率及条件概率,计算出每个服务节点S的后验概率B(S).

|
服务节点的后验概率越高,则表示该服务越可能发生了错误.根据服务节点的后验概率,对服务节点进行降序排序,筛选出前ErrorNumber个最有可能出错的服务节点,对其日志信息进行检测,确定产生错误的服务.
| 算法1 诊断算法 |
| Input:贝叶斯服务依赖图;每个节点及其状态值;收集到的证据集E;错误节点集合ErrorService,初始为空集;阈值ErrorNumber. Output:错误的服务节点集合. |
| 推理计算每个服务执行节点的后验概率B(S); |
| 根据后验概率,对服务节点进行降序排序 |
| 选出前ErrorNumber个服务执行节点Sk |
| 对Sk运行状态日志信息进行检查; |
| If state=error Then |
| ErrorService=ErrorService∪Sk; |
| End If |
| 输出错误节点集合ErrorService |
以图8中购物服务的服务依赖图为例,我们收集平均每个服务的近万条调用日志记录信息,根据第3节中参数训练方法,得到图8中每个数据节点、控制节点及服务节点的条件概率或先验概率.表1所示为服务节点C的先验概率表,表2所示为控制节点c′的条件概率表,其中左栏为节点C,b′,c的各种取值状态,右栏为节点c′对应的3种状态(T,F,┬)的概率值.
| C | b′ | c | c′ | ||
| T | F | ┬ | |||
| T | T | Input(b) | 0.48 | 0.39 | 0.13 |
| T | T | ┬ | 0.03 | 0.90 | 0.07 |
| T | F | Input(b) | 0.41 | 0.15 | 0.44 |
| T | F | ┬ | 0.41 | 0.08 | 0.52 |
| T | ┬ | Input(b) | 0.80 | 0.02 | 0.18 |
| T | ┬ | ┬ | 0.05 | 0.21 | 0.74 |
| F | T | Input(b) | 0.07 | 0.15 | 0.79 |
| F | T | ┬ | 0.09 | 0.36 | 0.55 |
| F | F | Input(b) | 0.09 | 0.28 | 0.63 |
| F | F | ┬ | 0.17 | 0.50 | 0.33 |
| F | ┬ | Input(b) | 0.11 | 0.10 | 0.79 |
| F | ┬ | ┬ | 0.00 | 0.03 | 0.97 |
| ┬ | T | Input(b) | 0.02 | 0.92 | 0.06 |
| ┬ | T | ┬ | 0.19 | 0.23 | 0.58 |
| ┬ | F | Input(b) | 0.03 | 0.94 | 0.03 |
| ┬ | F | ┬ | 0.24 | 0.68 | 0.08 |
| ┬ | ┬ | Input(b) | 0.65 | 0.00 | 0.35 |
| ┬ | ┬ | ┬ | 0.16 | 0.06 | 0.78 |
收集的证据信息显示服务C输出异常即f′=F.按照4中的诊断算法,推理服务节点A,B,C 发生异常的概率即A,B,C的后验概率如表3所示.
由服务节点A、B、C的后验概率看出服务节点A最有可能发生了异常,检测服务节点A的日志信息,发现A确实发生了错误.
为了更加精确地验证本文算法的准确度和有效性,我们采用模拟实验的方式扩大了节点的规模.条件概率描述了节点状态间的概率关联,这种关联在不同的组合中是随机变化的,因此我们可以随机模拟生成条件概率表.同时为了进行异常诊断,我们会按相关节点的状态及条件概率表模拟服务异常节点的生成.
为了定量研究算法的准确度,我们定义评价因子故障诊断准确度(FDA,Fault Diagnosis Accuracy):
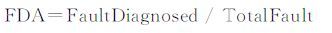
|
其中,TotalFault表示所有的故障数,FaultDiagnosed表示诊断出的故障的数目.
仿真实验中,随机生成服务节点数为10,30,50,70的不同规模的复合服务,对于每种规模的复合服务,会随机生成10个不同流程结构的复合服务,并将随机生成的复合服务模型转换为相应的贝叶斯网络模型.同时,需要为贝叶斯网络中的每个节点进行参数赋值.对于贝叶斯网络中每个服务执行节点,按均匀分布随机生成其先验概率,区间为[0.8,0.9].对于每个数据节点和控制节点,无论是内部节点还是非内部节点,都采用随机的方式生成其先验概率或条件概率.为了模拟各个服务节点异常的生成,随机生成随机数D,取值区间为[0,1],如果D小于服务执行节点的先验概率,则服务节点执行正常,否则执行错误.同时,数据节点和控制节点的状态也通过将一个随机生成的数与由相关的节点的状态及条件概率表决定的条件概率进行比较来确定.模拟中,记录所有输出节点的状态,但只使用30%~70%的输出节点状态作为观察证据,对每个网络,共进行100次实验,并计算平均FDA.
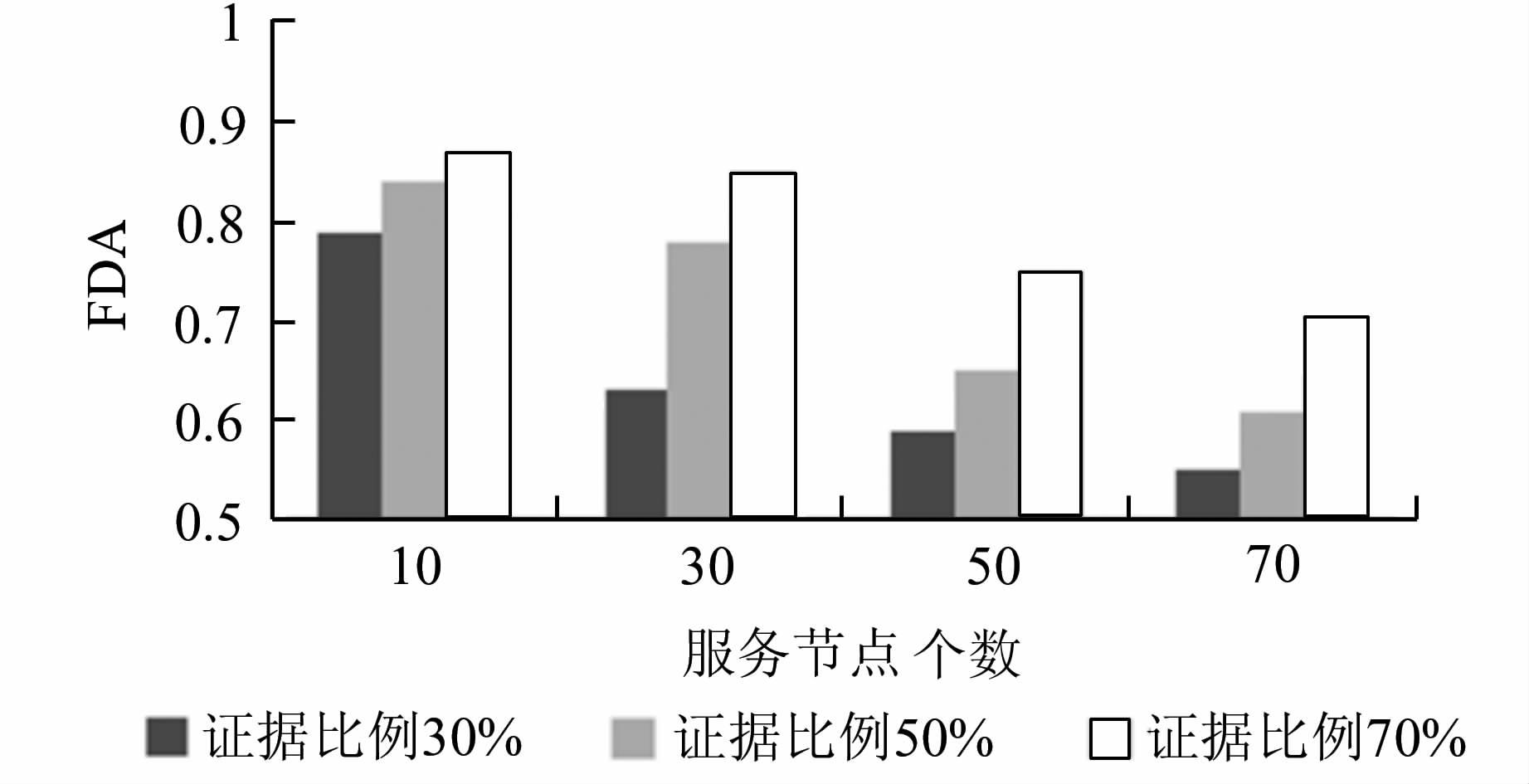
图9所示是在不同的证据比例30%,50%,70%下,针对服务节点数分别为10,30,50,70的不同规模的复合服务进行模拟实验所得的FDA的实验结果.
根据图9所示的结果,可以看出,服务节点的个数越少,证据的比例越高,则算法的准确度越高.
|
| 图 9 不同规模(10,30,40,50)的复合服务及不同证据比例(30%,50%,70%)下FDA的仿真结果 Figure 9 FDA under the circumstance of composite services size ranging in (30,40,50) and evidence proportionranging in (30%,50%,70%) |
本文提出了一个基于贝叶斯服务依赖图的错误定位方法.与以往错误服务诊断方法相比,本方法充分考虑了复合服务中的数据依赖关系和控制依赖关系.本文详细介绍了服务组合流程中四种基本组合结构向贝叶斯服务依赖图的转换过程.贝叶斯服务依赖图生成以后,通过查询服务的历史记录,将组件服务的可靠性作为服务执行节点的先验概率,并通过统计参数学习的方式计算非服务执行节点的先验概率或条件概率.之后,提出了服务的诊断算法,并通过模拟实验验证了算法的有效性.然而服务组合中,除了数据依赖和控制依赖,可能还存在其他潜在的依赖关系,为进一步提高错误服务诊断的准确度,发现和挖掘其他潜在的依赖关系将成为今后工作的研究方向.
| [1] | 夏永霖.复合服务自恢复关键技术研究[D]. 合肥:中国科学技术大学, 2010. XIA Y L. Research on Key Techniques of Self-Recovery for Service Composition [D]. Hefei: University of Science and Technology of China锛?2010(Ch). |
| [2] | KIM S M, ROSU M C. A survey of public web services[DB/OL].[2015-02-20].http://link.springer.com/chapter/10.1007/978-3-540-30077-9_10 #page -1. |
| [3] | JIANG W, HU S, LEE D,et al . Continuous query for QoS-aware automatic service composition[DB/OL].[2015-01-20].http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6257789&tag=1. |
| [4] | ARDISSONOL, CONSOLE L, GOY A,et al . Enhancing web services with diagnostic capabilities[DB/OL].[2015-02-10].http://ieeexplore.ieee.org/xpls/abs_all.jsp ?arnumber =1595728. |
| [5] | GROSCLAUDE I. Model-based monitoring of component-based software systems[DB/OL].[2015-02-15].http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1 .1 .7593&rep =rep &type =pdf . |
| [6] | LIANG Q A, SU S Y W. AND/OR graph and search algorithm for discovering composite web services[J]. International Journal of Web Services Research \1(IJWSR \1), 2005, 2 (4) : 48 –67. |
| [7] | GU Z F, Li J X, XU B. Automatic service composition based on enhanced service dependency graph[DB/OL].[2015-01-10].http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber =4670182. |
| [8] | 朱明敏. 贝叶斯网络结构学习与推理研究[D]. 西安: 西安电子科技大学, 2013. ZHU M M. Research on Structural Learning and Inference in Bayesian Networks \1[D]. Xi’an: Xidian University,2013(Ch). |
| [9] | 余长慧, 孟令奎, 潘和平. 基于贝叶斯网络的不确定性知识处理研究[J]. 计算机工程与设计, 2004 ,25 (1) : 1 –3. YU C H, MENG L K, PAN H P. Research on handling uncertain knowledge based on Bayesian network[J]. Computer Engineering and Design, 2004, 25 (1) : 1 –3. |
| [10] | 张岩. 概率图模型及其推理技术的研究现状[J]. 信息技术, 2013 ,37 (5) : 91 –93. ZHANG Y. Survey on probability graph model and its reasoning technology[J]. Information Technology 1, 2013, 37 (5) : 91 –93. |
| [11] | 王飞, 邹仕洪, 陈山枝, 等. 基于模糊数学的 Web 服务QoS建模[J]. 计算机应用研究, 2007 ,24 (4) : 214 –216. WANG F, ZOU S H, CHEN S Z, et al. Understanding and modeling of Web services QoS[J]. Application Research of Computers 1, 2007, 24 (4) : 214 –216. |
| [12] | 范小芹, 蒋昌俊, 王俊丽, 等. 随机QoS感知的可靠Web服务组合[J]. 软件学报, 2009 ,20 (3) : 546 –556. FAN X Q, JIANG C J, WANG J L, et al. Random-QoS-Aware reliable Web service composition[J]. Journal of Software 1, 2009, 20 (3) : 546 –556. |
 2016, Vol. 62
2016, Vol. 62





