文章信息
- 王丽娜, 谭选择, 徐一波, 翟黎明
- WANG Lina, TAN Xuanze, XU Yibo, ZHAI Liming
- 基于纹理复杂度的JPEG图像自适应隐写
- An Adaptive JPEG Image Steganography Based on Texture Complexity
- 武汉大学学报(理学版), 2017, 63(5): 421-426
- Journal of Wuhan University(Natural Science Edition), 2017, 63(5): 421-426
- http://dx.doi.org/10.14188/j.1671-8836.2017.05.006
-
文章历史
- 收稿日期:2016-08-25

2. 武汉大学 计算机学院, 湖北 武汉 430072
2. School of Computer, Wuhan University, Wuhan 430072, Hubei, China
隐写术是一种利用载体的掩蔽效应将秘密信息隐藏,实现信息秘密传递的技术.隐写载体可以是图像、音频、视频、文本等网络数字媒体.由于JPEG已成为目前互联网上进行图像传输时最常用的图像格式,因此以JPEG图像作为载体的隐写研究也成为了图像隐写领域的热点.
通过修改载体图像空域或频域的LSB(lest significant bit)位即可以实现最简单的隐写,这种修改会造成图片像素或DCT系数统计频率中相邻值对趋于一致,为了避免这种现象,LSB匹配(MLSB)被提出.为了进一步提升隐写算法性能,编码技术被引入隐写过程.文献[1]将隐写术抽象成一个特殊的编码问题,包含两个核心部分:载体特性和隐写的编码问题.针对隐写的编码问题,矩阵编码被提出来,它能够有效降低嵌入对载体bit的修改,从而提升隐写算法安全性.例如:引入了矩阵编码的思想的F5算法[2],大大提高了隐写编码的效率.然而,矩阵编码仅仅解决了降低修改率的问题,并未考虑隐写位置与隐写安全性之间的相关性.事实上,隐写载体中,部分位置的隐写具有很好的隐藏效果,而另一些位置的隐写将会大大增加风险.湿纸编码[3]能够将载体中风险较大的嵌入位置标记为湿点,从而在隐写过程中跳过这些危险的嵌入位置,实现隐写算法安全性提升.正是基于这样的编码优势,文献[4]提出了nsF5算法,解决了F5隐写中产生的收缩问题.
矩阵编码和湿纸编码都提升了隐写算法的安全性,但是在可隐写的位置范围内,所有隐写位置被等风险对待.也就是说,隐写算法尚未达到一种最低代价的隐写路径.随着STCs编码[5]的出现,这一问题得到了很好解决.STCs算法将卷积编码和维特比算法结合起来,通过针对载体的特性设计不同的失真模型,并据此选择嵌入信息的位置.一方面,在隐写嵌入率较小的情况下,STCs编码有着极高的编码效率,可大大降低隐写修改率;另一方面,STCs可以寻找一条近似最低代价的修改路径,实现失真最小化.因此,STCs隐写框架下的算法仅仅需要设计一个失真数学模型即代价函数,即可极大提升隐写算法安全性.该编码方法也是目前隐写算法最好的编码,而代价函数的设计成为STCs隐写中的核心问题.
基于STCs隐写方法的代价函数可以针对特定的隐写分析方法设计,如HUGO算法[6]根据SPAM[7]隐写分析方法提取的特征针对性地设计失真代价函数,将失真定义为三阶共生矩阵的权重,对SPAM具有很强的抗检测能力.也可以利用JPEG图像DCT系数的统计特性等设计代价函数,如文献[8]利用JPEG图像量化中出现的量化误差和在DCT分块中各系数出现的频率不同来定义非零DCT系数改动对图像载体的具体失真影响.其他的代价函数设计,如文献[9]使用Canny边缘检测的思想划分边缘区域,刻画不同区域的嵌入失真.文献[10~12]分别从不同的角度基于载体自身的内容特性设计相应的嵌入方法,使嵌入引起的载体失真最小化.
与上述隐写分析方法不同,本文针对图像的纹理特性,设计了一种自适应隐写算法,同时,将均匀嵌入[13]的思想引入,摆脱隐写嵌入在DCT系数绝对值为0附近改动较大的缺点,提高算法的安全性.
1 相关工作 1.1 纹理特征描述图像的纹理分析方法有很多,利用灰度共生矩阵研究纹理特征是其中比较经典的方法之一.
设图像的灰度级为N,则对应该图像的灰度共生矩阵K为N阶矩阵,在矩阵中处于第i行第j列的值代表在图像的灰度矩阵中灰度值为i的元素和灰度值为j的元素在距离为(Δx, Δy)的情况下成对出现的次数,记为pΔx, Δy(i, j).基于灰度共生矩阵,可以从反差和熵两个方面提取纹理特征.
1) 反差
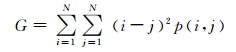
|
(1) |
反差主要用于表征图像的纹理的粗细程度,能够在一定程度上表现出图像的清晰程度.对于纹理较粗的图像,p(i, j)会主要出现在灰度共生矩阵的主对角线附近的位置,此时(i-j)值比较小,对应式中的G值也会比较小,反之在纹理比较细的图像中G值就会比较大.
2) 熵
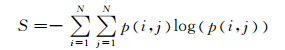
|
(2) |
熵用于表征图像中纹理出现的随机性.当图像的灰度共生矩阵中p(i, j)值都相同时,S值达到最大,此时图像显得比较平滑,当p(i, j)值完全不相同的时候,S值达到最小,此时图像显得比较复杂.
1.2 基于STCs编码的最小失真框架基于STCs编码的最小失真框架是目前最为流行的隐写设计框架,它将隐写设计的重心转移到了对图像失真代价函数的设计上来.
设原始和嵌入信息后的JPEG载体图像的量化DCT系数的LSB分别为x和y,其中x=(x1, x2, x3, …, xn)∈0, 1n,y=(y1, y2, y3, …, yn)∈0, 1n,n为图像像素总个数.假设嵌入操作是二元性的,即对于每一个载体元素来说,只会产生两种处理方式:完全不作改动或产生一个特定大小的变化.对于一个载体元素xi而言,对它作改动所引起的失真定义为ρi,其中ρi∈[0, +∞),即单个元素的失真代价.那么完成嵌入后的总体失真D(x, y)可表示为:
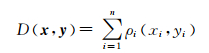
|
(3) |
即所有改动引起的失真代价之和.
采用合适的ρi作为失真测度定义可以最小化嵌入对于载体在统计特征上的变化,增强隐写的抗检测性.在F5隐写中使用矩阵编码已经能够在一定程度上解决这个问题,然而在F5编码方法中其ρi被限制为1,而STCs编码能够在更一般的失真定义下进行编码过程. STCs编码过程可以表示为:
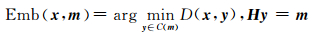
|
(4) |
其中x为载体信息流,m为秘密信息流,y为载密信息流,D(x, y)为失真函数,C(m)为m的陪域,H为校验矩阵.即找到合适的载密信息流y,使得失真代价最小.
1.3 均匀嵌入失真现有的许多自适应算法,在进行信息嵌入时,改动的DCT系数的绝对值一般在0附近.这样的特点容易被隐写分析所利用.为了减弱这种特点,有学者提出了均匀嵌入的思想,设计均匀嵌入失真函数(uniform embedding distortion,UED)[13]如下:
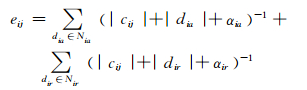
|
(5) |
其中cij是(i, j)位置的DCT系数,αia和αir是为了满足相加的性质而设置的调整参数,Nia和Nir分别表示cij的块内和块间相邻系数.Nia={ci+1, j, ci-1, j, ci, j+1, ci, j-1},即与cij直接相邻的4个系数,Nir={ci+8, j, ci-8, j, ci, j+8, ci, j-8},即cij相邻块的4个系数.考虑到cij可能处于图像的边界上,此时邻近系数不存在的点不计入计算.
2 本文方法 2.1 失真代价函数分析设计JPEG图像压缩前,先将RGB图像转换为YCrCb图像,并对图像进行8×8分块.如果原始的图像的长宽不是8的倍数,需要先补成8的倍数,使其能够进行同等处理.基于以上JPEG图像压缩的特点,本文在度量图像的局部纹理复杂度时,也选取8×8块作为复杂度的计算单元.
文献[14]分析了6个纹理特征,其中,反差和熵被认为是对纹理复杂性描述效果上最重要的两个参数.本文在描述图像的局部纹理复杂度时,使用反差和熵两个参数.本文方法分别对每个分块补完之后的8×8矩阵求其灰度共生矩阵,用下式度量此分块矩阵的纹理复杂度:
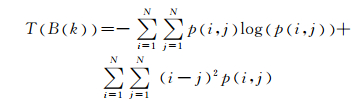
|
(6) |
其中B(k)代表某一个8×8的子块.
在设计隐写嵌入的失真代价时,秘密信息嵌入在越复杂的区域的,抗检测性越强,即T(B(k))的值越大的区域嵌入的安全性越高,则失真定义为:
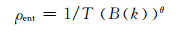
|
(7) |
其中参数θ可设置为2.
在JPEG图像DCT域上进行隐秘信息嵌入,还需要考虑到在量化过程中归整带来的影响.按照Fridrich等在文献[15]中的研究,秘密信息应该嵌入到那些在量化的过程中量化误差为0.5的系数中去.
令ρf表示在嵌入秘密信息和JPEG标准量化过程中产生的误差双重影响下产生的失真影响.假设没有经过JPEG压缩的原图像是已知的,设u和q分别表示量化前DCT系数和该图像压缩对应的量化步长,uq=u/q是进行了量化操作之后的DCT系数,用u来表示量化后进行归整得到的整数DCT系数,有:
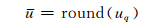
|
(8) |
因归整产生的误差为:
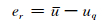
|
(9) |
因此对于整个量化过程产生的误差可表示为:
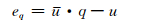
|
(10) |
对于仅使用LSB位的变化进行的嵌入,的u最末位会发生+1或者-1的变化,设v为嵌入之后DCT的值,则变化的关系可以表示为:
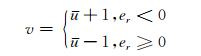
|
(11) |
因此,在知道载体图像原BMP格式数据时,因量化引起的失真可以表示为:
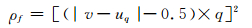
|
(12) |
从(12) 式可以看出,当(|v-uq|-0.5) 的绝对值增大时,ρf就会增大.因为y是整数,因此在嵌入时,我们选择量化误差为0.5的系数进行嵌入,保证(|v-uq|-0.5) 的绝对值最小.上式可以简化为:
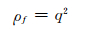
|
(13) |
结合每个块的纹理复杂度失真和不同位置的DCT系数在量化过程中的量化误差,将失真函数综合定义为:
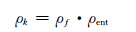
|
(14) |
其中ρk指的是第k个DCT系数的失真定义.
一般来说,均匀嵌入是和STCs编码框架联合在一起进行使用的.均匀嵌入方法就是在失真函数的设计中加入某种控制因子,使得在嵌入过程中系数绝对值大小不同的系数被改动的概率会趋近于相同.
根据(5) 式,在均匀嵌入中用e(i, j)来表示此处的在这个系数上进行嵌入的失真测度.得到针对DCT系数的嵌入失真函数:
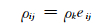
|
(15) |
其中ρk描述(i, j)位置系数所处的分块.
2.2 嵌入与提取过程1) 嵌入过程.
(a)将JPEG图像解压缩成灰度图像,对该灰度图进行类似JPEG标准压缩算法中的8×8分块.
(b)针对每一个块,利用(6) 式和(7) 式计算出基于每个块的失真代价.
(c)提取出该JPEG图像所用的量化表,按照(13)、(14) 和(15) 式,并结合(b)中得到的每个块的失真代价,计算出每一个DCT系数的失真代价.
(d)按照先块内行扫描再块间行扫描的方式,取出值为非0的DCT系数中的AC系数的LSB,形成比特流,然后对此比特流进行置乱操作,得到置乱后的比特流c.
(e)利用STCs编码和已经设计好的失真代价函数将要嵌入的隐秘信息比特流m嵌入到比特流c中,得到载密比特流s,将s按照密钥key进行恢复原始顺序,将s比特流和原DCT系数相结合得到载密的DCT系数.
(f)对载密的DCT系数进行熵编码等JPEG压缩标准中的后续操作形成JPEG图像,完成秘密信息嵌入过程,得到载密图像.
2) 提取过程.
(a)提取出载密图像的DCT系数,按照先块内再块间的行扫描方式得到非0的DCT系数中的AC系数,然后取其LSB位形成比特流s.
(b)利用密钥key对比特流s进行置乱,然后结合STCs编码的提取过程进行计算得到秘密信息比特流m,完成整个提取过程.
3 实验结果 3.1 实验准备本文中使用的实验嵌入工具是Matlab 2013b,分类器为SVM(support vector machine),实验中所用图像来自于UCID[16]图像库, 选择经典的nsF5、MB[17]和STC-Const[18]算法进行比较实验,为了验证隐写方法的安全性,从两个方面来进行评价:1) 视觉感知性;2) 抗隐写检测能力.
3.2 视觉感知性分析从图像库中随机选取12张灰度图像,在0.3 bpac(bits per non-zero AC DCT coefficient)和0.5 bpac嵌入率下对原始图像进行秘密信息嵌入形成载密图像,对不同隐写算法形成的载密图像PSNR进行比较,结果如表 1.
| dB | ||||
| 嵌入率/bpac | 本文方法 | MB | nsF5 | STC-Const |
| 0.3 | 46.43 | 42.83 | 44.86 | 45.38 |
| 0.5 | 41.55 | 40.23 | 41.43 | 41.23 |
从表 1可以看到,在嵌入率相对较低的情况下本文算法在视觉感知性上的隐蔽程度较另三种算法更高一些.
3.3 抗检测能力分析选择高维的CFstar[19]特征以及CCJRM[20]特征对采用不同嵌入率进行嵌入的载密图像进行隐写分析.
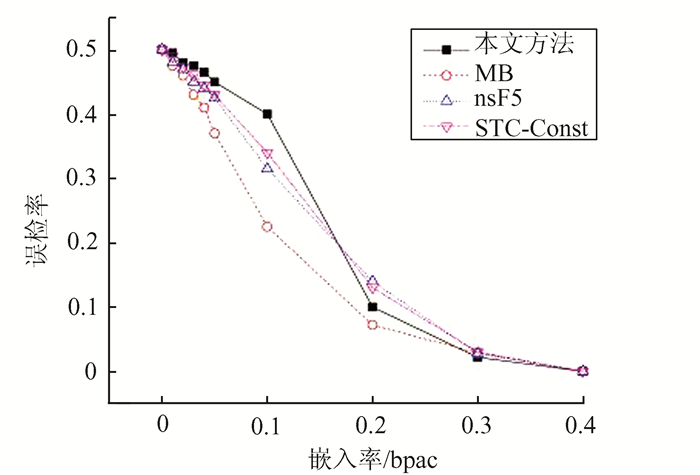
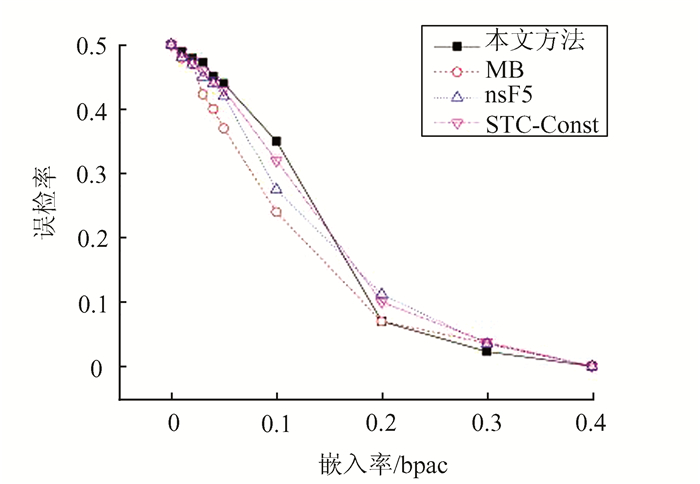
在UCID图像库中选取1 338张图像,并按照不同的嵌入率进行嵌入,分别形成载密图像,然后随机选取其中669张未嵌入图像和669张相应的嵌入图像用于对分类器进行训练,剩下的一半图像用于测试.在实验中对图像进行嵌入率分别为0.01,0.02,0.03,0.04,0.05,0.1,0.2,0.3,0.4 bpac的信息嵌入.如图 1和2.
|
| 图 1 在CFstar特征下误检率 Figure 1 Error rate in using CFstar |
|
| 图 2 在CCJRM特征下误检率 Figure 2 Error rate in using CCJRM |
从图 1和图 2可以看出,当嵌入率小于0.1 bpac时,本文算法的误检率较另三个算法中更大,即本文算法是相对更安全的算法.当嵌入率进一步提高的时候,所有算法误检率会迅速地降低.较另三种算法,本文算法下降幅度更大.其原因可能来自于两个方面,首先,在算法中使用基于块来定义复杂程度,当嵌入率处于比较高的水平的时候这种度量失真的方式可能已经不太适用;其次,STCs编码方法本身在嵌入率上升时其抗检测能力也会随之降低.
使用尺寸为512×512,量化因子为80的Lena灰度JPEG图像作为载体,来说明基于图像纹理自适应嵌入的特点.为了让改动位置更多,得到的修改位置图能够看得更明显,选择嵌入率为0.5 bpac的载密图像进行对比.从图 3可以看出,进行嵌入时改动的位置都是处于图像中纹理相对复杂的局部区域,达到了基于纹理自适应嵌入的目标.

|
| 图 3 基于图像纹理自适应嵌入的特点 Figure 3 Characteristic of texture-based adaptive embedding |
在没有进行均匀嵌入思想的算法中,嵌入后系数值发生变化主要集中在系数本身绝对值为0附近,并且随着系数绝对值的增大发生改动的系数个数越来越少.而在进行了均匀嵌入的算法中,对各个绝对值不同的系数进行改动个数应该相近.为了验证算法中是否体现了均匀嵌入的特征,选用nsF5和本文算法作对比,使用512×512的Lena灰度图在嵌入率为0.3 bpac下进行嵌入,分别对两种算法中DCT不同系数的改动个数进行统计,为了能够更明显地观察到变化,在直方图中选取区别比较明显的[-20,20]区间进行比较.
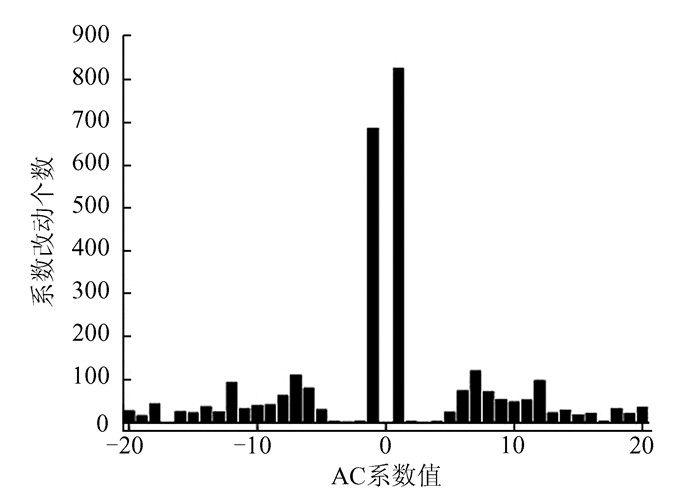
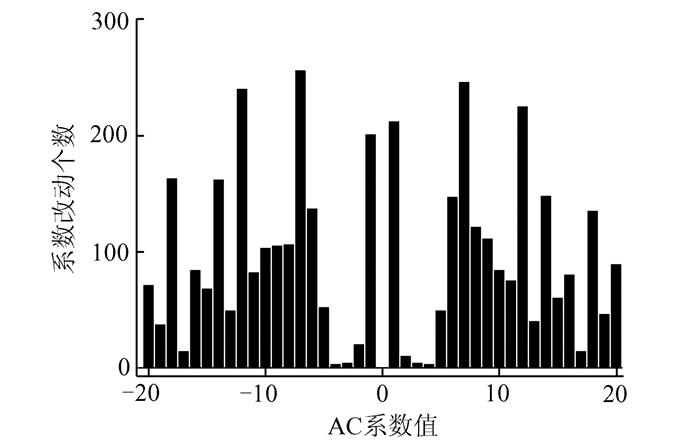
图 4和图 5为嵌入率为0.3 bpac时嵌入后图像的DCT系数中改动值的分布情况,从中可以看出,本文算法中引入均匀嵌入思想,使得在嵌入秘密信息时对嵌入的DCT系数的分布做了均匀化,改动的DCT系数个数没有集中在绝对值为0附近,而是相对分散,在不同绝对值的DCT系数改动个数相差较小.
|
| 图 4 nsF5算法嵌入时改动DCT系数值分布 Figure 4 DCT coefficient modified using nsF5 |
|
| 图 5 本文算法嵌入时改动的DCT系数分布 Figure 5 DCT coefficient modified using proposed algorithm |
利用STCs编码进行隐写,涉及到的失真代价函数设计丰富多样,本文采用图像纹理复杂度函数作为失真代价函数,与一般的内容自适应隐写相比,由于直接使用与图像纹理密切相关的纹理描述函数作为考量,能够充分利用复杂纹理带来的掩蔽效果,所以实验效果较好.在实际应用中,为了达到更好的隐藏效果,隐写的嵌入率一般设置较小,而在嵌入率相对较小的情况下,本文方法更具有优势.
尽管由图像纹理复杂度所设计的失真代价函数能够带来较好的隐蔽效果,但其太过依赖图像的纹理特性,对于一些纹理平滑的图片,其嵌入容量往往较低.因此,将图像纹理失真与针对特定应用场景的失真结合起来,在提高嵌入容量的同时考虑到图像纹理的安全性将是本文的一个重要研究方向.同时,由于图片纹理描述方式的多样性,研究不同纹理描述方式所带来的影响效果,并进一步根据不同场景图片选择效果较好的纹理描述方式来进行代价函数的设计,提高隐写安全性是本文的另一个重要研究方向.
| [1] |
ZHANG W, LI S. A coding problem in steganography[J]. Designs, Codes and Cryptography, 2008, 46(1): 67-81. DOI:10.1007/s10623-007-9135-9 |
| [2] |
WESTFELD A. F5-A steganographic algorithm[C]//International Workshop on Information Hiding. Berlin:Springer, 2001:289-302. http://www.springerlink.com/content/vx1792h1a9xe3xe2
|
| [3] |
奚玲, 平西建, 张涛. 一种新的湿纸码自适应信息隐藏方法[J]. 应用科学学报, 2010, 28(5): 485-492. XI L, PING X J, ZHANG T. A new adaptive steganography using wet paper code[J]. Journal of Applied Sciences, 2010, 28(5): 485-492. |
| [4] |
FRIDRICH J, PEVNY T, KODOVSKY J. Statistically undetectable jpeg steganography:Dead ends challenges, and opportunities[C]//Proceedings of the 9th Workshop on Multimedia & Security. New York:ACM, 2007:3-14. http://dl.acm.org/citation.cfm?id=1288872
|
| [5] |
FILLER T, JUDAS J, FRIDRICH J. Minimizing additive distortion in steganography using syndrome-trellis codes[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(3): 920-935. DOI:10.1109/TIFS.2011.2134094 |
| [6] |
PEVNY T, FILLER T, BAS P. Using high-dimensional image models to perform highly undetectable steganography[C]//International Workshop on Information Hiding. Berlin:Springer-Verlag, 2010:161-177. http://link.springer.com/10.1007/978-3-642-16435-4_13
|
| [7] |
PEVNY T, BAS P, FRIDRICH J. Steganalysis by subtractive pixel adjacency matrix[J]. IEEE Transactions on Information Forensics and Security, 2010, 5(2): 215-224. DOI:10.1109/TIFS.2010.2045842 |
| [8] |
WANG C, NI J. Design of Adaptive Steganographic Schenes for Digital Images[DB/OL].[2016-02-02]. http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=731809.
|
| [9] |
韩涛, 祝跃飞. 基于Canny边缘检测的自适应空域隐写术[J]. 电子与信息学报, 2015, 37(5): 1266-1270. HAN T, ZHU Y F. Adaptive spatial steganography based on Canny's edge detection[J]. Journal of Electronics & Information Technology, 2015, 37(5): 1266-1270. DOI:10.11999/JEIT141121 |
| [10] |
SEDIGHI V, COGRANNE R, FRIDRICH J. Content-adaptive steganography by minimizing statistical detectability[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(2): 221-234. DOI:10.1109/TIFS.2015.2486744 |
| [11] |
PARK T H, HAN J G, EOM I K. Steganalysis of content-adaptive steganography using Markov features for DCT coefficients[J]. Journal of the Institute of Electronics and Information Engineers, 2015, 52(8): 97-105. DOI:10.5573/ieie.2015.52.8.097 |
| [12] |
MUNGMODE S, SEDAMKAR R R, KULKARNI N. A modified high frequency adaptive security approach using steganography for region selection based on threshold value[J]. Procedia Computer Science, 2016, 79: 912-921. DOI:10.1016/j.procs.2016.03.114 |
| [13] |
GUO L, NI J, SHI Y Q. Uniform embedding for efficient JPEG steganography[J]. IEEE Transactions on Information Forensics and Security, 2014, 9(5): 814-825. DOI:10.1109/TIFS.2014.2312817 |
| [14] |
BARALDI A, PARMIGGIANI F. An investigation of the textural characteristics associated with gray level cooccurrence matrix statistical parameters[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(2): 293-304. DOI:10.1109/36.377929 |
| [15] |
FRIDRICH J, GOLJAN M, SOUKAL D. Perturbed quantization steganography[J]. Multimedia Systems, 2005, 11(2): 98-107. DOI:10.1007/s00530-005-0194-3 |
| [16] |
SCHAEFER G, STICH M. UCID:An Uncompressed Color Image Database[DB/OL].[2016-03-02].http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=837905.
|
| [17] |
SALLEE P. Model-based methods for steganography and steganalysis[J]. International Journal of Image and Graphics, 2005, 5(1): 167-189. DOI:10.1142/S0219467805001719 |
| [18] |
FARINHA T, FONSECA I, SIMOES A, et al. Minimizing embedding impact in steganography using trellis-coded quantization[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2010, 6(1): 175-178. |
| [19] |
KODOVSKY J, FRIDRICH J, HOLUB V. Ensemble classifiers for steganalysis of digital media[J]. IEEE Transactions on Information Forensics & Security, 2012, 7(2): 432-444. |
| [20] |
FRIDRICH J, FRIDRICH J. Steganalysis of JPEG Images Using Rich Models[DB/OL].[2016-04-02].http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=1284476.
|
 2017, Vol. 63
2017, Vol. 63




