文章信息
- 汪慎文, 谢承旺, 郭肇禄, 王培崇, 张翠军
- WANG Shenwen, XIE Chengwang, GUO Zhaolu, WANG Peichong, ZHANG Cuijun
- 集成两变异策略的差分进化算法
- Differential Evolution Algorithm Integrated Bi-Mutation Strategy
- 武汉大学学报(理学版), 2019, 65(3): 238-242
- Journal of Wuhan University(Natural Science Edition), 2019, 65(3): 238-242
- http://dx.doi.org/10.14188/j.1671-8836.2019.03.002
-
文章历史
- 收稿日期:2018-02-03

2. 河北地质大学 人工智能与机器学习研究室,河北 石家庄 050031;
3. 南宁师范大学 计算机与信息工程学院,广西 南宁 530299;
4. 江西理工大学 理学院,江西 赣州 341000
2. Laboratory of Artificial Intelligence and Machine Learning, Hebei GEO University, Shijiazhuang 050031, Hebei, China;
3. School of Computer and Information Engineering, Nanning Normal University, Nanning 530299, Guangxi, China;
4. School of Science, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China
差分进化(differential evolution,DE)算法[1]是一种高效的全局智能搜索算法,适合求解初始解与最优解存在较长的搜索距离的优化问题。与其他进化算法相比操作步骤大致相同,DE也包含初始化、变异、杂交和选择等操作;不同之处在于,借助个体差分量对基础个体加以扰动,DE具有较强的自适应搜索能力[2]。正是由于这一点,使得DE在很多优化问题的求解中表现出优越的性能,多次在国际演化比赛力压群雄,拔得头筹。
近年来,研究人员从多个角度不断改进DE算法。文献[3]把DE大体分为三类:1)操作策略的改进(如:三角变异策略[4]、精英变异策略[5]等),其中也包含调参方法研究(如:jDE[6]、FADE[7]、JADE[8]、文献[9]等);2)差分进化静态集成,如:与反向学习策略集成ODE[10]、与EDA集成的DE/EDA[11]、与PSO集成的PSO-DE[12]等。该类算法主要特征是集成优良特质策略来改进DE算法性能。在这类静态集成算法中,静态知识主要应用于策略选取或策略执行次数确定两方面,但是不足之处主要体现在不能“因问题施策略”,导致计算开销增大的可能性;3)差分进化动态集成,如:EPSDE[13]、SaDE[14]等。该类算法主要特征是融入策略选择学习机制,对进化过程中的所选用的变异策略进行评估,其结果用于优化个体的策略选择。在这类动态集成算法中,动态知识主要应用于针对不同的优化问题在进化的不同阶段选择最合适的变异策略,不足之处是因学习机制而存在额外计算开销,而且策略选择是否妥当依赖于学习机制的学习能力。
通过对文献进行梳理不难发现,集成算法特别是动态集成,是差分进化算法,甚至是随机搜索算法的研究热点。构造一款轻计算的差分进化动态集成算法一直是研究者孜孜不倦的追求。为此,本文提出动态集成两个变异策略的差分进化算法(differential evolution algorithm integrated bi-mutation strategy,DE -BMS)。该算法集成两个优势互补的变异策略并动态执行,力求在全局搜索和局部搜索中寻找平衡。
1 本文的思路及算法DE-BMS算法思想在于:首先选取变异策略,然后个体根据策略选择概率动态配置一个变异策略产生后代。为此,本文集成机制主要涉及策略选取和策略动态机制设计两部分。
1.1 变异策略选取选取在设计DE算法时频繁使用的两个变异策略,其分别为:
1)DE/rand/1/bin,由DE/rand/1变异策略和二项式交叉联合组成。
2)DE/best/1/bin,由DE/best/1变异策略和二项式交叉联合组成。
策略DE/rand/1因在搜索方向和搜索距离上均无偏性,使得算法具有较强的勘探能力;策略DE/ best/1通过向种群最好个体的学习,提升算法的开采能力。
1.2 变异策略动态执行机制在个体变异过程中,对每一个体随机赋一个0到1之间的随机数,如果随机数小于选择概率Ps,则执行DE/rand/1,否则执行DE/best/1。用公式表示如下

|
(1) |
个体在变异过程中,通过DE/rand/1和DE/best/1相互配合又相互竞争而使其具备兼顾勘探和开采的均衡搜索能力。在进化过程中陷入搜索空间的某个超平面而仅靠DE/best/1不能摆脱时,采用DE/rand/1有助于逃离。但是通过DE/best/1已形成所期望的积木块时,可能会被DE/rand/1破坏。如何有效地配合使用这两个变异策略,选择概率Ps尤其重要。
1.3 DE-BMS算法算法框架与传统DE算法相同,惟一不同之处在于个体所使的变异策略是动态变化。
设D 为个体的维数,NP为种群规模,t 为进化代数,F 为缩放因子,Cr为杂交概率,MaxFEs为最大评估次数,VTR为预定义精度,Ps为个体策略选择概率,xi,j(t)表征第t 代种群中第i 个体第j 维上的值,Lj和Uj分别为个体第j 维的左边界和右边界,νi,j (t)为变异个体Vi(t)在第j 维上的取值,jrand是在区间[1,D]中随机选择的整数。
在初始化阶段,每个个体在每一维上的取值xi,j (t)为介于左边界和右边界的一个随机值。在变异阶段,从种群中随机选择两个个体,求其差值并进行缩放,其量作为第三个随机个体或最优个体xb(t)的扰动量。在杂交阶段,按照一定杂交概率Cr,对于每一维从种群个体和变异个体中二者选其一。在选择阶段,从种群个体和杂交个体中选择最优个体保留到下一代中。算法伪代码如下。
| 算法1 集成两变异策略的差分进化算法DE⁃BMS |
| 1) 参数初始化:NP,t=0,D,F,Cr, FEs=NP |
| 2) 初始化:xi, j (t)= Lj + rand(U j - Lj) |
| 3) while FEs < MaxFEs and abs(Min(fit)) > VTR |
| 4) for i=1 to NP |
| 5) 配置:每一个体X i (t)分配一个变异策略动态执行随机值r i; |
| 6) 变异:对个体用(1)式进行突变 |
| 7) 修补:对越界个体用如下公式 |
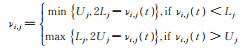 |
| 8) 杂交:种群个体杂交用如下公式 |
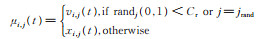 |
| 9) 选择:对个体用竞争选择 |
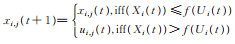 |
| 10) t=t+1, FEs=FEs+NP |
| 11) end for |
| 12) end while |
为了研究DE-BMS算法的性能,本文选择了13个经典基准函数进行测试。关于13个经典基准函数的详细描述,参考文献[15]。实验主要包括三个方面内容:1)变异策略参数的选取;2)与其他差分进化算法的收敛速度和成功次数比较;3)与其他差分进化算法的解质量比较。
本文使用的仿真实验平台:Windows 7操作系统,Intel 3.16 GHz双核处理器,4 GB内存,Matlab 2010。
实验中各算法参数相同。种群规模(NP)设为30,测试函数维数(D)被设置为30。考虑到算法的随机性,每个优化问题都以达到最大评价次数(MaxFEs)或者得到预定义精度(VTR)作为终止条件,独立运行(Runs)50次。表 1列出了优化函数的最大评价次数和求解精度,其中:f1~ f4为简单单模函数,f5~ f7为较难单模函数,f8和f9为较难多模函数,f10~ f13为简单多模函数。实验中如没有特指,算法使用的F 为0.8,Cr为0.2。经过大量实验验证,选择概率Ps的合理值为0.5。
| 函数 | MaxFEs | VTR |
| f1 | 2.0E+5 | 1E-50 |
| f2 | 2.0E+5 | 1E-50 |
| f3 | 5.0E+5 | 1E-08 |
| f4 | 5.0E+5 | 1E-10 |
| f5 | 5.0E+5 | 1E-08 |
| f6 | 1.5E+5 | 1E-08 |
| f7 | 3.0E+5 | 1E-03 |
| f8 | 3.0E+5 | 1E-08 |
| f9 | 3.0E+5 | 1E-10 |
| f10 | 1.5E+5 | 1E-10 |
| f11 | 1.5E+5 | 1E-20 |
| f12 | 1.5E+5 | 1E-08 |
| f13 | 1.5E+5 | 1E-08 |
为了验证本文算法的有效性,本文使用三个评价指标来验证算法的收敛速度和求解精度:算法终止时适应度评价次数的平均值(AVER)、独立运行中成功收敛于指定的精度的运行次数(SR)和解质量。
2.1 DE-BMS算法控制参数表 2给出DE-BMS算法在13种不同缩放因子F和杂交概率Cr 下实验统计结果。实验是在13个测试函数50次独立运行后统计的,SR表示在13个测试函数50次独立运行后算法成功收敛的运行次数的平均值。
| F | Cr | SR |
| 0.8 | 0.1 | 33.38 |
| 0.8 | 0.2 | 31.83 |
| 0.8 | 0.3 | 28.42 |
| 0.8 | 0.4 | 23.85 |
| 0.9 | 0.1 | 34.23 |
| 0.9 | 0.2 | 30.01 |
| 0.9 | 0.3 | 23.92 |
| 0.9 | 0.4 | 17.69 |
| 0.7 | 0.1 | 31.38 |
| 0.7 | 0.2 | 29.98 |
| 0.7 | 0.3 | 27.13 |
| 0.7 | 0.4 | 25.62 |
| 1.0 | 0.1 | 32.34 |
| 注:表中数字加粗表示最优值 | ||
从表 2可以看出,在给定F 时(如0.8,0.9,0.7)时,随着Cr的增加,算法成功收敛,SR呈现单调减的趋势。在F 为0.8时,Cr由0.1按照步长0.1递增至0.4时,SR由33.38变化到23.85;在F 为0.9时,Cr由0.1变化到0.4,SR由34.23变化到17.69;同样,在F 为0.7时,SR由31.38变化到25.62。从表 2中可以看出,当F 为0.9,Cr为0.1时,DE-BMS算法的SR最高,说明DE-BMS算法具有更好的鲁棒性。在后面的实验中,DE -BMS算法的F 选择为0.9,Cr选择为0.1。
2.2 与其他DE的收敛速度和成功次数比较表 3给出DE-BMS与其他5个模型(DE/rand/ 1、DE/best/1、SaDE、jDE、文献[9])的实验统计结果。从表 3可以看出,在大多数情况下,DE-BMS所需要的评估次数少于文献[9]、SaDE、DE/rand/1和DE/best/1,高于jDE。说明DE - BMS算法集成DE/rand/1和DE/best/1之后,总体性能均优于只使用DE/rand/1和DE/ best/1变异策略的算法,而弱于其他算法。说明DE-BMS算法集成两策略的优势,使得性能超越于单纯只用一个策略的算法性能,但是由于DE-BMS算法中的/best/1策略在接近于最优值位置时容易被/rand/1策略进行破坏,使得其求解单模函数时性能不如其他集成算法。相比之下,在优化单峰函数问题时尽管DE-BMS算法在4个函数上都不能成功收敛,但是在优化多峰函数问题时均成功收敛,且成功收敛的次数均超过47次,甚至在f10、f11、f12、f13上成功收敛50次。从这里可以看出,DE-BMS算法在优化多峰函数问题更有普适性,这要归功DE-BMS算法中/rand/1策略可以在多个山峰中跳转而找到包含最优位置的山峰,而/best/1策略去接近于最优位置。
| 函数 | AVER/SR | |||||
| DE/rand/1 | DE/best/1 | SaDE | jDE | 文献[9] | DE⁃BMS | |
| f1 | 2.00E+05/00 | 1.54E+05/50 | 9.80E+04/50 | 7.98E+04/50 | 6.67E+04/50 | 1.90E+05/50 |
| f2 | 2.00E+05/00 | 2.00E+05/00 | 1.38E+05/50 | 1.27E+05/50 | 2.31E+05/50 | 2.00E+05/00 |
| f3 | 5.00E+05/00 | 5.00E+05/00 | 3.69E+05/50 | 2.10E+05/50 | 3.34E+05/50 | 5.00E+05/00 |
| f4 | 4.53E+05/50 | 2.41E+05/50 | 4.21E+05/32 | 5.00E+05/00 | 3.51E+05/23 | 4.13E+05/50 |
| f5 | 5.00E+05/00 | 5.00E+05/00 | 5.00E+05/00 | 2.82E+05/42 | 5.00E+05/00 | 5.00E+05/00 |
| f6 | 1.92E+04/50 | 1.34E+04/50 | 1.04E+04/50 | 2.69E+04/44 | 2.69E+04/46 | 1.61E+04/50 |
| f7 | 3.00E+05/00 | 3.00E+05/00 | 3.00E+05/00 | 2.93E+05/05 | 3.43E+05/08 | 3.00E+05/00 |
| f8 | 6.44E+04/49 | 2.69E+05/06 | 8.93E+04/40 | 1.24E+05/32 | 2.47E+05/45 | 6.25E+04/47 |
| f9 | 1.79E+05/47 | 2.92E+05/02 | 2.00E+05/20 | 6.46E+04/45 | 7.52E+04/47 | 7.33E+04/48 |
| f10 | 9.70E+05/50 | 6.60E+04/50 | 1.27E+05/11 | 3.46E+04/50 | 8.39E+04/50 | 8.15E+04/50 |
| f11 | 8.98E+04/50 | 6.88E+04/45 | 9.53E+04/24 | 4.92E+04/42 | 5.73E+04/47 | 7.47E+04/50 |
| f12 | 5.12E+04/50 | 3.43E+04/50 | 6.78E+04/32 | 3.35E+04/44 | 3.35E+04/35 | 3.95E+04/50 |
| f13 | 6.37E+04/50 | 5.21E+04/46 | 1.28E+05/09 | 1.10E+05/19 | 1.28E+05/22 | 4.54E+04/50 |
表 4给出DE -BMS、DE/rand/1、DE/best/ 1、jDE、SaDE、EPSDE、文献[9]等7个算法在终止条件下获得的最优目标函数值的50次平均值(AVER)。实验的终止条件是适应度评价次数达到最大评价次数,其参数设置见表 1。
| 函数 | DE/rand/1 | DE/best/1 | SaDE | jDE | EPSDE | 文献[9] | DE⁃BMS |
| f1 | 2.86E-44 | 6.46E-67 | 1.33E-99 | 6.86E-131 | 7.61E-108 | 5.37E-95 | 1.80E-58 |
| f2 | 1.05E-27 | 4.75E-40 | 3.73E-70 | 3.37E-80 | 2.56E-68 | 3.45E-86 | 1.75E-32 |
| f3 | 3.94E+03 | 8.38E+02 | 5.46E-11 | 3.22E-24 | 4.32E-19 | 5.47E-08 | 6.76E+02 |
| f4 | 5.63E-12 | 1.59E-23 | 1.24E-06 | 1.93E+01 | 2.73E-04 | 3.48E-10 | 3.19E-13 |
| f5 | 2.50E+01 | 2.39E+01 | 1.49E+01 | 8.77E-01 | 5.68E+00 | 4.58E+01 | 2.46E+01 |
| f6 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 8.80E-01 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| f7 | 6.61E-03 | 4.12E-03 | 4.40E-03 | 2.12E-03 | 2.22E-03 | 5.52E-03 | 6.47E-03 |
| f8 | -3.64E-12 | 2.77E+02 | 2.13E+01 | 7.11E+01 | 3.41E+01 | 5.34E+01 | 2.37E+00 |
| f9 | 3.98E-02 | 5.35E+00 | 8.56E-01 | 1.99E-01 | 2.64E-01 | 3.25E-01 | 1.99E-02 |
| f10 | 7.11E-15 | 6.75E-15 | 8.56E-01 | 1.86E-02 | 2.68E-12 | 3.48E-13 | 7.11E-15 |
| f11 | 0.00E+00 | 1.33E-03 | 1.93E-02 | 1.63E-03 | 1.45E-03 | 1.82E-03 | 0.00E+00 |
| f12 | 3.40E-32 | 1.57E-32 | 1.45E-02 | 1.04E-02 | 1.57E-32 | 1.57E-32 | 1.57E-32 |
| f13 | 3.19E-29 | 8.68E-01 | 1.27E+01 | 8.20E+00 | 6.35E+00 | 1.35E-32 | 1.35E-32 |
| 注:表中的数字加粗表示在该行对应函数下只有该列所对应的算法获取的解是最佳的 | |||||||
从表 4可以看出,DE/rand/1在f6和f11两个函数上的性能最好,DE/best/1在f4、f6、f10和f12 4个函数上的性能最好,jDE在f1、f2、f3和f5 4个函数上的性能最好,SaDE仅在f6上性能最好;比之下,DE- BMS算法在f6、f8、f9、f11、f12和f13 6个函数上性能最好。这说明DE- BMS算法在解质量方面优于其他4个算法,特别是在优化多峰函数问题时表现更佳。
3 结语本文借助于动态集成的基本思想给出了一种改进的差分进化算法,从策略库中依据选择概率动态选取变异策略。该算法既充分利用多个策略的优势,又使得算法简单易执行。通过使用适应度平均次数、成功运行次数和解质量三种评价指标,与其他算法在13个测试函数上的运算比较验证了DE-BMS算法在求解带约束的多峰优化问题方面有一定的优势。
正如“没有免费的午餐”,没有任何一种算法在所有的问题上都有优势,虽然本文算法在求解多峰优化问题上具有一定的优势,且动态计算开销比较低,但是对多目标优化问题和其应用仍需要进一步的深入研究。
| [1] |
STORN R, PRICE K. Differential evolution: A simple and efficient adaptive scheme for global optimization over continuous spaces[DB/OL].[2018-10-10]. https://www.docin.com/p-618547768.html.
|
| [2] |
STORN R, PRICE K, LAMPINEN J. Differential Evolution:A Practical Approach to Global Optimization[M]. New York: Springer Verlag, 2005.
|
| [3] |
汪慎文, 丁立新, 张文生, 等. 差分进化算法研究进展[J]. 武汉大学学报(理学版), 2014, 60(4): 283-292. WANG S W, DING L X, ZHANG W S, et al. Survey of differential evolution[J]. Journal of Wuhan University (Natural Science Edition), 2014, 60(4): 283-292. (Ch). |
| [4] |
FAN H Y. A trigonometirc mutation operator to differential evolution[J]. Journal of Global Optimization, 2003, 27(1): 105-129. DOI:10.1023/A:1024653025686 |
| [5] |
WANG S W, DUAN Y M, SHU W N, et al. Differential evolution with elite mutation strategy[J]. Journal of Computational Information Systems, 2013, 9(3): 855-862. |
| [6] |
BREST J, GREINER S, BOSKOVIC B, et al. Selfadapting control parameters in differential evolution:A comparative study on numerical benchmark problems[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(6): 646-657. DOI:10.1109/tevc.2006.872133 |
| [7] |
LIU J H, LAMPINEN J. A fuzzy Adaptive differential evolution algorithm[J]. Soft Computing, 2005, 9(6): 448-462. DOI:10.1007/s00500-004-0363-x |
| [8] |
ZHANG J Q, SANDERSON A C. JADE:Adaptive differential evolution with optional external archive[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958. DOI:10.1109/TEVC.2009.2014613 |
| [9] |
ESSAID M, IDOUMGHAR L, LEPAGNOT J, et al. A Hybrid Differential Evolution Algorithm for Real World Problems[DB/OL].[2018-10-20]. https://www.re-searchgate.net/publication/326446144_A_Hybrid_Differ-ential_Evolution_Algorithm_for_Real_World_Problem. DOI: 10.1109/CEC.2018.8477965.
|
| [10] |
RAHNAMAYAN S, TIZHOOSH H, SALAMA M. Opposition -Based differential evolution[J]. IEEE Trans-actions on Evolutionary Computation, 2008, 12(1): 64-79. DOI:10.1109/TEVC.2007.894200 |
| [11] |
SUN J Y, ZHANG Q F, TSANG E P K. DE/EDA:A new evolutionary algorithm for global optimization[J]. Information Sciences, 2005, 169(3): 249-262. DOI:10.1016/j.ins.2004.06.009 |
| [12] |
LIU H, CAI Z X, WANG Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization[J]. Applied Soft Computing, 2010, 10(2): 629-640. DOI:10.1016/j.asoc.2009.08.031 |
| [13] |
MALLIPEDDI R, SUGANTHAN P, PAN Q, et al. Differential evolution algorithm with ensemble of parameters and mutation strategies[J]. Applied Soft Computing, 2011, 11(2): 1679-1696. DOI:10.1007/978-3-642-17563-3_9 |
| [14] |
QIN A K, HUANG V L, SUGANTHAN P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417. DOI:10.1109/TEVC.2008.927706 |
| [15] |
YAO X, LIU Y, LIU G M. Evolutionary programming made faster[J]. IEEE Transactions on Evolutionary Computation, 1999, 3(2): 82-102. DOI:10.1109/4235.771163 |
 2019, Vol. 65
2019, Vol. 65




