文章信息
- 曾辰子, 余旌胡, 邹桢苹
- ZENG Chenzi, YU Jinghu, ZOU Zhenping
- 基于多样变异随机搜索的差分进化算法
- Differential Evolution Algorithm Based on RandomSearch with Diversity Mutation
- 武汉大学学报(理学版), 2018, 64(3): 211-216
- Journal of Wuhan University(Natural Science Edition), 2018, 64(3): 211-216
- http://dx.doi.org/10.14188/j.1671-8836.2018.03.002
-
文章历史
- 收稿日期:2016-12-28

2. 武汉大学 经济与管理学院, 湖北 武汉 430072
2. School of Economics and Management, Wuhan University, Wuhan 430072, Hubei, China
差分进化算法(differential evolution, DE)是一种用于解决连续优化问题的群启发式随机搜索算法, 具有全局搜索能力强, 算法简单, 参数少, 易于实现等优点[1].但是, 和其他的群智能算法一样, DE算法也有受参数影响大, 易陷入局部最优, 开发能力不足等缺点[2], 此外, 不像精英遗传算法, DE算法是不依概率收敛的[3].
目前, 国内外学者针对上述问题的研究取得了不少成果.Qin等人[4]通过构建试验个体产生策略候选池提出经典的自适应差分进化算法(SaDE).Zhang等人[5]采用DE/current-to-pbest变异方法, 提出具有外部最优存档的DE算法(JADE);Mallipeddi等人[6]提出集成变异和参数自适应调整策略的DE算法(EP SDE).Li等人[7]利用高斯变异和多样逆转抽样提出依概率收敛的GRFDE算法;近期, 彭虎等人[8]构造了具有较快收敛速度的三角骨架DE算法(tBBDE), 并利用随机泛函理论证明tBBDE依概率收敛;此外, Hu等人[9]给出了具有开创意义的DE算法收敛到全局最优点充分条件并构建算法依概率收敛的框架模式.
为了避免DE算法陷入局部最优, 加强算法局部搜索能力, 提高收敛速度, 本文提出一种基于多样变异随机搜索的差分进化算法(DMSDE).DMSDE沿用基本DE算法的变异算子, 并采用变异比例因子自适应调整策略, 然后改进DE算法交叉算子, 最后, 在贪婪选择操作前设计了多样变异搜索算子.数值实验表明, DMSDE算法具有较好的优化性能.
1 差分进化算法差分进化算法(DE)是Storn和Price在1995年提出的基于实数编码的进化算法[9].对于如下的最小优化问题:
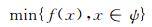
|
(1) |
这里ψ是D维非空有界闭集.算法首先在解空间内均匀随机产生N个初始个体形成初始种群X0={x10, x20, …,xN0}, 令t=0, 1, 2,…, 表示进化代数, 则在每一代算法按照如下步骤进行迭代, 直到满足所设定的终止条件.
Step 1(变异):对种群中每个个体xit, i=1, …, N, 通过下列方式产生对应的变异个体
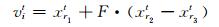
|
(2) |
其中, F是变异比例因子, 为(0, 1]间的常数, r1, r2, r3∈{1, 2, …,N}且r1≠r2≠r3≠i.
Step 2(交叉):将每个个体xit和它对应的变异个体vit进行二项交叉得到试验个体uit=(ui, 1t, …, ui, Dt), 方法为
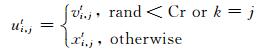
|
(3) |
其中, Cr是交叉比例因子, 为(0, 1]间的常数, rand~U[0, 1], k∈{1, …, D}是一个随机整数, 确保试验个体至少在某一维上取自变异个体中的对应元素.
Step 3(选择):通过如下方式取目标个体xit和它对应的试验个体uit中最好的个体保留到下一代
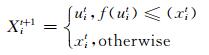
|
(4) |
DE算法的关键步骤是其差分变异操作, 使得种群具有较强的全局搜索能力, 然而一旦种群陷入局部最优, 变异算子的搜索能力会快速下降, 通过目标个体和对应变异个体进行交叉, 在贪婪选择条件下, 种群依然无法逃出局部最优.所以, 本文保留DE算法极具特性的变异操作, 受Gu等人[10]的启发,在进化的每一代, 对种群中每个个体xit和对应变异个体vit采用如下改进的交叉算子形成中间试验个体uit= (ui, 1t, …, ui, Dt):
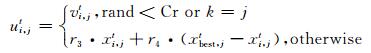
|
(5) |
其中,rand~U[0, 1], r3和r4是[0, 1]之间均匀分布随机数, 且满足r3+r4=1.xbest, jt是当前种群最好个体第j维分量.
在改进的交叉算子中, 由于r3和r4的随机性, 增加了种群多样性, 避免个体陷入局部最优;交叉过程中利用当前最好个体的信息, 提高了算法局部搜索能力, 有利于算法的快速收敛.
2.2 多样变异搜索算子为进一步提高算法的局部搜索能力并巩固算法的全局勘探能力, 在改进交叉算子后, 每个中间试验个体uit都以一个较小的概率m(这里m是一个控制参数)变异为从给定概率密度函数中随机抽取的一个样本, 否则保持不变, 从而形成试验个体wit, 具体表达式如下:
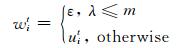
|
(6) |
其中,λ~U[0, 1], 理论上ε是按概率密度函数
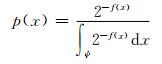
|
在解空间中产生的随机个体.由于常用的计算软件可从非标准的概率密度函数中抽取满足条件的样本, 在实际中以非标准概率密度函数F进行操作.
从所构造的概率密度函数来看, 随机抽取的个体更偏向于落在具有较小适应值个体的附近, 那么, 当λ≤m时,所得到的个体在解空间中会有大的概率在好的区域进行搜索.这个新颖的多样变异搜索算子使得个体进行更有针对性的变异, 加强了算法的局部搜索能力, 同时个体能够变异到解空间中的任意位置, 确保了种群多样性.
2.3 变异比例因子F和交叉比例因子Cr的调整在DE算法中, 变异比例因子F和交叉比例因子Cr对算法的全局搜索能力和收敛速度有着重要影响[11].根据一些研究者对这两个经验参数的研究, 在DE算法中, F=0.5, Cr=0.9是一个较好的选择[12, 13].基于此, 本文在将要提出的DMSDE算法中, Cr沿用DE算法中的0.9, F采用如下公式进行自适应调整:
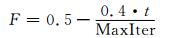
|
(7) |
其中,t为当前迭代数, MaxIter是最大迭代次数, 那么F的取值范围为[0.1, 0.5].事实上, 在迭代搜索的前期, 较大的F会增强算法的全局搜索能力, 在后期小的F有利于算法收敛.
2.4 DMSDE算法框架从避免算法陷入局部最优并提高收敛速度的角度, 本文在DE算法的基础上改进了其交叉操作, 并加入一个新颖的多样变异算子, 同时采用变异比例因子F的自适应调整策略, 提出一种基于多样变异随机搜索的差分进化算法(DMSDE), 具体描述见算法1.
| 算法1 DMSDE算法 |
| 输入:种群大小N, 个体维数D, 交叉比例因子Cr, m. |
| 输出:全局最优解. |
| Step 1:在解空间中均匀随机产生N个D维个体, 形成初始种群, 迭代次数t置为0. |
| Step 2:评价初始种群的适应函数值. |
| Step 3: Whilet < MaxIter |
| 根据(7)式对变异比例因子F进行更新 |
| For i=1:N |
| 由(2)式和(5)式的变异算子与改进的交叉算子得到中间试验个体uit.根据多样变异搜索算子中的(6)式得到试验向量wit. |
| 评价试验向量wit的适应函数值. |
| 由(4)式通过贪婪选择产生下一代相应个体; |
| End for |
| t=t+1; |
| End While |
一般而言,理论上确保收敛的算法具有较高的稳健性和更强的跳出局部最优的能力.Hu等人[9]给出了改进DE算法能够依概率收敛的充分条件, 本文将基于此充分条件对DMSDE算法的收敛性进行分析.
考虑到实际问题中解的精度, 不失一般性, 令Sδ*={x||f(x*)-f(x)| < δ}表示扩大的全局最优解集合, δ为求解精度, x*是全局最优点.下面给出算法依概率收敛的定义以及DE算法依概率收敛的充分条件.
定义1[14] 种群序列{Xt, t=0, 1, …}依概率收敛到Sδ*, 当且仅当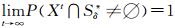
引理1[14] 采用贪婪选择策略的改进DE算法求解优化问题((1)式)时依概率收敛, 若存在单调递增序列{tk; k≥1}⊂{1, 2, …}及非负序列{ξ(tk); k≥1}使得算法在第tk代目标种群中, 至少存在一个个体, 通过繁殖算子产生的对应试验个体y满足P(y∈Sδ*)≥ξ(tk)>0且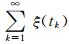
定理1 DMSDE算法是依概率全局收敛的.
证 从两个方面分析DMSDE算法的特征.
1) DMSDE能保留当前种群中的最优解到下一代.
DMSDE算法的选择操作算子保留了DE算法的贪婪选择策略, 所以种群中的最优个体可以保留到下一代.
2) 在DMSDE的繁殖算子(变异算子, 改进的交叉算子和多样变异算子)作用下, 每代种群中的试验个体进入全局最优解集合Sδ*的概率足够大.
事实上, 试验个体y进入全局最优解集合Sδ*的概率P(y∈Sδ*), 不小于单独由多样变异算子中p(x)产生的个体进入Sδ*的概率, 即
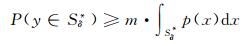
|
那么对于具有N个个体的种群, 由多样变异算子中p(x)产生的新个体都不进入Sδ*的概率
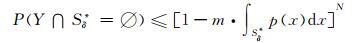
|
这里Y表示试验个体所组成的试验种群.则单独由p(x)产生的试验个体中至少有一个进入Sδ*的概率
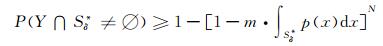
|
令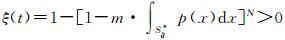
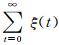
事实上, 从定理1证明过程可以发现, ξ(t)为一常数, 其值越大, 算法以较快的速度收敛于全局最优解集合的概率就越大, 这给本文所提出的DMSDE算法提供了理论依据, 在不打破算法求全与求精能力的平衡性时, 可以适当提高m的值来加快算法的收敛速度.这也是未来一个改进方向.
4 实验与分析实验利用Matlab R2014a编程实现, 本文选取8个常用的标准测试函数(30维), 函数的具体情况见表 1.实验中, DMSDE算法种群大小N=50, Cr=0.9,m=0.1, 参与比较的算法包括DE算法DE/rand/1/bin, 3个国际知名改进算法SaDE, EPSDE, JADE, 最近提出的具有较快收敛速度且依概率收敛的算法tBBDE[8], 这些比较算法种群大小统一为N=100, 其他关键参数与原文献相同, 各算法终止条件为达到设定的最大迭代次数.
| 类型 | 函数 | 函数名 | f(x*) | 范围 |
| 单峰函数 | f1 | Sphere | 0 | [-100, 100] |
| f2 | Schwefel 2.22 | 0 | [-10, 10] | |
| f3 | Schwefel 1.2 | 0 | [-100, 100] | |
| f4 | Schwefel 2.21 | 0 | [-100, 100] | |
| 多峰函数 | f5 | Rosenbrock | 0 | [-30, 30] |
| f6 | Rastrigin | 0 | [-5.12, 5.12] | |
| f7 | Ackley | 0 | [-32, 32] | |
| f8 | Griewank | 0 | [-600, 600] |
表 2分别给出了6种算法在标准测试函数上独立运行30次得到的结果, Mean为30次所求得最优解的平均值, Std为标准差.对表 2进行分析可以发现, 在单峰函数上DMSDE算法能获得更好的解, 优势明显, 说明算法具有较强的寻优能力和较高的收敛精度.在多峰问题上, 其中对f6~f8, DMSDE算法都能找到算法的全局最优点, 特别在优化f6和f7时, 打败了其他竞争算法, 收敛精度比其他算法高出很多, 表明DMSDE算法跳出局部最优的能力较强, 收敛速度较快.虽然它在f5上没有获得更好的解, 但是它比依概率收敛的tBBDE算法得到的最优解要好, 并且在所有的测试函数中DMSDE算法的稳定性是最好的, 具有较好的鲁棒性.
| 函数 | 迭代次数 | 指标 | DE/rand/1/bin | JADE | SaDE | EPSDE | tBBDE | DMSDE |
| f1 | 1 000 | Mean Std |
6.29E-09 3.84E-09 |
2.18E-37 8.08E-38 |
2.09E-24 2.21E-24 |
1.95E-26 8.99E-26 |
2.56E-30 4.40E-30 |
1.19E-39 1.35E-39 |
| f2 | 1 000 | Mean Std |
7.41E-05 1.85E-05 |
1.74E-18 5.15E-19 |
3.94E-13 1.85E-13 |
1.75E-10 2.24E-10 |
1.38E-20 1.02E-20 |
5.90E-22 4.24E-22 |
| f3 | 1 000 | Mean Std |
2.69E+01 1.40E+01 |
1.04E-01 4.51E-02 |
3.06E-04 6.74E-04 |
3.67E+00 1.91E+01 |
3.34E+02 2.21E+02 |
2.42E-09 5.52E-09 |
| f4 | 1 000 | Mean Std |
3.35E-01 5.18E-01 |
4.03E-08 1.67E-08 |
3.49E-04 2.73E-04 |
1.39E-01 1.81E-01 |
1.60E-03 8.41E-04 |
3.63E-14 2.91E-14 |
| f5 | 1 500 | Mean Std |
1.69E+01 1.30E+00 |
1.35E+01 7.19E+00 |
7.02E+00 1.50E+00 |
3.01E-01 7.97E-01 |
4.51E+01 3.03E+01 |
2.79E+01 3.82E-01 |
| f6 | 1 500 | Mean Std |
1.74E+02 1.29E+01 |
7.06E+01 7.18E+00 |
2.55E-12 6.59E-12 |
3.93E-09 2.08E-08 |
7.56E+00 2.35E+00 |
0.00E+00 0.00E+00 |
| f7 | 1 500 | Mean Std |
1.39E-08 4.57E-09 |
4.26E-15 1.45E-15 |
3.55E-15 0.00E+00 |
3.67E-15 6.49E-16 |
6.28E-15 1.53E-15 |
0.00E+00 0.00E+00 |
| f8 | 1 500 | Mean Std |
3.29E-04 1.80E-03 |
0.00E+00 0.00E+00 |
9.85E-04 3.80E-03 |
4.93E-04 1.90E-03 |
3.10E-03 6.60E-03 |
0.00E+00 0.00E+00 |
| 注:黑体数字表示为最优结果 | ||||||||
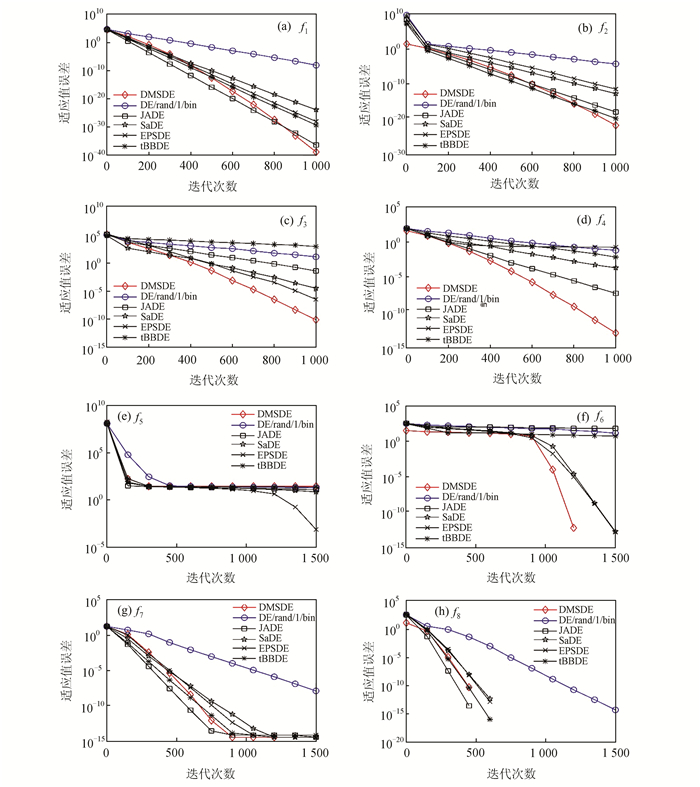
为了更直观的分析DMSDE算法的优化效果, 图 1给出了6种算法分别在8个测试函数上的收敛曲线图.从图 1可以看出, 在单峰函数上, 迭代搜索的前期算法具有较高的全局搜索能力, 在后期算法收敛速度明显加快.在多峰函数上, 除了f5,在f6, f7, f8上都好于或与其他算法相当, 特别是和DE算法相比,DMSDE算法无论是在收敛速度还是收敛精度方面都有了极大的提高.
|
| 图 1 各算法在8个函数上的收敛曲线图 Figure 1 The convergence curve of each algorithm on eight functions |
本文提出一种基于多样变异随机搜索的差分进化算法(DMSDE), 在保留DE算法变异操作条件下, 改进其交叉算子, 避免种群陷入局部最优, 加快算法收敛, 其后采用一个新颖的多样变异算子, 增强算法局部开发能力并巩固其全局勘探能力.在8个标准测试函数上进行试验, 与DE/rand/1/bin, SaDE, EPSDE, JADE, tBBDE算法相比, 验证了本文所提算法在整体上具有较高的求解精度和稳健性, 以及较快的收敛速度, 符合理论上的预期.将来的研究工作会将多样变异算子的基本思想应用于其他群智能算法并解决相关实际问题.
| [1] |
STORN R, PRICE K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.4236/ti.2013.41B012 |
| [2] |
ALI M, PANT M. Improving the performance of differential evolution algorithm using Cauchy mutation[J]. Soft Computing, 2011, 15(5): 991-1007. DOI:10.1007/s00500-010-0655-2 |
| [3] |
李敏强, 寇纪淞, 林丹, 等. 遗传算法的基本理论与应用[M]. 北京: 科学出版社, 2002: 75-94. LI M Q, KOU J S, LIN D, et al. Basic Theory and Application of Genetic Algorithm[M]. Beijing: Science Press, 2002: 75-94. |
| [4] |
QIN A K, HUANG V L, SUGANTHANP N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417. DOI:10.1109/TEVC.2008.927706 |
| [5] |
ZHANG J, SANDERSON A C. JADE: Adaptive differential evolution with optional external archive[J]. Evolutionary Computation IEEE Transactions on, 2009, 13(5): 945-958. DOI:10.1109/TEVC.2009.2014613 |
| [6] |
MALLIPEDDI R, SUGANTHAN P N, PAN Q K, et al. Differential evolution algorithm with ensemble of parameters and mutation strategies[J]. Applied Soft Computing, 2011, 11(2): 1679-1696. DOI:10.1016/j.asoc.2010.04.024 |
| [7] |
LI D, CHEN J, XIN B. A novel Differential Evolution algorithm with Gaussian mutation that balances exploration and exploitation[C]//2013 IEEE Symposium on Differential Evolution (SDE). New York: IEEE Press, 2013: 18-24. DOI: 10.1109/SDE.2013.6601437.
|
| [8] |
彭虎, 吴志健, 周新宇, 等. 基于三角的骨架差分进化算法[J]. 计算机研究与发展, 2015, 52(12): 2776-2788. PENG H, WU Z J, ZHOU X Y, et al. Bare-bones differential evolution algorithm based on trigonometry[J]. Journal of Computer Research and Development, 2015, 52(12): 2776-2788. DOI:10.7544/issn1000-1239.2015.20140230 |
| [9] |
HU Z B, XIONG S W, SUQ H, et al. Sufficient conditions for global convergence of differential evolution algorithm[J]. Journal of Applied Mathematics, 2013, 2013(5): 1044-1065. DOI:10.1155/2013/193196 |
| [10] |
GU J R, GU G J. Differential Evolution with a local search operator[C]//Informatics in Control, Automation and Robotics (CAR), 2010 2nd International Asia Conference on. New York: IEEE Press. 2010: 480- 483. DOI: 10.1109/CAR.2010.5456601.
|
| [11] |
CAI Y Q, WANG J H. Differential evolution with neighborhood and direction information for numerical optimization[J]. IEEE Transactions on Cybernetics, 2013, 43(6): 2202-2215. DOI:10.1109/TCYB.2013.2245501 |
| [12] |
HU Z B, XIONG S W, SU Q H, et al. Finite Markov chain analysis of classical differential evolution algorithm[J]. Journal of Computational & Applied Mathematics, 2014, 268(1): 121-134. DOI:10.1016/j.cam.2014.02.034 |
| [13] |
WANG H, RAHNAMAYAN S, SUN H, et al. Gaussian bare-bones differential evolution[J]. IEEE Transactions on Cybernetics, 2013, 43(2): 634-647. DOI:10.1109/TSMCB.2012.2213808 |
| [14] |
胡中波. 依概率收敛差分演化算法的理论与算法设计[D]. 武汉: 武汉理工大学, 2014. HU Z B. The Theoretical Researches and Algorithmic Design of Convergent Differential Evolution Algorithm in Probability [D]. Wuhan: Wuhan University of Technology, 2014(Ch). http://cdmd.cnki.com.cn/Article/CDMD-10497-1015001572.htm |
 2018, Vol. 64
2018, Vol. 64





