文章信息
- 甘海慧, 熊俊俏, 陈爱杰, 曹新莉
- GAN Haihui, XIONG Junqiao, CHEN Aijie, CAO Xinli
- 基于子载波快跳频的短波BICM-OFDM/FH系统
- A Short-Wave BICM-OFDM/FH System Based on Subcarrier Fast Frequency Hopping
- 武汉大学学报(理学版), 2016, 62(6): 547-551
- Journal of Wuhan University(Natural Science Edition), 2016, 62(6): 547-551
- http://dx.doi.org/10.14188/j.1671-8836.2016.06.010
-
文章历史
- 收稿日期:2016-03-20

2. 武汉工程大学 电气信息学院,湖北 武汉 430205
2. School of Electrical and Information Engineering, Wuhan Institute of Technology, Wuhan 430205, Hubei, China
在短波跳频系统中,当正交频分复用(OFDM)符号的循环前缀的长度达不到信道最大时延长度时,仍存在多径干扰,信道呈现频率选择性衰落.为了抵抗多径干扰和频率选择性衰落,前人提出了各种分集方法的应用,如子载波扩频(MC-CDMA)[1]、子带重发(MB-OFDM)[2]、预编码[3, 4]与子载波快跳频的正交频分复用(FFH-OFDM)技术[5, 6]实现频率分集.从频带带宽考虑,子载波快速跳频所占用的带宽窄,解调简单.文献[7]提出的比特交织编码调制-正交频分复用(BICM-OFDM)方法,以时间分集的方式抵抗频率选择性衰落,提高了系统的性能.文献[8]将BICM技术应用于短波差分跳频系统,并取得了明显的效果.
针对短波时变色散衰落信道,为了兼顾短波跳频通信系统的跳频速率与OFDM调制符号的完整性,同时,由于OFDM符号的循环前缀的长度并不能达到短波最大时延长度,本文将BICM-OFDM应用于短波子载波快速跳频系统中,以进一步改善短波跳频通信的性能,并对其进行了理论分析和数值仿真.
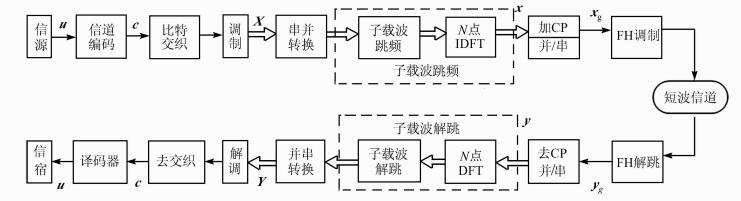
1 本文的跳频系统结构信源产生的信息比特序列u经过信道编码后,便得到码元序列ci={u, cp},其编码比特数为M·N.连续的编码序列{ci}按列交织,每相邻的M列码元(ci, ci+N, …, ci+(M-1)N)映射为一个调制符号,设符号序列集X={X0, X1, …, XN-1}.该符号序列集经过串/并转换为N路符号并行输出,每个符号对应一个子载波(OFDM符号的子载波数为N),获得BICM-OFDM调制,如图 1所示.
|
| 图 1 基于BICM的OFDM-FH系统结构流程图 Figure 1 System structure diagram of OFDM-FH system based on BICM |
显然,连续的编码比特被映射到不同的调制符号内,经过不同的子载波传输,而相邻的M·N个编码数据处于一个OFDM符号内,经过载波跳频传输.由于信号带宽远大于信道的相干带宽,因此,各子载波呈现彼此独立的频率选择性瑞利衰落.
为获得带内频率分集以及更好的信道估计,在每个BICM-OFDM符号周期内,将发送数据轮流在每个子载波上发送,构成带内快跳频(FFH),N个子载波通过N点IDFT调制,便得到时域信号X={X0, X1, …, XN-1}T.为了将数据在不同的子载波上传输,且保持子载波的正交性,最简单的方式是调整逆傅立叶变换系数的位置,得到其子载波快跳频矩阵[4, 9, 10]

|
(1) |
式中:μ, ν=1, 2, …, N.显然,当μ为零时,则为常规的OFDM.
当通过傅立叶逆变换,则可得到FFH-OFDM符号为
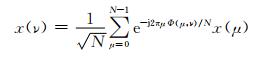
|
(2) |
简记为
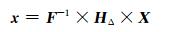
|
(3) |
式中:F-1为傅立叶逆变换矩阵,HΔ为子载波快跳频模型(即预编码矩阵).
将OFDM符号按照跳频图案映射到相应的射频频率上,以跳频信号的形式发射至短波信道上.其跳频信号通过信道进入接收端后先经过载波解跳处理,将射频信号转换为基带信号yg,然后去循环前缀,再经过N点DFT解调和子载波解跳处理,便得到频域信号Y,即
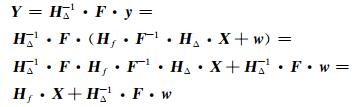
|
(4) |
上式中:Hf为短波信道响应函数,是对角矩阵,即Hf=diag (α1, α2, …, αN);w为零均值的信道高斯白噪声.
2 比特误码性能分析FFH-OFDM符号调制为正交相移键控(QPSK)调制,根据(4)式,当系统完全同步,且已知信道状态信息(CSI)条件下,则接收信号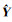
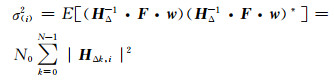
|
(5) |
第i个子信道输出信号的信噪比为
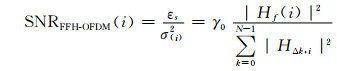
|
(6) |
式中:
整个FFH-OFDM接收符号的平均信噪比为[11]
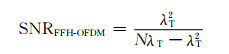
|
(7) |
式中λT为
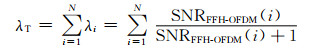
|
显然:通过子载波内的快跳频进行频率分集,便可以有效地改善子信道的信噪比.
此时,QPSK调制时所对应的FFH-OFDM符号平均差错率为
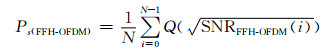
|
(8) |
下面分析BICM与卷积编码技术相结合时,对其系统比特误码率性能的改善.对于接收信号Yn,当已知信道信息(CSI)的情况下,根据最大似然(ML)准则进行译码判决[12].
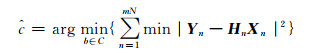
|
(9) |
式中:c为二进制码集,Xn为发送的信号,Yn为对应的接收信号,m为每个调制符号所包含的码元数,即码元(ci, ci+N, …, ci+(m-1)N)所对应的信号为Xn(n=1, 2, …, N).
相应的比特误码率的上限为[13]
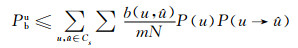
|
(10) |
式中:u为发送码字, 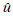
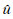
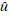
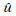
若假设只有一个比特错误,则可得到比特误码率的下限为
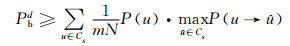
|
(11) |
显然,比特误码率限的关键是成对错误概率P(u→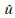
令发送u与接收判决的码字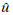
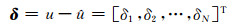
|
(12) |
则由于高斯信道衰落因子αk引起的成对错误概率[14]为
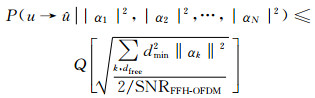
|
(13) |
式中:dmin为两个符号的最小欧氏距离.
进一步采用高斯概率积分的替代表示,可得到在子载波信道衰落统计独立条件下的平均成对错误概率上限为
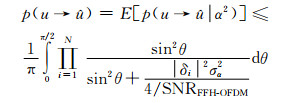
|
(14) |
式中:σα2为子载波信道的随机幅度衰落因子{αk}的方差, θ为高斯积分变量.
3 数值仿真的结果与分析为了说明BICM对OFDM/FH系统性能的影响,下面将对其进行数值仿真与性能分析.
3.1 仿真条件本文的系统采用宽间隔跳频以克服多径影响,其系统的跳频速率为200 kb/s,编码方式为卷积码,子生成元为(133, 171)8,自由距离dfree=10.经过删余处理,码率为3/4,BICM调制采用Gray码符号映射,调制方式为QPSK.OFDM符号周期为5 ms,其中信息Ts=4 ms,循环前缀Tg=1 ms,子载波频率间隔250 Hz.OFDM采用64路子载波,其中1/4的子载波作为导频,用于同步和信道估计,各子载波所对应的信号带宽分别为16 kHz,其数据速率分别为14.4 kb/s,均能满足短波交互式话音通信和数据通信的要求.最后利用解调、去交织和译码,即可以从频域信号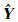
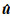
为了分析BICM和FFH技术对OFDM系统性能改善的效果,采用Monte-Carlo方法进行数值仿真,其中码字的检测采用维特比判决译码,并假设系统同步,且完全已知信道状态信息(CSI).
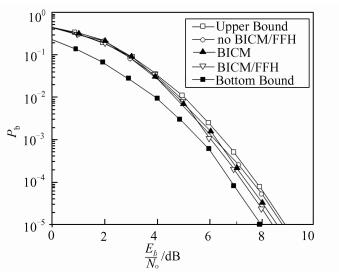
针对短波OFDM/FH系统,首先研究BICM技术、FFH技术在加性高斯白噪声(additive white gaussian noise, AWGN)信道条件下的比特误码率Pb,其数值仿真结果如图 2所示.其中,比特误码率的上限和下限曲线可由(10)式和(11)式直接获得,而系统采用BICM和FFH技术的比特误码率曲线用Monte-Carlo方法进行数值仿真获得.
|
| 图 2 AWGN信道条件下,系统的Pb与Eb/No关系曲线 Figure 2 The relationship between Pb and Eb/No, under AWGN channel |
从图 2中可见:在加性高斯白噪声信道条件下,Pb为1.0×10-5时,采用BICM技术可以获得约0.5 dB的编码增益.在BICM技术的基础上,采用子载波快跳频技术,其系统比特误码率性能改善程度并不大,且在信噪比小于5.3 dB时,子载波FFH技术使系统的比特误码性能恶化, 这种现象与文献[16]的结论是完全一致的.
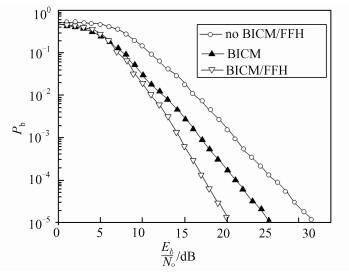
针对短波时延信道,这里考虑3条路径的情形,每条路径的幅度衰落系数、相移(°)、时延(ms)和多普勒频移(Hz)参数分别对应为(0.36, 249.6, 0.8, -0.06)、(0.50, 86.5, 1.5, -1.18)和(1.00,83.4, 2.4,-0.69)[17].在短波多径衰落信道条件下,子载波数为64时,系统的比特误码率数值仿真结果如图 3所示.
|
| 图 3 短波多径衰落信道条件下,系统的Pb与Eb/No关系曲线 Figure 3 The relationship between Pb and Eb/No, under shortwave multipath fading channels |
从图 3中可见:BICM和FFH技术的结合可以有效地提高系统抗频率选择性衰落的影响.在短波多径衰落信道中,以64个子载波为例,当Pb为1.0×10-5时,采用BICM技术会使编码增益达到5 dB;若同时采用BICM和FFH技术,编码增益将达到10 dB.同时还可见:在低信噪比时(小于5.3 dB),子载波FFH技术会使其系统的性能恶化;只有在高信噪比时,子载波快跳频技术才能改善系统的性能;与高斯信道不同,子载波数量增加时,比特误码率性能有所下降.
与文献[4, 5, 9, 11, 18]相比,本文结合BICM技术的数值仿真结果明显优于单纯的FFH-OFDM技术;与文献[7, 8, 15]相比,由于子载波快跳频,其数值仿真结果优于单纯的BICM-OFDM.
4 结论在OFDM/FH系统中,由于子载波快跳频能有效克服部分延时较大的多径信号,因此改善了信号传输的条件.本文所提出的综合应用BICM和子载波间的快跳频FFH技术,通过上述的理论分析与数值仿真表明:1)在高斯白噪声信道条件下,子载波快跳频技术并不能获取额外的系统增益,在信噪比小于5.3 dB时,子载波快跳频反而会使系统比特误码率性能恶化;2)在加性高斯白噪声信道条件下,采用BICM与子载波快跳频相结合的技术并不能获取高的系统增益,当比特误码率为1.0×10-5时,可获得0.5 dB的编码增益,这主要是因为在高斯信道条件下,无论快跳频或BICM技术,对系统性能改善的效果有限;3)针对衰落信道条件,BICM技术均能较大地改善系统的比特误码率性能,如当比特误码率Pb为1.0×10-5时,BICM技术会使编码增益达到5 dB;4) BICM与子载波快跳频技术相结合可显著地改善频率选择性衰落,当比特误码率为1.0×10-5时,其编码增益达到10 dB.由此可见,在短波信道中引入BICM技术和子载波的快跳频FFH技术,可有效提高OFDM/FH系统的比特误码率性能.同时,采用BICM和多载波FH相结合的技术并不会使系统的复杂度增加及产生处理延迟.显然,采用该技术的OFDM/FH系统是完全满足短波跳频实时话音通信的需求.
| [1] | MARCZAK A. Performance analysis of data transmission in MC-CDMA radio interface with turbo codes[J]. Telecommunication Systems , 2015, 59 (4) : 501–507 DOI:10.1007/s11235-014-9910-7 |
| [2] | KONDOJU S K, MANI V V, BOSE R, et al. Exact BER analysis of DCM for multiband OFDM-UWB system over uncorrelated Nakagami-m fading channels[C]//2014IEEE International Conference on Ultra-Wideband. New York: IEEE Press, 2014:473-478. |
| [3] | SUNAGA N, OHNO K, ITAMI M, et al. A theoretical study on demodulation of pre-coded OFDM by pre-coded symbol replacement[C]// 2012 International Symposium on Information Theory and its Applications. New York: IEEE Press, 2012:140-144. |
| [4] | JWA J W. An OFDM scheme with Pre-IDFT/DFT on frequency-selective Rayleigh fading channels[J]. IEICE transactions on Communications , 2005, 88 (7) : 3073–3077 |
| [5] | BERENS F, RUEGG A, SCHOLAND T, et al. Fast frequency hopping diversity scheme for OFDM-based UWB systems[J]. Electronics Letters , 2007, 43 (1) : 41–42 DOI:10.1049/el:20073776 |
| [6] | KUN X, YI X X. Parallel detection algorithm for fast frequency hopping OFDM[J]. Frequenz , 2011, 65 (3-4) : 87–91 |
| [7] | AKAY E, AYANOGLU E. Achieving full frequency and space diversity in wireless systems via BICM, OFDM, STBC, and viterbi decoding[J]. IEEE Transactions on communications , 2006, 54 (12) : 2164–2172 DOI:10.1109/TCOMM.2006.885089 |
| [8] | 朱毅超, 甘良才, 熊俊俏, 等. BICM在差分跳频系统中的应用[J]. 电波科学学报 , 2009, 24 (1) : 15–21 ZHU Y C, GAN L C, XIONG J Q, et al. Performance of BICM in the differential frequency hopping system[J]. Chinese Journal of Radio Science , 2009, 24 (1) : 15–21 |
| [9] | OTURAK A, ZTVRK E. Semi-analytical performance analysis of FFH-OFDM with MMSE receiver[C]//2014 22nd Signal Processing and Communications Applications Conference, New York: IEEE Press, 2014:1666-1669. |
| [10] | TARASAK P, LIN Z, PENG X, et al. Performance evaluation of fast frequency hopping OFDM over UWB channels[C]//Vehicular Technology Conference. New York: IEEE Press, 2009:1-5. |
| [11] | KWON H J, CHO J Y, CHO Y O, et al. Adaptive Data Multiplexing Method in OFDMA System and Transmission/reception Apparatus Thereof : US Patent, 20070064664 [P]. 2007-03-22. |
| [12] | WACHSMANN U, FISCHER R F H, HUBER J B, et al. Multilevel codes: Theoretical concepts and practical design rules[J]. IEEE Transactions on Information Theory , 2012, 45 (5) : 1361–1391 |
| [13] | BURY A, EGLE J. Diversity comparison of spreading transforms for multicarrier spread spectrum transmission[J]. IEEE Transactions on communications , 2003, 51 (5) : 774–781 DOI:10.1109/TCOMM.2003.811406 |
| [14] | SIMON M K, DIVSALAR D. Some new twists to problems involving the Gaussian probability integral[J]. IEEE Transactions on Communications , 1998, 46 (2) : 200–210 DOI:10.1109/26.659479 |
| [15] | YEH P C, ZUMMO S A, STARK W E, et al. Error probability of Bit-Interleaved coded modulation in wireless environments[J]. IEEE Transactions on Vehicular technology , 2006, 55 (2) : 722–728 DOI:10.1109/TVT.2005.863340 |
| [16] | 钱璟, 张申如. FFH-OFDM误码率性能的分析与仿真[C]//第十二届全国青年通信学术会议论文集.北京:电子工业出版社, 2007, 12 :1436-1440. QIAN J, ZHANG S R. BEF Performance Analysis & Simulation of FFH-OFDM[C]//12th session of the National Youth Communication Conference Proceedings.Beijing: Electronics Industry Press, 2007, 12 :1436-1440(Ch). |
| [17] | ZOU Z H. Implementation of short wave wideband data transmission by means of OFDM[C]//Environmental Electromagnetics. New York: IEEE Press, 2003:51-55. |
| [18] | GENG F Q, HUANG Z G, NING X J, et al. A joint improved irregular accumulate concatenated tree coding and frequency hopping OFDM modulation scheme for wireless networks[C]// Advanced Materials Research. Switzerland: Trans Tech Publications, 2014, 902 :364-369. |
 2016, Vol. 62
2016, Vol. 62




