文章信息
- 高志强, 崔翛龙, 杨伟锋, 周沙, 王昭
- GAO Zhiqiang, CUI Xiaolong, YANG Weifeng, ZHOU Sha, WANG Zhao
- 基于粒子群优化的差分隐私拟合框架
- Framework of Model Fitting under PSO-Guided Differential Privacy
- 武汉大学学报(理学版), 2019, 65(2): 213-217
- Journal of Wuhan University(Natural Science Edition), 2019, 65(2): 213-217
- http://dx.doi.org/10.14188/j.1671-8836.2019.02.011
-
文章历史
- 收稿日期:2018-09-08

2. 军委联参 55 所, 北京 100036;
3. 光大银行, 陕西 西安 710000
2. The 55th Institute of the Central Military Commission, Beijing 100036, China;
3. Everbright Bank, Xi'an 710000, Shaanxi, China
新科技革命的三驾马车“数据、算法、算力”不断推动着大数据、人工智能、移动互联网等技术的进步,同时,网购、移动支付、共享单车、无人驾驶等应用领域的突飞猛进,让用户切实感受到了新技术的便利,然而,Yahoo用户信息外泄、Facebook数据丑闻、Equifax大规模数据泄露等负面事件[1~3],还有生活中各种不停推送的“标签广告”,以及滴滴顺风车业务“乘客-司机”的标签争议[4~6],无时无刻不在提醒着我们,不可信第三方以收集个人数据形式提供的“便利”不是“免费的午餐”,利用机器学习将用户分类、打标签、做预测使得个人隐私成为“共享资源”,利益驱动下的数据滥用以及技术局限性造成隐私泄露已经成为备受关注并亟待解决的问题。
将敏感数据集完全暴露于不可信第三方和机器学习模型中,存在巨大的隐私泄露风险和安全隐患。基于差分隐私的敏感数据发布技术,具有强大的隐私保证和鲁棒性[5~9]。但传统差分隐私模型拟合方法存在缺陷:1)应用范围狭小,只局限于特定方法。文献[10]提出针对回归模型拟合的函数机制FM,虽然在线性回归问题效果很好,但在logistic回归上引入过多噪声扰动;文献[11]针对经验风险最小化问题提出一系列满足差分隐私的回归模型,但是正则因子消耗了大量隐私预算导致整体精度偏低。2)需要大量的随机扰动来满足差分隐私,导致模型性能差和复杂度高。文献[12]研究了差分隐私支持向量机的核函数,但其解决方案依旧是基于标准支持向量机模型,具有较高全局敏感度并引入大量噪声,针对大量数据的通用性和可用性有待提高。
本文提出满足差分隐私的监督学习模型拟合框架,在模型参数寻优过程中,引入满足差分隐私的粒子群优化算法,根据改进的指数机制,引导以参数向量形式编码的个体最优和群体最优粒子按照差分隐私的方式不断迭代学习。在每轮迭代中,依据粒子群优化算法的开采能力和快速全局收敛性能,不断修正个体最优和群体最优粒子向量,进而向全局最优方向进化。最终在保证机器学习模型可用性的同时,提高拟合框架对训练数据集的隐私保护性能。
1 预备知识 1.1 监督学习模型拟合问题监督学习的目标是利用数据和标签使算法模型具有学习能力,本质上,就是用拟合函数对数据集进行表征学习,直至收敛或达到预设阈值。下面给出机器学习[13]、监督学习模型拟合问题[14]的定义,以及回归[15]、支持向量机模型拟合[16]的预备知识。
定义1(机器学习)给定数据集X= {x1, x2, …, xn},构造从输入空间X到输出空间Y的函数映射f:X→Y,通过学习和优化策略得到机器学习的最优函数映射f,其中输入空间包含n个具有m类属性的数据样本xi={xi1, xi2, …, xim}。
定义2(监督学习模型拟合问题)给定具有n个元组的数据集D∈Γn,在回归、分类等经典监督学习模型中,其学习目标为利用拟合函数f(D, ω),通过调整参数ω来最佳拟合模型M与敏感数据集D,其中,最佳参数ω*对应最优拟合f(D, ω*)。
1)回归模型拟合
在线性回归模型中,给定数据集D= {(x1, y1), (x2, y2), …, (xm, ym)},其中,xi={xi1, xi2, …, xid}, yi∈ℝ,拟合目标是使得f(xi)=ωxi+bi,且f(xi)=yi。
其求解可转化为均方误差的最小化问题
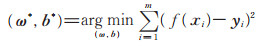
|
(1) |
当数据集D由多个属性构成,即得到多元线性回归
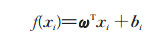
|
(2) |
当用线性回归模型的预测结果去逼近函数y= 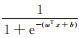
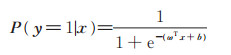
|
(3) |
其求解目标为
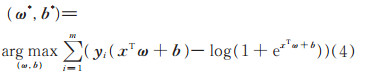
|
(4) |
2)支持向量机模型拟合给定数据集D= {(x1, y1), (x2, y2), …, (xm, ym)},其中,yi∈{-1, +1},支持向量机模型拟合的目标是找到具有最大间隔的划分超平面,即通过调节参数,使得支持向量的间隔最大,其求解目标函数为
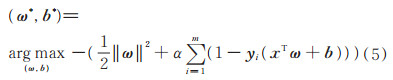
|
(5) |
从上述模型拟合问题的目标函数可以看出,传统监督学习中,通过训练数据集的迭代,调整模型拟合参数ω,最佳模型参数ω*使得拟合函数f(D, ω*)最大化,进而得到模型对数据集的表征学习。然而,可能涉及敏感数据集的模型拟合存在着不可预知的隐私泄露风险,这也就是本文的研究重点与价值所在。
1.2 差分隐私差分隐私保证了攻击者在具有最大化背景知识条件下敏感数据的安全性。隐私保护强度由隐私预算ε控制,隐私预算ε越小,保护强度越大,但噪声扰动也就越大。
定义3(兄弟数据集)[5]同域ϰ中数据集D和D′为兄弟数据集,当且仅当|D- D'| = 1,即两数据集只相差一条数据。
定义4(差分隐私)[5]给定兄弟数据集D、D′和随机函数f及其输出域O,函数f为ε-差分隐私,当且仅当输出概率P[]满足
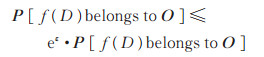
|
(6) |
差分隐私的主要实现机制包括Laplace机制和指数机制。指数机制主要应用在非数值型属性的选择方面。
差分隐私中全局敏感度是度量数据集变化对函数输出影响的重要参数,定义如下:
定义5(全局敏感度)[6]给定兄弟数据集D,D′,函数A的敏感度
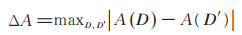
|
(7) |
定理1(指数机制)[7]给定分类型数据集Ω,类别ω∈ Ω服从打分函数Q(ω),当且仅当类别ω*被选择输出的概率P(ω*)服从参数为ΔQ(ω)/ε 的指数分布时,即exp(ε· (f(D, ω)- f(D', ω)) /Δ),
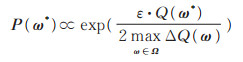
|
(8) |
则此过程满足指数机制下的ε-差分隐私(ΔQ为全局敏感度,证明参见文献[7])。
依据组合特性(证明参见文献[5]),差分隐私在监督学习的迭代优化中可以提供达到组合强度级别的隐私保护。
性质1(组合特性)[5]满足差分隐私的算法A1,
A2,…,An,其隐私预算分别为ε1,ε2,…,εn,则算法组合满足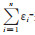
本文提出的满足差分隐私的监督学习模型拟合框架,以全局敏感度、指数机制、组合特性为理论基础,实现基于粒子群优化的差分隐私模型参数全局迭代优化。
1.3 粒子群优化算法1995年提出的粒子群优化算法(particle swarm optimization, PSO)基于种群内个体间协作和信息资源共享实现[17],在个体和群体最优的导向选择模式中,以粒子的位置、速度、适应度三元组为核心,其位置x(t)、速度v(t)的迭代更新公式为
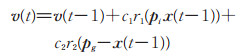
|
(9) |
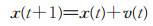
|
(10) |
其中,c1、c2、r1、r2为预设参数,pi和pg分别为个体最优和群体最优,适应度值与目标函数值对应。粒子群优化的全局收敛性由吸引子定理保证,证明参见文献[18],其中φ1=c1r1,φ2=c2r2。
定理2(吸引子定理)[18]对于简化的PSO模型,粒子位置序列{x(t)}满足如下极限
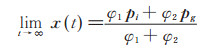
|
(11) |
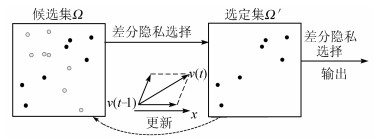
根据1.1节中的监督学习模型拟合问题定义,借鉴粒子群优化算法中个体和群体最优的导向选择模式,按照差分隐私中指数机制来实现模型学习性能与数据集隐私性保护的平衡,基于粒子群优化的差分隐私模型拟合算法(PSO-guided differential privacy fitting,PSO-DP),如算法1所示,其关键步骤如图 1所示。
|
| 图 1 算法框架关键步骤 Fig. 1 The key steps of the algorithm framework |
算法1 PSO-DP
Input:数据集D、拟合函数f、隐私预算ε,参数向量候选集Ω大小m,参数向量选定集Ω'大小m′,迭代次数t。
Output:最优参数ω*。
① 随机初始化具有m个参数向量候选集Ω;
FOR i=1 TO r
DO
② 隐私预算为ε/r,以差分隐私选择策略从候选集Ω中选择个体最优和群体最优参数向量,并存入参数向量选定集Ω';
③ 根据位置和速度更新公式(9)和(10),在选定集Ω'中选择个体最优和群体最优粒子来生成新的参数向量,并更新候选集Ω,进而按照差分隐私的方式向全局最优方向进化;
END FOR
④ 最后从选定集Ω'中按照改进的指数机制输出最优参数向量ω*。
在算法1中,参数向量候选集Ω大小m为粒子群优化中的种群大小,参数向量选定集为每轮迭代的个体最优和群体最优集合,步骤②中涉及的满足差分隐私的选择策略由算法2中DP-Select实现,其中,算法2中步骤③的指数机制将在2.2小节详细介绍。
算法2 DP-Select
Input:数据集D、拟合函数f、隐私预算ε′,参数向量候选集Ω,选定集大小m′。
Output:参数向量选定集Ω'。
① 初始化参数向量选定集Ω'为空集;
② 计算所有ω∈ Ω的f(D, ω);
FOR i=1 TO m′
DO
③ 按照参数为ε′/m′的指数机制来选择ω*,使得f(D, ω*)最大化;
④ 把ω*加入选定集Ω'并从候选集Ω中删除;
END FOR
⑤ 输出选定集Ω'。
2.2 改进的指数机制针对模型拟合中差分隐私选择策略,利用改进指数机制实现粒子群优化中个体最优和群体最优粒子的选择。主要改进体现在对指数机制的打分函数上,拟合函数在数据集D上的打分函数定义为
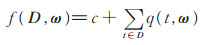
|
(12) |
其中,c为调节常数,q(t, ω)用来度量机器学习模型与D中数据t的拟合程度。由定理1可知,针对D,若输出参数向量ω服从exp(ε⋅f(D, ω)/Δ),则可以得到
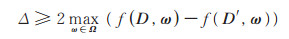
|
(13) |
Δ与全局敏感度密切相关,为全局敏感度2倍的上界。若全局敏感度远大于ε⋅f (D, ω*),则输出的ω* 概率几乎相同。为此,本文改进的指数机制采用的参数Δ具有更小下界,满足下式
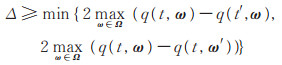
|
(14) |
引理1当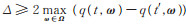
证 给定邻接数据集D、D′中任意记录t、t′,对任意拟合参数向量ω∈Ω,可以得到
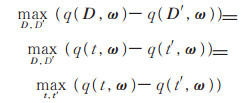
|
(15) |
引理2当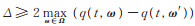
证 给定邻接数据集D、D′中任意记录t、t′,对于改进指数机制的任意输出ω∈Ω,可以得
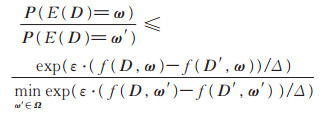
|
(16) |
结合公式(7),可以得到
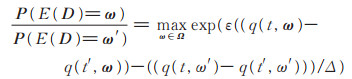
|
(17) |
由引理1得到
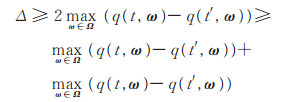
|
(18) |
可知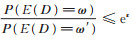
结合引理1和引理2,可证改进的指数机制满足差分隐私。结合定理2及差分隐私组合特性,可证基于粒子群优化的差分隐私拟合框架可以依概率收敛,并满足ε-差分隐私。
3 应用在回归、支持向量机模型中,基于粒子群优化的差分隐私拟合框架涉及的打分函数和与敏感度函数密切相关的参数Δ具体应用如下:
在线性回归模型拟合模型和logistic回归模型中,拟合函数分别为(1)式和(4)式,根据2.2节中改进的指数机制定义的打分函数,可以作如下设置,q(t, ω ) = y(xTω+ b) -log (1 + exp(xTω+ b)),同时根据(14)式,可以得到
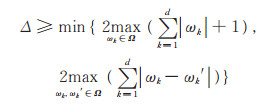
|
(19) |
在支持向量机模型拟合中,拟合函数为1.1节中的(5)式,根据改进的指数机制中定义的打分函数,可以设置
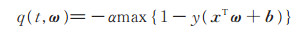
|
(20) |
同时根据公式(14),可以得到
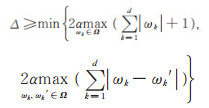
|
(21) |
此外,本文的算法框架及机制均可尝试给出机器学习中的神经网络、深度学习中的随机梯度下降算法的隐私保护解决方案。
4 结论本文针对监督学习模型拟合中涉及的训练数据集隐私保护问题,引入满足差分隐私的粒子群优化算法,按照改进的指数机制选择个体最优和群体最优粒,引导以参数向量形式编码的粒子进行全局寻优。理论证明,本文算法框架满足差分隐私,可以实现监督学习中训练数据集的敏感信息保护。最后给出了框架在回归、支持向量机模型参数优化过程中打分函数的设置方式。下一步工作将深入探索本文框架在多种深度神经网络中的应用途径。
致谢: 感谢“位智”和“武信”两个攻关小组对本文的大力支持。
| [1] |
NOZARI E, TALLAPRAGADA P, CORTES J. Differentially private distributed convex optimization via functional perturbation[J]. IEEE Transactions on Control of Network Systems, 2018, 5(1): 395-408. DOI:10.1109/TCNS.2016.2614100 |
| [2] |
高志强, 王宇涛. 差分隐私技术研究进展[J]. 通信学报, 2017, 38(S1): 151-155. GAO Z Q, WANG Y T. Survey on differential privacy and its progress[J]. Journal on Communications, 2017, 38(S1): 151-155. (Ch). |
| [3] |
GAO Z Q, SUN Y X, CUI X L, et al. Privacy-preserving hybrid K-means[J]. International Journal of Data Warehousing and Mining (IJDWM), 2018, 14(2): 1-17. DOI:10.4018/IJDWM.2018040101 |
| [4] |
高志强, 崔翛龙, 周沙, 等. 本地差分隐私保护及其应用[J]. 计算机工程与科学, 2018, 40(6): 1029-1036. GAO Z Q, CUI X L, ZHOU S, et al. Local differential privacy protection and its applications[J]. Computer Engineering & Science, 2018, 40(6): 1029-1036. DOI:10.3969/j.issn.1007-130X.2018.06.010 (Ch). |
| [5] |
DWOK C, RORHBLUM G N, VADHAN S.Boosting and Differential Privacy[DB/OL].[2018-04-02].http://privarytoos.seas.harvard.edu/files/privacytools/files/05670947.pdf.DOI: 10.1109/FOCS.2010.12.
|
| [6] |
DWORK C, POTTENGER R. Toward practicing privacy[J]. Journal of the American Medical Informatics Association Jamia, 2013, 20(1): 102-108. DOI:10.1136/amiajnl-2012-001047 |
| [7] |
DWORK C, MCSHERRY F, NISSIM K.Calibrating noise to sensitivity in private data analysis[C]// Theory of Cryptography LN CS(3876).Berlin: Springer, 2012: 265-284.
|
| [8] |
GAO Z Q, WANG Y T, DU AN, Y Y, et al. Multi-level privacy preserving data publishing[J]. International Journal of Innovative Computing and Applications, 2018, 9(2): 66-76. DOI:10.1504/IJICA.2018.092587 |
| [9] |
FANTI G, PIHUR V, ÚLFAR E. Building a RAPPOR with the unknown: Privacy-preserving learning of associations and data dictionaries[J]. Privacy Enhancing Technologies, 2016, 16(3): 41-61. DOI:10.1515/popets-20160015 |
| [10] |
ZHANG J, ZHANG Z, XIAO X, et al. Functional mechanism: Regression analysis under differential privacy[J]. Proceedings of the VLDB Endowment, 2012, 5(11): 1364-1375. DOI:10.14778/2350229.2350253 |
| [11] |
CHAUDHURI K, MONTELEONI C, SARWATE A D. Differentially private empirical risk minimization[J]. Journal of Machine Learning Research, 2011, 12(3): 1069-1109. |
| [12] |
RUBINSTEIN B I P, BARTLETT P L, HUANG L, et al. Learning in a large function space: Privacy-preserving mechanisms for SVM learning[J]. Journal of Privacy and Confidentiality, 2012, 4(1): 65-100. DOI:10.9774/GLEAF.978-1-909493-38-4_2 |
| [13] |
BOTTOU L, CURTIS F E, NOCEDAL J. Optimization methods for large-scale machine learning[J]. SIAM Review, 2018, 60(2): 223-311. DOI:10.1137/16M1080173 |
| [14] |
JORDAN M I, RUMELHART D E. Forward models: Supervised learning with a distal teacher[J]. Cognitive Science, 1992, 16(3): 307-354. DOI:10.1207/s15516709cog1603_1 |
| [15] |
RAFTERY A E, MADIGAN D, HOETING J A. Bayesian model averaging for linear regression models[J]. Journal of the American Statistical Association, 1997, 92(437): 179-191. DOI:10.1080/01621459.1997.10473615 |
| [16] |
VAPNIK V, GUYON I, HASTIE T. Support vector machines[J]. Machine Learn, 1995, 20(3): 273-297. |
| [17] |
LEBOUCHER C, SHIN H S, CHELOUAH R, et al. An enhanced particle swarm optimization method integrated with evolutionary game theory[J]. IEEE Transactions on Games, 2018, 10(2): 221-230. DOI:10.1109/TG.2017.2787343 |
| [18] |
POLI R, KENNEDY J, BLACKWELL T. Particle swarm optimization[J]. Swarm Intelligence, 2007, 1(1): 33-57. |
 2019, Vol. 65
2019, Vol. 65




