文章信息
- 苏航 , 刘建伟 , 刘巍然 , 李妍 . 2016
- SU Hang, LIU Jianwei, LIU Weiran, LI Yan . 2016
- 基于身份的高效层次认证密钥协商协议
- Efficient Hierarchical Identity-based Authenticated Key Agreement Protocol
- 武汉大学学报(理学版), 2016, 62(3): 249-254
- Journal of Wuhan University(Natural Science Edition), 2016, 62(3): 249-254
- http://dx.doi.org/10.14188/j.1671-8836.2016.03.007
-
文章历史
- 收稿日期:2015-08-10

2. 航天恒星科技有限公司, 北京 100086
2. Space Star Technology Company, LTD, Beijing 100086, China
密钥协商协议在安全通信中有至关重要的作用,它允许两个用户在开放信道上协商安全的会话密钥,以保证双方通信的安全. 1984年,Shamir[1]提出了基于身份的签名机制,至此,基于身份的密码体
制成为了密码学领域的研究热点. 在该体制中,用户可以选取自己的身份作为公钥,私钥由可信的私钥生成中心PKG生成. 不过,直到2001年,Boneh 和Franklin[2]才设计出第一个真正实用的基于Weil配对的基于身份的加密算法. 利用基于身份的加密体制,学者们提出了大量的基于身份的认证密钥协商协议. 然而,大多数基于身份的认证密钥协商协议[3~5]都是
在单一PKG环境下提出的. 在实际应用中,每一用户都需要与PKG交互以注册身份及生成私钥,随着用户的增多,单一PKG将不能承担起系统繁重的业务,成为该类协议应用的瓶颈,而且不同领域相对独立,不可能共享同一PKG. Gentry等人[6]、Boneh等人[7]和Ren等人[8]分别提出了基于身份的层次加密体制,该体制中包含一个根PKG及多层的域PKG,根PKG只对域PKG进行验证并为其生成私钥,上层域PKG验证下层域PKG并为其生成私钥,直至用户的上一层域. 利用基于身份的层次加密体制,Cao等人[9]和Liu等人[10]分别提出了基于身份的层次认证密钥协商协议,不过这些协议是基于椭圆曲线双线性对运算的,因此效率较低. Cao等人[11]提出了无双线性对运算的基于身份的密钥协商协议,Islam等人[12]增强了Cao等人的方案的安全性,使其能够抵抗临时私钥泄露攻击. 虽然文献[11, 12]方案不含双线性对映非运算,具有较高的效率,但依然不能解决单一PKG的瓶颈问题.
在空间信息网络中[13, 14],含有多种异构网络和大量网络节点,集中式的管理模式会因数据流过于集中,而导致网络拥塞和服务延时及单点失效问题. 空间节点的软硬件处理能力相对较低,处理资源和带宽相对较少,电源和推进能力有限. 对于部分实时性要求较高的任务,通常不允许在运算过程中耗费过多时间.
本文借助于Islam等人[12]的构造思想,提出一种新的无双线性对运算的基于身份的层次认证密钥协商协议.
1 预备知识 1.1 椭圆曲线椭圆曲线E/Fp可用等式表示为[15]:
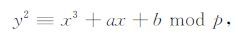
|
其中a,b∈Fp且4a3+27b2≠0 mod p群G={(x,y)|x,y∈Fp,(x,y)∈E/Fp}∪{O},O为无穷远点.
群G为循环加法群,群运算为加法运算(点乘运算),描述如下:
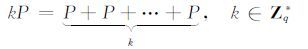
|
计算性Diffie-Hellman问题(computational Diffie-Hellman problem,CDH问题):G为q阶的循环加法群,给定P,aP,bP∈G(a,b∈ Zq*是未知的随机数),计算abP∈G.
定义1 多项式时间算法A在安全常数λ下解决CDH问题的优势定义如下
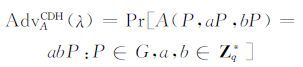
|
定义2 CDH困难假设指出,不存在多项式时间算法A,使其具有不可忽略的优势
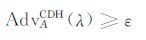
|
可以解决CDH问题.
1.3 基于身份的层次密钥协商协议定义结合基于身份的层次加密算法定义[6~8]及密钥协商过程[12, 16, 17],本节给出基于身份的层次认证密钥协商协议的定义:
1) (pp,msk)←Setup(λ):系统建立算法Setup以安全常数λ∈N作为输入,输出系统的全局性公共参数pp及主私钥msk;
2) (d)←KeyGen(msk,ID):私钥生成算法KeyGen以主密钥msk和任意一个用户身份向量ID=(I1,I2,…,It)作为输入,输出为该用户ID所对应的私钥d;
3) (d)←Delegate(d′,ID):私钥托管算法Delegate以用户身份向量ID′=(I1,I2,…,It-1)的私钥d′、用户身份向量ID=(I1,I2,…,It)作为输入,输出为用户ID的私钥d;
4) (T)←Temporary(d):临时信息生成算法Temporary以用户私钥d作为输入,输出为用于密钥协商阶段的临时信息T;
5) (sk)←Agreement(pk′,T′,d):密钥协商算法Agreement以参与密钥协商的用户的私钥d和另一用户的公钥pk′及其临时信息T′作为输入,输出为协商的会话密钥sk.
Temporary、Agreement为参与密钥协商的用户分别执行. 对于任意用户ID1,其私钥为d1,公钥为pk1. 任意用户ID2,其私钥为d2,公钥为pk2. 任意T1=Temporary(d1),任意T2=Temporary(d2). 任意sk1=Agreement(pk′,T′,d1),任意sk2=Agreement(pk″,T″,d2). 只要pk′=pk2,T′=T2,pk″=pk1,T″=T1,则必sk1=sk2,用户可协商得到相同的会话密钥.
1.4 密钥协商协议安全需求密钥协商协议在安全通信中有至关重要的作用,密钥协商协议的安全关系着整个通信过程的安全. 在总结前人工作[3~5, 9, 12, 16, 17]的基础上,本节给出了以下认证密钥协商协议所需的安全需求:
1) 已知会话密钥安全(known-key security):某次会话密钥的泄露不会影响另一会话密钥的安全;
2) 前向安全(forward security,FS):当一个或多个用户的长期私钥泄露时,已建立的会话密钥不受影响;
3) 完美前向安全(perfect forward security,PFS):当所有用户的长期私钥均泄露时,已建立的会话密钥不受影响;
4) PKG前向安全(PKG forward security,PKG-FS):当系统的主私钥泄露时,不会影响会话密钥的安全性;
5) 无密钥泄露模仿(key-compromise impersonation,KCI):当用户A的长期私钥泄露时,攻击者可以在与其他用户的会话中模仿A,但是不能模仿其他用户与A会话;
6) 未知密钥共享(unknown-key share,UKS):当用户A与用户B建立会话密钥后,A可以确认他是与B而不是与其他用户进行会话,即可以认证对方的身份;
7) 无密钥控制(no key control):任何用户都不能强迫密钥被预先选择或预测密钥.
2 协议设计 2.1 协议描述本文基于身份的层次认证密钥协商协议包括Setup、KeyGen、Delegate、Temporary、Agreement五部分,协议的具体构造过程如下:
1) (pp,msk)←Setup(λ):系统建立算法选取满足安全常数λ∈N的阶为q的椭圆曲线循环加法群G,即|q|=λ,G的生成元为P. 选取安全的哈希函数:H1:0,1*→Zq*,H2:{0,1}*→K,其中K为会话密钥空间. 选取主私钥msk=s,s∈Zq*. 计算公钥Ppub=sP. 输出共享的全局性系统参数:
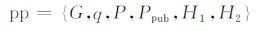
|
2) (d)←KeyGen(msk,ID):给定主私钥msk和任意一个用户身份向量ID=(I1,I2,…,It),私钥生成算法随机选取g1,…,gt∈Zq*,计算ri=H1(Ii‖giP),其中1≤i≤t. 输出该用户所对应的私钥:
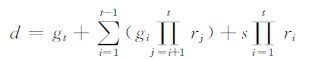
|
(1) |
若d=0,则需要重新选取g1,…,gt∈Zq*. 通过安全信道将{g1P,…,gtP,d}发送给用户ID,其中g1P,…,gtP为用户的部分公钥. 用户验证等式:
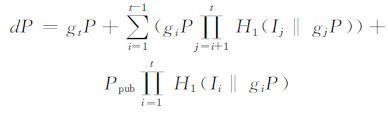
|
(2) |
若等式不成立,则拒绝此私钥.
3) (d)←Delegate(d′,ID):给定用户ID′=(I1,I2,…,It-1)的私钥d′,其部分公钥为{g1P,…,gt-1P}.用户ID′为用户ID=(I1,I2,…,It)生成私钥. 密钥托管算法随机选取gt∈Zq*,计算rt=H1(It‖gtP),生成私钥d:
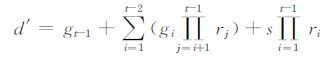
|
(3) |
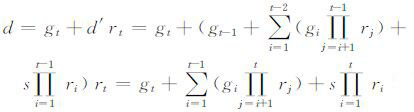
|
(4) |
若d=0,则需要重新选取gt∈Zq*. 通过安全信道将{g1P,…,gtP,d}发送给用户ID,其中g1P,…,gtP为用户的部分公钥. 用户验证等式(2),若等式不成立,则拒绝此私钥.
以用户A和B为例,其中用户A所处的层级为lA,IDA=(I1,I2,…,IlA),A的私钥为dA,公钥pkA为{IDA,g1P,…,glAP}. 用户B所处的层级为lB,IDB=(I′1,I′2,…,I′Bl),B的私钥为dB,公钥pkB为{IDB,g′1P,…,g′BlP}.
4) (T)←Temporary(d):用户A和B分别执行临时信息生成算法,A 随机选取a∈Zq*,计算TA=adAP,发送{TA,pkA}给B. B随机选取b∈Zq*,计算TB=bdBP,发送{TB,pkB}给A.
5) (sk)←Agreement(pk′,T′,d):用户A和B分别执行密钥协商算法,计算会话密钥:
A计算:
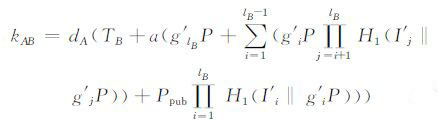
|
(5) |
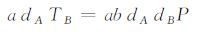
|
(6) |
会话密钥为:skA=H2(kAB‖abdAdBP)
B计算:
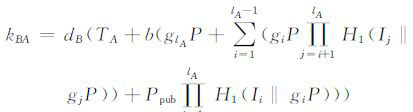
|
(7) |
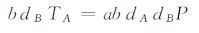
|
(8) |
会话密钥为:skB=H2(kBA‖abdAdBP).
2.2 协议正确性要证明协议中用户A和B获得相同的会话密钥,即skA=skB,只需证明kAB=kBA,证明如下:
用户A做如下计算:
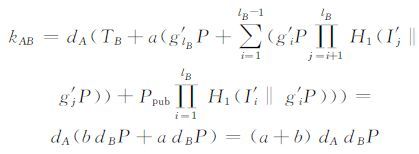
|
用户B做如下计算:
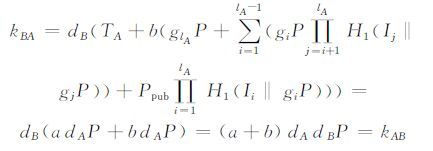
|
因此,用户A与用户B可计算获得相同的会话密钥.
3 安全性分析本节将针对密钥协商的安全需求对本文协议的安全性进行分析,本文协议具有以下安全性质:
1) 已知会话密钥安全:在进行密钥协商时,用户A与用户B随机选取临时私钥a和b,会话双方建立的会话密钥为
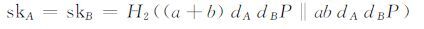
|
可知,会话密钥中含有临时私钥信息,因此两次密钥协商建立的会话密钥是相互独立的. 即使攻击者得到了某次协商过程的会话密钥,也不能计算出其他协商过程建立的会话密钥.
2) 完美前向安全:此时,用户A和B的长期私钥均泄露,攻击者可获得的信息为:dA、dB、adAP、bdBP、dAP、dBP.
假设H2为随机预言机,给定CDH问题实例U=adAP,V=bdBP,W=CDH(U,V)=abdAdBP. 假设攻击者正确计算出会话密钥skA=H2(kAB‖abdAdBP)的优势为AdvA(sk),且不可忽略. 则攻击者正确计算出W的优势为:
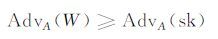
|
即攻击者解决CDH问题的优势不可忽略,这与CDH困难假设相悖. 因此,攻击者正确计算出会话密钥的优势AdvA(sk)是可忽略的,可保证协议的完美前向安全性.
3) PKG前向安全:当系统的主私钥泄漏时,由(1)式可知,攻击者不能得到关于会话双方的长期私钥和临时私钥的任何信息. 因此,攻击者可获得的信息仅为adAP、bdBP.
假设H2为随机预言机,给定CDH问题实例U=adAP,V=bdBP,W=CDH(U,V)=abdAdBP. 由2)可知,攻击者正确计算出abdAdBP的优势AdvA(W)是可忽略的. 因此,可保证协议的PKG前向安全.
4) 无密钥泄露模仿:假设用户A的长期私钥泄露,攻击者若想模仿用户B与A会话,必须能够正确计算出kAB. 此时,攻击者容易获得的信息为dA、adAP、cP(攻击者选取的TB)、dAP、dBP. 则
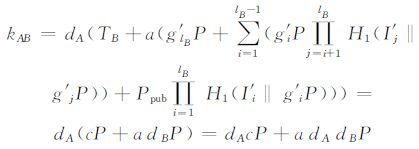
|
假设H2为随机预言机,给定CDH问题实例U=adAP,V=dBP,W=CDH(,V)=adAdBP. 假设攻击者正确计算出kAB=dAcP+adAdBP的优势为AdvA(kAB),且不可忽略. 则攻击者正确计算出W的优势为:
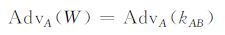
|
即攻击者解决CDH问题的优势不可忽略,这与CDH困难假设相悖. 因此,攻击者正确计算出kAB的优势AdvA(kAB)是可忽略的.
假设H2为随机预言机,给定CDH问题实例U=adAP,V=dBP,W=CDH(U,V)=abdAdBP. 由(2)可知,攻击者正确计算出abdAdBP的优势是可忽略的.
因此,攻击者正确计算出会话密钥的优势AdvA(sk)是可忽略的. 协议可抵抗密钥泄露模仿攻击.
5) 未知密钥共享:在密钥协商过程中,需要根据对方的身份及公钥生成的含有对方私钥信息的参数计算会话密钥,可以隐式认证对方的身份.
6) 无密钥控制:密钥协商过程中需要用到会话双方的身份信息、公钥及由会话双方提供的临时信息,由双方共同参与计算会话密钥,可以保证无密钥控制.
4 效率分析 4.1 协议复杂度本节对本文协议的计算复杂度进行分析,并与同类协议[9, 10]对比,结果如表1所示. 在分析计算复杂度时,主要考虑的计算类型有:椭圆曲线上的双线性对运算、循环加法群G中点乘运算及双线性群GT中的指数运算及哈希函数运算. 用P表示双线性对运算耗时,M表示点乘运算耗时,E表示双线性群GT中的指数运算耗时,H表示哈希函数H:{0,1}*→G的运算耗时. 对于有系统最大层级限制的方案,用L表示系统最大层级. l表示用户所处层级,lA,lB为用户A和B的层级,i表示为用户A和B在第i层有相同的节点.
为了对比协议的计算开销,本节选取jpbc库中两种椭圆曲线进行测试,同等安全水平的A类椭圆曲线和F类椭圆曲线的相关参数,如表2所示.
| E/Fp | Type A | Type F |
| 曲线方程 | y2=x3+x | y2=x3+b |
| G群阶数 | 512 bit | 160 bit |
| Zq*域阶数 | 160 bit | 160 bit |
表3为测试平台的相关信息. 本节对A类曲线和F类曲线中的单次双线性对运算、G群点乘运算(即指数运算)、G群乘法运算、GT群指数运算、GT群乘法运算、Zq*域乘法运算、Zq*域加法运算及哈希函数运算的耗时分别进行了测试,结果如表4所示.
| 项目 | 参数 | |
| CPU型号 | Intel Core i3-E7400 | |
| CPU主频 | 2.80 GHz×2 | |
| 内存 | 4 GB | |
| 系统类型 | Win7-32 bit | |
| 软件平台 | Eclipse + JDK1.7.0 | |
| jpbc库版本 | 2.0.0 |
| 测试项目 | Type A | Type F |
| 双线性对运算 | 38.56 | 291.86 |
| G群点乘运算 | 32.74 | 6.58 |
| G群乘法运算 | 0.17 | 0.05 |
| GT群指数运算 | 4.62 | 67.12 |
| GT群乘法运算 | 0.04 | 0.48 |
| Zq*域乘法运算 | 0.01 | 0.016 |
| Zq*域加法运算 | 0.01 | 0.012 |
| H:0,1*→Zq* | 0.17 | 0.14 |
| H:0,1*→G | 75.64 | 0.55 |
为了对比三种协议的执行效率,本节实现了上述三种协议并对其进行测试. 由于F类曲线生成的循环群是非对称的,因此前两种协议只使用A类曲线实现. 假设系统层级为7,表5、表6分别为KeyGen和Delegate算法的执行耗时. 在Agreement算法中,本节选取三种情形进行测试,假设用户所处层级为别为lA=2,lB=7,i=1、lA=4,lB=6,i=3、lA=5,lB=5,i=4. 测试结果如表7所示.
测试结果表明,与同类协议相比,本文协议具有较高的执行效率. 私钥生成算法耗时与用户所处层级成线性关系,私钥托管算法耗时为常数. 在私钥生成算法和私钥托管算法方面,本文协议具有同类协议不可比拟的优势. 密钥协商算法耗时与用户A和B所处层级之和成线性关系. 虽然随着用户所处层级增加,本文协议在密钥协商阶段耗时将增加,此时,在A类曲线中本文协议的优势将会减小,但是在同等安全水平的F类曲线中,本文协议依然具有同类协议不可比拟的优势.
5 结论本文提出了一种新的无双线性对运算的基于身份的层次认证密钥协商协议,并对协议的安全性和效率进行了分析. 分析表明,本文协议具有已知密钥安全、完美前向安全、PKG前向安全等安全性质,能够抵抗基于私钥泄露的伪装攻击. 与同类协议相比,本文协议不包含双线性对运算,具有较高的执行效率. 本文协议对系统层级深度没有限制,扩大了基于身份的层次认证密钥协商协议的适用范围.
| [1] | SHAMIR A. Identity based cryptosystems and signature schemes[C]//Advances in Cryptology Crypto84. Berlin: Springer-Verlag, 1984: 47-53. |
| [2] | BONEH D, FRANKLIN M. Identity-based encryption from the Weil pairing[C]//Advances in Cryptology Crypto2001. Berlin: Springer-Verlag, 2001: 213-229. |
| [3] | SHIM K. Efficient ID-based authenticated key agreement protocol based on Weil pairing[J]. Electronics Letters, 2003, 39 (8) : 653 –654. |
| [4] | RYU E K, YOON E J, YOO K Y. An efficient ID-based authenticated key agreement protocol from pairings[C]//Networking 2004. Berlin Heidelberg: Springer, 2004: 1458-1463. |
| [5] | NI L, CHEN G L, LI J H, et al. Strongly secure identity-based authenticated key agreement protocols in the escrow mode[J]. Science China Information Sciences, 2013, 56 (8) : 1 –14. |
| [6] | GENTRY C, SILVERBERG A. Hierarchical ID-based cryptography[C]//Advances in Cryptology—ASIACRYPT2002. Berlin Heidelberg: Springer, 2002: 548-566. |
| [7] | BONEH D, BOYEN X, GOH E J. Hierarchical identity based encryption with constant size ciphertext[C]//Advances in Cryptology-EUROCRYPT 2005. Berlin Heidelberg:Springer, 2005: 440-456. |
| [8] | REN Y, GU D. Secure hierarchical identity based encryption scheme in the standard model[C]//Progress in Cryptology-INDOCRYPT 2008. Berlin Heidelberg:Springer, 2008: 104-115. |
| [9] | 曹晨磊, 刘明奇, 张茹, 等. 基于层级化身份的可证明安全的认证密钥协商协议[J]. 电子与信息学报, 2014 ,36 (12) : 2848 –2854. CAO C L, LIU M Q, ZHANG R, et al. Provably secure authenticated key agreement protocol based on hierarchical identity[J]. Journal of Electronics & Information Technology, 2014, 36 (12) : 2848 –2854. |
| [10] | LIU W, LIU J, WU Q, et al. SAKE: scalable authenticated key exchange for mobile e-health networks[DB/OL]. [2015-02-03].http://onlinelibrary.wiley.com/doi/10.1002/sec.1198/epdf. |
| [11] | CAO X, KOU W, DU X. A pairing-free identity-based authenticated key agreement protocol with minimal message exchanges[J]. Information Sciences, 2010, 180 (15) : 2895 –2903. |
| [12] | ISLAM S K H, BISWAS G P. An improved pairing-free identity-based authenticated key agreement protocol based on ECC[J]. Procedia Engineering, 2012, 30 : 499 –507. |
| [13] | TONG D, LIU J W, MAO K F, et al. Certificateless and pairing-free key agreement scheme for satellite network[DB/OL].[2012-02-20].http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6992230 IET. |
| [14] | WANG Z, DU X, SUN Y. Group key management scheme based on proxy re-cryptography for near-space network[DB/OL].[2015-02-21].http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5948688. |
| [15] | HANKERSON D, VANSTONE S, MENEZES A J. Guide to Elliptic Curve Cryptography. New York: Springer Science & Business Media.[M] 2004 . |
| [16] | HE D, CHEN J, HU J, A pairing-free certificateless authenticated key agreement protocol[DB/OL].[2015-03-10]. http://onlinelibrary.wiley.com/doi/10.1002/ dac.1265/epdf. DOI:10.1002/dac.1265. |
| [17] | HE D, CHEN Y, CHEN J, et al. A new two-round certificateless authenticated key agreement protocol without bilinear pairings[J]. Mathematical and Computer Modelling, 2011, 54 (11) : 3143 –3152. |
 2016, Vol. 62
2016, Vol. 62





