文章信息
- 刘双根, 丁媛媛, 施瑞, 卢士美
- LIU Shuanggen, DING Yuanyuan, SHI Rui, LU Shimei
- GF(2m)椭圆曲线上的Co_Z 点加算法
- Co_Z Addition on Elliptic Curves over Finite Fields GF(2m)
- 武汉大学学报(理学版), 2019, 65(2): 207-212
- Journal of Wuhan University(Natural Science Edition), 2019, 65(2): 207-212
- http://dx.doi.org/10.14188/j.1671-8836.2019.02.010
-
文章历史
- 收稿日期:2018-07-02

自20世纪80年代中期椭圆曲线密码体制(elliptic curve cryptography, ECC)[1, 2]被提出之后,由于其密钥短,运算量相对较少,安全性能高等优势,已被广泛应用在资源受限的硬件设备中[3]。ECC的安全性依赖于离散对数问题的难解性,如果攻击者能很容易从用户的公钥中计算出私钥,那么这个密码体制就是不安全的。在ECC中,标量乘算法kP(k为用户的私钥,P 为用户选取的椭圆曲线上的一有理点)是最耗时,也是最关键的算法。当攻击者截获或根据消耗轨迹推算出标量k,就能破解椭圆曲线加密,因此,标量乘的安全决定着整个椭圆曲线密码体制的安全性。而标量乘的运算易受到侧信道攻击(side channel attack, SCA)[4]。
标量乘算法的运行速度决定着整个ECC的实现效率,因此通过提高标量乘的运行速度,可以提高ECC的效率。标量乘算法主要包括两个层次:上层标量k 的展开;底层有限域内点加、倍点的域乘、域平方、求逆等基础运算[5],本文重点研究底层。Co_Z 点加运算在2007年由Meloni[6]首次提出,该运算通过统一椭圆曲线上两射影点的Z 坐标,使点加运算量降低,得出了新的点加算法,并将其应用在Euclidean加法链和Zeckendorf展开式中,通过减少点加运算中的域乘和域平方计算次数提高标量乘效率。近几年,Goundar、Wei等[7, 8]将Co_Z 算法应用到Montgomery阶梯算法、Joy倍点点加算法和NAF(non-adjacent form)算法,优化了Weierstrass椭圆曲线上的标量乘运算公式。2017年,于伟等[9]在Montgomery算法的基础上,首次利用统一Z 坐标技巧,改进了有限域GF(3m)上椭圆曲线的点加和倍点公式。本文,我们提出特征2有限域椭圆曲线上的Co_Z 点加运算,推导出不同射影坐标系下的点加及三倍点(3P)运算公式。
1 背景知识 1.1 有限域GF(2m)上的椭圆曲线定义在域K 上的一个Weierstrass方程
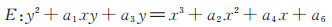
|
通过变量的相容性,可以简化方程。根据域K的特征不同,将椭圆曲线分为3种情况:特征不等于2或3、特征等于2和特征等于3。
当域K 的特征不等于2或不等于3时,通过相容性变换,曲线E 可简化为:y2 = x3 + ax + b, 其中a, b ∈ K。曲线的判别式是Δ = -16(4a3 + 27b2)。
若域K 的特征是3,则其非超奇异椭圆曲线[10]简化为:y2 = x3 +ax2 + b,其中a, b ∈ K,Δ =- a3b。
本文研究的重点是特征为2的非超奇异椭圆曲线,其Weierstrass方程可简化为:y2 + xy = x3 + ax2 + b,Δ = b。
根据“弦和切线”法则[11],有限域GF(2m)上的两点相加得到椭圆曲线上的第三点。椭圆曲线上的点集合及这种加法运算构成了一个加法交换群,∞为加法交换群的无穷远点。因此,有限域GF(2m)上的非超奇异椭圆曲线的群运算法则为:
1)单位元
对于所有的P ∈ E (GF (2m)),P + ∞ = ∞ + P
2)负元素
如果P = (x, y ) ∈ E (GF (2m)),则(x, y )+(x, x + y )= ∞。记点(x, x + y )为-P,并称其为P 的负。注意,-P 也是E (GF (2m))上的一点。
3)点加
令P = (x1, y1) ∈ E (GF (2m)), Q= (x2, y2) ∈E (GF(2m)),P ≠ Q, 则P + Q = (x3, y3)。其中
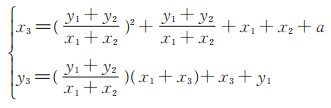
|
(1) |
4)倍点
令P = (x1, y1) ∈ E (GF (2m)),P ≠ - P, 则2P =(x3, y3)。其中

|
(2) |
由此可得出,仿射坐标系下,点加运算量为1次求逆(I),1次平方(S)和2次乘(M);倍点运算量为1I+1S+2M。由于求逆的计算代价较高,因此通过转换坐标系,避免运算公式中出现求逆,可降低点加和倍点的运算代价[12]。
1.2 射影坐标下的点加和倍点运算公式本文中,我们考虑两种射影坐标下的点加和倍点运算。
1.2.1 López & Dahab射影坐标射影点(X:Y:Z ), Z ≠ 0与仿射点(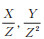

|
令P = (X1:Y1:Z1), Q = (X2:Y2:Z2), P + Q = (X3:Y3:Z3)。若P ≠ Q, 则点加运算公式为
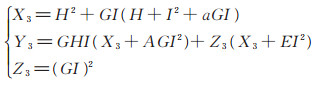
|
(3) |
其中:A = X1Z2,B = X2Z1,C = Z12,D = Z22,E = Y1D,F = Y2C,G = Z1Z2,H = E + F,I = A + B。其倍点运算公式为
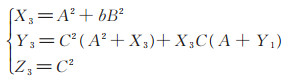
|
(4) |
其中:A = X12, B = Z12, C = X1Z1。
根据运算公式,可以看出一次点加运算量为13M + 5S,一次倍点运算量为4M + 5S。当假设Z2 = 1时,点加运算量降至10M + 5S。López等[13]改进了倍点运算,将运算量降低到3M+5S。
1.2.2 Jacobian射影坐标射影点(X:Y:Z ), Z ≠ 0与仿射点P =(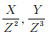
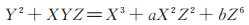
|
令P = (X1:Y1:Z1),Q = (X2:Y2:Z2),P + Q = (X3:Y3:Z3)。若P≠Q,则点加运算公式为

|
(5) |
其中:A = Z12,B = Z22,C = X1B,D = X2A,E = Z1Z2,F = Y1Z2,G = Y2Z1,H = FB + GA,I = E (C + D ),J = C + D。其倍点运算公式为

|
(6) |
其中:A = X12,B = Z12,C = X1B,D = Y1Z1。
根据运算公式,可以看出一次点加运算量为14M+5S,一次倍点运算量为4M+5S。假设Z2= 1时,点加运算量将降到10M+3S。
2 Co_Z点加运算和3P 运算 2.1 射影坐标下的Co_Z 点加运算令集合K3\ {(0:0:0)}是有限域GF(2m)上的非零三维向量的集合,其上的投影点存在如下等价关系

|
通过这一关系,我们可以将椭圆曲线上的两点P = (X1:Y1:Z1), Q = (X2:Y2:Z2)通过坐标处理,共享Z 轴,这就是Co_Z 的主要思路。上节给出了射影坐标下的点加运算公式,当引入Co_Z 后,可以推导出射影坐标系下改进后的Co_Z 点加运算公式。
2.1.1 López & Dahab射影坐标下的Co_Z 点加López & Dahab射影坐标下的两点P, Q 在仿射坐标下表示为
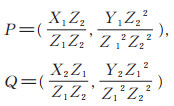
|
再转换为射影坐标,则得到

|
因此可将P, Q 两点转换为Z 坐标相同的点。
令初始点P = (X1:Y1:Z ),Q = (X2:Y2:Z )统一Z 坐标,则P + Q = (X3:Y3:Z3)的计算公式如下

|
(7) |
可将其简化为
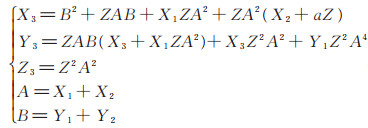
|
(8) |
P+Q 点中X、Y 轴坐标满足(X1ZA2:Y1Z2 A4: Z2 A2)~(X1:Y1:Z ),因此Co_Z 点加运算的输出点P+Q 和输入点P 具有相同的Z 坐标,而统一Z 轴变换已经在Co_Z 点加运算中计算出来,所以不需要额外的运算量。点加算法如算法1。
| 算法1 López & Dahab射影坐标下Co_Z 点加算法(LDCo_Z-ADD) |
| 输入:Co_Z(P, Q ), P = (X1:Y1:Z ),Q = (X2:Y2:Z ) |
| 输出:P + Q = (X3:Y3:Z3),P = (X1′:Y1′:Z3) |
| A ← (X1 + X2)2;B ← ZA; |
| C ← Z (X1 + X2);D ← B (X2 + aZ ); |
| X3 ← (Y1 + Y2)2 + C (Y1 + Y2)+ X1B + D; |
| Y3 ← C (Y1 + Y2)(X3 + X1B )+ X3C2 + Y1AZ3; |
| Z3 ← ZB; |
| X1′ ← X1B;Y1′ ← Y1AZ3; |
| 返回((X3:Y3:Z3),(X1′:Y1′:Z3)) |
算法1所需运算量为10M+3S,比Z2 = 1时的点加运算量减少了2S。由于在算法1计算过程中,输入点P 与输出点P+Q 的Z 轴的统一运算量较大,因此在López & Dahab射影坐标下Co_Z 点加的效率提升不是很明显。
2.1.2 Jacobian射影坐标下的Co_Z 点加运算令初始点P = (X1:Y1:Z ), Q = (X2:Y2:Z ),统一Z 坐标,则P + Q = (X3:Y3:Z3)的计算公式可简化为
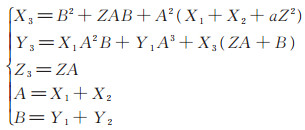
|
P+ Q 点中X、Y 轴坐标满足(X1A2:Y1A3:ZA ) ~(X1:Y1:Z ),因此Co_Z 点加运算的输出点P+ Q和输入点P 具有相同的Z 坐标,而统一Z 轴变换已经在Co_Z 点加运算中计算出来,所以不需要额外的运算量。点加算法如算法2。
| 算法2 Jacobian射影坐标下Co_Z 点加算法(JCo_Z-ADD) |
| 输入:Co_Z(P, Q ), P = (X1:Y1:Z ),Q = (X2Y2:Z ) |
| 输出:P + Q = (X3:Y3:Z3),P = (X1′:Y1′:Z3) |
| A ← (X1 + X2)2;B ← (Y1 + Y2)2; |
| C ← X1 + X2;D ← X1A; |
| E ← Y1C; |
| X3 ← B + Z3 (Y1 + Y2)+ D + A(X2 + aZ2); |
| Y3 ← D (Y1 + Y2)+ AE + X3 (Z3 + Y1 + Y2); |
| Z3 ← ZC; |
| X1′ ← X1A;Y1′ ← Y1AC; |
| 返回((X3:Y3:Z3),(X1′:Y1′:Z3)) |
Jacobian射影坐标下Co_Z 点加操作所需运算量为8M + 3S,比Z2 = 1时的点加运算量减少了2M。
2.2 有限域GF (2m)上的3P 运算本小节将计算有限域GF (2m)下的3P 运算,首先回顾一下倍点的运算公式。
令P = (x1, y1),2P = (x2, y2),其中

|
计算3P = 2P + P = (x3, y3),Dimitrov等[14]给出了仿射坐标系下的3P 运算公式

|
因此,仿射坐标系下计算一次3P 运算量为1I+ 3S+ 6M,这种算法比文献[15]减少了1M + 1S.在Dimitrov提出的3P 运算公式的基础上,可以推导出射影坐标下的3P 运算公式。本文对输入点的Z 坐标进行特殊化处理,能够改进3P 运算公式,减少运算量。
2.2.1 López & Dahab射影坐标下的3P 运算2008年,顾海华[16]提出一种López & Dahab射影坐标下的3P 运算公式(TPL):3P = (X3:Y3:Z3),则

|
其中: A = X12,B = X1Z1,C = AB,D = A - Y1,E = aB2 - D (D + B ),F = C + E,G = BC + FD,H = B2E。
这种López & Dahab射影坐标下的3P 运算量为12M+4S。
2.2.2 Jacobian射影坐标下的3P 运算Jacobian射影坐标下的3P = (X3:Y3:Z3),运算经过简化可以写成

|
其中:E = X1Z12 + X2,F = EZ2,G = Y1X13Z13 + Y2,H = aF2 + G (G + F )+ E3,X2 = X14 + bZ18,Y2 = X14Z2 +(X12 + Y1Z1 + Z2) X2,Z2 = X1Z12。
因此,此3P 运算量为13M+7S。
对Z 坐标进行特殊化处理,当Z1 = 1时,可以得出改进后的3P 运算公式。通过分析可知,改进后的3P 运算代价为12M+3S,具体算法如算法3。
| 算法3 Jacobian射影坐标下新3P 算法(New-TPL) |
| 输入:P = (X1:Y1:1) ∈ E (GF (2m)) |
| 输出:3P = (X3:Y3:Z3) |
| A ← X12;B ← X1Y1; |
| C ← X13;D ← C + X2; |
| E ← AB;F ← E + Y2; |
| X2 ← A2 + b; |
| Y2 ← X1A2 + X2 (A + Y1 + X1); |
| X3 ← F (F + X1D )+ D2 (D + aA ); |
| Y3 ← D2 (CF + ED )+ X3 (X1D + F ); |
| Z3 ← X1D; |
| 返回(X3:Y3:Z3) |
标量k 可展开成对称三进制形式(symmetric ternary form,STF)[17],相对二进制形式,它能够缩短展开后的链长,减少点加和3P 运算次数。将对称三进制应用到标量乘运算中,具体的标量乘算法可参考文献[3].在对称三进制标量乘算法中,每轮迭代中只有当ki ≠ 0时,才执行点加运算,而根据对称三进制的展开式,非零数出现的概率为2/3,因此其运算代价为n (T + 2A/3), 其中A 表示点加的运算代价,T 表示3P 的运算代价。
为提高标量乘的安全性,使其能够抵御简单能量攻击(simple power analysis, SPA),通过增加标量乘算法的运算量,文献[18]提出了一种可抵御SPA攻击的对称三进制标量乘算法。将本文提出的点加和3P 运算公式与文献[18]算法相结合,可优化标量乘算法的效率,如算法4。
| 算法4 Co_Z 对称三进制标量乘算法 |
| 输入:P, STP(k ) |
| 输出:kP |
| Q0 = ∞,P0 = ∞,P1 = P,P-1 = -P; |
| for i = n - 1 to 0, i - - |
| Q0 ← New - TPL(Q0); |
| Q1 ←Co_Z(Q0, Pki); |
| Q-1 ←Q1; |
| Q0 ←Qki; |
| end for |
| 返回Q0 |
在算法4中,每轮循环都需要执行一次Co_Z 点加和一次3P 运算,因此整个标量乘算法的运算量为n(A+T)。文献[18]中的可抵御SPA攻击的对称三进制标量乘算法采用的是仿射坐标系,每轮循环运算量为2I+ 5S+ 9M,这里求逆与域乘的运算量之比为8。由于在算法4中引入了Co_Z 点加算法,减少了每轮循环中点加和3P 运算所需的M、S计算次数,因此提高了运算效率。
3 运算效率分析将本文提出的Co_Z 点加、3P 运算公式应用到文献[3]的对称三进制标量乘算法中,比较不同运算公式下的标量乘算法运算效率(见表 1). 160-bit对称三进制标量乘算法的运算量为101(T + 2A/3)。
| 坐标系 | 点加(A) | 3P(T) | 标量乘 | |
| Lopez & Dahab射影坐标 | Co_Z | 10M+3S | 12M+4S | 1885M+606S |
| Jacobian射影坐标 | Z2 = 1 | 10M+3S | 13M+7S | 1986M+909S |
| Co_Z | 8M+3S | 12M+3S | 1751M+505S | |
在有限域GF (2m)内,平方运算更加高效,因此在二元域内,可以忽略计算平方(S)的时间[12],只比较计算域乘所需要的时间代价。Jacobian射影坐标下,当Co_Z 点加与3P 运算应用到对称三进制标量乘算法中,算法的运算效率提高了12%。若在Jacobian射影坐标和López & Dahab射影坐标下均使用Co_Z 点加运算公式,则对称三进制标量乘算法在Jacobian射影坐标的运算效率要比López & Dahab射影坐标下提高8%。
在160-bit下,对称三进制标量乘算法的运算量为101(T + A )。表 2给出了使用不同点加、3P 运算公式时,可抵御SPA攻击对称三进制标量乘算法的运算量。在Jacobian射影坐标下,改进后的点加、3P运算公式后得到的运算量为2020M+606S,此即为算法4的运算量。
当引用Co_Z 操作后,López & Dahab射影坐标下的点加运算量由10M+5S降至10M+3S;Jacobian射影坐标下的点加运算量由10M+3S降至8M+3S。新提出的Jacobian射影坐标下3P运算公式比之前的少了1M+4S。由表 2可知,Jacobian射影坐标下,结合了Co_Z点加和改进后的3P运算的算法4的运算效率,相比使用改进前的点加、3P运算公式的可抵御SPA攻击对称三进制标量乘算法提高了13%(只比较计算域乘所需要的时间代价)。
4 结论本文对有限域GF (2m)内的点加、3P 运算公式进行改进,使得运算过程中的域乘、域平方计算次数得到减少。当引入Co_Z 思想后,通过统一输入点的Z 坐标,López & Dahab射影坐标下Co_Z 点加运算量降低了2S;Jacobian射影坐标下Co_Z 点加运算量降低了2M。此外,当输入点的Z 轴特殊化处理为1后,Jacobian射影坐标下3P 运算量减少了1M+ 4S,都有不同程度的效率提高。将提出的Co_Z 点加、3P 运算公式与可抵御SPA攻击的标量乘算法相结合,提出一种Co_Z 对称三进制标量乘算法,使得标量乘算法的运算效率提高了13%。下一步,可选取合适的椭圆曲线,将Co_Z 点加与曲线相结合,提出更高效的标量乘算法,使其能应用到具体的硬件环境中。
| [1] |
MILLER V S. Use of elliptic curves in cryptography [C]// Advances in Cryptology — CRYPTO ' 85 Proceedings. Berlin: Springer-Verlag, 1986: 417-426. https://link.springer.com/chapter/10.1007%2F3-540-39799-X_31
|
| [2] |
KOBLITZ N. Elliptic curve cryptosystems[J]. Mathematics of Computation, 1987, 48: 203-209. DOI:10.1090/S0025-5718-1987-0866109-5 |
| [3] |
LIU H Z, DONG Q H, LI Y B. Efficient ECC scalar multiplication algorithm based on symmetric ternary in wireless sensor networks[C]// 2017 Progress in Electromagnetics Research Symposium. Washington D C: IEEE, 2017: 879-885.DOI: 10.1109/PIERS-FALL.2017.8293258.
|
| [4] |
CHUNG S C, LEE J W, CHANG H C, et al. A high - performance elliptic curve cryptographic processor over GF(p) with SPA resistance[C]// 2012 IEEE International Symposium on Circuits and Systems. Washington D C: IEEE. 2012: 1456-1459.DOI: 10.1109/ISCAS.2012.6271521.
|
| [5] |
FENG X, LI S G. A high-speed and SPA-resistant implementation of ECC point multiplication over GF(p)[C]// 2017 IEEE Trustcom/BigDataSE/ICESS. Washington D C: IEEE, 2017: 255-260.DOI: 10.1109/Trustcom/BigDataSE/ICESS.2017.245
|
| [6] |
MELONI N. New point addition formulae for ECC applications[C]// WAIFI ' 07 Proceedings of the 1st International Workshop on Arithmetic of Finite Fields. Berlin: Springer-Verlag. 2007: 189-201.DOI: 10.1007/978-3-540-73074-3_15.
|
| [7] |
GOUNDAR R R, JOYE M, MIYAJI A. Co -Z addition formulæ and binary ladders on elliptic curves[C]// Cryptographic Hardware and Embedded Systems. Berlin: Springer-Verlag. 2010: 65-79.DOI: 10.1007/978-3-642-15031-9_5
|
| [8] |
WEI J Z, LIU X L, GUO W. A low-time-complexity and secure dualfield scalar multiplication based on Co -Z protected NAF[J]. IEICE Electron Express, 2014, 11(11): 361. DOI:10.1587/elex.11.20140361 |
| [9] |
于伟, 李宝, 王鲲鹏, 等. 特征3有限域上椭圆曲线的Co-Z Montgomery算法[J]. 计算机学报, 2017, 40(5): 1121-1133. YU W, LI B, WANG K P, et al. Co-Z Montgomery algorithm on elliptic curves over finite fields of characteristic three[J]. Chinese Journal of Computers, 2017, 40(5): 1121-1133. (Ch). |
| [10] |
李俊芳, 崔建双. 抗MOV规约法攻击的一类安全椭圆曲线[J]. 计算机工程与应用, 2004(36): 67-68+101. LI J F, CUI J S. A Method to generate elliptic curves[J]. Computer Engineering and Applications, 2004(36): 67-68+101. DOI:10.3321/j.issn:1002-8331.2004.36.021 (Ch). |
| [11] |
HANKERSON D, VANSTONE S MENEZES A. Guide to Elliptic Curve Cryptography[M]. New York: Springer-Verlag, 2004: 72-75.
|
| [12] |
KING B. An improved implementation of elliptic curves over GF(2n) when using projective point arithmetic[C]// Selected Areas in Cryptography. Berlin: Springer-Verlag, 2001: 134-150.DOI: 10.1007/3-540-45537-X_11.
|
| [13] |
LÓPEZ J, DAHAB R. Improved algorithms for elliptic curve arithmetic in GF(2n)[C]// Selected Areas in Cryptography. Berlin: Springer-Verlag, 1998: 201-212.DOI: 10.1007/3-540-48892-8_16.
|
| [14] |
DIMITROV V, IMBERT L, MISHRA P K.. Efficient and secure elliptic curve point multiplication using double-base chains[C]//Advances in Cryptology-ASIACRYPT 2005. Berlin: Springer - Verlag, 2005: 59 - 78.DOI: 10.1007/11593447_4.
|
| [15] |
CIET M, JOYE M, LAUTER K, et al. Trading inversions for multiplications in elliptic curve cryptography[J]. Designs, Codes and Cryptography, 2006, 39(2): 189-206. DOI:10.1007/s10623-005-3299-y |
| [16] |
顾海华.椭圆曲线密码的快速算法及安全基础研究[D].上海: 上海交通大学, 2010. GU H H. Research on Efficient Algorithms and Safety Foundation for Elliptic Curve Cryptosystems[D]. Shanghai: Shanghai Jiao Tong University, 2010 (Ch). http://cdmd.cnki.com.cn/Article/CDMD-10248-2010113593.htm |
| [17] |
邓维勇, 缪祥华. 对称三进制在椭圆曲线标量乘法中的应用[J]. 计算机工程, 2012, 38(5): 152-154. DENG W Y, MIAO X H. Application of balanced ternary in elliptic curve scalar multiplication[J]. Computer Engineering, 2012, 38(5): 152-154. DOI:10.3969/j.issn.1000-3428.2012.05.046 (Ch). |
| [18] |
LIU S G, YAO H T, WANG X A. SPA resistant scalar multiplication based on addition and tripling indistinguishable on elliptic curve cryptosystem[C]// 2015 10th International Conference on P2P, Parallel, Grid, Cloud and Internet Computing (3PGCIC). Washington D C: IEEE, 2015: 785-790.DOI: 10.1109/3PGCIC.2015.20.
|
 2019, Vol. 65
2019, Vol. 65




