文章信息
- 熊盛武, 陈振东, 段鹏飞, 刘晓赟
- XIONG Shengwu, CHEN Zhendong, DUAN Pengfei, LIU Xiaoyun
- 基于可信向量的知识图谱上下文感知表示学习
- Context-Aware Representation Learning of Knowledge Graphs with Credibility Vectors
- 武汉大学学报(理学版), 2019, 65(5): 488-494
- Journal of Wuhan University(Natural Science Edition), 2019, 65(5): 488-494
- http://dx.doi.org/10.14188/j.1671-8836.2019.05.010
-
文章历史
- 收稿日期:2018-09-30

2. 武汉理工大学 交通物联网湖北省重点实验室,湖北 武汉 430070;
3. 武汉理工大学 文法学院,湖北 武汉 430070
2. Hubei Key Laboratory of Transportation Internet of Things, Wuhan University of Technology, Wuhan 430070, Hubei, China;
3. School of Arts and Law, Wuhan University of Technology, Wuhan 430070, Hubei, China
近年来类人智能在世界各地迅猛发展, 其成功离不开完善的知识图谱。通常情况下, 知识图谱中所包含的知识都是以网络和图的架构来组织和表示, 网络和图中的每一个节点表示不同的实体, 每两个节点之间相连的边则表示两个实体之间存在的关系。因此, 传统的知识图谱大多数都是采用〈实体1, 关系, 实体2〉三元组的方式来表示知识, 对应知识图谱中的两个节点以及连接这两个节点的边。
三元组这种表示方法可以很好地表示事实性知识, 但对于模糊知识和复杂形式知识, 例如, 大量涉及人类主观感受、主观情感的知识, 三元组表现能力不足, 当通过传统知识图谱进行知识推理、知识融合的时候, 通常需要研究人员设计特定的图算法来实现, 存在可移植性差、可扩展性差、计算复杂度高以及计算效率低等问题[1], 并且无法有效地挖掘实体间的语义信息。
近年来,以深度学习为代表的表示学习方法引起了很多学者的关注。表示学习旨在将目标对象映射到稠密的低维实值语义空间,在该空间中距离越近其语义关系越紧密。知识表示学习则是对知识图谱中的关系和实体进行表示学习。Bordes等[2]提出了平移模型(translating embeddings,TransE)。对于知识图谱中存在的每一个三元组(h,r,t),TransE模型将关系r看作是头实体h到尾实体t的一个平移,因此TransE模型希望h+r尽可能地靠近t。该模型十分简单,模型的参数较少,模型的计算复杂度较低,但在处理知识图谱中的一对多、多对一以及多对多这种复杂关系时,无法区分在某一方面具有相同语义的实体。
为了对此进行改进,Wang等[3]提出了TransH (translating on hyperplanes)模型。在TransH模型中,作者将头实体向量h和尾实体向量t沿着关系r对应的超平面的法向量wr投影到该超平面上,得到投影后的头实体向量h⊥和尾实体向量t⊥。Lin等[4]提出了TransR(Translating corresponding relation space)模型以及CTransR(cluster-based TransR)模型。在TransR模型中,作者认为应该存在两个不同的向量空间,即实体向量空间和关系向量空间。TransR模型将知识图谱中每一个三元组(h,r,t)的头实体h和尾实体t从实体向量空间中投影到关系向量子空间中。Ji等[5]在TransR模型的基础上提出了TransD模型。对于知识图谱中的每一个三元组(h,r,t),TransD模型为头实体h和尾实体t分别设计了两个不同的投影矩阵Mrh和Mrt,将其投影到对应的关系向量子空间中。
除此之外,类似的还有KG2E[6]和TransG[7]等模型,然而这些算法仅仅利用了知识图谱中的结构化三元组信息进行学习,还有大量的与知识相关的其他非结构化信息没有得到有效利用。
为了提高知识表示学习的区分能力,Tu等[8]加入了文本信息,利用卷积神经网络对网络节点的文本描述信息进行学习,然后将其与网络表示学习融合在一起。段鹏飞等[9]构建了基于空间投影和关系路径的知识表示学习算法,该模型结合空间投影和关系路径来对平移模型进行扩展,并加入关系类型的语义信息进行改进,使复杂关系的建模能力取得了较大的提升。在表示学习中,提升复杂关系表示能力的同时,往往也增加了建模的复杂度。
知识表示贯穿了知识图谱构建与应用的整个过程,设计合理的知识表示方案,更好地涵盖不同类型的知识,是一个重要的研究问题。因此,研究如何高效、准确地表示知识图谱中的知识,有助于提高知识图谱构建质量和水平,对构建知识图谱以及知识图谱的应用具有重大意义。
本文提出了一个基于可信向量和文本信息的知识图谱表示学习模型CKRV (context-aware knowledge representation learning with binary credibility vectors),为每个关系定义一个二值可信向量,不同关系的可信向量关注实体的不同方面。
1 模型描述本文首先给出一些符号的定义。三元组表示为(hi,ri,ti),(i=1, 2, 3, …, nt),hi表示头实体,ti表示尾实体,ri表示关系。实体和关系的向量表示为hi、ri以及ti(i=1,2,3,…,nt),nt表示三元组的总数。
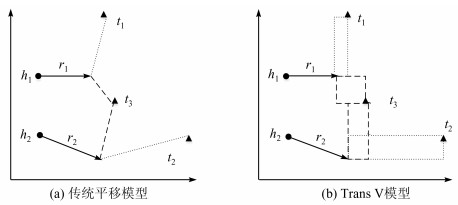
1.1 基于可信度向量的平移模型在TransE模型中,不论是实体向量还是关系向量,向量的每一个维度都被认为是一样重要的,是没有区分度的。例如在图 1(a)中,(h1,r1,t1)和(h2,r2,t2)都是正确三元组,t3是错误的尾实体,由于TransE模型是将每一个维度的距离无差别地进行累加最后得到总距离,所以通过排名算法匹配到了错误的尾实体t3。但如果对实体的每一个维度加以区分,例如在关系r1和关系r2下,x轴维度更为重要,在这种情况下,模型就可以匹配到正确的尾实体t1和t2,如图 1(b)所示。通过对图 1进行分析,我们有理由推测,在不同关系下,同一个实体的不同维度不应该同等对待,只有部分维度会被具体关系影响,而其他维度在该关系下,可以被认定为噪声,如果将每一个维度都无差别地同等对待,将会引入过多的噪声。
|
| 图 1 传统平移模型和TransV模型对比 Fig. 1 Comparison of traditional translation model and TransV model |
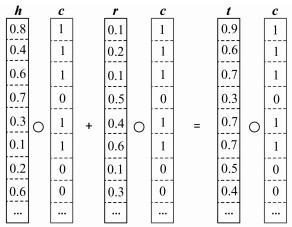
受到TransH、TransR等模型以及上述发现的启发,本文认为:一个实体具有多种不同的属性,不同的语义情景或者关系会与不同的属性或者维度产生相关关系。本文将实体中的每一个维度类比为人类大脑中的一个神经元,不同的神经元组合表示了实体的不同属性信息。在不同的关系r下,实体与关系r相关的属性被激活,无关的属性被抑制,最终使得同一实体在不同关系下具有不同表达。如图 2所示,本文通过一个可信度向量实现此效果,提出基于可信度向量的平移(translating binary credibility vector,TransV)模型。
|
| 图 2 TransV模型的实例 Fig. 2 An example of the TransV model |
在TransV模型中,每个实体和关系都会学习到一个稠密、连续且低维的实值向量表示,实体、关系的语义信息也包含在向量表示中;每一个关系都有一个对应的可信度向量,代表与这个关系对应的实体向量中每个神经元被激活或者被抑制。即给定一个三元组(h,r,t),头实体和尾实体的向量表示为h,t∈ℝn;关系向量表示为r∈ℝn;可信度向量表示为c∈ℝn,c是一个二值向量,其中1代表激活,0代表抑制。n为超参,代表向量空间的维度,本文假定实体和关系向量的维度一样。定义在关系r下被激活的神经元构成的头实体和尾实体的表示为:
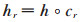
|
(1) |
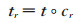
|
(2) |
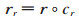
|
(3) |
其中“∘”为哈达玛积(Hadamard product) [10],被激活后的实体和关系拥有类似TransE模型中的平移特性,为此定义TransV的损失函数为:
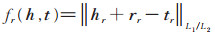
|
(4) |
在对模型进行训练时,本文会对实体h、t和关系r对应的嵌入向量h,t,r进行约束,即∀h,r,t, 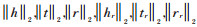
TransV模型需要学习的参数包括头、尾实体向量h、t,关系向量r以及可信度向量c。
1.2 复杂性分析假设整个训练集合中有ne个实体、nr个关系,每个实体的空间向量维度为m,每个关系的向量空间维度为n,那么TransV模型一共有nem+2nrn个参数需要学习。在表 1中,计算了本文的表示学习模型当前需要训练的参数的数量,并与其他流行的表示学习模型可训练参数数量进行了对比。从表 1中可以看出,本文提出的TransV模型需要学习的参数量,与TransE模型和TransH模型需要学习的参数量相差无几,并远远少于TransR模型和TransD模型需要学习的参数量。
| 模型 | 参数数量 |
| TransE | O(nem+nrn),m =n |
| TransH | O(nem+2nrn),m=n |
| TransR | O(nem+nr(m+1)n) |
| CTransR | O(nem+nr(m+d)n) |
| TransD | O(2nem+2nrn) |
| TransV | O(nem+2nrn),m=n |
为了使学习的向量表达充分利用三元组和文本信息,我们使用TransV构建了基于三元组结构信息的向量表示,使用深度卷积神经网络(convolutional neural network,CNN)从实体的文本描述中学习基于上文的向量表示。基于结构的表示方法在描述知识图谱三元组中的结构信息方面做得更好,而基于文本的表示学习在捕获文本语义信息方面效果更好。本文将两种实体表示学习方法融合到相同的连续向量空间中,受TransE模型的启发,将评分函数定义如下:
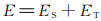
|
(5) |
其中ES是基于结构表示的评分函数,与(4)式相同,ET是基于文本表示的评分函数。为了兼顾原来的训练过程,定义ET如下:
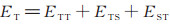
|
(6) |
其中:
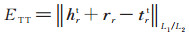
|
(7) |
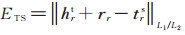
|
(8) |
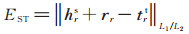
|
(9) |
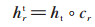
|
(10) |
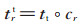
|
(11) |
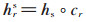
|
(12) |
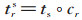
|
(13) |
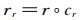
|
(14) |
评分函数ET将两种实体表示学习投影到相同的向量空间中,可以使两种表示学习之间相互影响、相互促进,最终融合在一起,提升实体和关系的向量表示的区分能力。
本文提出使用CNN来构建基于文本的表示。CNN相对于连续词袋模型[11],可以进一步理解文本并利用隐藏在单词顺序中的内部文本信息。
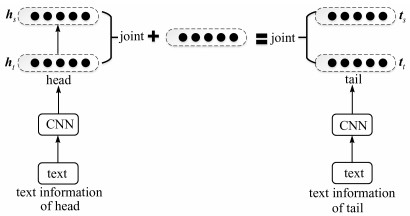
图 3显示了CKRV模型的总体架构。首先,从知识图谱的事实三元组中学习头实体和尾实体的结构化表示。其次,CNN将实体的文本信息作为输入,生成基于文本的实体表示。最后,这些实体表示与二值可信度向量在TransV下联合训练。总体框架构成了CKRV学习模型。
|
| 图 3 CKRV模型整体架构图 Fig. 3 Overall architecture of the CKRV model |
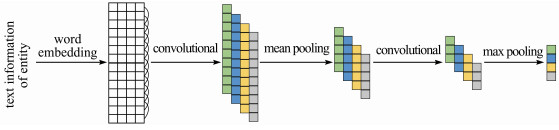
图 4中的CNN架构有5层,在预处理后将某个实体的全文信息作为输入,并输出该实体基于文本的向量表示。通过最小化CKRV的评分函数来训练实体的表示。
|
| 图 4 CNN架构图 Fig. 4 The CNN architecture |
在预处理中,从原始文本中删除所有停用词,单词的词向量作为卷积层输入。在实验中,使用word2vec在维基百科上训练的词向量作为卷积层的输入。其中X(l)为第l层卷积层的输入,滑动窗口的大小为k,输入向量X(l)经过滑动窗口后得到X'(l),定义如下:
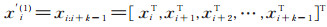
|
(15) |
Z(l)为第l层卷积层的输出,第i个输出向量zi(l)是:
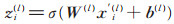
|
(16) |
其中,W(l)∈ℝn2(l)×n1(l)是第l层卷积层的总卷积核,b(l)是第l层卷积层中的偏置。在卷积层之后使用池化层来缩小CNN的参数空间,同时过滤部分噪音。对于第一个池化层,使用最大池化的策略,取区域最大值,能更好保留强特征。选择每个窗口中特征值最大的特征,构建一个新的特征向量xi(2):
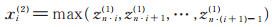
|
(17) |
然而,有一些实体描述的句子十分复杂,还需要关注句子的一些局部特征,只获取该句子中比较明显的特征是不够的,为此,在最后一个池化层,本模型选择使用平均池化替代最大池化,用大小为q,互不重叠的窗口将卷积层的输出向量zi(2)进行分割,然后选择每个窗口中特征值的平均值,构建一个新的特征向量xi(3),
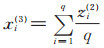
|
(18) |
在模型训练中,需要学习的参数集合为θ=(X,W(1),W(2),E,R,C),其中X表示单词的词向量,E表示实体向量,R表示关系向量,W(1)表示卷积神经网络中第一层卷积层中的卷积核,W(2)表示卷积神经网络中第二层卷积层中的卷积核,C表示每一个关系对应的可信度向量。
卷积神经网络模型的优化使用反向传播的随机梯度下降法,从输出层到第二层平均池化层,再到第二层卷积层,再到第一层最大池化层,再到第一层卷积层,最后到词向量。从后向前依次调整。反向传播的过程中有两种情况下不会调整:1)对于正向传播过程中添加的填充零向量,在反向传播的过程中不会更改;2)对于在池化过程中没有考虑到的部分,如在最大池化层中窗口中的非最大值部分,不会被更新。整个反向传播的链式过程包括从输出层到最初作为输入的词向量,保证了模型的可收敛性质和训练速度[12]。
在训练过程中,采用最大间隔法来提升知识表示的区分能力。为了将正确三元组和错误三元组区分开,需要正确与错误情况下对应损失函数值的差值尽量大,以便区分,让差值尽量增大即为最大间隔法。该方法获取真实三元组和生成三元组的损失函数值后,尽量增加间隔超参的数值,对真伪三元组差值大的奖励,小的则惩罚,使梯度始终朝向差值增加的方向,保证了该模型始终在提升区分能力的优化方向上学习。对于该模型,本文定义目标函数为:
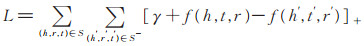
|
(19) |
其中,[x]+=max (0,x),表示返回0和x之间的较大的那个值;γ > 0为间隔超参,代表正确三元组损失函数值与错误三元组损失函数值之间的间隔距离。f(h,t,r)为损失函数,S为正确三元组的集合,S-为错误三元组集合。为构造更多的负样本,本文将一个正确三元组中的头实体、尾实体或者关系替换,构成一个错误三元组。使用随机梯度下降法更新hs,ts,ht,tt,W(1),W(2)和嵌入单词X。
同时本文使用类似于蚁群算法中的信息素的方法更新c,每一个可信度向量有一个对应的信息素向量p。p中某一维度信息素越大则代表越多的蚂蚁愿意访问该维度,而信息素随着蚂蚁的增多而保持更久,因此形成正反馈。最优维度上的信息量越来越大,其他维度上的信息素会随着时间不断减小。同理与关系相关的属性激活概率变大,而无关属性被激活概率变小,因此在对应关系中与实体相关的属性会对评分函数影响更大。在一个批尺度下所有蚂蚁完成一次遍历后,对残留的信息素,各个维度上的信息素按照下式进行调整,
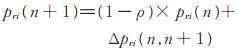
|
(20) |
其中,pri表示的是关系r对应的信息素向量pr的第i个维度;ρ是挥发率,取值在0~1之间。pri(n)为第n次迭代后r对应信息素的值,Δpri(n,n+1)是n到n+1次迭代过程中i维度信息素累积的值,并且本文限制信息素的值在0~1之间。本文根据关系r对应的信息素向量pr生成对应的可信度向量c。
3 数值实验 3.1 数据集与实验设置本文采用FB15K来评估TransV和CKRV模型预测的准确性。FB15K是典型大规模知识图谱Freebase的一个子集。FB15K中包含14 951个实体,1 345条关系,483 142个训练三元组,59 071个测试三元组。本文参考文献[12]方法,从FB15K中的14 951个实体中剔除了47个实体,这47个实体的实体描述的单词个数小于3或者没有描述词,并将相关的三元组从训练集、测试集以及验证集中剔除,这样就构成了一个新的数据集——FB15K(filter)。表 2列出了数据集的统计数据。
| Dataset | #Rel | #Ent | #Train | #Valid | #Test |
| FB15K(raw) | 1 345 | 14 951 | 483 142 | 5 000 | 59 071 |
| FB15K(filter) | 1 345 | 14 904 | 472 860 | 48 991 | 57 803 |
本文训练过程中的超参包括实体和关系向量的维度m,n,学习率α,间隔γ,批大小batch,其中:

|
通过实验获取TransV的最佳配置是:m=n=200,γ=3,α=0.001,batch大小为300,迭代次数为3 000次。
3.2 实体预测本文将TransE模型中通过随机替换正确三元组的头实体或者尾实体来构造错误三元组,这种构造负样本的方法称为“unif”;将TransH模型中根据关系的类型不同设置不同的概率来替换头实体或者尾实体来构造错误三元组,这种构造负样本的方法称为“bern”,“bern”采样技巧对比“unif”可以减少假阴性标签[3]。
实体预测采用两种评估指标:1)正确预测实体的平均打分;2)实体排名前10位的有效实体比例(Hits@ 10)。TransV对FB15K的实验结果如表 3所示。
| Metric | Mean Rank | Hits@10/% | |||
| Raw | Filter | Raw | Filter | ||
| TransE[2] | 243 | 125 | 34.9 | 47.1 | |
| TransH(unif)[3] | 211 | 84 | 42.5 | 58.5 | |
| TransH(bern)[3] | 212 | 87 | 45.7 | 64.4 | |
| TransR(unif)[4] | 226 | 78 | 43.8 | 65.5 | |
| TransR(bern)4 | 198 | 77 | 48.2 | 68.7 | |
| CTransR(unif)[4] | 233 | 82 | 44.0 | 66.3 | |
| CTransR(bern)[4] | 199 | 75 | 48.4 | 70.2 | |
| TransD(unif)[5] | 211 | 67 | 49.4 | 74.2 | |
| TransD(bern)[5] | 194 | 91 | 53.4 | 77.3 | |
| TransV(unif) | 196 | 53 | 50.0 | 74.4 | |
| TransV(bern) | 182 | 81 | 52.2 | 73.1 | |
由表 3可见:1)在相同的负样本构造方式下, TransV优于TransE、TransH和TransR等模型;2)在相同的负样本构造方式下, TransD在Hits@10上比TransV表现更好,但是TransD比TransV更复杂(如表 1所示);3) “bern”采样技巧下的排名比“unif”的更靠前,前10占比也更大。
表 4统计了不同模型在不同关系类型下预测实体的排名在前10的百分比,并细分为两种不同情况:预测头实体和预测尾实体。从表 4中我们可以看出TransV在“unif”和“bern”采样技巧的数据集中都显著优于TransE,TransH和TransR。与TransV相比,TransD在一对一(1-1)和多对多(N-N)关系中表现更好。考虑到模型的性能和复杂性,TransV更适用于知识图谱的建模。
| % | |||||||||
| Metric | Prediction Head(Hits@10) | Prediction Tail(Hits@10) | |||||||
| 1-1 | 1-N | N-1 | N-N | 1-1 | 1-N | N-1 | N-N | ||
| TransE[2] | 43.7 | 65.7 | 18.2 | 47.2 | 43.7 | 19.7 | 66.7 | 50.0 | |
| TransH(unif)[3] | 66.7 | 81.7 | 30.2 | 57.4 | 63.7 | 30.1 | 83.2 | 67.2 | |
| TransH(bern)[3] | 66.8 | 87.6 | 28.7 | 64.5 | 65.5 | 39.8 | 83.3 | 67.2 | |
| TransR(unif)[4] | 76.9 | 77.9 | 38.1 | 66.9 | 76.2 | 38.4 | 76.2 | 69.1 | |
| TransR(bern)[4] | 78.8 | 89.2 | 34.1 | 69.2 | 79.2 | 37.4 | 90.4 | 72.1 | |
| CTransR(unif)[4] | 78.6 | 77.8 | 36.4 | 68.0 | 77.4 | 37.8 | 78.0 | 70.3 | |
| CTransR(bern)[4] | 81.5 | 89.0 | 34.7 | 71.2 | 80.8 | 38.6 | 90.1 | 73.8 | |
| TransD(unif)[5] | 80.7 | 85.8 | 47.1 | 75.6 | 80.0 | 54.5 | 80.7 | 77.9 | |
| TransD(bern)[5] | 86.1 | 95.5 | 39.8 | 78.5 | 85.4 | 50.6 | 94.4 | 81.2 | |
| TransV(unif) | 78.0 | 90.1 | 48.9 | 74.6 | 76.8 | 77.2 | 57.3 | 87.5 | |
| TransV(bern) | 79.0 | 95.6 | 37.2 | 73.0 | 77.7 | 47.3 | 94.6 | 76.5 | |
CKRV与TransV的实体预测对比如表 5所示(m=n=100,α=0.001,γ=1.0),从中我们可以看出,在相同的实体和关系向量维度、间隔和学习率情况下,融合了文本信息的CKRV在实体预测实验中,其平均排名靠前同时排名在前10所占比例较高,可以提高TransV的性能。
| Metric | Mean rank | Hits@10/% | |||
| Raw | Filter | Raw | Filter | ||
| TransV | 219.296 | 133.727 | 41.128 | 53.264 | |
| CKRV | 211.155 | 124.748 | 43.572 | 56.892 | |
本文提出了TransV和CKRV模型用于知识图谱的表示学习,使用深度卷积神经网络来提取实体文本信息的语义。在实验中,评估了实体预测的模型。实验结果表明,TransV模型比TransE、TransH和TransR具有更好的性能,TransD在某些方面表现优于TransV,但TransD比TransV更复杂,CKRV可以提高TransV的性能。
未来可从以下两个方向展开研究:1)在CKRV模型添加其他的信息,如图像信息,更进一步地提升模型的区分能力;2)设计一种更完善高效的方法来提取CKRV模型中的文本信息。
| [1] |
刘知远, 孙茂松, 林衍凯, 等. 知识表示学习研究进展[J]. 计算机研究与发展, 2016, 53(2): 247-261. LIU Z Y, SUN M S, LIN Y K, et al. Knowledge representation learning:A review[J]. Journal of Computer Research and Development, 2016, 53(2): 247-261. DOI:10.7544/issn1000-1239.2016.20160020 (Ch). |
| [2] |
BORDES A, USUNIER N, GARCIA-DURAN A, et al. Translating embeddings for modeling multi-relational data [C]// Advances in Neural Information Processing Systems. Nevada: MIT Press, 2013, 2787-2795.
|
| [3] |
WANG Z, ZHANG J W, FENG J, et al. Knowledge graph embedding by translating on hyperplanes[C]// AAAI' 14 Proceedings of the 28th AAAI Conference on Artificial Intelligence. Menlo Park: AAAI Press, 2014: 1112-1119.
|
| [4] |
LIN Y K, LIU Z Y, SUN M S, et al. Learning entity and relation embeddings for knowledge graph completion[C]// AAAI' 15 Proceedings of the 29th AAAI Conference on Artificial Intelligence. Menlo Park: AAAI press, 2015: 2181-2187.
|
| [5] |
JI G C, HE S Z, XU L H, et al. Knowledge graph embedding via dynamic mapping matrix[C]// Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing(Volume 1: Long Papers). New York: The Association for Computational Linguistics, 2015: 687-696. DOI: 10.3115/v1/p15-1067.
|
| [6] |
HE S Z, LIU K, JI G L, et al. Learning to represent knowledge graphs with gaussian embedding[C]// ACM International on Conference on Information and Knowledge Management. New York: ACM Press, 2015: 623-632. DOI: 10.1145/2806416.2806502.
|
| [7] |
XIAO H, HUANG M L, ZHU X Y. TransG: A generative model for knowledge graph embedding[C]// Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers). Berlin: Association for Computational Linguistics, 2016: 2316-2325. DOI: 10.18653/v1/p16-1219.
|
| [8] |
TU C C, LIU H, LIU Z Y, et al. Cane: Context-aware network embedding for relation modeling[C]// Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics(Volume 1: Long Papers). Stroudsburg: Association for Computational Linguistics, 2017: 1722-1731. DOI: 10.18653/v1/p17-1158.
|
| [9] |
段鹏飞, 王远, 熊盛武, 等. 基于空间投影和关系路径的地理知识图谱表示学习[J]. 中文信息学报, 2018, 32(3): 26-33. DUAN P F, WANG Y, XIONG S W, et al. Space projection and relation path based representation learning for construction of geography knowledge graph[J]. Journal of Chinese Information Processing, 2018, 32(3): 26-33. DOI:10.3969/j.issn.1003-0077.2018.03.004 (Ch). |
| [10] |
MILLION E. The hadamard product[J]. Course Notes, 2007, 3(1): 1-6. |
| [11] |
MANNING C D, RAGHAVAN P, HINRICH SCHÜTZE. Introduction to Information Retrieval[M]. Cambridge: Cambridge University Press, 2008: 117-119.
|
| [12] |
XIE R B, LIU Z Y, JIA J, et al. Representation learning of knowledge graphs with entity descriptions[C]// 30th AAAI Conference on Artificial Intelligence. Menlo Park: AAAI Press, 2016: 2659-2665.
|
 2019, Vol. 65
2019, Vol. 65





